黑胡椒颗粒的介电特性混合方程研究

王品正， 李 锋， 张汝怡， 朱亚莉， 李 双， 焦 阳*，3，4

（1. 国家淡水水产品加工技术研发分中心（上海） / 上海海洋大学 食品学院，上海201306；2. 上海海洋大学 食品热加工工程技术研究中心，上海201306；3. 南京工业大学 食品与轻工学院，江苏 南京211816；4. 天顺农副产品有限公司，江苏 徐州221000）

黑胡椒（Piper nigrum）是胡椒科的一种开花藤本植物，晒干后的果实常作为香料和调味品使用[1]，由于其独特的风味、色泽和香气，一直受到人们的喜爱，是世界上消费最广泛的香料之一。 然而，黑胡椒在收获、 贮藏及加工过程中可能受到交叉污染，导致其病原菌及菌落总数过高，因此往往需对收获或贮藏后的黑胡椒进行杀菌处理，从而提高其作为配料添加至其他食品中的安全性。 目前，黑胡椒在工业生产中主要的杀菌方式为蒸汽杀菌， 耗能较高，且须后续干燥去除多余的水分，过程复杂且高温对黑胡椒的品质有显著影响，因此，亟待研发新型杀菌技术。

射频杀菌是一种新型热杀菌技术，通过高频电磁波使物料内部分子剧烈震动摩擦，实现快速整体加热，使物料中的目标菌达到热致死[2]。 射频杀菌快速便捷，对物料的品质影响较小，具有较为广阔的应用前景。 计算机仿真在辅助开发杀菌工艺中能够节省大量的人力、物力、财力及时间成本，避免了大量重复试验，其在射频加热过程中的模拟已被验证具有有效性且模拟结果真实可靠。 Wang 等[3]以小麦粉作为低水分食品的代表， 采用有限元软件FEMLAB®开发了12 kW，27.12 MHz 平行板射频系统的计算机模型。 仿真结果表明，射频功率密度分布的不均匀在一定程度上导致样品温度的不均匀，且试验结果和模拟结果有较好的一致性。 Li 等[4]使用有限元软件COMSOL Multiphysics®辅助研究射频加热不同形状和尺寸牛肉的温度均匀性情况时，根据牛肉在特定温度范围内的介电特性及热特性所建立的数值模型能准确预测不同形状和尺寸的牛肉样品在射频解冻过程中的温度分布情况。

射频加热中，物料的介电特性决定了食品和电磁能之间的相互作用，也是影响射频加热速率及均匀性的关键因素。 介电特性主要用介电常数与介电损耗来表示[4]，表述为：

式中：ε*为复介电特性，（F/m）；ε′为介电常数，（F/m）；j 为虚数单位；ε″为介电损耗，（F/m）。

食品样品的介电特性测量一般采用开放式同轴探头与网络分析仪连接，使样品表面与探头平面充分贴合后测定。 颗粒状样品不具备平整表面，如将样品磨粉后进行测量，介电特性则会受密度变化的影响[5-6]。 因此，有研究将颗粒制成粉末并压缩测得介电特性，并通过几种混合方程开发出一系列混合物的介电特性模型来预测颗粒状样品的介电特性[7-9]。施火结等[10]将脱脂奶粉作为研究对象，将奶粉压缩为块状测其介电特性， 并用CRIME、LLLE、LE和BE 混合方程回归计算得到未压缩脱脂奶粉的介电特性， 再通过COMSOL 仿真模拟与试验对比得出，LE 方程获得的介电特性与实际更吻合。目前，国内外尚未有关于黑胡椒颗粒介电特性的研究。

作者以黑胡椒颗粒为对象，将颗粒制粉后的密度压缩到与颗粒密度一致， 测得压制后的介电特性，通过常用的3种介电特性混合方程计算得到黑胡椒颗粒的介电特性，并运用计算机有限元模拟及射频加热试验验证混合方程的有效性。

1 物料特性测量与混合方程

1.1 材料与仪器

1.1.1 材料黑胡椒颗粒：上海味好美食品有限公司提供；黑胡椒初始含水率（9.76±0.15）%，水分活度（0.673±0.023）。

1.1.2 仪器介电特性测试系统 （E5071C 矢量网络分析仪及85070B 末端开路的同轴探头）：美国安捷伦科技有限公司产品；电子天平YP802N：上海天美天平仪器有限公司产品； 食品粉碎机JS66D-300型： 苏泊尔股份有限公司产品； 温度监测系统（LR8401-21 数据记录仪）：日置（上海）商贸有限公司产品；KD2 PRO 热导率测试仪： 美国Decagon 公司产品；FLIR A655 红外热像仪：美国FLIR 公司产品；TA Q2000 差示扫描量热仪：美国TA Instruments公司产品；Labotron12 射频加热系统： 法国Sairem公司产品。

1.2 方法

1.2.1 介电特性的测量将磨粉后的黑胡椒密度压缩至与其颗粒密度一致，并放置于圆柱状金属容器（H：10 cm D：2.1 cm）中，顶端部分放置少量胡椒粉以保证探头与物料的充分接触，然后通过开放式同轴探头及网络矢量分析仪测得压缩后样品的介电特性[8]。

1.2.2 导热系数的测量将装满黑胡椒颗粒 （约964 g） 的聚丙烯容器放置在恒温箱中， 并将KD2 PRO 的测量探针固定在容器中心，以10 ℃为测量间隔， 在目标温度下保持20 min 测量其在20～100 ℃下的导热系数。

1.2.3 比热容的测量称取黑胡椒粉末（20±0.06）mg，测量温度：10～120 ℃，升温速率：1 ℃/min，采用DSC 三步法（测基线、标样和样品）测量黑胡椒的比热容[11]。

1.2.4 数据统计分析所有数据利用Microsoft Excel 2010 进行统计和分析处理，用Origin 2017 进行作图， 电压方程采用MATLAB R2016a 进行编程计算。

1.3 介电特性的混合方程

混合方程通常用于计算不同介质混合物的介电特性，通过预实验选择以下3个混合方程作为研究对象[12]：

CRIME 方程（Complex Refractive Index mixture equation）

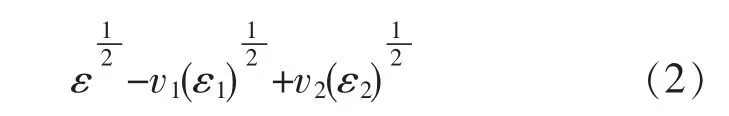
LLLE 方 程 （Landau and Lifshitz，Looyenga equation）

BE 方程（Bottcher equation）

式中：ε 为颗粒的介电特性；ε1为空气的介电特性；ε2为压缩粉末的介电特性；v1和v2分别表示自然堆积下空气和颗粒的体积占比，v1+v2=1；v1等于自然堆积下颗粒间的孔隙率e。 孔隙率的计算公式为：

式 中：ρa为 堆 积 颗 粒 的 密 度，（kg/m3）；ρs为 压 缩粉 末的密度[12]，（kg/m3）。

2 有限元模拟及实验验证

2.1 理论依据

黑胡椒的射频加热过程是一个多物理场耦合过程，主要包括电磁场和热传递两个物理场。

2.1.1 电磁场理论电磁场中的电场强度一般通过麦克斯韦电磁场方程求解。 在27.12 MHz 射频系统中，麦克斯韦方程可转化为准静态法假设的拉普拉斯方程计算：

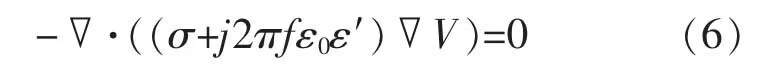
式中：▽为散度算符；σ 为物料的电导率，（S/m），j=（-1）0.5；f 为频率 （Hz）；ε0为真空介电常数；ε′为物料的相对介电常数；V 为两极板间电压，（V）[13]。

2.1.2 热传导理论射频加热过程中，物料内部的传热由傅立叶方程描述：

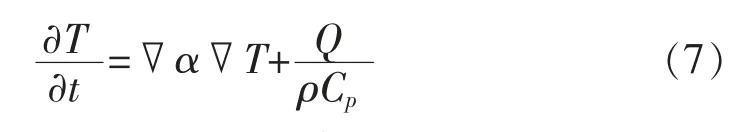
式中：∂T/∂t 为物料的升温速率，（℃/s）；α 为热扩散系 数，（m2/s）；ρ 为 密 度，（kg/m3）；Cp为 比 热 容，（J/（kg·K））；Q 为单位体积物料所吸收的电磁能，（W/m3），由公式（8）表述：

式中：ε″为物料的相对介电损耗；E 为电场强度，（V/m），E=-▽V[3]。

2.1.3 初始值和边界条件射频加热过程中，物料外部与空气有对流换热，可用牛顿定律式表示：

式中：h 为对流换热系数，（W/(m2·K)）；Tair为射频腔内的空气温度，（℃）[14]。

射频系统运行过程中，高频高压电场中难以测定极板电压， 因此采用公式推导法预测极板电压[15-17]：

式中：dair为上极板到物料上表面的距离，（m）；dmat为物料高度，（m）[18]。

射频加热过程中电压不断变化，而在模拟加热过程中， 电压的大小直接影响着加热速率的快慢。而根据电压推导公式（10）可以看出，物料的升温速率也是影响电压大小的变量之一。 作者通过公式推导法推算电压，选择实际加热过程中中心点的升温速率作为模拟过程中电压公式中的参数，根据公式（10），得到电压值，结合试验结果，确定最终的模拟电压值。

2.2 模型建立

采用COMSOL Multiphysics（v5.2）软件建立电磁场-热传递双向耦合模型求解。 运行软件的服务器配置为： 戴尔处理器， 双Intel Xeon CPU 2.60 GHz， 运 行 内 存128 GB，Windows Sever 2012 R2 Standard 64 位操作系统。

射频系统加热腔及物料尺寸见图1， 物料的尺寸与实验中盛放黑胡椒的聚丙烯容器大小一致（单位：cm），上下极板间距为9 cm，物料放置在下极板正中心位置[19]。 模拟加热过程中初始条件的参数设置如表1。

采用自由剖分四面体网格设置模型中的全部域，COMSOL 5.2 软件中网格划分精细程度共有9个级别，分别为极端细化、特别细化、较细化、细化、标准、粗化、较粗化、特别粗化和极端粗化。 有限元模拟中，极端细化和特别细化两种级别的网格划分得到的结果非常接近，但极端细化的时间约是特别细化的3 倍。 因此，物料网格选择“特别细化”，同时为了减少计算机的计算量，缩短计算时间，将周围空气的网格划分设为细化级别。

图1 射频加热腔及物料尺寸Fig. 1 Chamberfor radio frequency heating and thematerial size

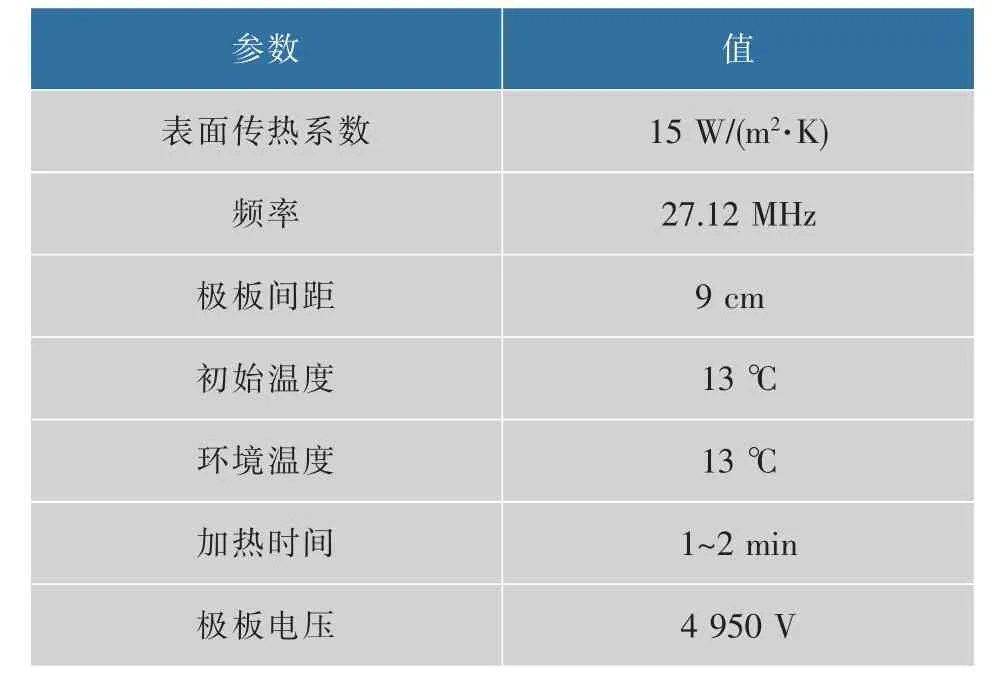
表1 模型初始和边界条件Table 1 Initial and boundary conditions of the model

2.3 实验验证

射频加热系统由射频发生器，包含有可调间距的上下两平行电极板加热腔和光纤测温系统组成。黑胡椒样品（约960 g）放入聚丙烯容器装满，物料中间层用纱布隔开，便于使用红外热像仪观测中间层截面温度分布。 将2 条光纤传感器插入容器几何中心和距角1.5 cm 深处固定，通过测温系统实时监测升温曲线，组合系统的示意图见图2[13]。 试验过程中，加热1.0、1.5、2.0 min，结束后将物料立即取出置于红外热像照相机下进行中间层温度采集，确定冷热点温度及总体温度分布情况。 有限元模拟与试验的初始及试验条件保持一致。

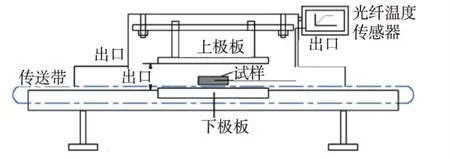
图2 27.12 MHz、12 kW 平行极板式射频加热系统示意Fig. 2 Schematic diagram of a 27.12 MHz，12 kW parallel plate systemfor radio frequency heating

3 结果与分析

3.1 黑胡椒的介电特性及热特性

实验测得黑胡椒粉末密度为0.641 kg/m3，堆积颗粒密度为0.578 kg/m3，颗粒密度为1.15 kg/m3，将测量结果代入 （5） 式中， 得到堆积颗粒孔隙率=0.641。 测得压缩后的介电特性并代入混合方程，通过MATLAB 软件对方程求解，计算得到的介电特性如表2。 实际测得黑胡椒颗粒比热容和导热系数随温度变化如表3。

根据数值模拟与试验结果对比，确定了最终可用的介电混合方程为CRIME 方程， 将黑胡椒颗粒的热物理特性和介电特性拟合成方程，拟合程度较好（R2>0.9），如表4 所示。

3.2 黑胡椒射频加热过程模拟及实验结果分析

3.2.1 加热过程中电压射频加热过程中，实际电压为变化值，在不扰动电场前提下，很难测得实际电压值[20]。 目前，一些关于射频加热模拟的研究中，模拟电压均采用了固定值[13，15，21]。 而Uyar 等[22]在研究牛肉射频解冻的模拟中，通过试错法对电压推导值进行改进，其模拟结果与试验基本相符。 据此，运用公式推导出电压值，再降低一定比例可得到实际电压。 作者通过公式推导出电压值并不断试错，确定模拟电压为4950 V。

表2 黑胡椒粉末压缩后在27.12 MHz 下的介电特性及混合方程计算值Table 2 Dielectric properties of black pepper powder after compression and calculated values of mixing equation at 27.12 MHz

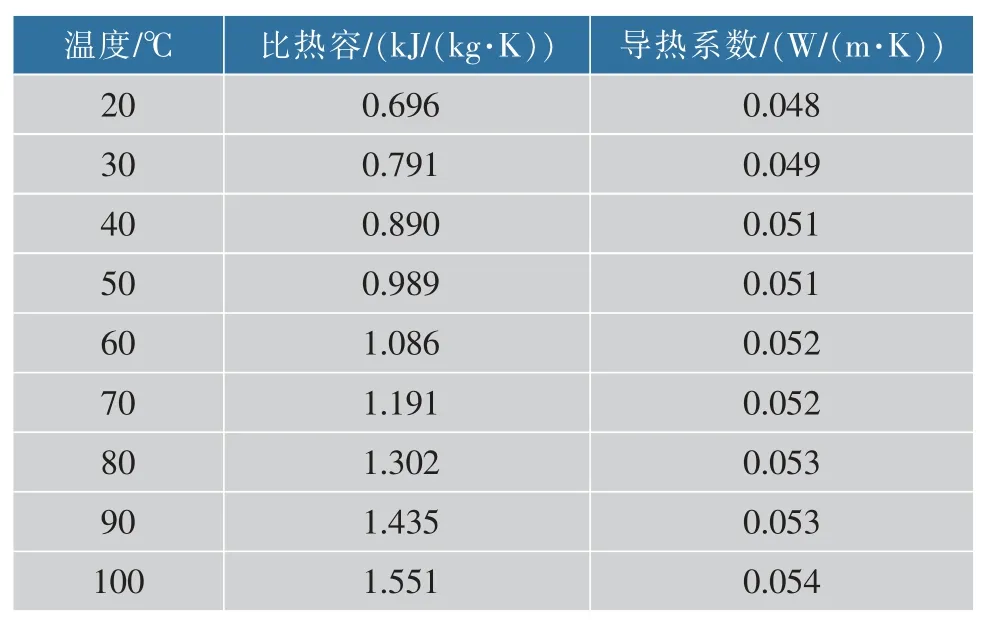
表3 黑胡椒颗粒的比热容和导热系数Table 3 Specific heat capacity and thermal conductivity of black pepper particles

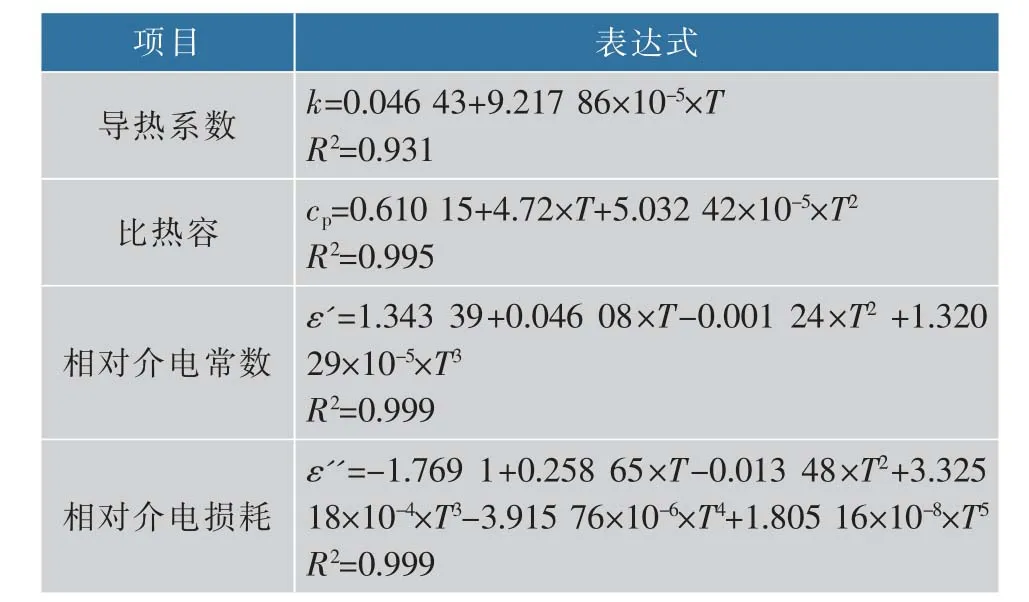
表4 黑胡椒物性参数Table 4 Black pepper physical parameters.

3.2.2 升温曲线对比分析由图3 和图4 可以看出，CRIME 方程得到的模拟结果与试验值更为接近。 加热0～1 min 时，中心点处试验值温度较低，而1～2 min 时二者中心点升温趋势趋于一致。LLLE 和BE 方程模拟的仿真结果显示，与试验值相比，中心点温差分别为27.7、25.6 ℃， 边角点ΔT 分别为52.7、50.1 ℃，有较大差异。 此外，对比图3、图4 发现， 试验值的边角温度比中心温度的误差值要大。实际加热中，物料为黑胡椒颗粒堆积的不规则形状物料，并且射频加热存在边角效应，导致了黑胡椒整体边角处温度的误差较高。

图3 模拟与试验射频加热中心点温度变化Fig. 3 Temperatures of simulation and experiment center pointsover time during radio frequency heating

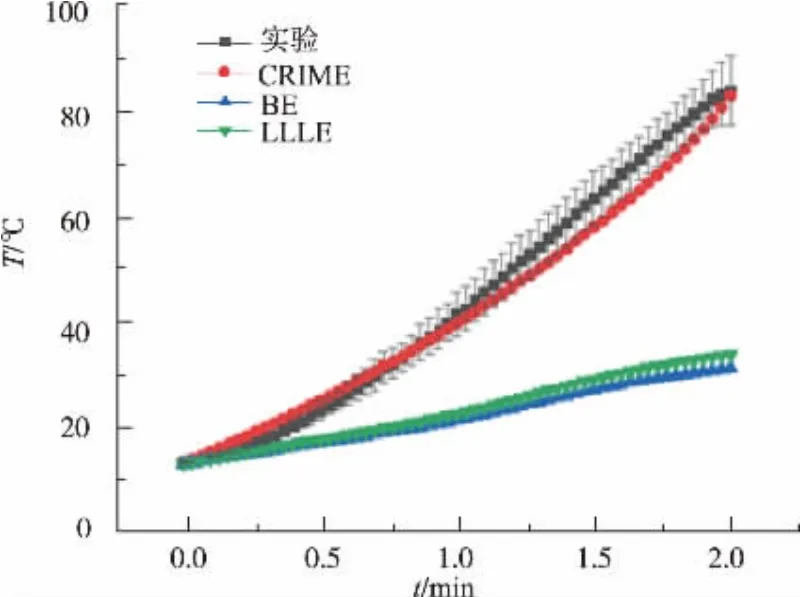
图4 模拟与试验射频加热边角点温度变化Fig. 4 Temperatures of simulation and experiment corner pointsover time during radio frequency heating

3.2.3 温度分布对比分析从图5-7 中可以看出，加热过程中均存在一定程度的边角效应，当时间延长至2 min，边角效应更加明显。CRIME 方程模拟2 min 时的温度与试验值差别最大，如图7（b），边角最高温度达到了215 ℃，明显高于试验值。 这可能是样品热物理特性的测量有一定误差，而计算机模拟过程中放大了热逃逸的现象，导致边角温度过高[24]。而由CRIME 方程对应的中间层热型图可以看出，虽然存在边角过热现象，但是过热部分面积很小，相对于整个截面来看，可以忽略不计。 总的来说，CRIME 方程和试验两种方式得到物料的整体温度分布较一致，加热1.0、1.5、2.0 min 时，大部分中间层区域的温度分别在34、52、68 ℃左右。 根据CRIME 方程计算得到的黑胡椒颗粒介电特性，在27.12 MHz，20～90 ℃条 件 下 由1.89-0.11j 增 加 到5.11-4.43j，因此在0～2 min 射频加热过程中，物料内部热偏移加剧。 除了边缘处极小部分区域存在过热效应， 从图6-8 中的试验值与CRIME 方程的仿真结果来看， 试验值与CRIME 方程对应的模拟结果中大部分区域的温度分布有较好的一致性。 结果表明， 运用CRIME 方程模拟出的温度分布与实际最为接近， 证明了CRIME 方程用于推导黑胡椒颗粒介电特性的有效性。

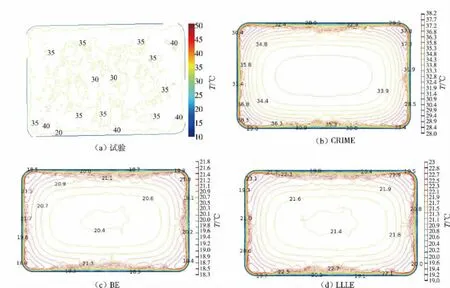
图5 黑胡椒射频加热1 min 时试验和介电混合方程模拟的中间层温度分布图Fig. 5 Intermediate layer temperature in the experiment and simulation of dielectric mixed equation of black pepper at 1 min of radio frequency heating

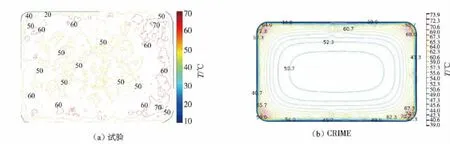
图6 黑胡椒射频加热1.5 min 时试验和介电混合方程模拟的中间层温度分布图Fig. 6 Intermediate layer temperature in the experiment and simulation of dielectric mixed equation of black pepper at 1.5 min of radio frequency heating

图7 黑胡椒射频加热2 min 时试验和介电混合方程模拟的中间层温度分布图Fig. 7 Intermediate layer temperature in the experiment and simulation of dielectric mixed equation of black pepper at 2 min of radio frequency heating

综上，CRIME 方程模拟得到的结果与试验值更匹配， 即CRIME 推导出黑胡椒的介电特性更接近实际值。Liu 等[12]使用介电混合方程的方法研究了面包的介电特性， 研究发现由LE 方程计算出的介电常数和由LLLE 计算出的介电损耗所得到的仿真结果与实际更符合。

4 结 语

测量了黑胡椒粉随温度变化的介电特性及热特性参数并运用介电特性混合方程推导获得黑胡椒颗粒的介电特性，通过建立黑胡椒加热过程的有限元模型验证运用方程获取黑胡椒介电特性参数的准确性。 证明了通过混合方程推导出农产品中颗粒状物料介电特性具有可行性，建立的数值模型可用于颗粒物料加热的均匀性研究，确定最佳加热及杀菌工艺，节省实验所需财力和人力。