基于反向传播人工神经网络的酱牛肉中金黄色葡萄球菌的生长模型
2020-09-10范志文光翠娥干建平
范志文, 光翠娥*, 干建平
(1. 食品科学与技术国家重点实验室,江南大学,江苏 无锡214122;2. 黄冈师范学院 经济林木种质改良与资源综合利用湖北省重点实验室/大别山特色资源开发湖北省协同创新中心,湖北 黄冈438000)
酱牛肉是我国历史悠久的佳肴, 因色泽鲜嫩、味道鲜美,营养价值高而深受人们喜爱。 酱牛肉的制作大多采用传统手工制作, 导致酱牛肉在生产、加工、运输、销售过程中极易被食源性病原菌污染,从而引发食品安全问题,给消费者的健康带来不可估量的安全隐患。 金黄色葡萄球菌广泛存在于自然界中,是造成细菌性食物中毒的主要原因,极易造成食品污染[1]。 曹军等[2]人对无锡市场的酱卤肉进行监测,1186 件熟制品中有61 件检出金黄色葡萄球菌,检出率高达5.14%;许振伟等[3]人对上海市场所监测的396 份散装熟食肉制品进行金黄色葡萄球菌及肠毒素分析,样品中金黄色葡萄球菌阳性数70份检出率为17.70%;2015年在三门峡市监测的60份网店食品中,30 份自制熟肉中金黄色葡萄球菌3份,检出率为10.00%[4]。由此可见酱卤肉制品中金黄色葡萄球菌的污染比较严重。
预测微生物学是运用微生物学、数学、统计学及计算机学建立数学模型,用数学语言预测和描述食源性微生物在特定环境条件下的生长和死亡规律的学科[5-6]。由Whiting 等[7]提出的基于变量类型的分类方法将预测微生物数学模型分为一级模型、二级模型和三级模型,其中一级模型描述了微生物数量与时间的函数关系。在众多初级模型中,Gompertz方程能有效描述微生物生长,在腐败细菌生长动力学研究中被广泛使用[8-11]。但由于模型中的参数是凭经验建立并无实际意义,使得模型在复杂的环境因子中很难确切地进行预测[12-13]。
人工神经网络是模拟大脑神经网络的结构和功能,将多个处理单元相互连接,进行自组织、自适应、自学习,从而模拟人类的学习、认知、智能的过程[14]。 误差反向传播神经网络是一种单向传播的多层前馈网络,它采用典型的有教师学习方式来进行预测和分类问题的处理。 一个训练好的反向传播神经网络,能够逼近任何自变量和因变量之间的函数关系[15]。 不需要考虑自变量是否满足正态性及变量间独立等条件, 可识别变量间复杂的非线性关系,尤其是用现有统计方法无法达到目的或效果不好时,采用此模型往往收到很好的效果[16-17]。 作者将预测微生物学应用到酱牛肉制品中,利用人工神经网络建立模型, 揭示金黄色葡萄球菌的生长变化规律, 为酱牛肉中的金黄色葡萄球菌控制提供依据,从而降低食源性疾病发生的可能性。
1 材料与方法
1.1 菌种与材料
金黄色葡萄球菌:(CMCC26003): 北纳创联生物技术有限公司产品; 酱牛肉: 市售;Baird-Parker平板、亚碲酸钾卵黄菌增液:上海谷研实业有限公司产品。
1.2 仪器与设备
CHP-80 培养箱: 上海市三发科学仪器有限公司产品;DSX-280B 手提式压力蒸汽灭菌器:上海申安医疗器械厂产品;GZX-9070 MBE 电热鼓风干燥箱:上海博讯实业有限公司医疗设备厂产品;SF-CJ-1A净化工作台:上海三发科学仪器有限公司产品。
1.3 实验方法
1.3.1 菌种的活化和酱牛肉的预处理在无菌条件下将于4 ℃冷藏的冻干菌粉去除标签,用体积分数75%乙醇擦拭管壁,将0.3 mL 左右无菌水注入冻干管中,吹打,充分溶解成菌悬液。取0.2 mL 菌悬液加入50 mL 的灭菌营养肉汤在36 ℃下培养48 h,然后进行平板划线分离置于36 ℃培养箱中培养,传代2次。
酱牛肉的预处理:将酱牛肉除去筋骨,分割成约1 cm3的小块,置于培养皿中,每份10 g,灭菌,用无菌封口膜密封培养皿贮藏待用。
1.3.2 不同温度下生长曲线的测定挑取一环金黄色葡萄球菌菌落,浸入装有10 mL 灭菌生理盐水试管中振荡, 制成浓度为107~108CFU/mL 的菌悬液。 用生理盐水稀释菌悬液,制成染菌浓度分别为102、103、104CFU/mL 的菌悬液, 取不同接种浓度的菌液1 mL 匀喷洒在处理好的酱牛肉中, 分别置于15、25、36 ℃下培养。 其中36 ℃下2 h 取样测量一次,25 ℃下3 h 取样一次,15 ℃下12 h 取样一次。每次10 g 样品置于装有90 mL 无菌生理盐水的锥形瓶中振荡,依次进行10 倍稀释。 选取2个稀释度适宜的样品, 每次吸取2个100 μL 样品加入Baird-Parker 平板中,用涂布棒涂布[18]。 倒置于36 ℃培养箱中培养24~48 h。
1.3.3 反向传播神经网络的建立反向传播神经网络是一种基于在误差面上寻找最小误差原理设计的算法,它通过激活函数产生输出信号,据定义的损失函数计算真实值和预测值之间的误差来进行权值的修正[19]。 第一层为输入层,含有3个神经元,分别代表温度、接菌量及保存时间;第二层为隐含层, 用于处理输入信息与输出结果的非线性关系;第三层为输出层,含有一个神经节点,代表输入层设定条件下的细菌量。
1) 训练集的选取 反向传播神经网络在使用前对它进行训练,根据训练数据调整神经网络中的权值矩阵,直到迭代一定的次数后停止学习。对于1个参数,至少要10个以上训练样本,训练集太小,无法被网络学习[20]。 本实验3个参数有117个样本满足要求。 在输入前将样本随机打乱,并按照8∶8∶1的比例随机分配到训练、测试和验证集中。
2) 数据归一化 不同评价指标的量纲常处于不同的数量级, 为消除特征数据之间的量纲影响,引入归一化。 原始数据经归一化处理后,各指标处于同一数量级,范围在0~1 内。 计算如公式(1):

式中:t' 为归一化数值;t 为实际测定值;tmin为实际测定中最小的一组数值;tmax为实际测定中最大的一组数值。
3) 隐藏层个数和神经元节点数的确定 隐藏层结点数取决于输入、输出的非线性程度,节点数如过多会导致过拟合现象,降低模型的准确性。 根据样本容量选择隐藏层数测试范围为1~3,其中,隐藏层个数为1 时,第一层神经元个数为10~30,步长为2,共15个网络模型;隐藏层为2 时,第一层神经元个数为20~40,第二层神经元为10~35,步长为5,共30个网络模型;隐藏层为3 时,第一层、第二层神经元个数分别为20~35,第三层神经元为10~25,步长为5,共64个网络模型。 比较验证集上均方误差(MSE) 的大小来确定隐藏层个数和神经元节点数,每个网络结构进行3次平行测试,结果取平均值。
4) 模型参数的确定 利用Python 软件建立反向传播神经网络。 为防止反向更新时梯度消失,采用Relu 为网络结构隐藏层的激活函数,归一化的结果在0~1 之间, 输出层的激活函数采用Sigmoid,Dropout 概率为0.5,学习率为0.001,每一轮迭代次数为1500, 每5个样本更新一次梯度。 其中公式(2)为Relu 函数,公式(3)为Sigmoid 激活函数:
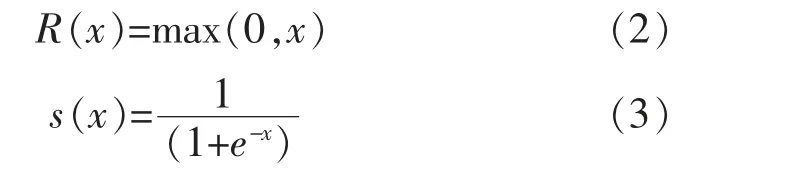
式中:x 为神经元单元的输出值。
1.3.4 修正的Gompertz 模型的建立利用Matlab软件分析不同温度和初始接菌量下金黄色葡萄球菌在酱牛肉中的生长数据,建立生长模型。 修正的Gompertz 模型被广泛应用于拟合微生物量与时间之间的关系。 修正的Gompertz 模型[21]如公式(4):

式中:lg(Nt)为t 时刻细菌的对数值;lg(N0)为初始细菌的对数值;lg(Nmax)为稳定期时最大细菌数的对数值;tlog为延滞期;μmax为最大比生长速率。
1.3.5 模型的评估与验证采用MSE、平方根误差(RMSE)、偏差因子(Bf)和准确因子(Af)来评价模型的可靠性。 其中:

式中:pre 为用模型拟合出的生长数据,即预测值;obs 为实际实验中所测的数据值,即实际值;n 为样本数量。
MSE 评价数据变化程度,值越小,说明模型拟合实验数据的能力强;RMSE 衡量预测准确度,说明模型预测值的离散程度;Af衡量预测值和实际值之间的接近程度,Af>1, 越接近于1 表示模型越准确;Bf表示预测值和实际值之间的偏差,Bf>1,说明预测值偏高,Bf<1,说明预测值偏低。
2 结果与讨论
2.1 反向传播神经网络的建立
人工神经网络数据分为训练集、验证集和测试集,为获得最优的神经网络结构,需确定隐含层的层数和神经元节点数。 依次将训练数据代入隐含层为1~3、节点数为10 到35 的不同的隐藏层网络中,选择验证集上MSE 最小时的节点数作为最优结构。隐 藏 层 数1、2、3 分 别 对 应 的MSE 值 为0.0120、0.0026、0.0029,由此可知当隐藏层数为2 时,MSE值最小, 预测效果优于隐藏层数为1 和3 的模型,故确定该模型的隐藏层数为2。从表1 可看出,当第一层、 第二层神经元节点分别为35、30 时,MSE 值最小,模型预测效果最好。 因此最终的反向传播网络模型结构为2-35-30,网络模型结构见图1。

表1 不同神经元个数的MSE 值Table1 MSE value of different neurons
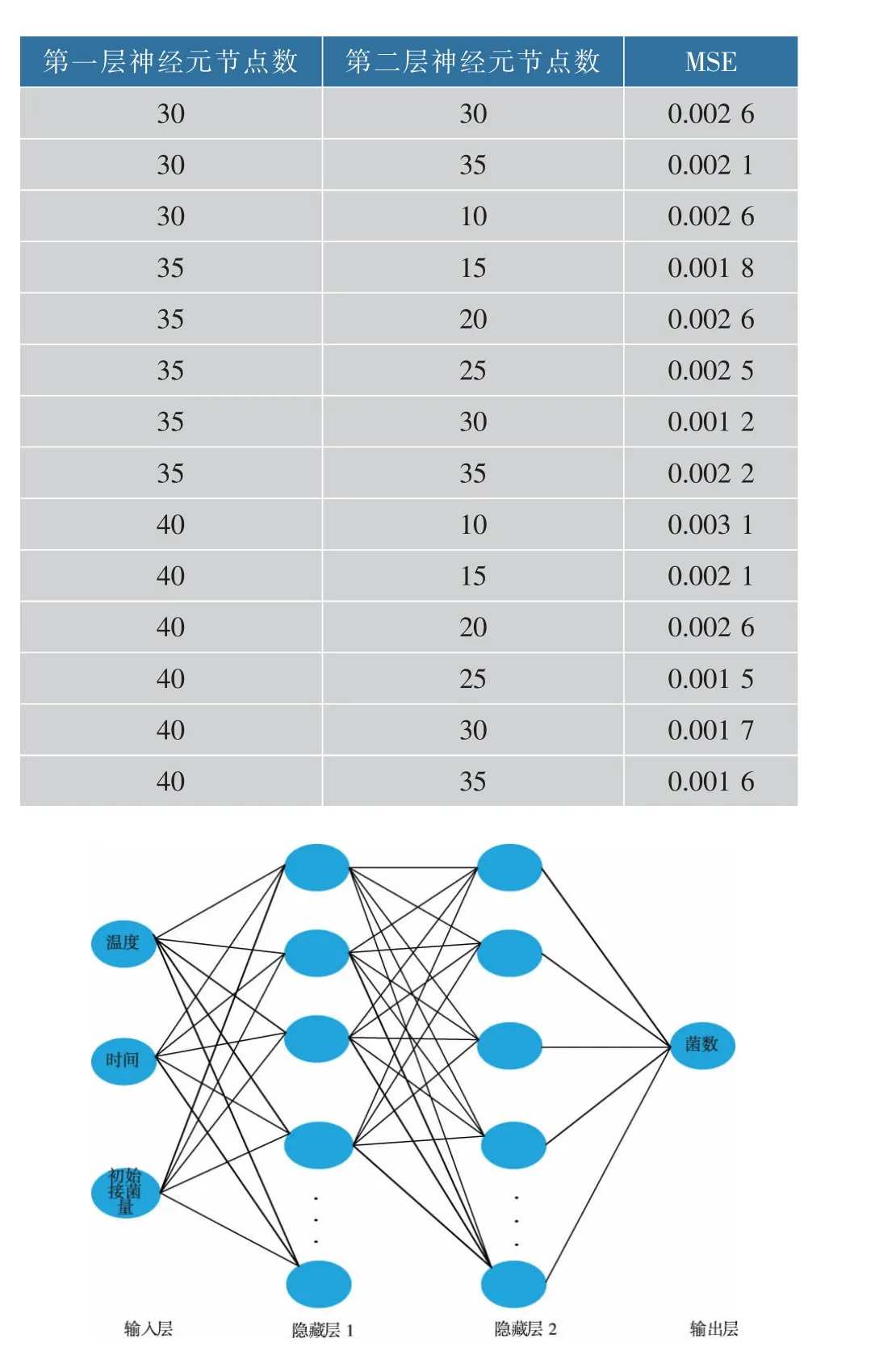
图1 预测酱牛肉中金黄色葡萄球菌生长的人工神经网络结构图Fig. 1 Artificial neural network structure for predicting the growth of Staphylococcus aureus in sauce beef
2.2 酱牛肉中金黄色葡萄球菌生长的修正Gompertz和人工神经网络模型拟合曲线
图2 为不同温度(15、25、36℃)和初始菌数(102、103、104CFU/mL) 组合条件下金黄色葡萄球菌在酱牛肉中生长的一级模型和人工神经网络模型拟合曲线。 可以看出,随着培养时间的延长,金黄色葡萄球菌的浓度也随之增加,且遵循S 形曲线,培养一定时间后金黄色葡萄球菌的生长都趋于稳定。 以修正的Gompertz 模型为基础,得到组合条件下酱牛肉中金黄色葡萄球菌的生长动力学参数最大比生长速率μmax和延滞期tlag,如表2 所示。而神经网络没有确定的函数表达式,无法得到μmax和tlag的值,只能从图中直观表现出细菌的生长状态。 从表2 可以看出,同一初始接菌量条件下,随着温度升高,μmax逐渐增大,15 ℃(0.0524、0.0231、0.0137 h-1)<25 ℃(0.3591、0.2449、0.1488 h-1)<36 ℃(0.4895、0.4459、0.2958 h-1),而延滞期tlag的大小随着温度上升呈现下降趋势,15 ℃(49.67、47.74、46.62 h)>25 ℃(8.5894、7.5110、7.2930 h)>36 ℃(6.4820、6.2551、5.2020 h)这说明温度越高金黄色葡萄球菌的生长速度越快,延滞期越短;同一温度条件下,最大生长速率和延滞期均随着初始接菌量浓度的增加而降低,但变动的幅度小于不同温度组合条件下的最大生长速率和延滞期的数值,这说明不同温度和初始接菌量浓度均影响了酱牛肉中的金黄色葡萄球菌的生长,但温度的影响更大。
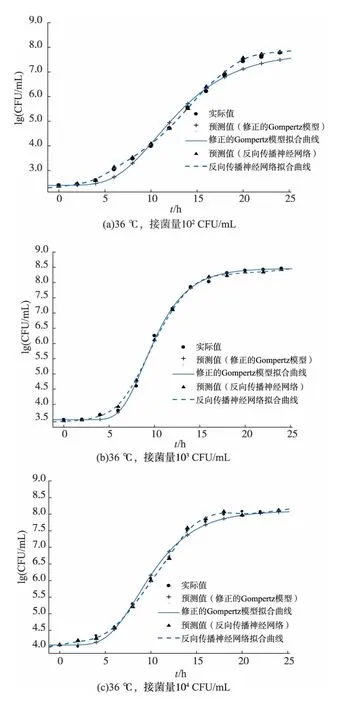


图2 不同温度和初始接菌量条件下金黄色葡萄球的生长Fig. 2 Growth of Staphylococcus aureus under different temperatures and initial inoculation conditions
2.3 模型评估
2.3.1 模型评估在利用训练数据建模的过程中,传统模型和人工神经网络模型都获得较好的拟合度,RMSE、Af及Bf均在理想范围。 与人工神经网络模型相比,传统模型偏差较大,由表3 可以看出,反向传播神经网络模型的RMSE 值均比传统模型的RMSE 值小,这些在Af及Bf上也表现出来,反向传播神经网络模型与修正的Gompertz 模型的Af均大于1 且反向传播神经网络模型的Af相比更接近1,说明前者预测的更接近实际值; 从得到的Bf值看出,反向传播神经网络模型与修正的Gompertz 模型的预测值均在真实值附近上下波动, 由修正的Gompertz 模型得到的预测值比实际值偏小,由反向传播神经网络模型得到的预测值偏差更小,说明该模型的预测效果较修正的Gmopertz 模型更好。
2.3.2 模型验证结合在22、29 ℃条件下获得的实验数据,对建立的反向传播神经网络模型进一步验证其准确性,结果如表4 所示。 从表中可以看出,验证值与预测值的误差均在可接受范围,说明建立的反向传播神经网络模型可预测金黄色葡萄球菌在酱牛肉中的生长。
3 结 语
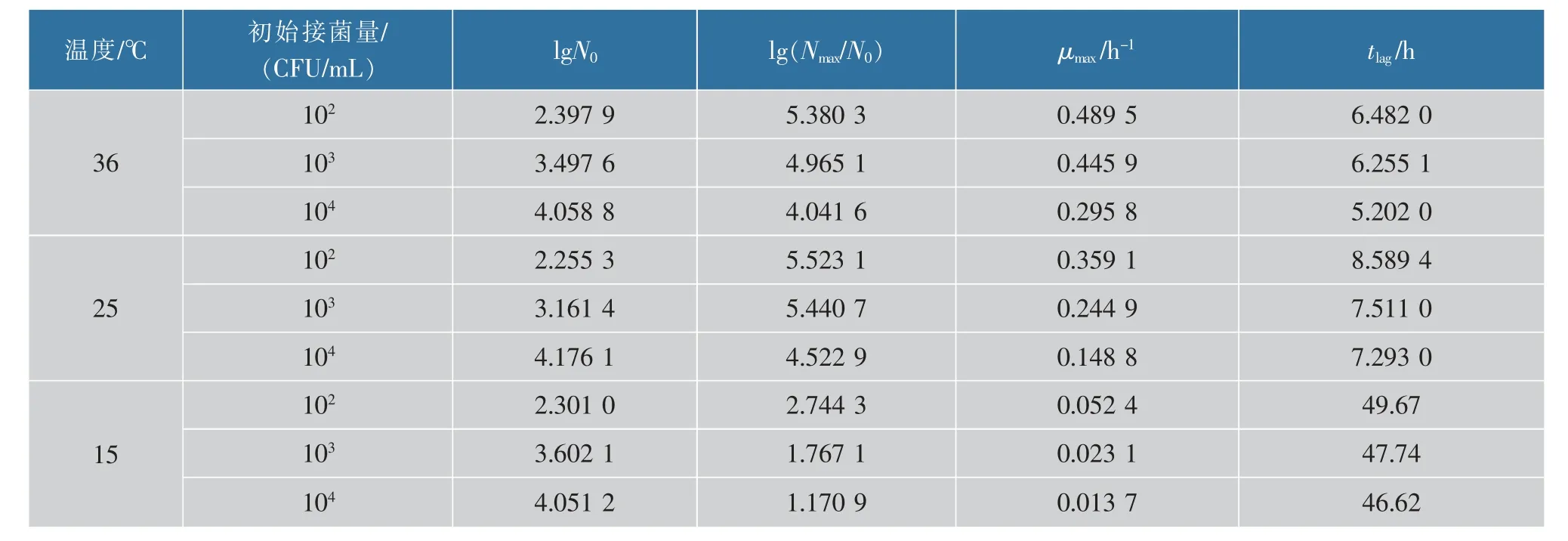
表2 修正的Gompertz 模型拟合得到的金黄色葡萄球菌生长参数Table 2 Growth parameters of Staphylococcus aureus obtained by modified Gompertz model
作者建立的预测模型适合预测多种环境条件下金黄色葡萄球菌在酱牛肉中的生长情况。 在预测准确性方面, 反向传播神经网络优于修正的Gompertz 模型。这是因为修正的Gompertz 模型是经验模型, 通常需要进行校准避免误差的不确定性,当影响金黄色葡萄球菌的生长因素增多时,传统模型会变得复杂,准确率也会降低,因此很难准确地反映环境因素对生长预测的影响。 虽然反向传播神经网络模型无法给出最大比生长速率和延滞期,但该模型在存在不确定数据和测量误差的情况下,会比经验模型产生更准确地预测。 在通用性方面,修正的Gompertz 模型局限性很大,多个影响因素需要多次建模,而反向传播神经网络只需要在模型的输入值中添加所研究的影响因素即可实现预测,大大提高了模型的适用性。 由于酱牛肉的生产、运输、销售过程中温度并非一成不变,在以后的研究中可以考虑在波动温度条件下运用人工神经网络模型来实现更加精确的预测。
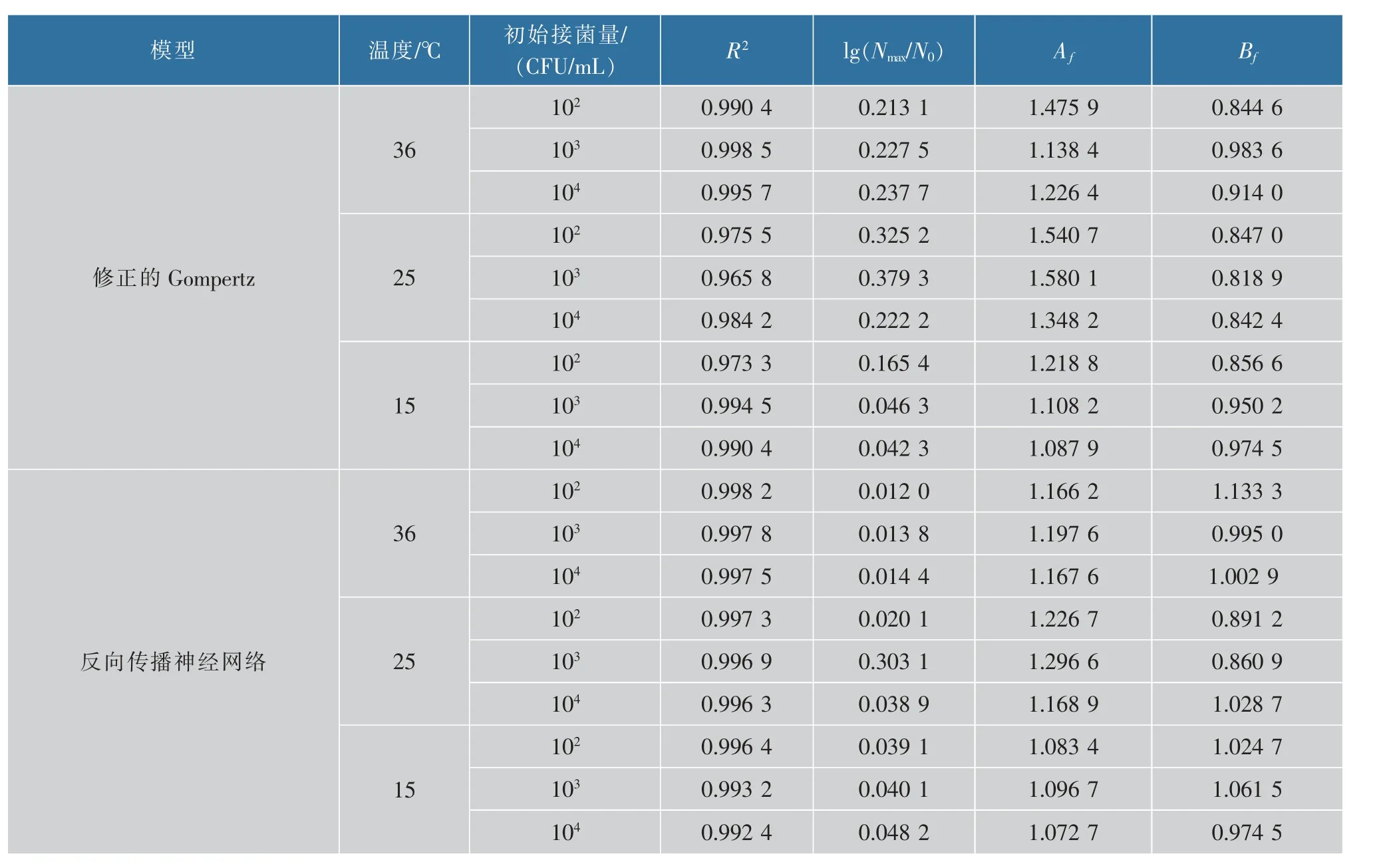
表3 修正的Gompertz 模型与反向传播神经网络比较与评价Table 3 Comparisonand assessment of modified Gompertz model with back propagation neural network

表4 反向传播神经网络模型验证的拟合度指标Table 4 Goodness of fit of verified back propagation neural network models
