知识产权资产证券化的价格敏感度

曲 江，刘洪伟，朱 慧，左妹华

（1.广东工业大学管理学院，广东广州 510520；2.广州大学管理学院，广东广州 510006；3.惠州学院建筑与土木工程学院，广东惠州 516007）

1 研究背景

2019年8月5日，科技部印发《关于新时期支持科技型中小企业加快创新发展的若干政策措施》，指出应从资金、融资与税收层面对科技型中小企业提供产业扶持。新政策鼓励知识产权以质押、投贷联动及融资租赁等方式进行融资，并鼓励为优秀科技型企业进入新三板、科创板上市融资提供便捷通道。但站在企业实际融资角度，科技型中小企业由于存在规模小、实物资产少、自身不确定因素多等条件限制，当前仍较难达到投贷联动、融资租赁与银行抵押融资等条件。科技型中小企业虽然科技成果多、知识产权丰富，但银行在开展质押贷款融资业务时，由于市场状况复杂、知识产权价值评估难度大，银行须进行严格的审批，因此当前质押贷款融资在贷款成本、利息、周期等还不能全面满足我国中小企业的融资需求。随着知识经济的深入发展，为知识付费与知识管理的呼声日趋高涨，无形知识资产在企业与国民经济价值中的占比越来越高，无形知识资产已与实物资产一并成为核心竞争力。拥有自主创新规模与知识含量颇高的国内企业特别是科技型中小企业，如何做好知识与科技项目延伸管理，利用金融工具将知识产权变现，实现企业融资与业务发展，已成为产业科技管理关注的重点。在此背景下，知识产权资产证券化作为一项新兴业务，为我国科技型中小企业融资提供了全新的解决方案［1-3］。

知识产权资产证券化是指企业将自有知识产权授权他人所取回报或衍生债权资产应收账款作资产担保，经组合包装、信用评级增强等，发行为市场上可流通证券，并借以为科创企业融资的金融过程。2019年9月11日，我国首支纯知识产权证券化产品“兴业圆融——广州开发区专利许可资产支持计划”成功发行设立，并在深圳证券交易所正式挂牌转让，标志着政策广泛支持的国内知识产权资产证券化业务正式起步。至2018年年底，我国发明专利拥有量已超160万件，作为新兴业务，企业开展知识产权资产证券化发展空间蔚为可观，如何利用好知识产权资产证券化，做好无形资产评估并准确确定知识产权资产证券化的价格，已成为产业界及学术界急需解决的难题。

知识产权资产证券化涉及价值评估、权益回报、向信托机构转让及证券通过市场发行出售等流程，证券价格的确定是发售成功与否的关键因素。由于无形资产价值评估与知识产权证券价格难于精准估量，且无形资产证券价格同时又受多因素的影响，当各影响要素发生变化时，资产转让与证券价格实际上都会发生敏感性波动，从而影响知识产权资产证券化成功运作。因此，近年来国内中小企业，特别是科技型中小企业开展实施知识产权证券化难度还比较大，门槛也比较高。

为能从理论创新及指导实践两方面为企业开展知识产权资产证券化提供建议，本文以知识产权证券化及证券价格为研究对象，分析影响证券价格的要素并建立证券价格函数模型，研究证券价格函数对各要素变化的敏感程度。首先，通过文献回顾确定知识产权权益价值，分析资产证券化过程中影响证券价格的要素；随后，以金融收益理论为基础，通过知识产权权益未来受让所得收益现金流折现，建立证券价格函数表达式，并研究在各影响因素作用下知识产权资产证券价格函数的敏感度及非线性曲线的变化规律，建立证券价格敏感度度量方法；最后，通过证券价格曲线特征，提出在各影响因素作用下证券价格敏感度度量的误差及改进建议。

2 文献回顾

与产业界利用知识产权开展证券化融资的积极探索类似，近年来学者们从知识产权权益价值评估、权益价值影响因素等方面展开研究，如王炎坤等［4］首先明确科技成果与知识产权的关系，指出科技成果是科技创造者贡献与能力的表现，知识产权是权益的具体体现，知识产权通过专有权方式反映与保护所有人利益。权益价值评估作为权益体现及转让基础，近年来已成为知识产权研究的重点，如吴红［5］将知识产权管理纳入国家企业战略管理，认为制定并做好企业知识产权战略管理是提高企业竞争力的关键；刘伍堂等［6］构建了科技成果知识产权价值评估指标体系，研究科技成果知识产权价值评估及其影响价值的因素，提出了在评估过程中收益额预测、贡献率、收益期限、折现率等参数的确定方法；任丽明等［7］针对多对多知识产权交易市场，将时间、技术、市场、国家政策等因素考虑在知识产权的估价范围，并通过双向拍卖模型推导建立了知识产权转让定价模型；王磊［8］提出了3类知识产权价值评估法（重置成本法、市场价值法、收益法）在市场经济中的作用。在知识产权资产证券化研究方面，谭文俊等［9］将资产权创建作为研究对象并建立影响要素评价模型，认为资产性质、资产归属、资产风险、市场因素、被许可人与管理人以及证券化后影响是资产权构建中的主要影响因素；邵永同等［10］将不同行业组合知识产权作为标的资产，研究组合资产的选择与设置方法，提出了权重设置方法。在证券价格确立及影响要素研究方面，现有文献主要围绕行为要素及变量要素展开研究［11-22］：一是对于信用风险、提前偿付及违约等行为影响要素，主要基于借款人对未来趋势的判断，通过违约风险溢价和真实违约概率进行衡量，建立基于信用风险的提前偿付动机模型，确立证券价格与要素之间的关系；二是在利率、期限、资产价值等影响证券价格的变量要素研究方面，主要以市场完备性为条件，依托无套利定价方法，研究期权定价及变量要素对证券价格的影响。具体证券价格定价与影响要素研究情况如表1示。

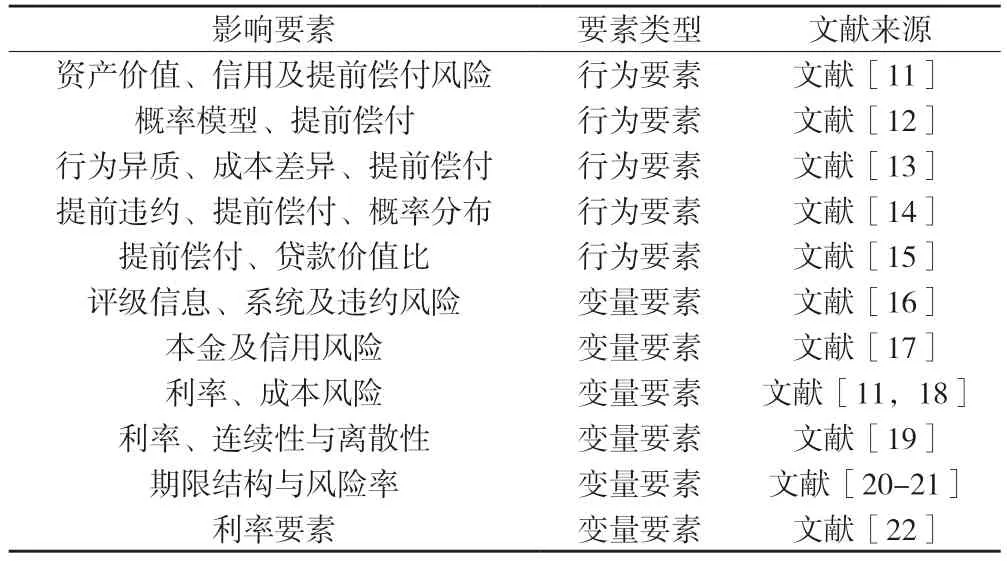
表1 资产证券价格定价与影响要素的主要研究

上述文献深入研究了知识产权权益、价值评估及影响要素，并对资产证券化流程、动力及业务优势展开讨论；通过对利率路径、期限结构的模拟，建立起资产支持证券多种定价模型。研究发现，证券价格除与权益、资产属性及行为因素有关外，还与提前偿付和违约风险、交易成本、证券持有时间、证券到期期数、资产价值、现金流、证券收益率等变量要素及其相互关系有着密切的联系。现有的资产支持证券定价及价格波动研究，主要采取相对估值下的期权定价研究方法，影响价格因素的提前偿付和违约模型实质上是基于市场完备前提下无套利定价方法的一种期权价值计算，但现有研究方法在金融市场不完备时，无套利定价方法与期权价值定价的偏差将会放大，如果与定价相关的利率路径与数据不完整或者口径不相同时，现有基于期权的资产支持证券价格研究将很难做好相关要素变化的证券价格精准度量。

当前我国知识产权资源丰富，知识产权证券化理论创新与寻求实践指导的需求迫切，而现有文献鲜有以知识产权资产证券价格为研究对象，更鲜有建立知识产权资产证券价格模型并开展多维要素变化时的证券价格敏感性研究，因此，本文拟在现有研究的基础之上，围绕知识产权证券价格的影响要素，建立知识产权资产支持证券的价格模型，研究时间、利率等变量变化时证券价格的非线性敏感度，提出知识产权证券价格对各参数变化时敏感性的度量方法。

3 知识产权资产证券价格模型

对确定的现金流和收益率，可通过期限内一系列现金流R(t)的折现值来计算证券价格。由于资产支持证券现金流与通过知识产权权利未来受让所得收益的现金流折现相对应，假设知识产权资产出售与证券发行过程中无其他成本，则此时的知识产权资产价格与证券发行价格相一致。设证券年收益率为i(t)，则资产价值对应的证券价格模型可表示为：

式（1）中，R(t)与i(t)随时间t波动，连续且可导。对于个现金流，一年复利m次的年名义利率，则名义收益率用利息力（即累计函数相对变化率）δ表达证券投资人在时点上的获利能力：

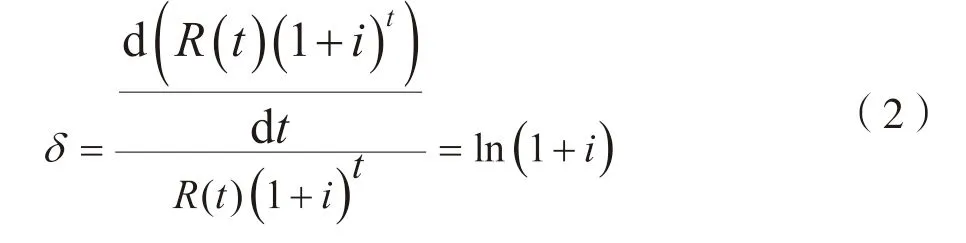
由于δ连续可导，假设i(t)与i(m)(t)均不随时间发生平移，当时，证券价格函数可用利息力δ表达：

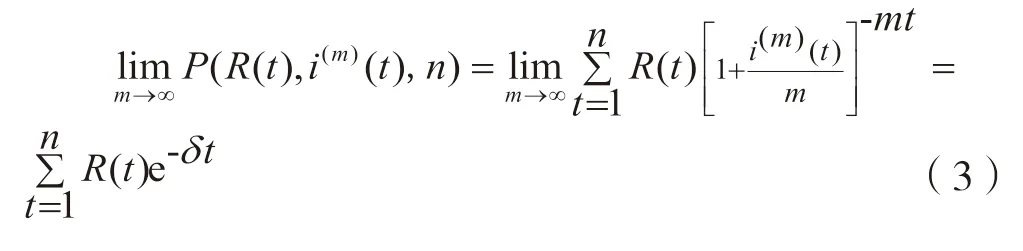
结论1：知识产权资产支持证券价格函数可用证券期限内知识产权权利未来受让所得收益现金流折现来表达，价格函数影响要素包括证券年收益率、定期收益现金流及证券的发行期限。

4 知识产权资产证券价格敏感度

相比实物资产证券化，无形知识产权资产更容易受到技术更新迭代、市场竞争、消费观念转变及外部侵权等因素变动的影响，因此通过知识产权权利未来受让所得的预期经济收益现金流折现及相应的资产证券价格也会受到影响，从而研究知识产权资产证券价格在各个要素变动时的敏感度波动，具有十分重要的现实意义。

4.1 知识产权资产证券价格对时间的敏感度

随着证券周期拉长，知识产权资产受市场、政策、流动性、利率的影响越多，对应的证券价格（P）波动越大，证券风险越高，甚至知识产权的所有者更有丧失未来许可使用费收入的风险，并且即使资产到期时间一致，但到期期数不同，证券价格对应的利率等风险也不相同。那么，如何界定证券价格对时间风险的度量，本文将久期利率风险理论引入知识产权资产证券价格敏感度分析。考虑到货币时间价值，本文将知识产权权利未来不同时段内所得经济收益对应的时间价值作为度量敏感度的标准，用未来现金流到期时间的加权平均值，即马考勒久期（D）来度量资产价格对时间的敏感性：

结论2：在现金流与收益率保持不变的情况下，知识产权资产支持证券价格风险与时间与到期期限有关，证券到期期限越长，现金流变化越频繁，证券价格变化越大，风险越高。

4.2 知识产权资产证券价格对收益率的敏感度

假定R(t)与i(m)(t)不随时间平移，用洛必达法则可证明，当以利息力δ为变量，MacD为因变量，对马考勒久期理论展开研究，设利息力δ连续，MacD可导，则对MacD取偏导数，有：

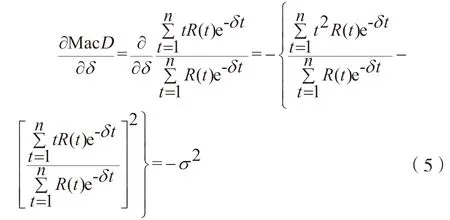
由于MacD对利息力变量δ的一阶导数为负，MacD是利息力δ的减函数，也就是收益率的减函数，因此收益率越高，MacD越小，即证券价格的时间风险越低，知识产权资产支持证券价格对收益率变动的敏感性越低。用示证券价格的瞬时变化速率，则：

用K表示消除资产规模及为负的影响，表示证券价格随收益率变化的速率，可看作证券价格曲线的斜率。由于已证明MacD是利息力δ的减函数，也是收益率的减函数。因此，当收益率越高、斜率越大时，知识产权支持证券利率风险越小，证券价格受收益率变化影响的敏感性越低。继续变量替换微分值，可得：

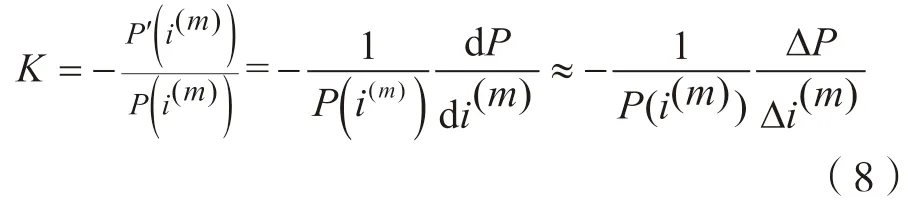
变换式（8），并按百分比表达变化率，可得：

即当收益率i(m)变化时，可使用斜率估算出证券价格的变化率与敏感度。

结论3：在现金流与收益率不随时间平移的条件下，知识产权资产支持证券的价格对收益率变化的敏感度可用价格非线性曲线的斜率进行估算，并且证券收益率越高，证券价格曲线的斜率越大，证券价格对收益率变动的敏感性越小，利率风险越低。

如果现金流与收益率随时间发生平移，或现金流本身对收益率变化敏感，那么上述马考勒久期的时间敏感性与利率敏感性函数将不再适用，因此不能直接计算如图1所示，假设当收益率增加时，证券价格为P+；当收益率减少时，证券价格为P-。则可以用模拟对照证券价格曲线变化，此时实际以割线AB的斜率替代了点(y0，P0)的切线斜率，即用估计值替代假设则。因此，即如果现金流与收益率随时间发生平移，则可以用近似模拟证券价格对收益率的敏感度。

图1 证券价格模型函数曲线

4.3 非线性误差与度量的改进

图2 弧度差异的证券价格模型函数曲线

由于C是i(m)的减函数，因此在R(t)、i(m)(t)不随时间平移的情况下，i(m)(t)变化越大，弧度C值越小，价格曲线的弯曲程度越小，而i(m)(t)变化越小，C值越大，价格曲线的弯曲程度越大。

考虑在单点i(m)(t)=i0时，对知识产权资产支持证券价格表达式用泰勒级数展开：

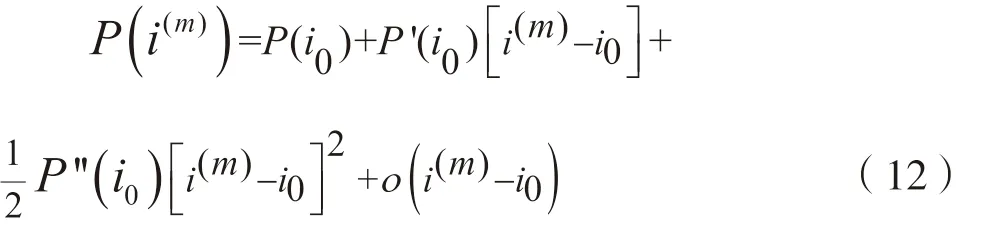
将P(i0)移到等式左边，两边再同时除以P(i0)，并忽略作为的高阶无穷小量的影响，可得：

即证券价格对利率变化的敏感度可用曲线斜率与弧度进行修正表达，其中i(m)(t)上升时斜率K增加，证券价格降幅增加，此时对证券投资人不利；i(m)(t)下降时K增加，但证券价格上浮增加，对证券投资人有利。但无论i(m)(t)如何变化，证券C值均正向增加，因此证券价格上升，均对证券投资人有利。

结论4：当证券收益率变化时，知识产权资产支持证券价格函数曲线的斜率K较小而弧度C值越大，风险越低，此时对知识产权资产支持证券投资人越有利。

4.4 组合知识产权资产支持证券价格对收益率的敏感度

科技型中小企业知识产权多，在实际资产证券化融资过程中，企业会将无形资产组合打包，建立资产池并实施资产证券化，对于证券组合则可以评估证券开展对时间与收益率的敏感度。由于连续且可导，因此对于有n种知识产权资产支持证券的组合，可分别计算每种证券的久期，并结合每种知识产权在组合证券中的权重，通过计算加权平均数，从而评估证券组合的时间敏感度。如对于一系列证券该组合证券的价格为组合证券的马考勒久期为：

即证券组合对时间的敏感度可用组合久期进行度量。

由于证券曲线的非线性特性，并且组合证券对收益率的敏感度通过曲线的斜率K与弧度C值进行度量，因此可以将证券组合设定为一种证券，并将证券组合的现金流视为设想证券的现金流，通过设想证券的综合收益率变化情况来综合评估组合证券价格的敏感度。此外，在业务开展过程中，如果权利受让人提前偿付或出现违约行为，此时知识产权权利未来受让与现金流提前终止，证券价格的杠杆作用消失，则证券价格应依照知识产权对应重置成本或市场价值进行估算，此时证券价格将受提前偿付和违约行为的影响而迅速降低。

结论5：组合知识产权资产支持证券价格对收益率的敏感度可通过计算每种证券的敏感度进行测算，对收益率的敏感度测算可将组合证券当作一种证券，并通过曲线的斜率K与弧度C值进行测算。

5 结论

我国科技型中小企业众多，知识产权规模与企业资金需求量大，本文从适合我国中小企业融资国情的知识产权资产证券化业务出发，首先分析了知识产权资产证券价格的影响要素，包括证券持有时间、证券到期期数、证券价格、每期现金流、证券收益率，基于现金流收益贴现与偏微分导数，通过精算与数学推导建立了证券价格函数模型；然后，研究了证券价格对时间、收益率等参数变化的敏感性，对马考勒久期理论进行了延展研究，验证了证券到期期限越长、证券价格变化越大，证券持有风险越高，而证券收益率越高，证券价格对收益率变动的敏感性越小，证券持有风险越低，发现组合证券价格对时间的敏感度可通过计算每种证券的敏感度进行测算，组合证券价格对收益率的敏感度则可将组合证券当作一种证券进行度量；最后，结合敏感度度量的非线性误差分析，引入非线性曲线斜率与曲线弧度概念，将证券价格函数进行泰勒级数展开，优化资产价格对利率变化的敏感度度量方法，证明了证券价格函数曲线的斜率较小而弧度越大，利率风险越低，对知识产权资产投资人越有利。

本文关于知识产权资产支持证券价格对时间与利率变化的敏感度分析，均限定在未出现违约行为、收益率没有平移及每期现金流不发生变化的假设下，实际利率风险的估算误差还没有考虑利率期限结构、随机等因素，在证券持有与交易过程中还存在利率自身随机变化等因素，今后可对此模式进行全场景、深入的研究。