隔板结构参数对EFP成型的影响

贺金金， 梁增友， 邓德志， 杨成龙， 张智超

(中北大学 机电工程学院， 山西 太原 030051)

0 引 言

爆炸成型弹丸(EFP)具有对炸高不敏感、 反应装甲对其影响小、 侵彻后效大等优点[1]， 因而得到了弹药领域专家们的密切关注， 并且已应用于各种反装甲武器系统中. 国内外学者对EFP成型及对目标的毁伤效应进行了大量研究， 研究发现， 通过在聚能装药结构中加入隔板， 可以有效控制装药内爆轰波的传播途径和波形形状， 从而提高其毁伤效能. 张先锋[2]等人研究了无隔板和有隔板的EFP战斗部的成型情况， 数值模拟和试验结果表明， 有隔板的比无隔板的EFP战斗部有更高的初速和更大的长径比. 李如江[3]等人研究了隔板形状对聚能射流的影响， 在射流头部速度方面， 双截锥形较截锥形隔板提高了约9%. 付建平[4]等人通过数值模拟和静破甲试验对带隔板的聚能射流进行了研究， 结果表明， 在带隔板的聚能装药结构中， 合适的罩顶药高能提高破甲威力.

在EFP战斗部中嵌入隔板， 隔板必须具有隔离爆轰波的能力， 所以隔板的厚度不能太小， 又因为在装药结构中两侧的爆轰波压力小于中间的压力， 故隔板两侧的厚度不需要太大， 所以本研究中将EFP战斗部内隔板的外形设计为柱锥形， 然后利用LS-DYNA仿真软件得出隔板的各个结构参数对EFP成型的影响规律.

1 隔板作用原理与影响分析

1.1 隔板作用原理分析

在EFP战斗部结构中嵌入隔板， 调整了爆轰波的传播方向， 使得爆轰波阵面与药型罩壁面的夹角变小， 而夹角一旦变小会导致作用在药型罩上的压力变大， 从而有利于提升EFP的速度、 增加长径比[5]. 有无隔板的EFP战斗部装药结构如图 1 所示， 爆轰波形有以下两种形式：

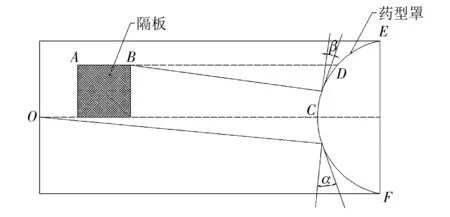
图 1 有无隔板的情况下EFP战斗部结构 及爆轰波形示意图Fig.1 EFP warhead structure and detonation waveform diagram with or without baffles

上半部分为有隔板的情况， 由于爆轰波的传播满足光学传播原理， 中心点起爆后形成的爆轰波会绕过隔板继续传播， 因此后续的爆轰波可看成由新的起爆点所发出的， 如图 1 所示， 拐点A、B成为了新的起爆点， 从点O起爆后， 爆轰波形成并绕过隔板到达拐点A， 拐点A成为新的起爆点发出爆轰波， 然后发出爆轰波绕过隔板到拐点B， 拐点B又将作为新的起爆点发出爆轰波， 另外作用于药型罩CD段上的爆轰波可看作是从拐点B发出的， 作用于DE段上的爆轰波可看作是从拐点A发出的. 下半部分为无隔板的情况,根据光学传播原理， 中心顶点起爆后， 爆轰波会以类似于球面波的形式在EFP战斗部内进行传播， 最后直接作用于药型罩上.

1.2 爆轰波阵面和药型罩壁面夹角的计算

由于爆轰波阵面和药型罩壁面夹角的大小会影响到爆轰波作用在药型罩微元上的压力， 进而影响EFP的速度和长径比. 因此下面对夹角值的大小进行计算和分析.

1) 无隔板时夹角的计算

在无隔板的情况下， 爆轰波阵面和药型罩壁面的夹角计算示意图如图 2 所示.

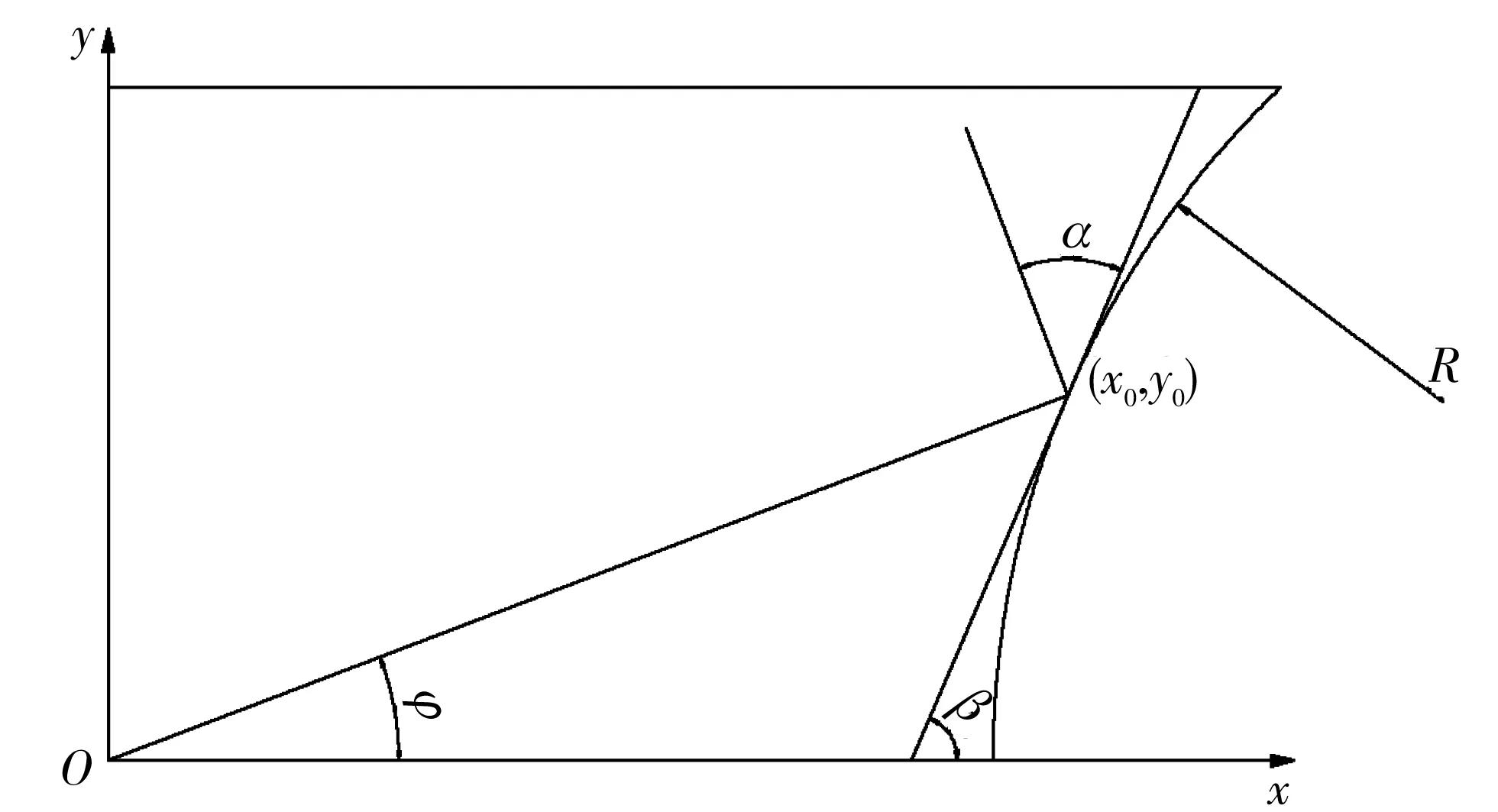
图 2 无隔板时爆轰波与药型罩壁面 的夹角计算示意图Fig.2 Schematic diagram of the calculation of the angle between the detonation wave and the wall surface of the liner without partition

爆轰波会以类似于球面波的形式在EFP战斗部中进行传播[6]， 结合波的传播原理以及几何关系可得， 夹角的计算公式为

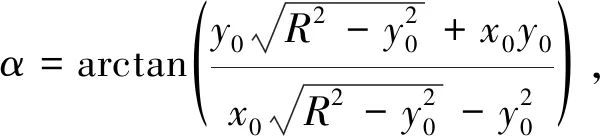
(1)

式中：β为药型罩微元对应的直线的倾斜角；x0为药型罩微元的横坐标；y0为药型罩微元的纵坐标；R为药型罩圆弧的曲率半径.

2) 有隔板时夹角的计算

在有隔板的情况下， 由于爆轰波的传播满足光学传播原理， 根据光学传播原理分析可得， 整个计算分为两个阶段， 分别为起爆点A作用的DE段和起爆点B作用的CE段， 而DE段的计算原理和上面的无隔板情况相同， 这里就不进行计算了， 只计算起爆点B作用的CE段. 爆轰波与药型罩壁面的夹角计算示意图如图 3 所示.

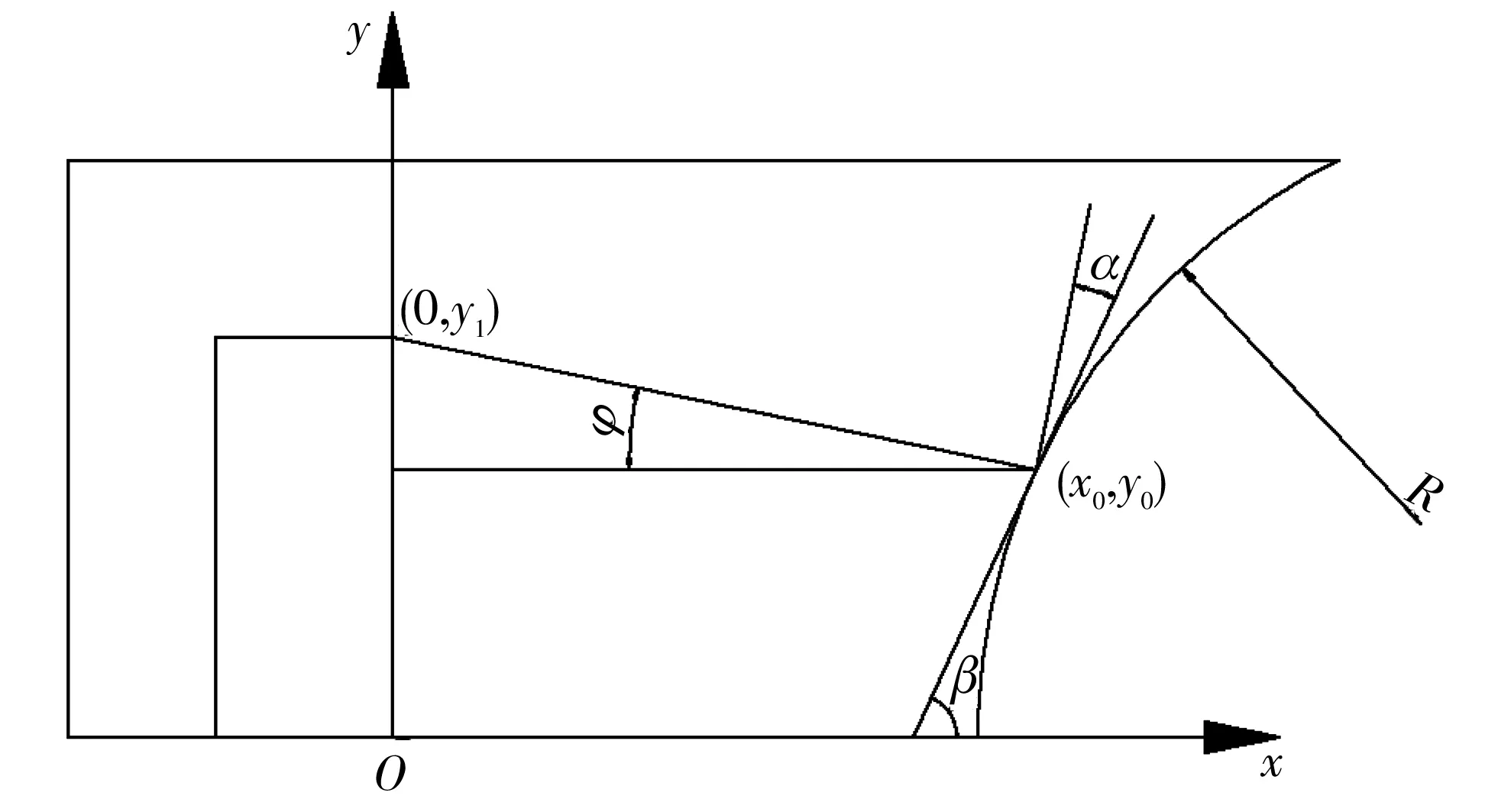
图 3 有隔板时爆轰波与药型罩壁面的夹角计算示意图Fig.3 Schematic diagram of the calculation of the angle between the detonation wave and the wall surface of the liner with partition

结合波的传播原理和图中的几何关系可知，CE段夹角的计算公式为

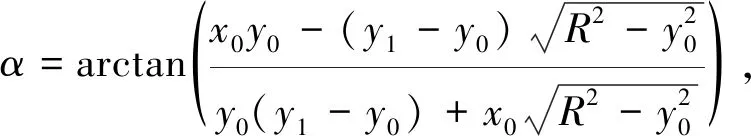
(2)

式中：β为药型罩微元对应的直线的倾斜角；x0为药型罩微元的横坐标；y0为药型罩微元的纵坐标；y1为隔板外侧起爆点的纵坐标；R为药型罩圆弧的曲率半径.

在有无隔板这两种情况下， 药型罩与爆轰波夹角α随圆弧长度L的变化规律计算结果如图 4 所示， 由图 4 可知， 在药型罩的大部分区域内， 有隔板的爆轰波与药型罩壁面的夹角小于无隔板的， 所以， 在聚能装药结构中适当地嵌入隔板在一定程度上减小了爆轰波与药型罩壁面的夹角， 有利于提升EFP的速度、 增大EFP的长径比.

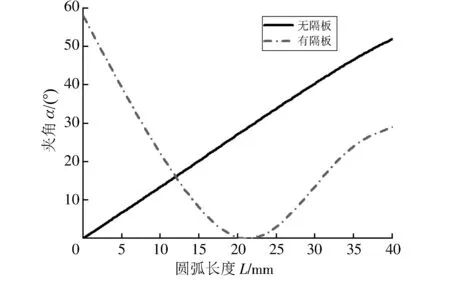
图 4 有无隔板情况下夹角与圆弧长度的变化规律Fig.4 Variation of the angle and the length of the arc with or without a baffle

2 结构设计与仿真

2.1 带隔板EFP战斗部结构设计

基于对球缺形药型罩及带隔板的EFP战斗部结构的大量研究[7]， 设计了如图 5 所示的球缺形带隔板的EFP战斗部， 起爆方式采用中心定点起爆. 其中， 装药直径D为80 mm， 装药高度为80 mm, 曲率半径为80 mm， 隔板直径为0.4D， 隔板总厚度为35 mm， 隔板圆柱部高度为15 mm， 罩顶药高为24 mm. 影响规律研究所涉及的因素有隔板直径d、 隔板圆柱部宽度s、 罩顶药高h.

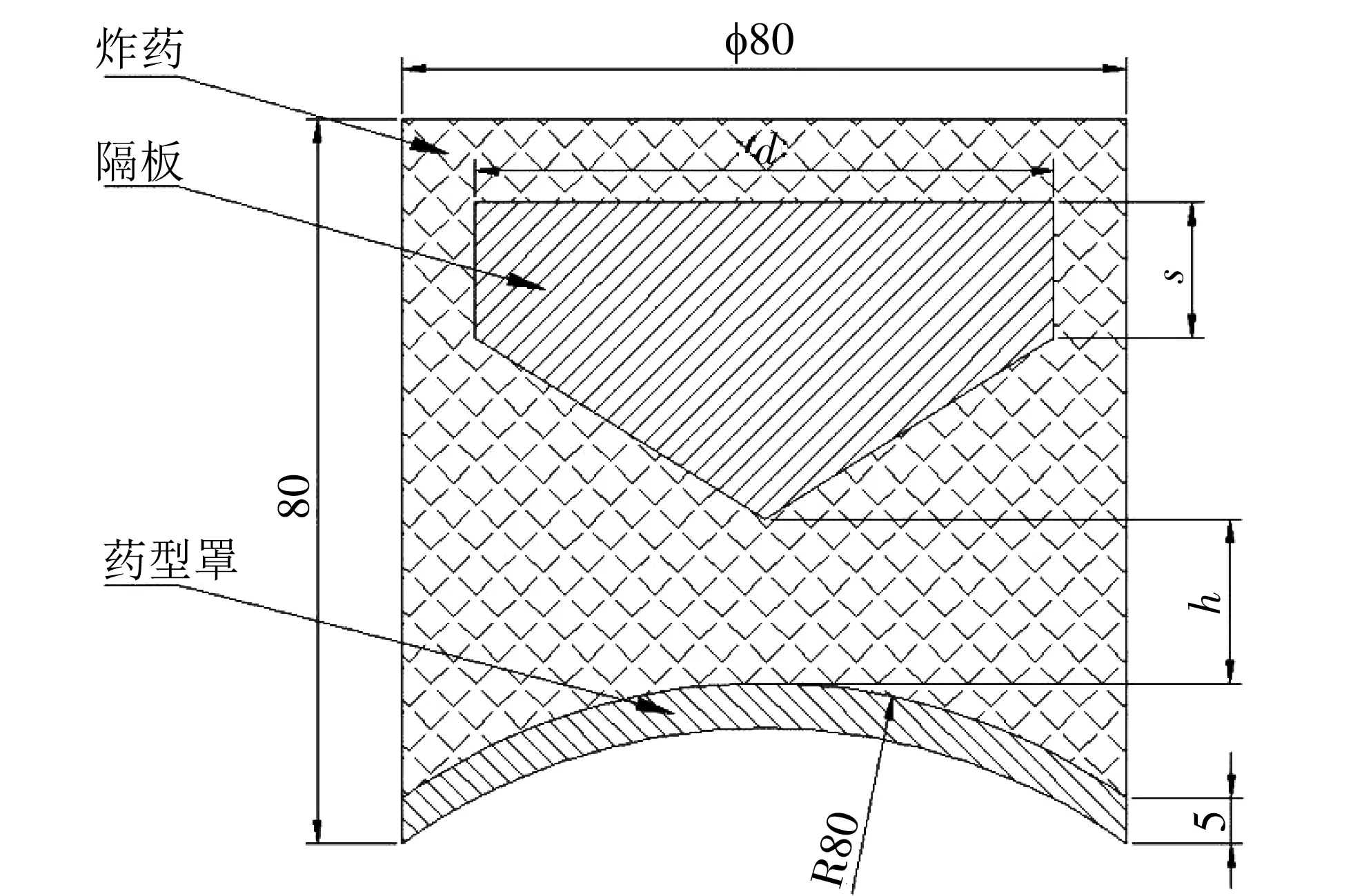
图 5 球缺形带隔板的EFP战斗部结构图Fig.5 EFP warhead structure with a ball-shaped missing partition

2.2 仿真模型及研究方案

本研究建立的有限元模型如图 6 所示， 所有计算网格采用六面体实体单元， 聚能战斗部的隔板、 装药和周围空气域单元采用Euler算法， 药型罩单元采用Lagrange算法， 采用LS-DYNA软件进行仿真计算. 药型罩材料采用紫铜， 本构方程选用Johnson-Cook模型[8], 状态方程选取Gruneisen方程； 主装药采用8701炸药， 状态方程选取JWL方程； 空气采用Null模型和Linear-Polynomial线性多项式状态方程； 隔板材料选用聚氨酯， 采用Elastic-Plastic-Hydro模型Gruneisen状态方程. 为了获得隔板各结构参数对EFP成型的影响规律， 采用控制变量法， 即保持其中两个参数不变， 研究第三个参数对EFP成型的影响[9].

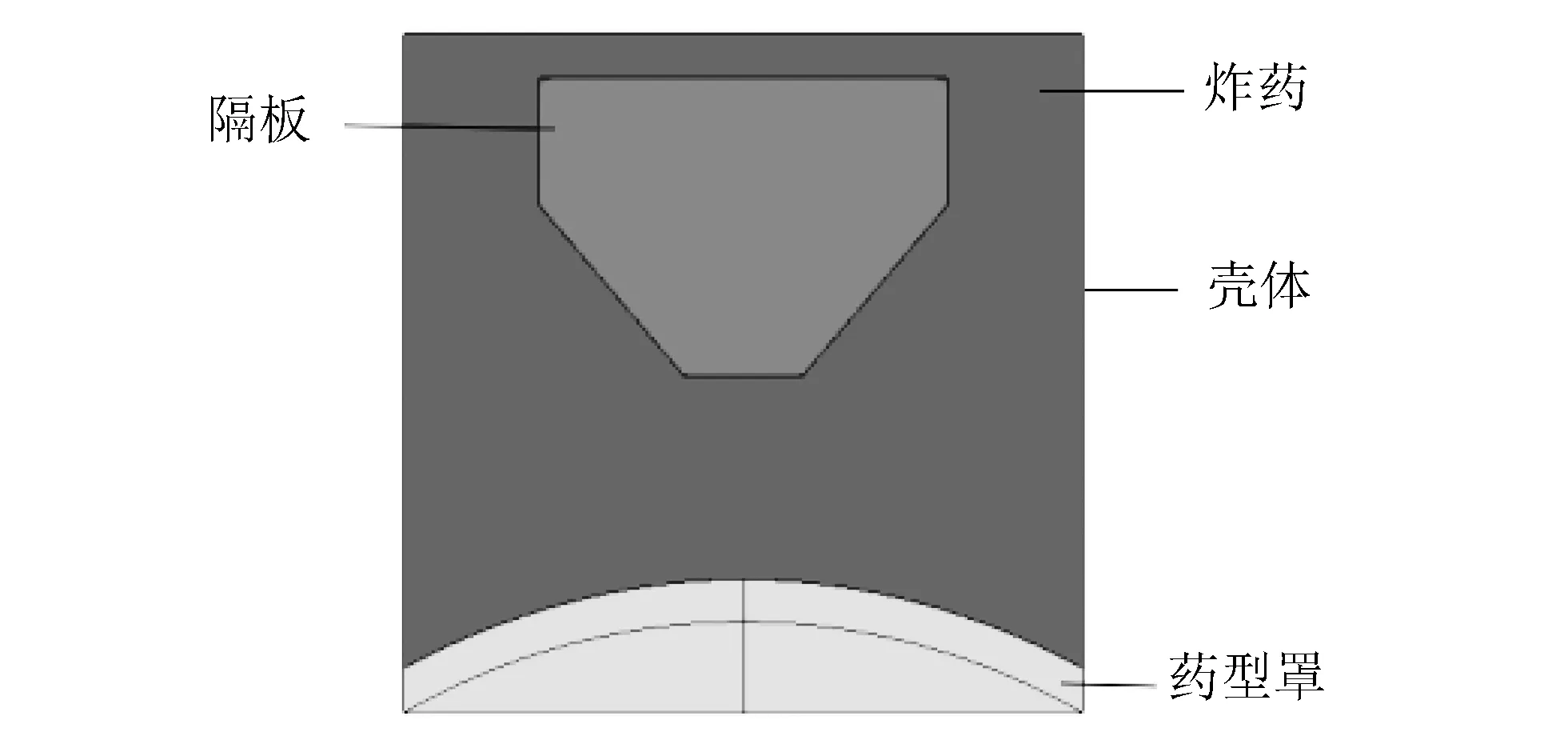
图 6 球缺形带隔板的EFP战斗部仿真模型Fig.6 EFP warhead simulation model with spherical shape missing partition

3 隔板结构参数对EFP成型性能的控制规律

3.1 隔板直径的影响

选取s=15 mm,h=24 mm, 对隔板直径d为0.2D、 0.4D、 0.6D的3个方案进行数值仿真， 如图 7 所示为每个方案在100 μs时刻EFP的成型状态.

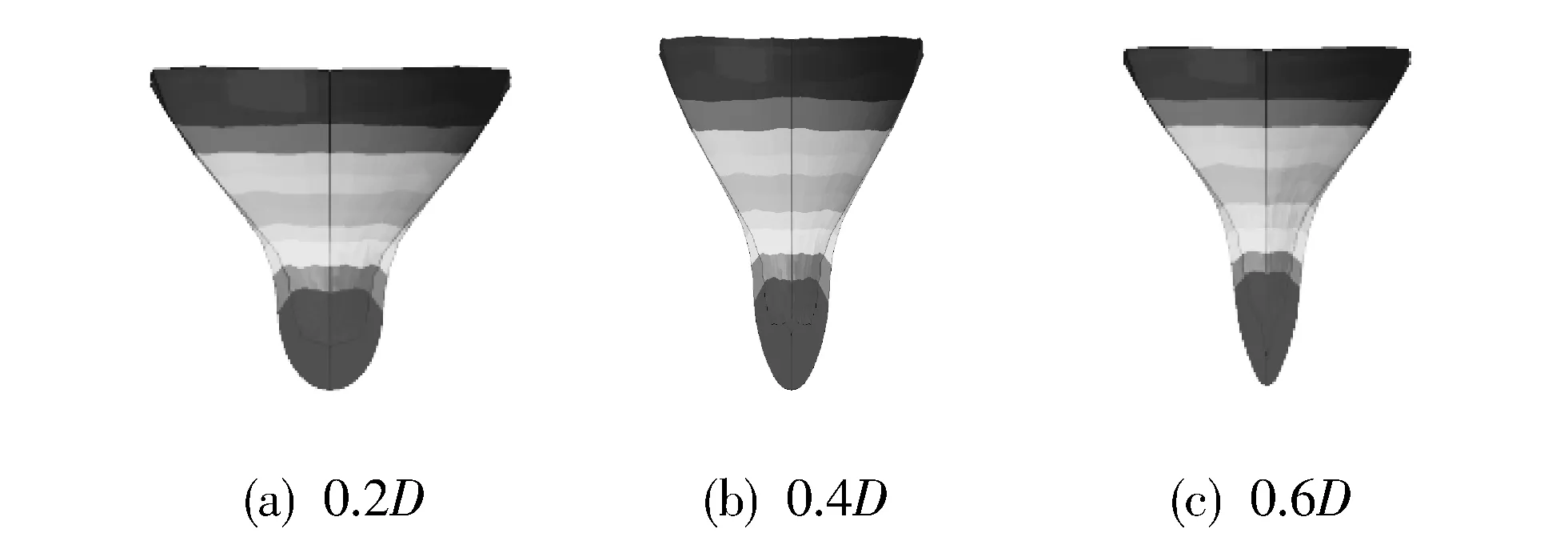
图 7 不同隔板直径100 μs时刻的EFP速度云图Fig.7 EFP velocity cloud map of different separator diameters at 100 μs

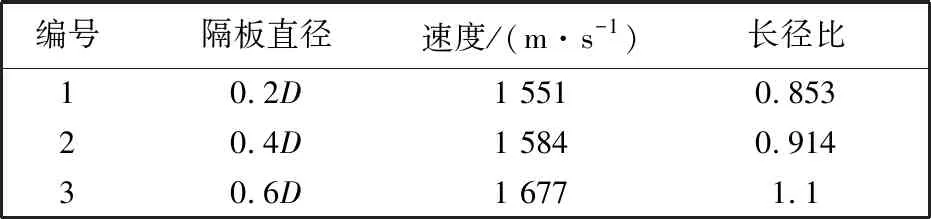
表 1 隔板直径对EFP头部速度和长径比的影响

由图 7 和表 1 可知， 保持隔板外形不变， 随着隔板直径的增加， EFP头部速度呈增加的趋势， 且长径比也在不断增大. 由于隔板直径的逐渐增加， 爆轰波阵面与药型罩壁面的夹角逐渐减小， 导致药型罩微元压力逐渐增加， 药型罩微元速度逐渐增加， 药型罩径向收缩速度增加， 从而EFP速度逐渐增加， EFP的长径比逐渐增加. 综合分析， 隔板直径的变化对EFP速度的影响是比较小的， 而对EFP长径比的影响是较大的， 考虑EFP的成型状态， 选取隔板直径为0.6D较为合适.

3.2 隔板圆柱部高度的影响

选取d=32 mm，h=24 mm， 对隔板圆柱部高度s为15, 25, 35 mm的3个方案进行数值仿真， 如图 8 所示为每个方案在100 μs时刻EFP的成型状态.

由图 8 和表 2 可知， 当保持隔板外形不变时， 随着隔板圆柱部高度的增加， EFP速度呈逐渐减小的趋势， 同时长径比也在不断减小. 由于隔板圆柱部高度的逐渐增加， 爆轰波波阵面和药型罩壁面的夹角逐渐增加， 导致罩微元压力逐渐减小， 药型罩微元速度逐渐减小， 药型罩径向收缩速度减小， 从而EFP的速度逐渐减小， EFP的长径比逐渐减小. 综合分析， 隔板圆柱部高度的变化对EFP速度和长径比的影响是比较小的， 选取隔板圆柱部高度15 mm较为合适.

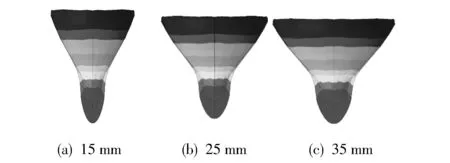
图 8 不同隔板圆柱部高度100 μs时刻的EFP速度云图Fig.8 EFP velocity cloud diagram of the height of the cylindrical part of different partitions at 100 μs

表 2 隔板圆柱部高度对EFP速度和长径比的影响

3.3 罩顶药高的影响

选取为d=32 mm，s=15 mm, 对罩顶药高h分别为20， 24， 28 mm的3个方案进行数值仿真， 如图 9 所示为每个方案在100 μs时刻EFP的成型状态.

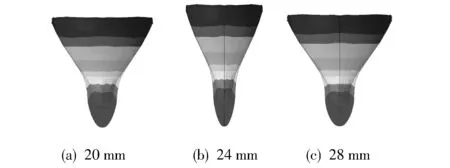
图 9 不同罩顶药高100 μs时刻的EFP速度云图Fig.9 EFP velocity cloud map of different heights of the top of the diaphragm at 100 μs

由图 9 和表 3 可知,保持隔板外形不变， 随着隔板与药型罩距离的逐渐增加， EFP头部速度呈现增加的趋势， 而长径比的变化规律为先减小后增大. 随着罩顶药高的增加， 虽然爆轰波与药型罩壁面的夹角没有发生改变， 但马赫波的形成影响着EFP的速度和长径比. 综合分析， 为避免EFP在成型过程中由于速度过高导致头部破裂， 选取罩顶药高为24 mm较为合适.

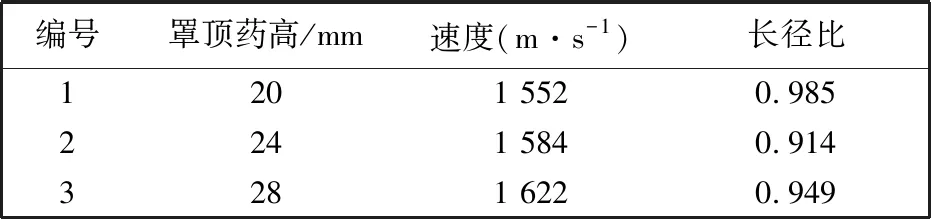
表 3 罩顶药高对EFP速度和长径比的影响

4 隔板结构的优化

4.1 正交设计方案

在EFP战斗部装药结构一定的条件下， 对隔板结构进行正交设计[10]. 通过模拟仿真， 计算得出隔板直径d、 隔板圆柱部高度s、 罩顶药高h这三种因素对EFP成型影响的主次顺序， 获得EFP战斗部装药结构参数下隔板的最佳结构尺寸.

隔板直径d、 隔板圆柱部高度s、 罩顶药高h这3个隔板结构参数作为正交优化设计的3个因素， 每个因素选取3个水平， 参与正交优化计算， 每个因素及对应的3个水平见表 4， 根据L9正交表[11]， 选取3因素3水平进行9次仿真计算. 通过正交表选取的试验次数， 具有均匀分布、 代表性强的优点， 并且使得整个试验的工作量下降， 节省了整个试验的工作时间， 降低了整个试验的成本， 加快了整个试验的进程， 因此正交设计在各行各业中都得到了广泛的研究和应用.

表 4 正交试验的各因素水平表

4.2 计算结果及分析

将EFP速度和长径比作为优化设计实验的评价指标. 各组合计算结果如表 5 所示， 其中d，s，h分别为隔板直径、 隔板圆柱部高度、 罩顶药高的水平数.

利用极差法对这9次仿真的计算结果进行分析： 将表 5 中每列水平数相同的结果数据进行相加， 1， 2， 3每个水平的计算结果分别为K1，K2，K3， 然后将它们分别除以3， 最后将这些结果中的最大值减去最小值得到极差S[12]. 通过对极差S的比较即可得出各个因素对指标(速度和长径比)影响的主次顺序. 表 6 为各个因素影响下对应各个指标的极差. 通过计算比较可得： 对速度影响的主次顺序为h，s，d， 对长径比影响的主次顺序为d，h，s.

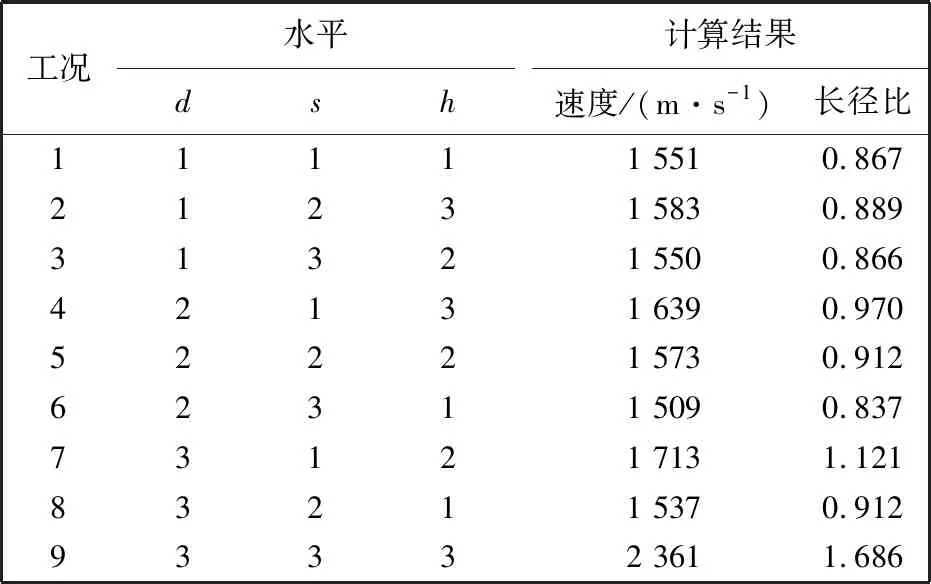
表 5 正交试验方案表

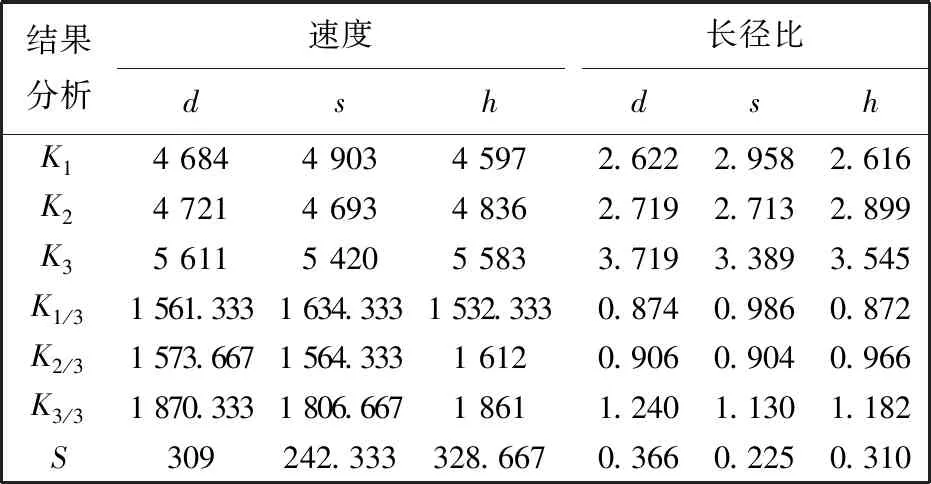
表 6 正交试验计算表

5 结 论

通过仿真模拟研究了隔板各结构参数对EFP成型的影响， 得出了以下结论：

1) 以装药口径80 mm、 药型罩曲率半径和厚度分别为80 mm和5 mm的球缺形EFP战斗部结构为例， 通过数值模拟得出了不同因素对EFP成型过程中速度和长径比的影响， 获得了EFP成型状态较好的隔板结构参数取值组合， 其中隔板直径d为48 mm， 隔板圆柱部高度s和罩顶药高h分别为15 mm和24 mm.

2) 利用正交优化的设计方法， 通过模拟仿真， 计算得出隔板结构各因素对速度影响的由主到次的顺序为h，s，d， 对长径比影响的由主到次的顺序为d，h，s.