基于结构诸元的枪械方案评价
2020-09-10张登谦王惠源刘科研陈锦喜
张登谦, 王惠源, 刘科研, 袁 安, 陈锦喜
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 重庆建设工业集团, 重庆 400050;3. 中国人民解放军63936部队, 北京 102202)
0 引 言
枪械方案评价贯穿于枪械研制的全过程, 能否有效筛选出较优设计方案直接影响枪械研制周期和费用. 在枪械研制不同阶段的方案评价指标具有不同的特点, 在方案研制初期, 评价指标值多为专家主观给出, 使得评价客观性较低, 结果可解释性较低, 随着研制工作逐步推进, 指标值逐渐可以通过试验、 测量等方法客观给出, 则评价客观性会逐渐较高, 结果可解释性也随之提高. 因此, 有必要针对枪械研制不同时期, 采用差异性的枪械方案评价方法.
目前, 国内外的枪械方案评价[1-7]多针对枪械方案研制的中后期, 指标可以通过实验、 测量等手段获得, 并且基于战术技术指标对方案进行评价, 其指标值较为准确、 客观, 评价结果可信度高, 例如楼俐[8]采用全枪质量、 全枪长度等评价指标, 其评价指标数据较为准确, 评价结果客观性较高. 对于武器方案研制初期, 多基于主观定性给出数据进行评价, 评价主观性较强, 例如余俊[9]采用了毁伤概率、 战斗射速和人机功效等评价指标, 评价数据通过主观给出, 其评价结果主观性较强, 且指标综合性较强. 对方案研制初期方案的评价应尽量客观, 并且对方案设计要有较好的指导作用, 而基于战术技术指标的评价指标较为笼统. 因此, 本文首先针对枪械方案研制初期方案评价主观性强的问题, 提出一种基于结构诸元的评价指标体系, 即在基于战术技术指标的基础上, 将其扩展到结构诸元层次, 然后构建各指标对应的基于结构诸元的数学模型及计算方法, 能有效提高评价结果的客观性, 对方案设计也可起到较好的指导作用.
1 评价指标
1.1 评价指标体系构建
评价指标体系的合理构建是对方案进行有效评价的基础. 选取指标应遵循以下原则[10-11]:
1) 指标尽可能全面. 指标应能够较全面反映武器装备的性能.
2) 指标尽可能不重叠. 指标间有较多的重叠会导致结果失真, 甚至产生错误.
3) 指标易于取得. 指标有较好的可操作性, 即容易获得.
针对枪械研制初期方案评价的特点, 构建如图 1 所示的基于结构诸元的枪械评价指标体系.
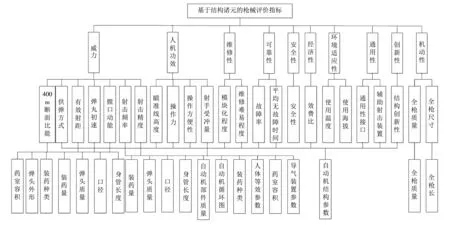
图 1 基于结构诸元的枪械方案评价指标Fig.1 Evaluation of rifle scheme based on mechanism element
1.2 指标值确定
基于结构诸元评价指标主要分为动态指标和静态指标. 动态指标主要是指与自动机运动、 人机相互作用及内、 外弹道有关的指标, 通过建立不同的数学模型进行计算获得; 静态指标主要是与枪械结构有关的指标以及暂时无法精确给出的主要指标, 可以分为定量指标和定性指标, 定量指标通过测量方案的三维结构参数获得, 定性指标则通过专家定量打分给出.
1.2.1 动态指标
1) 人-机发射动力学模型
通过建立人机发射动力学模型[12]计算得出射击频率和射手受到的冲击.
2) 自动机发射动力学模型
通过建立自动机发射动力学模型[13]计算得到自动机的速度-时间曲线, 将后坐到位和复进到位撞击能量之和的值作为射击精度.
3) 内、 外弹道模型
通过建立内、 外弹道模型[14-15]计算弹丸初速、 膛口动能、 400 m断面比能和有效射距.
1.2.2 静态指标
1) 定量指标
通过测量模型参数得到瞄准线高度、 全枪质量和全枪长.
2) 定性指标
供弹方式、 操作力、 操作方便性、 模块化程度、 维修难易程度、 故障率、 安全性、 平均无故障时间、 效费比、 使用温度、 使用海拔、 通用性设计、 辅助射击装置和结构创新性, 通过专家定性打分给出. 具体方法如表 1 所示.
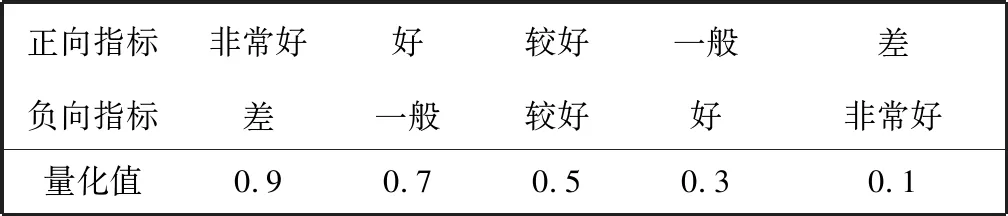
表 1 定性指标量化表
2 基于关联度的方案评价分析
2.1 熵权法
按照信息论基本原理的解释, 信息是系统有序程度的一个度量, 熵是系统无序程度的一个度量; 如果指标的信息熵越小, 该指标提供的信息量越小, 在综合评价中所起作用理当越小, 权重就应该越低. 因此, 可利用信息熵这个工具, 计算出各个指标的权重——熵权, 基本步骤如下:
2.1.1 指标初始化
枪械效能评估指标主要有3类: 正向指标, 越大越好[16]; 反向指标, 越小越好; 固定值指标, 越接近某一值越好. 为消除量纲和正负指标所带来的影响, 应该对指标值进行处理, 具体做法如下:
正向指标
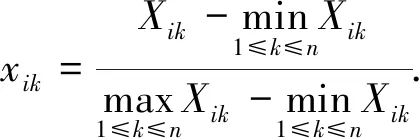
(1)
负向指标
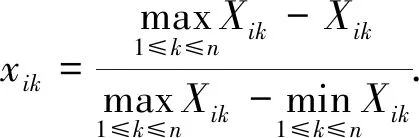
(2)
固定值指标
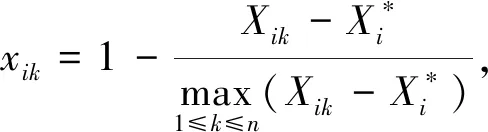
(3)
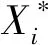
2.1.2 信息熵计算
指标值信息熵计算公式为[17]
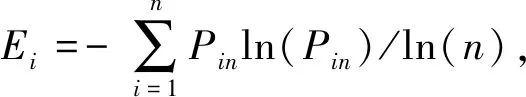
(4)
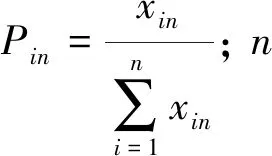
2.1.3 各指标权重确定
通过信息熵计算得到E1,E2,…,Ek, 各指标权重[17]为
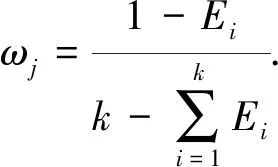
(5)
2.2 关联度分析法
关联度是灰色系统理论的一种方法 , 用来研究事物相互关联 、 相互作用的复杂因素的影响作用, 确定影响事物的本质因素, 使各种影响因素之间的“灰色”关系清晰化.
2.2.1 关联差异系数计算
先计算差异信息空间[6], 公式为
Δij=|xopt-xij|,
(6)
式中:xopt为指标值经初始化后的理想值, 值为1.
再计算关联差异系数[6], 公式为
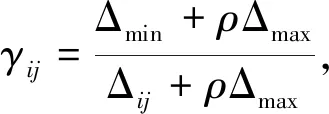
(7)
式中:ρ为分辨系数, 通常取0.5.
2.2.2 关联度计算
关联度[6]计算公式为
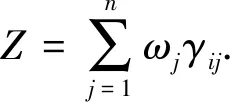
(8)
3 实例验证
3.1 验证过程
为说明本方法的有效性, 现对6款枪械方案进行评价, 具体如下:
3.1.1 指标计算
将表 2 所示的自动机参数代入自动机发射动力学模型[12]计算得到自动机的速度-时间曲线如图 2 所示.
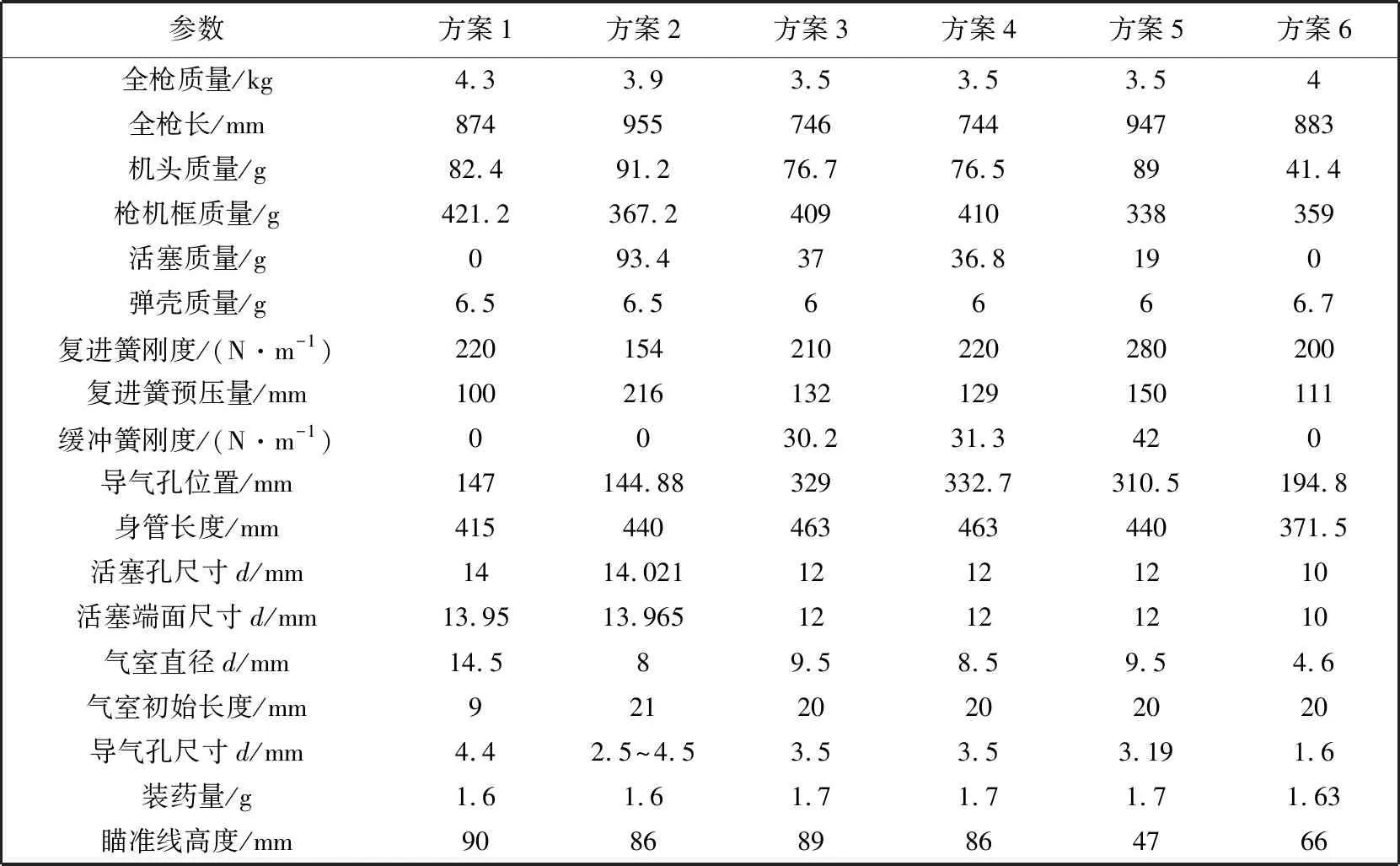
表 2 自动机参数
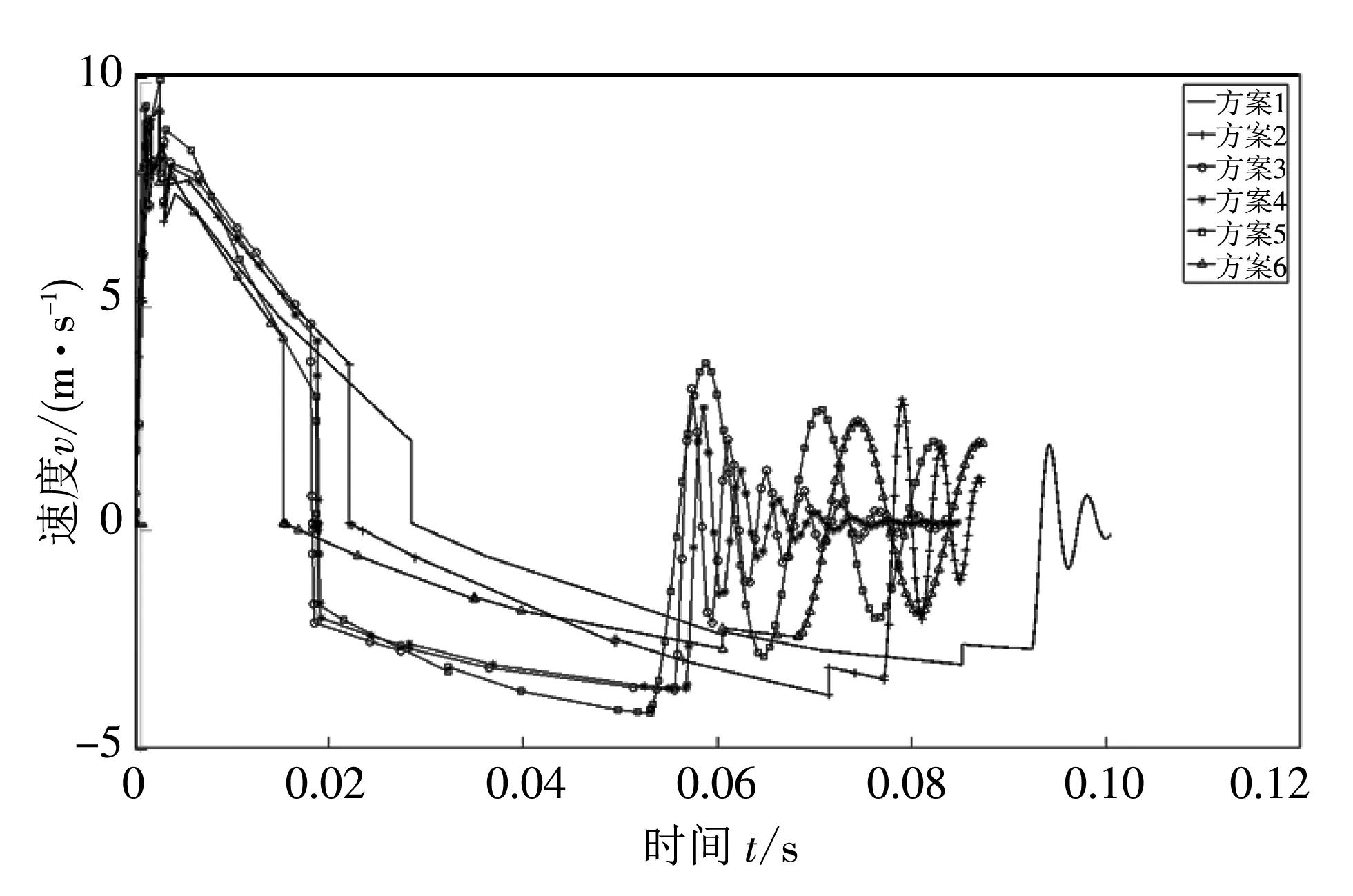
图 2 自动机速度-时间曲线Fig.2 Velocity-time curve of the automaton
将自动步枪及相关参数代入内、 外弹道模型[13-14]和人机发射动力学[11]后得到指标值如表 3 所示.
3.1.2 模型应用
步骤 1 构建评价指标矩阵
通过定性和定量方法给出所需评价指标的值, 如表 3 所示.
步骤 2 计算信息熵
将表 2 中的值代入式(4)得到指标信息熵为: (0.769 7,0.870 4,0.898 2,0.796 9,0.794 6,0.464 0,0.775 3,0.587 8,0.743 5,0.742 1,0.876 7,0.743 5,0.386 9,0.386 9,0.845 9,0,0.754 4,0.743 5,0.773 7,0,0.889 7,0.741 2).
步骤 3 计算指标熵权
将步骤2计算得到的信息熵代入式(5)得到各指标熵权为: (0.029 2,0.016 4,0.012 9,0.025 7,0.026 0,0.067 9,0.028 5,0.052 2,0.032 5,0.032 7,0.015 6,0.032 5,0.077 6,0.077 6,0.019 5,0.126 6,0.031 1,0.032 5,0.032 5,0.028 7,0.028 7,0.126 6,0.014 0,0.032 8).
步骤 4 计算差异信息空间
将表 2 中的值代入式(1), (2)后再代入式(6)得到差异信息空间如表 3 所示.
步骤 5 计算关联差异系数
将表 3 中的值代入式(7)得关联差异系数如表 4.
步骤 6 计算关联度
将表 4 中的关联差异系数代入式(8)得到各方案关联度为Z=(0.488 1,0.488 2,0.492 7,0.531 0,0.771 7,0.567 7), 6个方案关联度为0.771 7>0.567 7>0.531 0>0.492 7>0.488 2>0.488 1. 因此, 各方案的最终排序为方案5>方案6>方案4>方案3>方案2>方案1,方案5为最优方案, 方案1为最差方案.
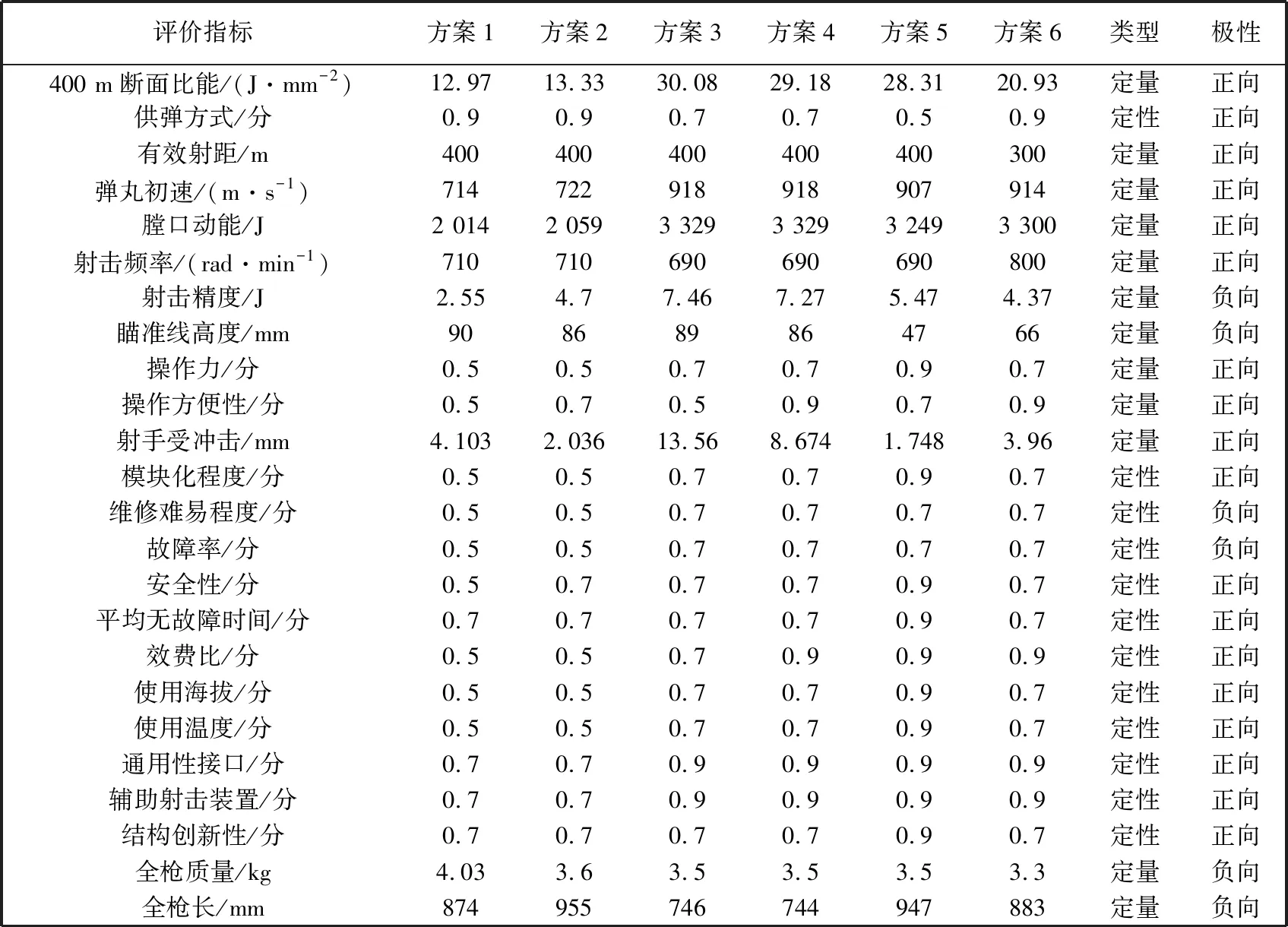
表 3 基于结构诸元方案评价指标矩阵
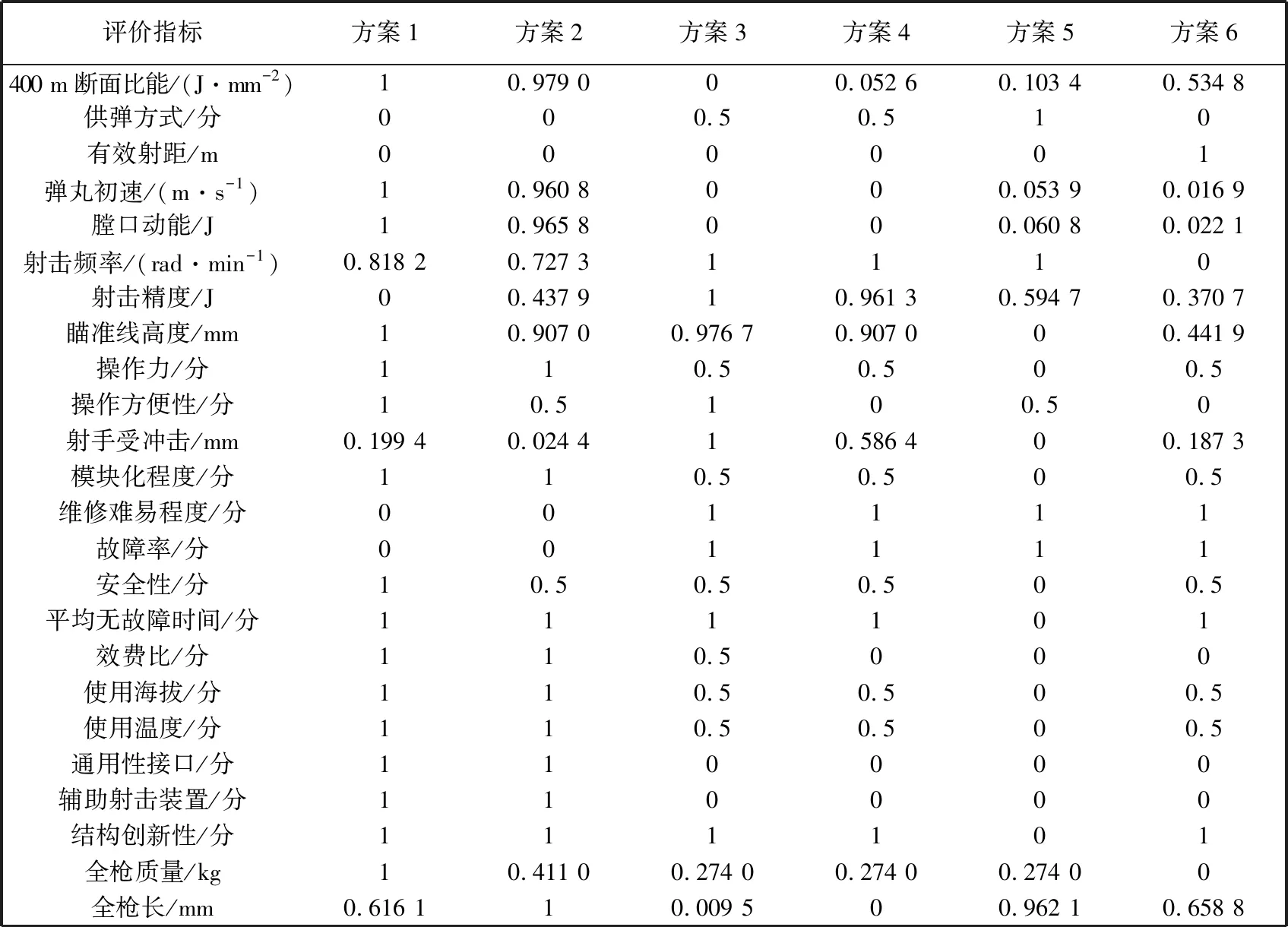
表 4 差异信息空间

表 5 关联差异系数
3.2 结果分析
以上的6个方案中方案5虽然在全枪长中排第5, 但其拥有最小的射手受冲击, 400 m断面比能、 射击精度等指标均排名较前, 因而作为最优方案较为合理.
对方案1而言, 虽然有着最低的故障率和最低维修难易程度, 但400 m断面比能、 弹丸初速、 有效射距和射击频率等指标都较差, 因此评为最差方案也是合理的.
4 结 论
本文针对枪械设计初期的方案评价主观性较强的问题, 提出了一种基于结构诸元的枪械方案客观评价方法. 以关联度分析法为评价主体, 以熵权法计算指标权重. 指标通过建立不同数学模型进行计算, 指标精度较高, 且权重通过熵权法给出, 使评价具有客观性. 该方法不仅适应于方案设计阶段, 同样适用于样机试验阶段的方案评价.
