基于2-SPR/RUPR并联机构的四足步行机器人轨迹规划与步态分析
2020-09-10马世豪李瑞琴米文博宁峰平张俊辕
马世豪, 李瑞琴, 米文博, 宁峰平, 张俊辕
(中北大学 机械工程学院, 山西 太原 030051)
自然界中的很多动物采用四足腿结构进行行走, 同时四足步行机器人也是研究最多、 应用最广的一类步行机器人[1]. 四足步行机器人通过交替地改变地面上的支撑腿来实现行走, 使其能够灵活地适应复杂崎岖地形.
并联机构驱动的布置方式极其类似于人体骨骼肌的并联布置方式, 其驱动更接近于生物. 由串并混联机构作为机械腿形成的四足步行机器人不仅具有并联机构运动精确、 承载能力大的优点, 而且能够通过串联机构放大其运动范围, 满足更大的步幅与步高[2-3]. 对四足动物腿部自由度的分析表明, 具有两转一移(2R1T)自由度的机械腿最为常见. 2R1T型机械腿可以实现步行机器人的前进、 后退、 侧行等步态[4-5].
四足步行机器人的机械腿足端轨迹规划是实现机器人移动的关键因素之一, 以实现步行机器人的稳定、 连续、 无冲击. 目前对于足端轨迹规划的方法有: 高次多项式法[6-8]、 复合摆线法[9-10]、 仿生物迈步轨迹[11-12]、 Hermite混合插值样条法[13]. 其中两段的复合摆线法求得的加速度存在抖动, 高次多项式法和插值样条法运算过程复杂, 采用三段的复合摆线法能够避免加速度的抖动且易于计算. 三角步态法[14]能够保证机器人在稳定的三角支撑下前行、 两组腿交替运动完成前行. 使用零力矩点(Zero Moment Point, ZPM)法[15-16]对四足机器人进行静态行走步态分析, 可以得到四足机器人的步态最优解.
本文结合2-SPR/RUPR并联机构[17]与平行四边形放大机构(FD)提出一种串并混联机械腿, 称为2-SPR/RUPR+FD机械腿. 对由该机械腿组成的四足步行机器人进行足端轨迹规划、 稳定性分析, 并求解最优步态.
1 2-SPR/RUPR+FD机械腿的构型
机械腿的结构对四足步行机器人的移动性能有重要影响. 2-SPR/RUPR并联机构有3个自由度(2R1T), 结合平行四边形放大机构(FD)形成串并混联机械腿2-SPR/RUPR+FD. 四个结构相同的2-SPR/RUPR+FD机械腿安装于载物平台上形成四足步行机器人. 由于平行四边形的放大作用, 可以将足端的工作空间放大, 使得机械腿有更大步幅和更高步高. 为了提高机械腿的灵活性, 利用半球形足使其与地面以点接触的方式接触.
如图 1 所示, 机械腿的驱动机构为2-SPR/RUPR并联机构, 行走机构为平行四边形机构, 驱动机构与行走机构通过球面副S连接. 在2-SPR/RUPR并联机构中, 两条相同的SPR支链和一条RUPR支链在静平台外接圆平面内相隔120°均匀布置. 初始状态下, RUPR支链所在的平面与平行四边形机构布置于同一竖直平面内. 建立足端坐标系O-xyz, 其中坐标原点O为机械腿初始位置与地面的接触点,y轴为机械腿前进方向,z轴竖直向上,x轴垂直于O-yz平面.
图 2 为使用放大机构和未使用放大机构两种情形下, 机械腿足端在O-yz平面内运动范围对比(未使用放大机构时, 取动平台中心点为足端参考点). 显然, 放大机构显著提升了机械腿的步幅与步高.
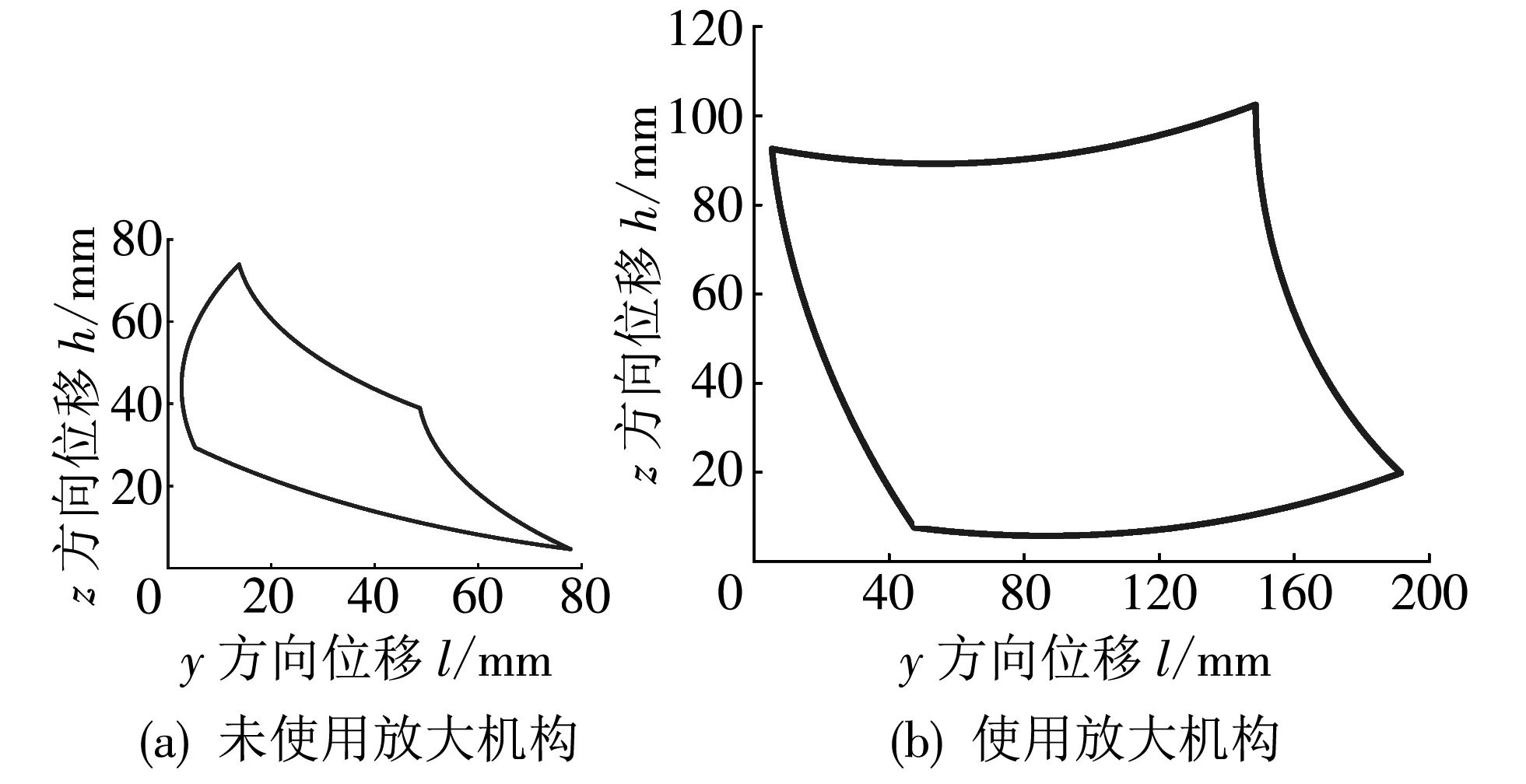
图 2 足端运动范围对比Fig.2 Comparison of foot end motion ranges
2 机械腿足端运动轨迹规划
2.1 前进运动轨迹规划
四足步行机器人在运动过程中, 其机械腿可以分为两种运动状态: 支撑腿和运动腿. 支撑腿是在单腿运动中起支撑作用的腿; 运动腿是机械腿足端离开地面并进行迈步后着地的腿. 整个运动过程中, 只有运动腿与地面存在相对位移, 因此对该运动腿进行足端轨迹规划.
为了实现平稳的运动, 机械腿足端的轨迹需要满足以下五个条件: ① 机构运行平稳, 无明显上下波动、 左摇右晃; ② 机械腿在抬腿与落腿时的加速度为0; ③ 运动轨迹速度和加速度曲线连续没有奇异点; ④ 运动轨迹曲线容易计算, 方程式简单; ⑤ 机械腿不与地面产生滑动, 无足端拖地现象.
以点O在O-yz平面内的运动为例. 运动腿的运动过程为先加速后减速的正弦运动, 设其加速度的表达式为
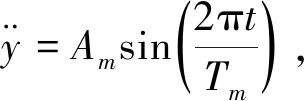
(1)
式中:Am是幅值;Tm是运动腿的摆动周期.
根据轨迹规划的要求,
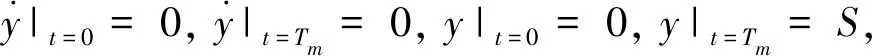
(2)
可得
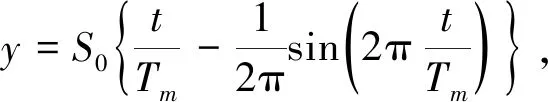
(3)
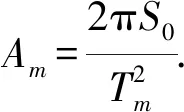
将z方向的运动轨迹分为三段, 其运动时间分别为k1Tm,k2Tm,k3Tm. 设定k1=k3=0.25,k2=0.5, 可以得到加速度的表达式为
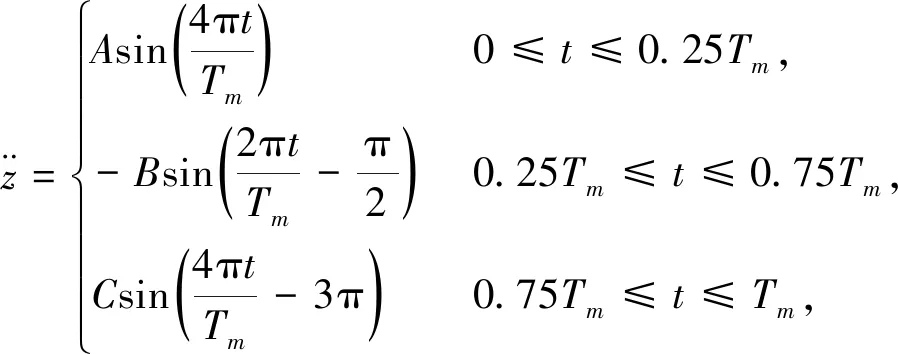
(4)
式中:A,B,C为3段正弦曲线的幅值.
对式(4)进行两次积分可以得到其对应的位移曲线方程
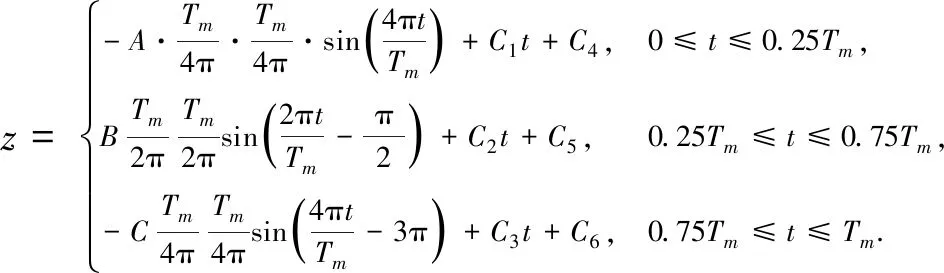
(5)
根据轨迹规划的要求, 曲线应该满足
z|t=0=0,z|t=Tm/2=H,z|t=Tm=0.
(6)
将式(6)代入式(5), 可以得到完整的位移曲线公式. 曲线方程为
z=
由式(4)和(7)得到了机械腿沿主运动方向前进的足端轨迹. 设前后运动为主运动方向, 左右摆动为次运动方向. 因为左右摆动与前后摆动, 机械腿的抬高程度都是一样的, 所以在左右摆动时, 其z方向的轨迹与前后摆动相同.
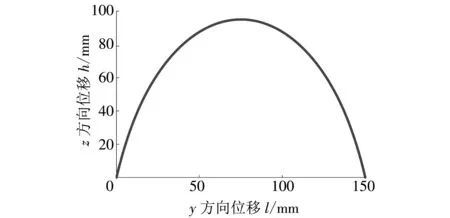
假设机械腿的初始位置为驱动副P全为伸出状态, 以O点为参考点,H=95 mm,S=150 mm, 运动周期Tm=5 s. 通过Matlab对式(1)~(7)足端轨迹曲线的函数进行一个周期的仿真, 得到的位移、 速度、 加速度曲线如图 3 所示.
(a) 足端位移曲线
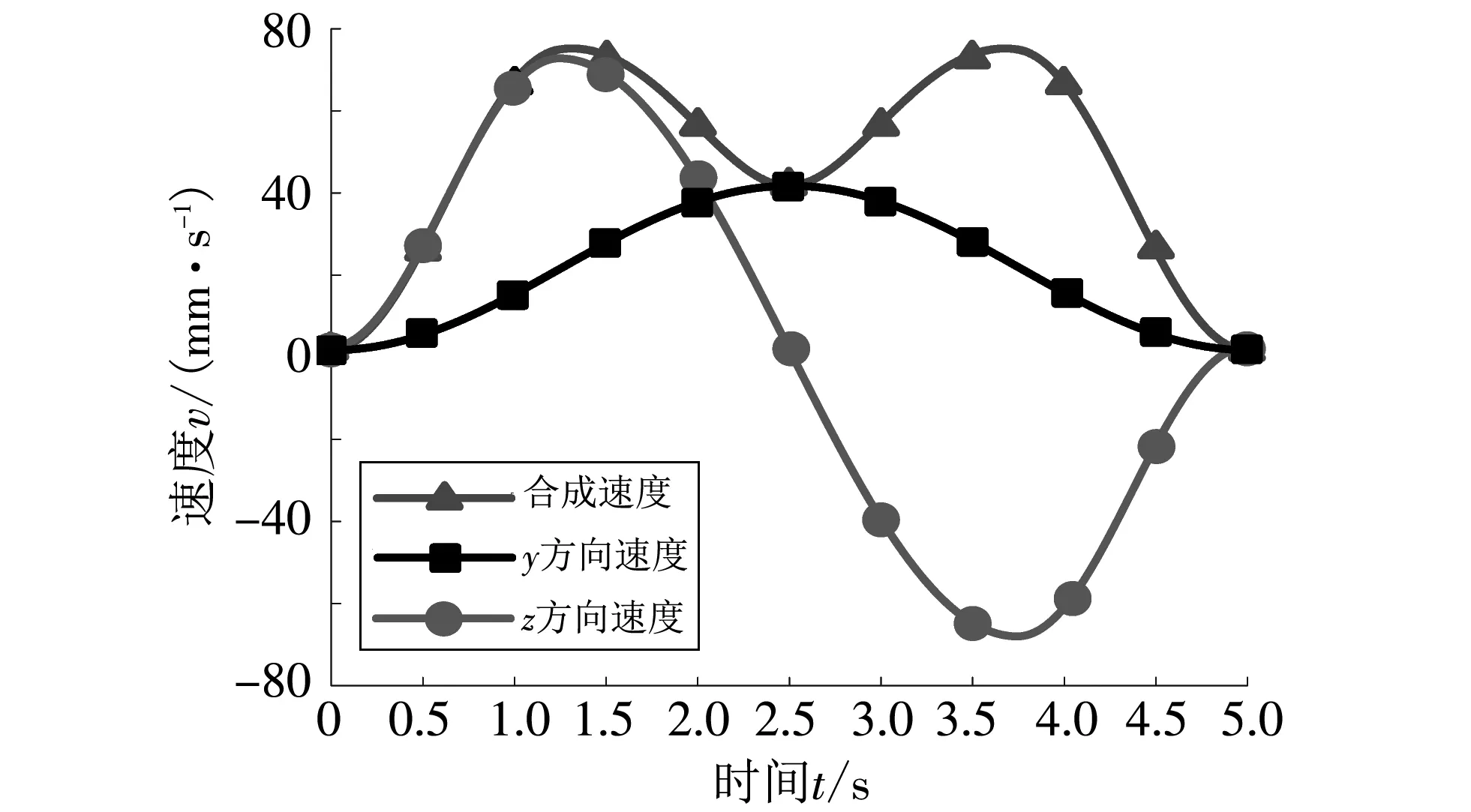
(b) 足端速度变化规律
由图 3 可知, 轨迹规划所得到的位移曲线类似于正弦曲线先抬高后落下, 满足抬腿、 着地的过程; 在整个运动过程中速度、 加速度曲线变化较为平滑, 没有尖点, 运动过程中不会出现较强的冲击从而对机械腿造成损坏, 且在开始与结束的时刻, 速度、 加速度都为0, 在抬腿与着地时刻对地面没有冲击.
3 仿真验证
将上述求得的单腿轨迹输入SolidWorks软件中进行仿真, 得到沿轨迹运动后足端的速度、 加速度曲线, 如图 4 所示.
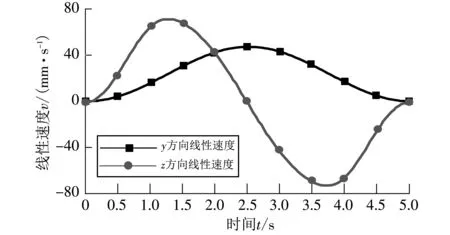
(a) y, z方向速度曲线
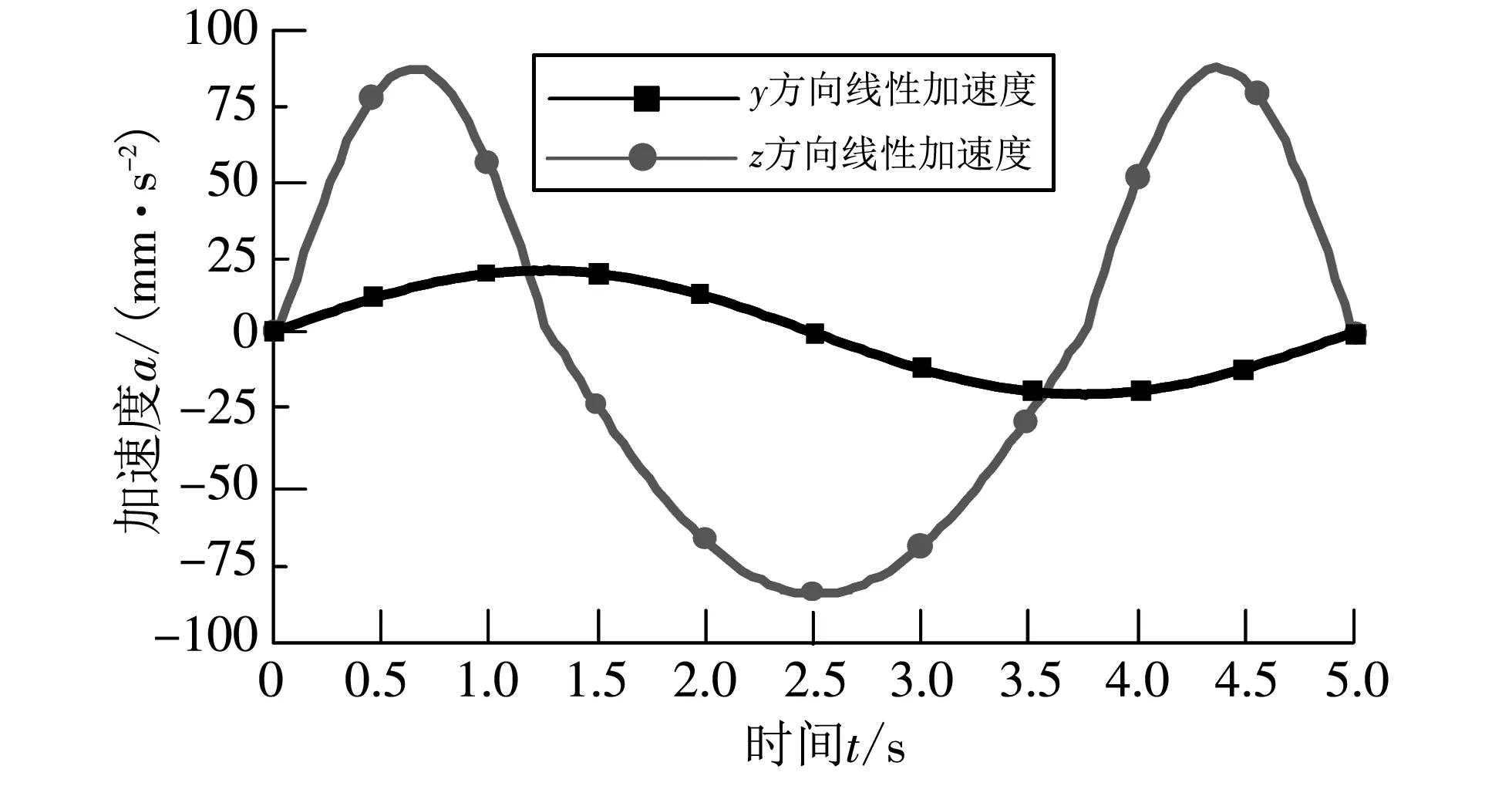
(b) y, z方向加速度曲线
从图 4 可知,y,z方向在开始与终止位置的速度、 加速度为零, 其合成速度、 加速度也为零, 能够实现机械腿在抬腿与着地时无冲击. 曲线整体较为光滑, 没有突变, 验证了机械腿运动平稳, 不会因速度、 加速度突变而导致驱动元件损坏.
通过图 5 所示曲线与图 4 所示曲线的对比发现, 理论的曲线变化图与仿真曲线变化图相同, 且曲线光滑、 无明显的突变. 通过仿真验证证明了理论计算的正确性.
4 四足机器人步态规划
如图 5 所示, 四足步行机器人的四条腿位于机体下方, 在机体上可以承载重物. 为使机器人在行走过程处于稳定状态, 需考虑以下几个问题: ① 基于并联机构的机械腿, 其质量相对较重, 因此不能忽略; ② 机器人在行走过程中机械腿的抬起与落地会引起机器人重心的偏移, 其稳定性受重心影响. 本文针对机器人行走的静态步态进行规划, ZMP法适用于水平路面以及不平坦路面, 因此采用零力矩点法作为机器人的稳定性判据.
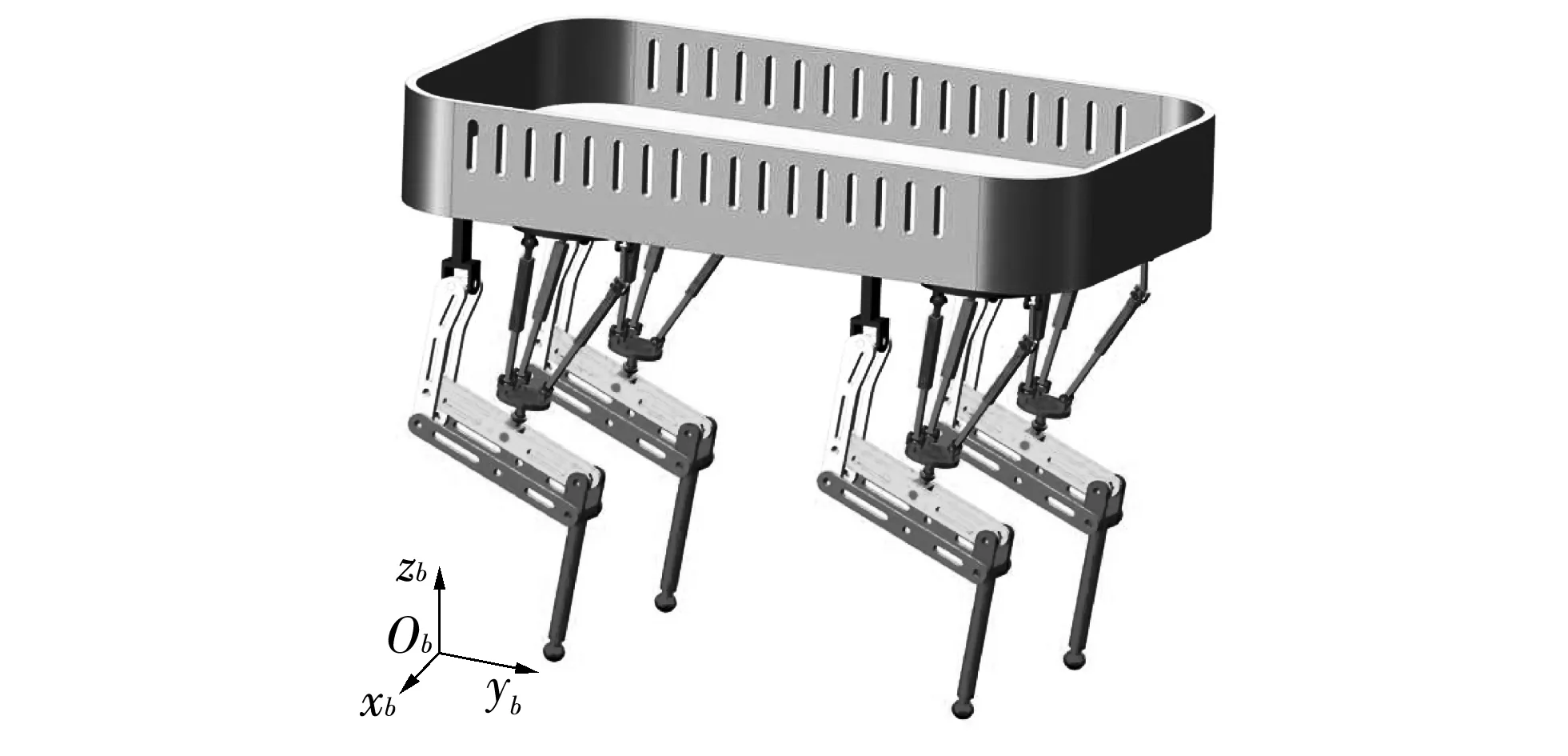
图 5 四足步行机器人Fig.5 Quadruped walking robot
4.1 稳定性判据
如图 5 所示, 建立固定坐标系Ob-xbybzb(简称{Ob}), 其中Ob位于任意位置, 坐标轴xb,yb,zb与图 1 中的坐标轴x,y,z分别平行.
设作用于第i条机械腿(i=1, 2, 3, 4)的第j个构件(j=1,2,…,9)的质心加速度为aij, 质量为mij, 质心相对于固定坐标系{Ob}的位置矢量为lij. 机器人机身的质量为md, 质心加速度为ad.
在忽略外力和外力矩的情况下, 第i条机械腿所受的合力为惯性力与重力的合力, 其表达式为
fij=mijaij+mijg.
(8)
机身所受的惯性力和重力的合力为
fd=mdad+mdg.
(9)
机器人整体所受的惯性力和重力的合力为
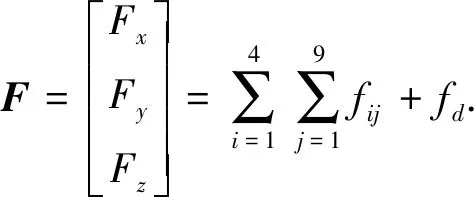
(10)
根据式(8)~(10), 可得绕固定坐标系{Ob}的坐标轴转动的力矩为
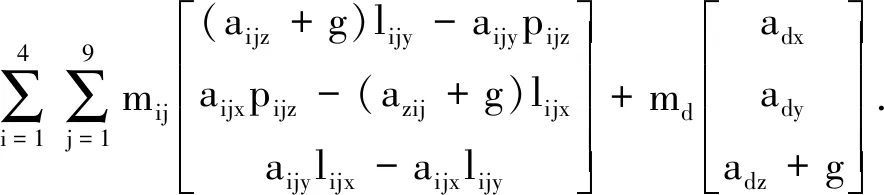
(11)
将固定坐标系{Ob}中的合力和合力矩转化到点pZMP=[xZMPyZMPzZMP], 使得该点绕xb,yb轴的力矩为0, 即
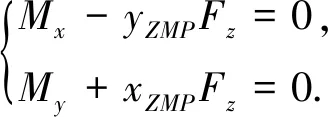
(12)
由于机器人静态步行时, 机器人速度较低, 所受的惯性力对其产生的影响可以忽略, 因此可得
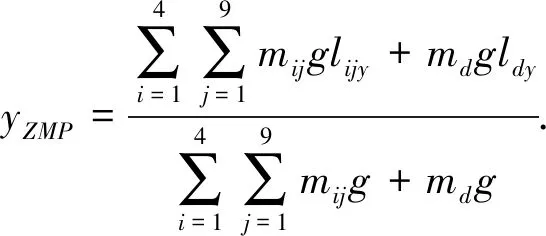
(13)
由式(13)可以得到, 当机器人静态行走时, 重心点即为其ZMP. 当机器人动态行走时, 其所受惯性力不能忽略, 重心点不是ZMP, 此时重心点可能移动到稳定区域的外部, 但要保证ZMP点在稳定区域内.
4.2 稳定裕度及步态分析
如图 6 所示, 根据机器人静态行走过程中, 足端形成的支撑三角形和ZMP的位置, 该点距离三角形各边的距离最小值为稳定裕度. 建立坐标系Og-xgyg, 其中坐标原点Og位于机身质心处, 坐标轴xg,yg与x,y方向分别平行. 设d12,d24,d14分别为点G距离三角形A1A2A4各边的距离(A1,A2,A3,A4为腿1, 2, 3, 4足端与地面的接触点), 则稳定裕度的表达式为
d=min{d12,d24,d14}.
机器人的运动过程分为机械腿的迈步过程以及机器重心的调整过程, 机械腿的迈步所需时间与其足端轨迹规划参数有关, 重心调整过程与机器人重心移动量有关, 重心移动量越小, 所消耗的时间、 能量越少. 因此, 在稳定裕度一定的情况下, 通过重心的移动量来衡量步态的优越性.
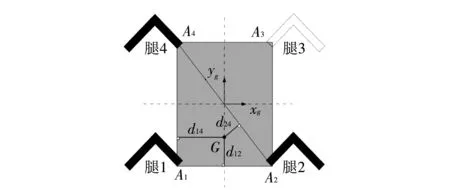
图 6 稳定裕度Fig.6 Stability margin
图 7 为四足机器人腿3或腿4先迈步时重心所进行的调整. 腿3或腿4先迈步时, 其支撑足为腿1, 2, 4或3, 重心调整方向与其运动方向相反, 该类步态不是最佳步态. 因此, 优先迈腿1或2的步态为最佳步态, 去除腿3、 腿4先迈步的步态, 剩余符合要求的有12种.
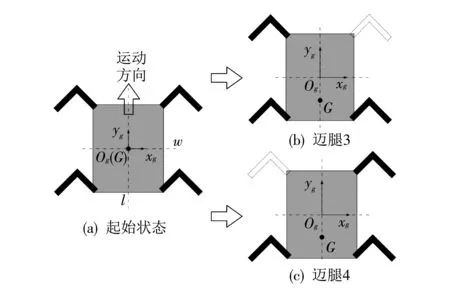
图 7 重心调整Fig.7 Center of gravity adjustment
对剩余的12种步态进行重心移动量的分析. 为了方便计算, 用重心和支撑三角形边界在前进方向上的最小距离来评价. 假设腿1到腿2的距离为l, 前腿与后腿之间的距离为w, 机械腿步幅为s. 以迈腿顺序为1-2-3-4为例分析稳定裕度和重心偏移量:
如图7(a)所示, 机器人处于初始位置, 此时的重心坐标为(0, 0), 稳定裕度为d0=w/2;
迈腿1, 重心沿前进方向移动, 坐标为(0,w/4), 稳定裕度为d1=w/4;
迈腿2, 重心继续前移, 坐标为(0,(w+s)/4), 稳定裕度为d2=(w-s)/4;
迈腿3, 重心坐标为(0,(3s+w)/4), 稳定裕度为d3=w-s/4;
迈腿4, 重心坐标为(0,(4s-w)/4), 稳定裕度为d4=w/4.
腿4落下以后机器人完成一个迈步周期, 此时的重心坐标为(0,s), 回到初始情况.
由上述分析可得, 在运动过程中, 机器人最小稳定裕度为
d=min(d0,d1,d2,d3,d4)=
(w-s)/4.
同理, 可以得到所有12种步态迈步过程中的最小稳定裕度以及重心调整量, 如表 1, 表 2 所示.
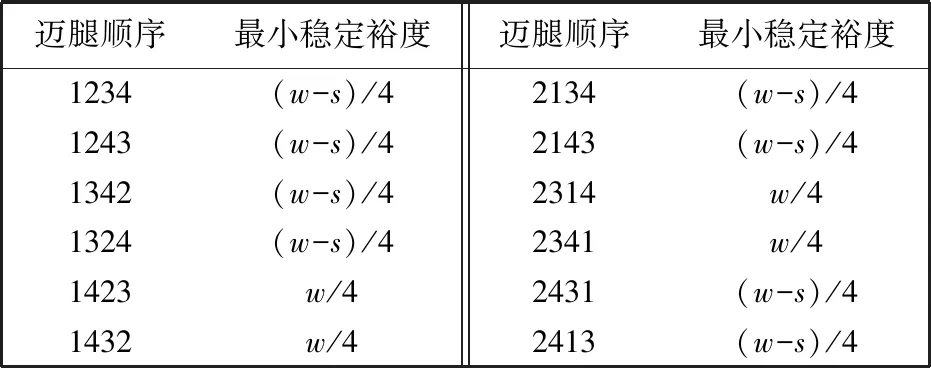
表 1 12种步态的最小稳定裕度
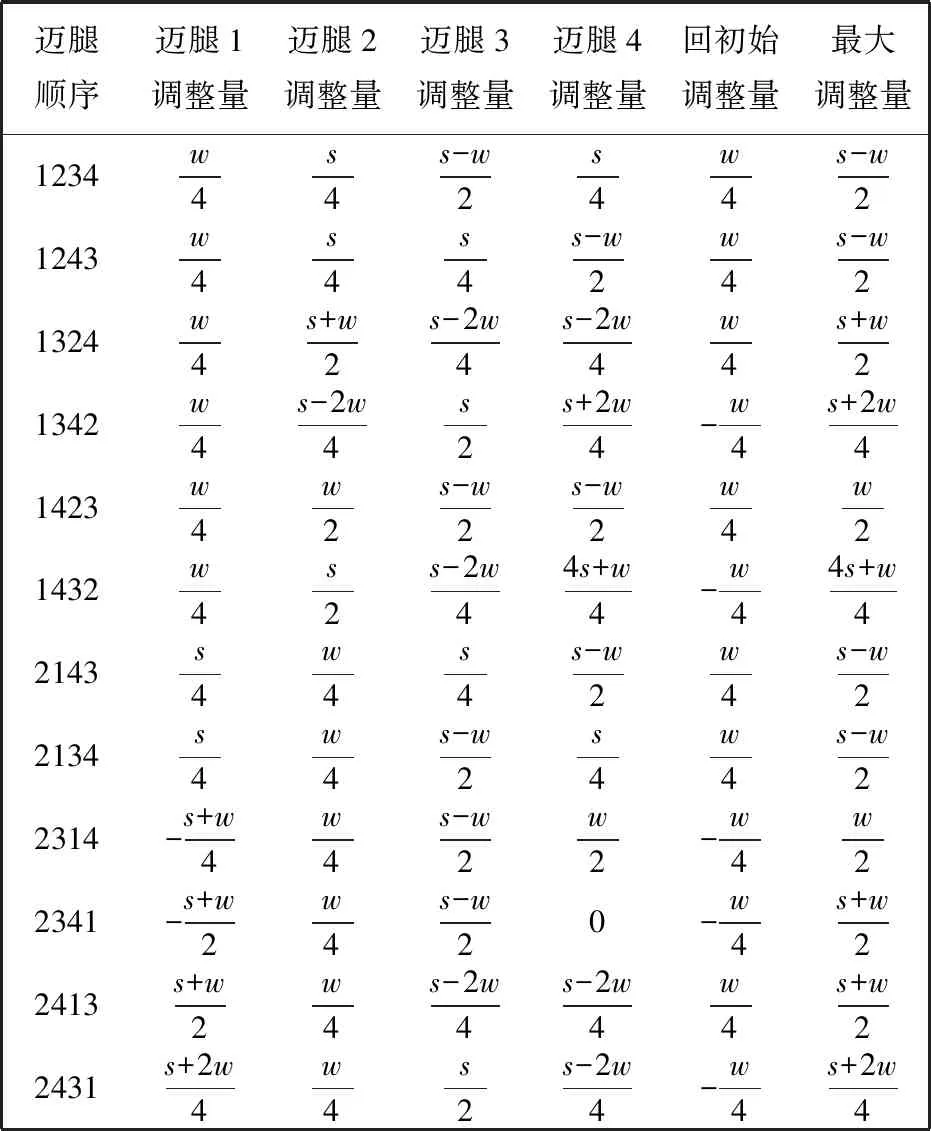
表 2 12种步态的重心调整量
因为四足机器人前后腿之间的距离为w, 且在运动过程中前后腿之间的距离必然大于其迈步的步长, 所以w>s. 通过表 2 可以得到, 以腿1和腿2为先运动的12种步态中, 步态1234、 步态1243、 步态2134、 步态2143四种步态在运动过程中重心向后调整了1次, 其余步态重心向后调整次数都大于1, 通过表1的最小稳定裕度分析可得, 这四种步态的最小稳定裕度均为(w-s)/4, 四种步态都是最优步态. 因此, 在静平衡状态行走时, 采用步态1234. 对采用步态进行三维仿真, 通过仿真能够得到机器人在对应步态下质心的变化规律.
如图 8 所示,y方向为机器人的前进方向,x方向为横向运动. 在实际应用中, 机器人存在多方面的干扰, 运动时会有偏差. 在前进过程中, 通过支撑腿对重心进行一定程度的横向调整, 即在迈左侧腿1和3时, 质心向右偏移; 在迈右侧腿2和4时, 质心向左偏移. 通过质心的左右调整, 使得其更好地落在稳定区域内, 提升了运动时的稳定性.
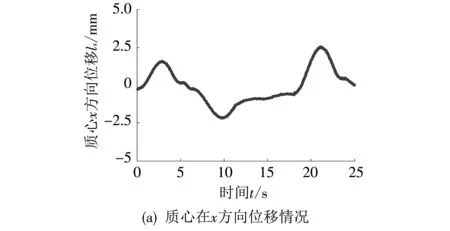
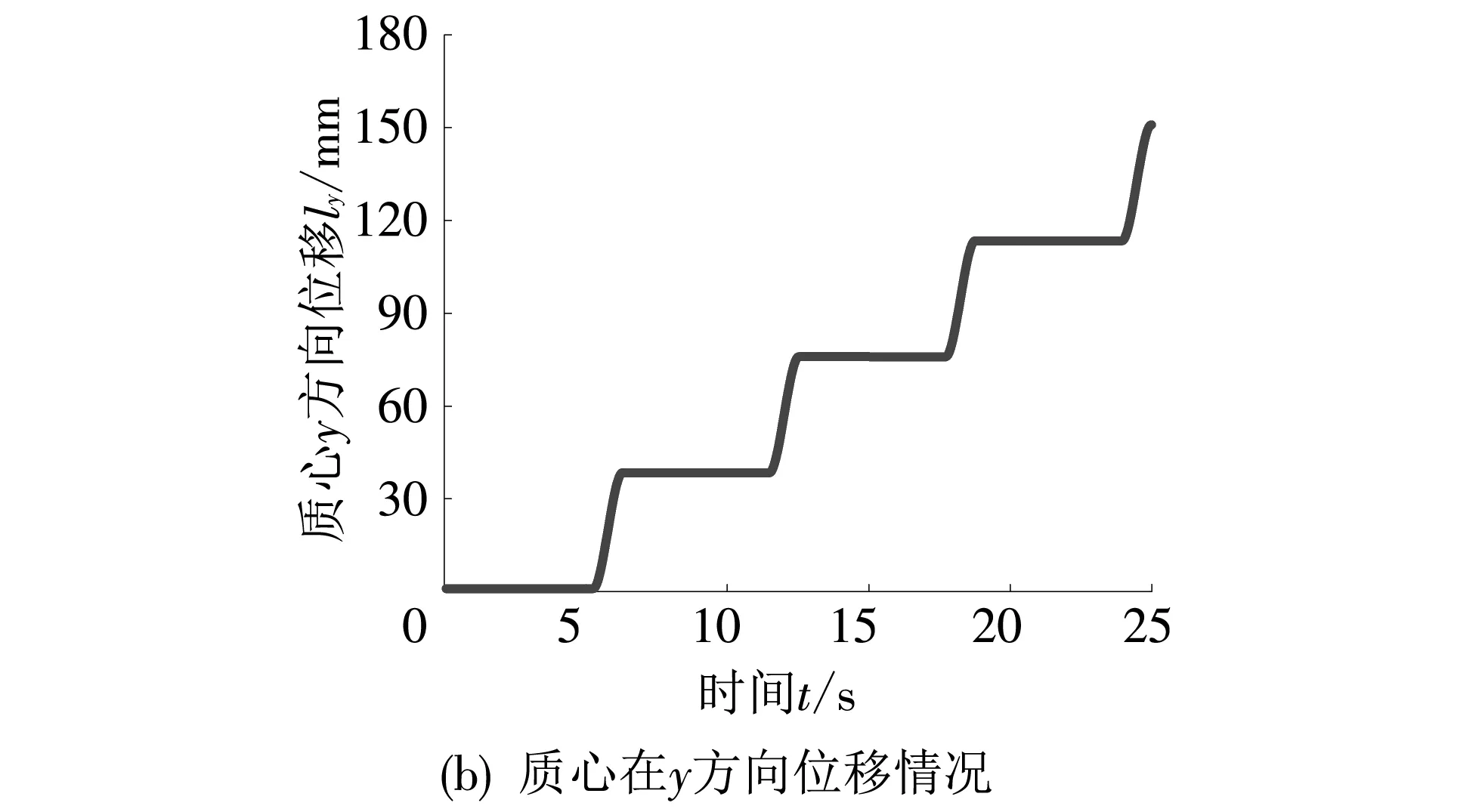
图 8 跨障时质心的变化规律Fig.8 Variation law of the centroid during obstacle crossing
5 结 论
本文提出了基于2-SPR/RUPR机构的四足步行机器人, 并对单腿结构进行了轨迹规划, 求出了轨迹曲线的函数方程及其图解. 并对该轨迹进行仿真验证, 将仿真得到的曲线与理论计算得到的曲线进行对比, 起始位置的速度、 加速度都为零, 满足设计时机械腿在抬腿与着地时没有冲击的要求, 速度、 加速度曲线平滑, 无尖点满足运动过程平稳的要求, 验证了轨迹规划的正确性. 通过ZMP方法对机器人运动过程的稳定裕度进行了分析, 使用稳定裕度值与重心调整量对比分析, 得到了静平衡状态下行走的最优步态. 四足步行机器人运动平稳且灵活, 有较大的步幅, 能够承受较大的重量. 适用于田垄、 林地等崎岖路面上需要大的移动步幅来运输重物的应用场合.
