船用双馈轴带的建模及次同步工况的仿真
2020-09-10严浪涛谭家万吴昭成刘玉生
严浪涛,谭家万,吴昭成,刘玉生
(1.重庆交通大学 航运与船舶工程学院,重庆400074;2. 美国船级社(中国)有限公司,上海 200001)
0 引 言
船用双馈式轴带发电机不同于传统的同步式轴带发电机,它具有功率因数可调、转速范围较大、变换器容量仅为转差功率的优点,适合诸如船舶主机转速因海况复杂多变而时常变化的变速恒频发电系统,比同步发电机更适合作船用轴带发电机。双馈轴带发电机的定子接电网,转子绕组通常通过双变换器提供幅值、频率、相序和相位均可调节的三相低频励磁电流[1]。
但是国内至今尚未开发出具有双馈轴带系统的船舶电站模拟器,目前有关双馈轴带的船员实操培训在基于同步式轴带系统的基础上采用口述的方式进行。当前现状使得机舱管理人员操作技术水平的更新大大滞后于现阶段船舶机电设备的更新,制约着船舶电子电气工程专业教学工作的发展。双馈轴带仿真系统的开发对推动船舶电子电气技术的发展乃至我国航运事业的发展都具有重要意义,开发双馈轴带仿真系统的必要前提条件就是对该系统进行正确的数学建模[2-3]。
1 d-q坐标系的数学模型
1.1 双馈轴带系统结构框图
根据船舶主机以及轴带发电机的工作原理,设计出双馈轴带发电系统结构图如图1所示,利用拖动螺旋的主机富裕功率,驱动双馈发电机发电。主机轴上转速会因海况和航道变化而变化,双馈发电机转子转速(图1中n)也会随之变化,使得双馈发电机工作在次同步、同步、超同步不同工作状态。为了确保双馈发电机在不同工况下定子输出电压频率恒定,该系统采用双PWM变换器实现交流励磁,变换器把电网的交流整流成直流后逆变成所需幅值、频率和相位的交流送双馈发电机转子进行励磁。
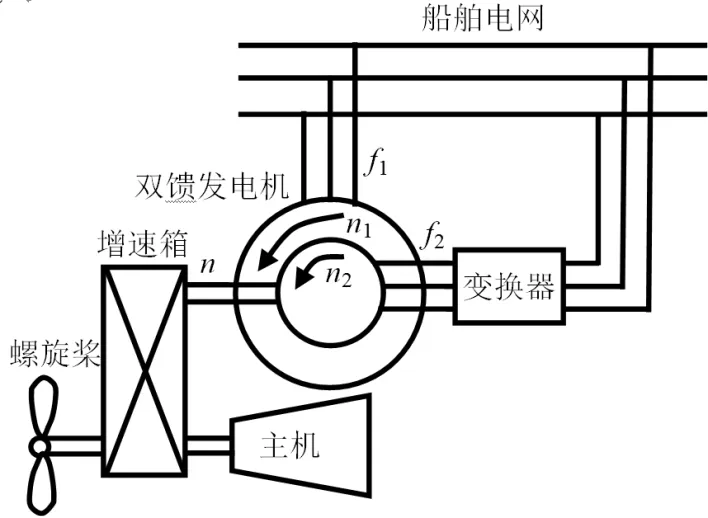
图1 双馈轴带系统结构图
设转子绕组和定子绕组均对称,其极对数p。船舶电网频率f1的电压,加到双馈发电机定子,定子绕组流过三相对称交流点产生旋转磁场的转速为n1,与极对数p的关系为
(1)
同理,变换器把频率为f2的励磁电流加到三相对称的转子绕组上,也会产生一个相对转子本身的旋转磁场,对应转速记为n2,与频率f2满足式(1)。
即:励磁电流频率f2大小决定了对应磁场的旋转速度n2[4],励磁电流的相序决定了对应磁场的旋转方向[5]。
设n1为船舶电网频率50 Hz时对应双馈轴带发电机定子旋转磁场的同步转速,要确保双馈轴带定子电压在转子不同转速下频率恒定,需同步转速n1为恒定值。
由图1的原理及式(1)得:
n1=n±n2或f1=f±f2
(2)
即,当转子转速n不等于同步转速n1时,通过调节励磁电流的频率f2(对应磁场转速n2)的大小以及调节励磁电流的相序来确保n1或者f1恒定。n与n1之间有大于、等于、小于三种不同关系,对应发电机工作在超同步、同步及次同步工况,本文只讨论次同步工况。
1.2 建模假设
在建立双馈轴带发电机数学模型前,作如下假设[6]:
(1) 定子绕组与转子绕组完全对称,且空间互为120°,磁动势呈正弦分布,忽略谐波。
(2) 忽略磁路饱和效应,绕组互感和自感均呈线性。
(3) 忽略频率和温度对定子绕组和转子绕组电阻的影响。
(4) 忽略铁损。
(5) 定子和转子相关物理量的方向采用电动机惯例。
1.3 数学模型
1.3.1 能量平衡方程
由图1可知,双馈轴带吸收能量包括两部分,一部分来自船舶主机的PSG,一部分来自变换器的PC,然后送给船舶电网。在忽略电网损耗情况下,双馈轴带发电机总的输出功率等于船舶电网所有负荷消耗的总功率[7],系统能量平衡方程如下:
(3)
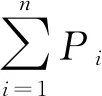
1.3.2 磁链方程
定子绕组与转子绕组在d-q坐标系[7]下的磁链方程:
(4)
式中,脚标1和2分别表示定子和转子。
1.3.3 电压方程
定子绕组与转子绕组在d-q坐标系下的电压方程:
(5)
ωs=ω1-ω2(ω1为同步角速度,ω2为转子角速度),p表示微分算子;
将式(4)带入式(5)得:
(6)
1.3.4 定子功率方程
定子有功功率与无功功率方程
(7)
设定子磁链通用表达式为
ψ1=ψmsin(ωt+α)
(8)
将该磁链的定向于d轴,则ψ1在d-q轴上的分量[8]为
(9)
在初始假设前提下,定子绕组电压:
(10)
由式(8)和式(10)得到磁链ψ1和电压u1的相位关系:u1滞后于ψ1(同d轴方向)90°,即滞后q轴正方向180°,与q轴反方向同向[8]。则电压u1在d-q轴上的分量为
(11)
把式(11)带入式(7)得:

(12)
把式(9)和式(11)带入式(5)得:
(13)
由式(4)和式(9)得定子电流在d-q轴上分量[9]:
(14)
在定子磁链定向[10]下,由式(5)得转子电压在d-q轴上分量:
(15)
把式(13)和式(14)带入式(12)得:
(16)
2 仿 真
根据上述数学模型,利用Matlab/Simulink仿真软件得到双馈轴带次同步状态的转矩、转速、电流、电压、无功功率以及有功功率的变化过程。
2.1 系统仿真模块
根据双馈轴带工作机理、转子侧变换器以及网侧变换器功能特性,在Simulink环境下搭建了如图2所示仿真模块。
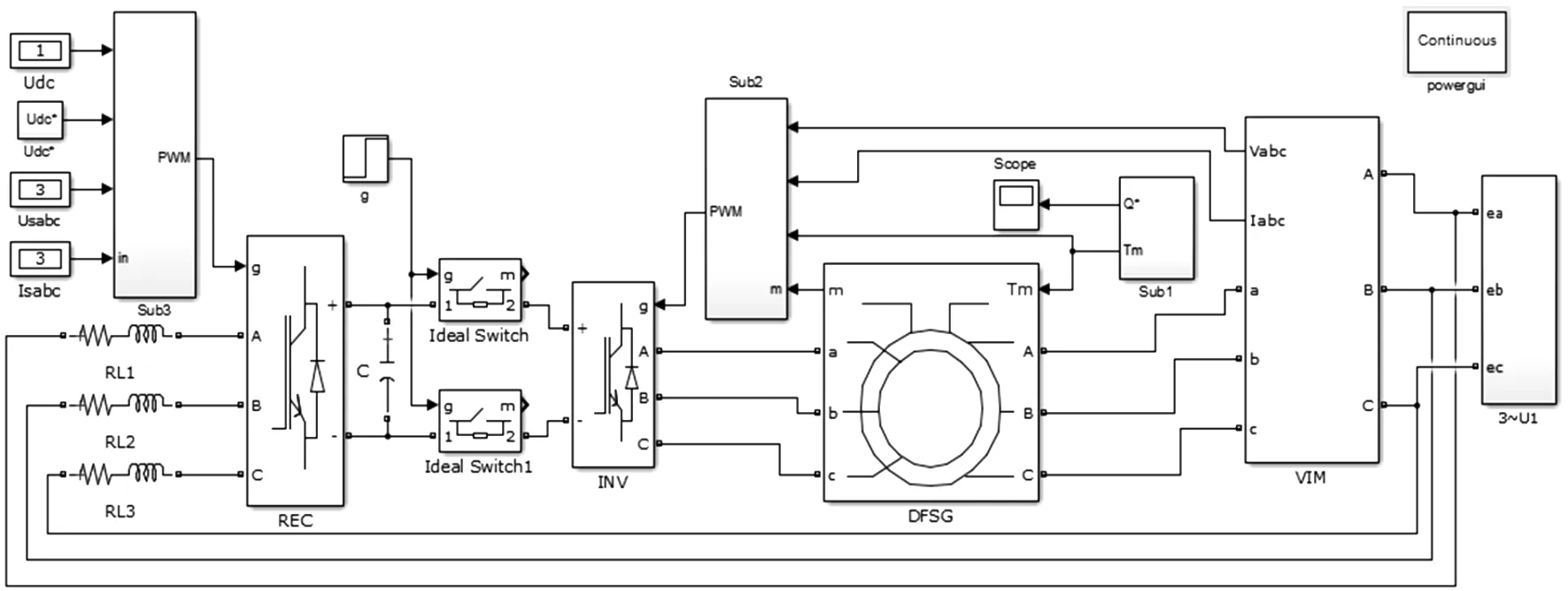
图2 次同步运行仿真模块
仿真中直流母线电压取值UDC=460V;船舶电网线电压190V(变压器变比380/190);三相对称负载(R=50Ω)星型联结;设主机转速恒定,送给轴带发电机的转矩为5Nm,使之工作于次同步状态;双馈轴带参数如表1所示。
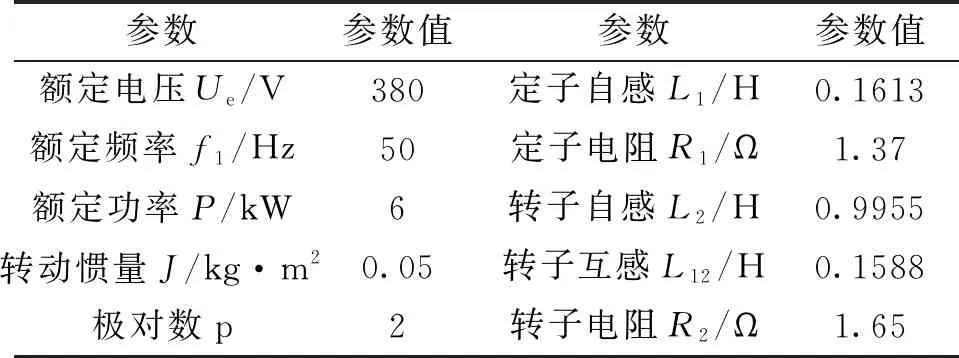
表1 双馈轴带参数
2.2 仿真波形
(1)转速
船舶海上全速稳定航行时,送给双馈轴带发电机恒定转矩,双馈轴带在该转矩拖动下起动,转速逐渐升高,对应转速波形如图3所示。1.6 s后转子转速基本稳定不变,约为1340 r/min,低于同步转速n1=1500 r/min(极对数p=2,见表1),双馈轴带工作于次同步状态。

图3 次同步转子转速
(2)转矩
船舶海上全速稳定航行时,送给双馈轴带发电机转矩恒定,对应发电机电磁转矩变化过程如图4所示。双馈轴带在t=0s收到主机拖动转矩启动,在0~1.6s的启动期间,转矩波形变化较大, 1.6s稳定后,其电磁转矩[11]约为恒值-5N·m(“-”表示与转子转速方向相反)。
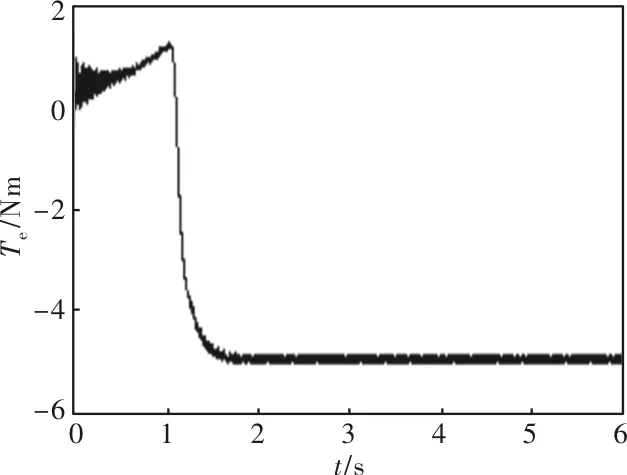
图4 次同步状态的电磁转矩
(3)转子侧变换器线电压
转子侧变换器AB两相间的线电压如图5所示,约460 V,送转子提供励磁,与双PWM中间直流母线电压设定值460 V相当。由图5可知,双馈轴带的启动阶段,即1.6 s前该电压频率大;1.6 s稳定后频率变小且基本不变,双馈轴带处于稳定的次同步状态。
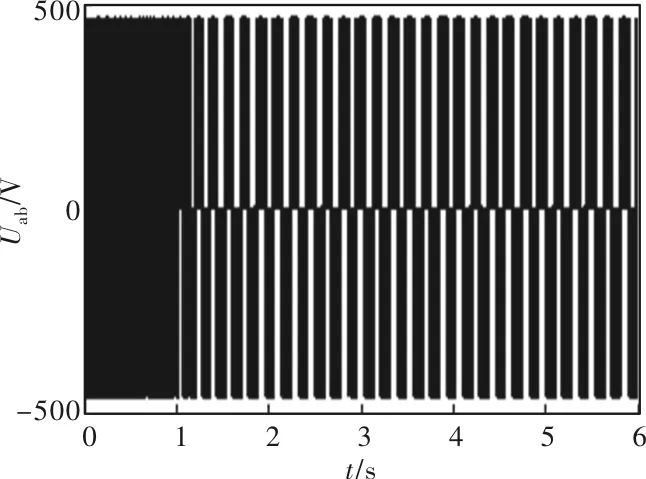
图5 转子侧变换器输出线电压
(4)转子电压与电流在d-q轴上分量
图6、图7为转子电压和电流在d-q轴上的分量,约1.6s(1.6s前为双馈轴带启动阶段)稳定。
由图6和图7可知,转子电压和转子电流在d-q轴上的分量稳定后均为恒值,无交变,频率为0。
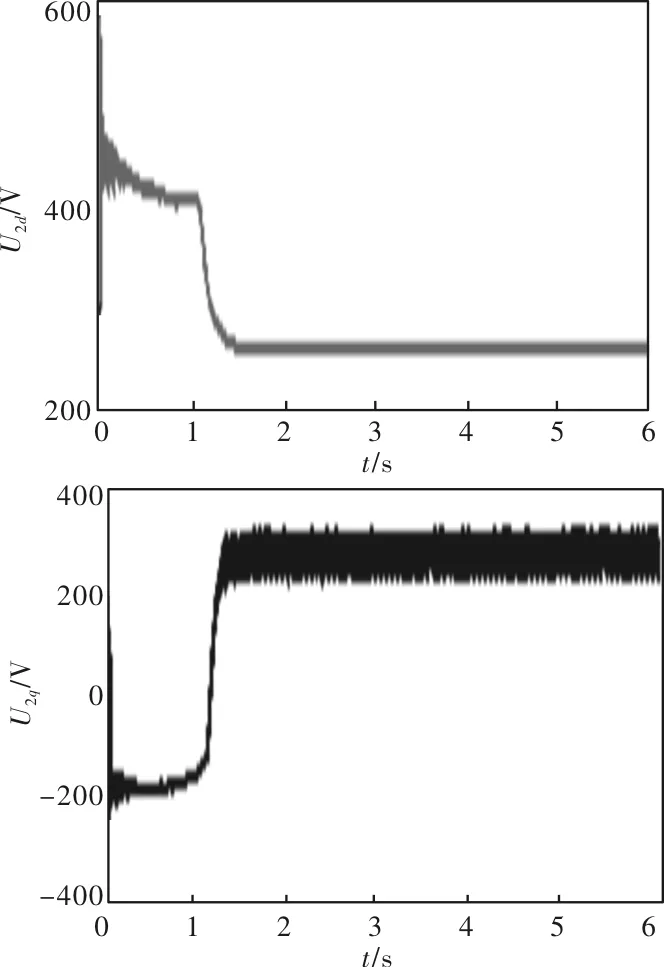
图6 转子电压d-q轴分量
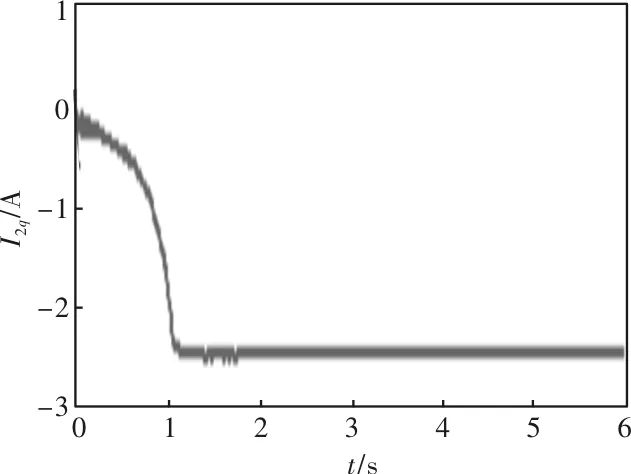

图7 转子电流d-q轴分量
(5)转子三相电流
图8(a)为转子电流A相波形图,图8(b)为转子电流ABC三相波形。双馈轴带启动1.6 s后稳定,稳定后转子励磁电流的大小、频率恒定不变。
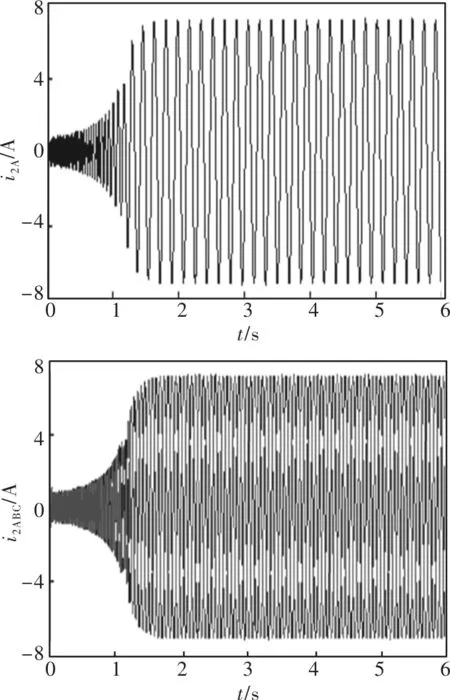
图8 次同步转子电流
(6)有功与无功
次同步状态有功与无功仿真波形如图9所示(“-”表示发电机输出功率)。无功和有功在1.6s后稳定,无功功率Q1稳定后为0Var;有功功率P1近似恒值不变,cosφ=1。
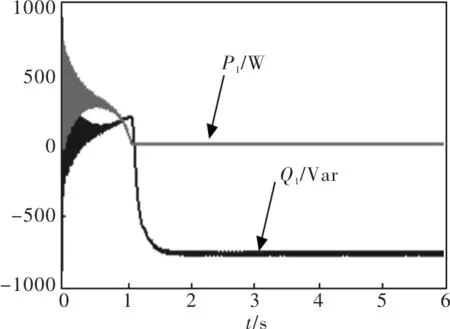
图9 次同步状态的功率
(7)定子电压与电流
为了在同一坐标下显示定子A相电流和A相电压变化趋势,电流做放大-10倍(“-”是因为建模采用电动机惯例,电流与电压反相)处理,否则因电流值太小,变化趋势不明显,波形如图10(a)所示。
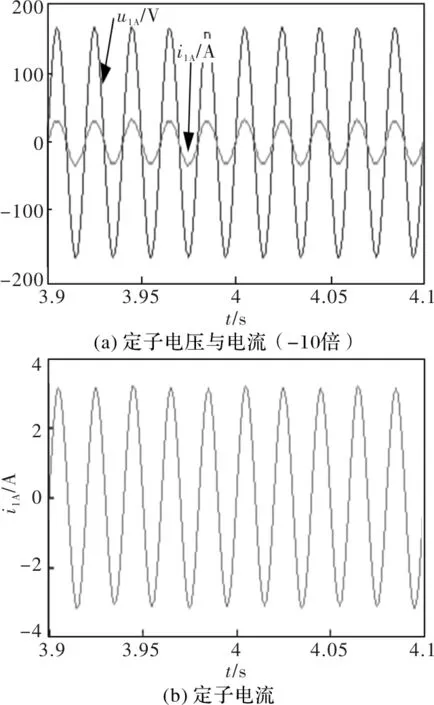
图10 次同步时定子电压与电流
从图10(a)中读出次同步时定子A相电压与A相电流的周期均为0.02 s,即频率为50 Hz。因仿真时给定负载为纯阻性负载,所以仿真结果中电压和电流应同频率、同相位,10(b)为定子A相电流。
2.3 仿真结果分析
图10(a)定子A相电压和电流同频、同相位,无功功率Q1=0与图9吻合,与仿真前提纯阻性负载吻合。由图10(b)为定子A相电流(峰值约3 A),与图10(a)定子电压(峰值约160 V)算出对应的功率;该状态负载为纯感性负载cosφ=1,计算出当前有功功率约Q1=720 W,无功功率Q1=0Var,计算结果与功率仿真波形图9吻合。由计算出的有功功率720 W,根据转速1340 r/min,在建模假设前提下可计算出转矩约5 Nm,与图4电磁转矩Te稳定后的波形一致。由图3转速波形1340 r/min计算出转子转速对应的频率为44.7 Hz,该频率与图8转子励磁电流频率(约5.5 Hz)之和为50.17 Hz(读图有误差),与定子同步转速对应频率50 Hz基本一致。
3 实 验
3.1 实验平台
实验室的双馈轴带实验平台硬件部分主要包括主电路和控制电路,主要由模拟船舶主机的变频电机、双馈发电机、变压器、变频器、背靠背双PWM变换器、电抗器、并网继电器组成,原理图如图11所示。
图11中用实验室墙上的市电模拟380 V船舶电网,送变频器驱动变频电机来模拟船舶主机,设置不同频率来模拟主机不同工况的转速,变频电机拖动双馈发电机发电,即双馈轴带。双馈发电机定子输出电压通过主开关可与船舶电网电压380 V经变压器(380/190)降压后的电能并网。同时该电压送给变换器的整流级,变换器的逆变级输出正弦交流到双馈轴带的转子进行励磁。
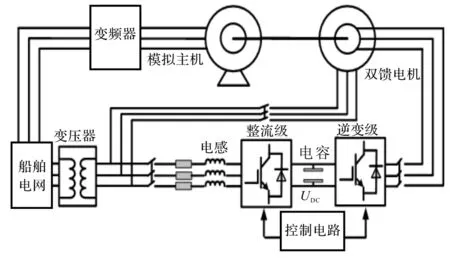
图11 实验平台原理图
实验平台硬件布置如图12所示。变频器、变频电机、双馈发电机功率分别为3.7 kW、7.5 kW、6 kW,变频电机和双馈发电机磁极对数均为2,最大转速均为1800 r/min。

图12 平台照片
3.2 实验结果
实验时,网侧变换器通电,输入电压为190 V(由实验室380 V电压经变比为380/190的变压器降压获得,如原理图11所示);该变换器投入工作进行整流,使得中间直流母线上的电压逐渐升高,最终稳定在460 V,为转子励磁做准备。
通过变频设定模拟主机的转速,拖动双馈发电机转子转动,改变变频器频率实现主机(电机模拟)转速变化。设定变频器频率使转子转速稳定在1340 r/min,此时双馈轴带工作于次同步状态;实验过程中负载为三相对称阻性负载(RL=50 Ω),星形连接。
实验结果波形如图13至图15所示。
(1)直流母线电压
稳定后的直流母线电压波形如图13所示,稳定后为460V,为提供合适的转子励磁电流奠定了基础,该实验波形与仿真波形图5的460V相吻合。
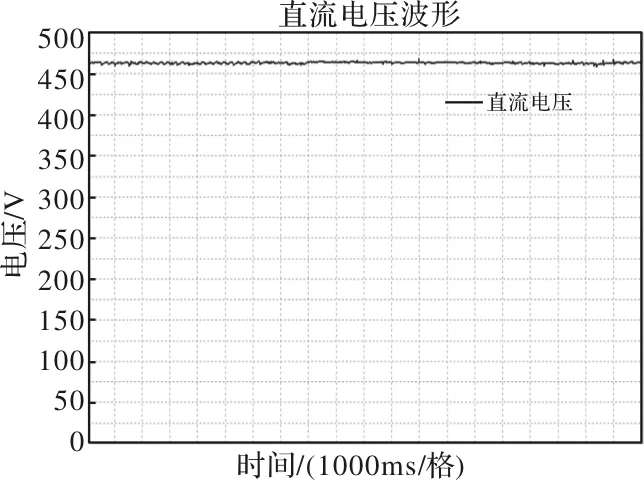
图13 直流母线电压460V
(2) 次同步转子励磁电流
次同步稳定运行时转子绕组三相电流实验波形如图14所示。
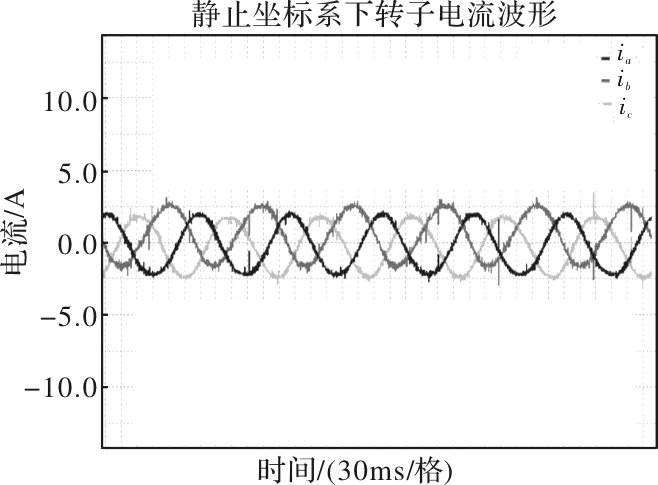
图14 次同步稳定运行时的转子电流
从图14读出次同步稳定状态下转子励磁电流的周期为
T≈300ms/格×6格=180ms=0.18s
(17)
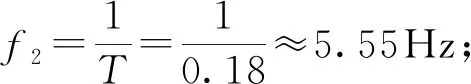
(3)定子电压和电流
定子A相电压和电流如图15所示。
为了能在同一坐标系下能看清电压和电流的变化趋势和相位关系,实验电流输出波形做了实际电流4倍放大处理。由图15可知定子电压(幅值约160 V)和电流(幅值约3 A)为同周期(T=10ms/格×2格=20ms=0.02s )、同频率的正弦交流。
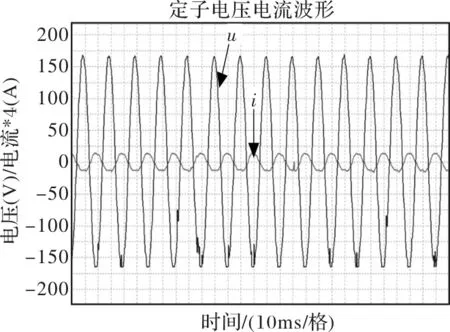
图15 定子电压与电流
图15中A相电流与电压相位相反,原因实验测量时电流方向与发电机实际电流方向相反,实际上电流波形方向为图中电流波形的反向(相位相差180°)。因此图中实际实验定子输出的电压与电流波形变化趋势和仿真波形图10定子电压电流波形一致。
3.3 实验结论
从仿真波形图与实验波形图的比较可得:
(1)仿真图中定子、转子各参数的大小、频率以及增减变化趋势和实验波形结果一致;
(2)由于建模过程中忽略了温度、频率等物理量对定、转子绕组电阻的影响,因此仿真波形结果整体上要比实验波形平滑,谐波少。
(3)上述仿真结果与实际吻合,证明了所建数学模型的正确性,有助于模拟器的开发。
4 结 语
本文针对新型船用双馈式轴带发电机进行了建模和次同步工况的仿真,仿真波形中各物理量之间的关系与实际吻合,仿真结果证明了所建数学模型的正确性,为开发船用双馈式轴带发电机的虚拟仿真系统以及故障诊断系统奠定了理论基础。
