股市网络拓扑结构与系统性风险贡献度:基于VaR风险网络模型
2020-09-09张伟平庄新田李延双
张伟平,庄新田,李延双
股市网络拓扑结构与系统性风险贡献度:基于VaR风险网络模型
张伟平,庄新田*,李延双
(东北大学 工商管理学院,辽宁 沈阳 110169)
股市的系统性风险是极端波动不断累积变化的过程,本文首次应用VaR模型构建股市风险网络,并从风险网络演化的视角研究中国股市的系统性风险贡献度,选取中国股市2008年和2015年极端波动时期,应用动态面板回归模型分析风险网络结构指标与系统性风险贡献度间的关系。结果显示:沪深股市风险网络具有无标度性;股票市场极端波动行情的出现与系统性风险的累积具有相关关系;2015年股市波动冲击比2008年金融危机冲击对风险网络的破坏更大;在股票风险网络中节点的度、接近中心性、点强度等网络结构指标与系统性风险溢出值呈显著的负相关关系,即与系统性风险贡献度正相关。为准确把握对股市的系统性风险起重要作用的机构,及防控系统性风险在整个股市网络中的传播具有重要意义。
VaR模型;风险网络;网络拓扑结构;系统性风险贡献度;极端波动
0 引言
全球化的发展使许多金融市场产生了复杂多样的关系,进而增加了金融风险的传染概率。股票之间的高度关联性为冲击波动的传染提供了可能,有些股票在这个过程中起到了冲击传染源的作用,而当这些股票系统性风险的累积达到一定值时,就会引起整个金融系统的崩盘。金融冲击波动剧烈且频繁,危机传染与股票市场的系统性风险累积有密不可分的关系,近年来众多学者把研究系统性风险的起因、累积过程和防控作为重点。单一节点发生流动性冲击,引起其他公司节点发生财务危机,从而促使整体产生系统性危机。所以计量金融网络中单一节点的系统性风险贡献度有利于把握该节点对股市网络系统性风险的重要性[1,2]。测量系统性风险贡献度常见的三种方法:一是条件在险价值CoVaR 法,Adrian和Brunnermerier[3]基于股票和债券市场数据的时间序列模型提出了条件在险价值。Girardi和Ergun[4]修改了Adrian和Brunnermerier定义的CoVaR,将一个金融机构的系统性风险贡献定义为从基准状态的CoVaR变为财务困境下的CoVaR,研究了由大量机构组成的四个金融行业集团的系统性风险贡献度,并且调查了机构特征与系统性风险贡献间的联系。刘向丽、顾舒婷[5]首次引入AR-GARCH-CoVaR模型,估算了我国房地产市场对金融系统的风险溢出效应,同时发现此风险溢出效应存在周期性。二是以资产负债表为基础的度量方法,高国华、潘英丽等[6]基于资产负债表的关联性对银行间市场双边传染风险进行研究,从信用违约和流动性风险角度对传染路径和资本损失进行估测,并深入分析银行间市场的不同结构对传染效应的影响。三是利用Copula函数计算股票市场有偏厚尾的系统性风险。除考虑金融机构自身的财务状况和相互关联情况引起的系统性风险外,还应考虑到“外部性”因素对金融部门的影响,Acharya等[7]将极端情况下的系统损失作为系统性风险的衡量标准,度量单一机构的边际成本;Krause[8]建立银行间同业拆借网络,通过外生失败的银行来触发潜在的银行危机,并分析风险在银行体系内的蔓延,发现银行体系的管理仅依赖资产负债表的规定是不够的,还必须考虑银行间网络连接的结构。研究股票网络结构拓扑指标与系统性风险贡献度之间的关系,找到对金融市场的稳定起重要作用的机构,有助于更好监督管理股市的系统性风险,并为极端波动时期防控措施的实施提供有价值的参考。
本文主要工作和贡献有三个方面:首先,基于VaR模型构造上海和深圳股市风险网络,选取研究区间包含了不同传染源引起的中国股市长期非平稳阶段,分析极端波动引起的股市系统性风险累积变化过程,探讨股市不同风险传染源引起的系统性风险溢出效应。其次,分析股市极端波动下上海、深圳股市风险网络结构的超度量空间及拓扑指标特性,说明关键股票和不同行业股票的系统性风险贡献度的变化趋势。最后,将复杂网络模型和分位数回归的CoVaR模型相结合,建立动态面板数据回归模型,分析度、点强度、接近中心性等指标对系统性风险贡献度的影响,指出股市系统性风险的整体变化趋势与复杂网络拓扑结构的关联关系。
1 文献综述
金融风险传染主要靠金融机构间的资产负债关系和信息的传播,而网络结构能更清晰地刻画金融系统内各机构相互关联的实质。近年来基于网络理论的风险传染和系统性风险贡献度的研究取得了一定的成效。
(1)基于网络节点和不同网络结构的金融风险研究。传染性是系统性风险的典型特点,而风险传染的主要载体是金融网络内部的关联度和变化规律。东南亚金融危机爆发后,有学者开始利用网络方法分析金融风险的传导过程,再加之近十几年来美国次贷危机和欧债危机的爆发,都使得人们对利用金融网络方法研究金融系统性风险和传染的危害性有了迫切需求。Iori[9]研究了在银行随机网络中节点性质的差异对网络稳定性的影响,结果表明节点异质时,银行网络的稳定性与连接程度呈现出非单调的关系,而节点同质时银行网络稳定性增强。在银行随机网络的节点差异性的基础上,考虑到银行间风险暴露程度,Marquez Diez Canedo等[10]建立了以银行为节点、以银行间的风险暴露程度为边的银行间网络,研究金融网络流动性传染过程中的变化情况。Mistrulli[11]的研究进一步表明银行间网络结构会影响风险传染过程,在完全结构网络中当违约损失率较高时,违约传染对网络结构的破坏更严重。在对节点特征和不同网络结构有了充分的研究后,学者们逐渐对整体金融系统的传染和累积产生了兴趣,Gai & Kapadia[12]构建人工同质银行网络,分析了特殊攻击对网络稳定性能力的影响,他们的研究说明金融系统具有健壮且脆弱的特点。李守伟、何建敏[13]研究了银行间市场随机网络、小世界网络和无标度网络中银行间风险传染特征及差异,发现在冲击作用下银行间无标度网络的稳定性最高。贾彦东[14]基于金融网络模型衡量系统性风险和成本分担,依次评价和分析了金融机构系统重要性模式。陈国进、马长峰[15]构建金融市场、银行系统和支付清算系统的危机传染网络模型,并对三种网络体系在金融系统中的稳定性进行了实证研究。范宏[16]建立了带有宏观经济趋势及多期清算的动态银行网络系统模型,提出了系统风险的定量计算方法,显示了系统风险的累积过程。
(2)基于网络结构特征和系统性风险贡献度的关系。网络结构在维持系统稳定性上起重要作用,巴曙松等[17]研究了风险传染过程中网络结构的作用,并在金融网络结构层面提出了关于增强金融市场稳定性的措施。高波、任若恩[18]构建了金融系统的Granger因果关系网络模型,分析了在不同市场状态下各金融部门间因果关系的网络结构特征。在了解网络结构维持系统稳定性有重要作用的基础上,可深入探究网络内部关联性与风险传染、网络结构与系统性风险贡献度间的关系,如:为了分析我国银行网络的系统性风险,范小云等[19]使用DAC和CCA方法得出居于风险传染网络中心的银行节点的系统重要性更高。隋聪等[20]构建银行间网络,发现网络集中度与风险传染可能性之间存在显著的正相关关系。邓超、陈学军[21]基于多主体建模分析了银行间核心—边缘网络的系统性风险,发现核心—边缘银行网络系统比无标度网络更易遭受共同冲击和传染风险,但当处于金融困境时,该网络体系又比其他网络结构表现出更强的恢复力。王占浩、郭菊娥等[22]在银行间资产负债关联基础上,引入资产价格传染渠道,构建银行间风险传染模型,表明资产价格关联是银行间风险传染的重要渠道,应作为系统性重要机构评定的重要参考。Huang、Stan Uryasev等[23]建立了中国金融机构网络,运用CoVaR方法和DCC-GARCH模型分析了局部拓扑网络和系统性风险贡献度之间的定量关系。近年来,一些学者将风险传染的传染源和传染渠道引入仿真网络模型来分析网络结构特征和系统性风险传染的关系,Niko Paltalidis等[24]采用最大熵方法构建欧洲金融网络,使用系统性风险的三个传染源模拟传染冲击,结果发现欧元区北部银行体系的系统性风险不太明显,而南部银行体系却更容易受到金融危机引发的倒闭银行的影响。隋聪、谭照林等[25]提出了基于网络模型的银行系统性风险的度量方法,发现银行网络潜在的传染性显著放大了银行系统的风险,而且违约传染效应呈现出指数增长。邓向荣、曹红[26]应用格兰杰因果检验和空间方法建立了中国金融风险传染网络模型,研究系统性风险爆发后的风险传染路径,并通过网络拓扑指标评价各金融机构风险网络传染的速度、范围及深度。
综上发现,已有文献研究金融市场网络时多采用价格波动关联的建模方法,且应用网络模型的系统性风险研究多集中在银行网络和金融机构网络,探究不同网络结构对系统性风险的影响。部分文献仅关注股市波动影响下的银行间网络结构变化,但忽略了不同传染源引起的股市波动下长时间区间内股市网络结构的演化过程是否会出现差异,以及不同行业股票在不同传染源引起的股市波动的主导性强弱变化,不能反映股票市场系统性风险的整体变化趋势。在此基础上,本文注意到股票市场是一个高风险市场,股票价格的大幅波动,如2008年和2015年的股灾都是股价在某时点突然崩盘[27],在短时间内给投资者造成了巨大损失,反映了股票价格波动系数不能够准确的刻画股价间的长期均衡关系,因此本文以VaR模型为基础构建风险网络模型,因为VaR模型提供了衡量市场风险的有效方法,并且VaR数组的相关系数反映了股票间的风险相关性[28],这为研究股票网络的系统性风险、风险传染和网络稳定性等提供了一个新的视角。
2 系统性风险贡献度
从金融网络角度看,网络中每个节点都具有系统重要性,只是重要的程度有所差异。系统性风险贡献度是指特定金融机构在风险压力条件下整个系统的在险价值(CoVaR),并将CoVaR减去非风险压力下整个系统的VaR值作为该金融机构对整体金融系统风险的边际贡献,并以此衡量该机构的系统重要性水平[29]。
2.1 CoVAR模型



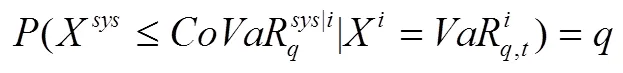
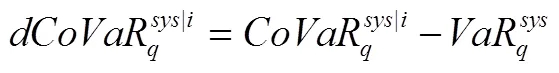
2.2 分位数回归法求CoVaR
目前有3种测量CoVaR的方法:分位数回归法、GARCH模型法和Copula函数法。因分位数回归法对分布的假设要求不高,能更加准确地刻画分布的尾部特征,也适用于含有异方差的模型,可有效弥补其他回归方法在这点上的缺陷。本文借鉴Adrian和Brunnermeier[30]的做法,构建如下单支股票的分位数回归模型:
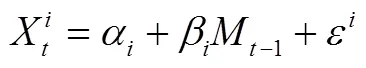
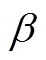
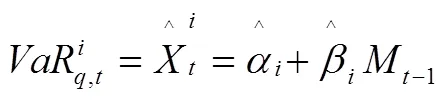
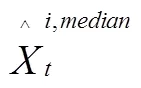

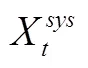
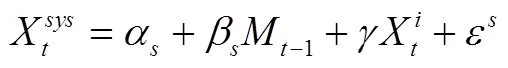
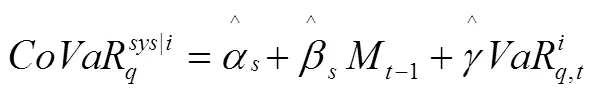
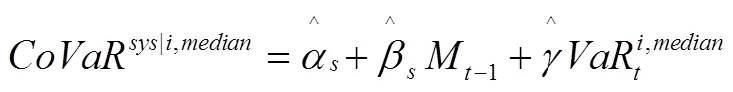
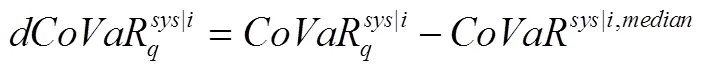
将式(8)、(9)代入式(10)整理后可得:
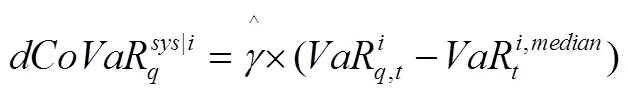
3 模型构建
3.1 股市风险网络
3.1.1风险网络的构建
Jorion[31]给出风险价值VaR的权威定义为“给定置信水平下,某一资产或投资组合在未来持有期内的最坏的预期损失”。运用VaR模型构造股票网络,是利用VaR能预测资产组合的潜在风险的特点,计算VaR数组的相关系数,并用最小生成树方法(MST)构造风险网络。具体步骤如下:
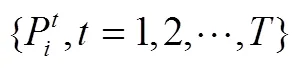
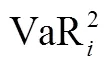
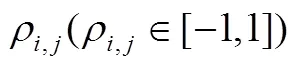

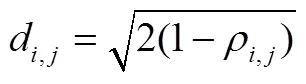
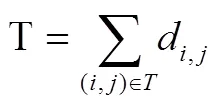
3.1.2网络结构指标
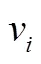
(2)点强度()。根据已有文献,点强度的定义是与节点相连的所有连边的权重的总和。
(3)接近中心性()。它表示网络中某节点的连接能力,反映了节点在网络中居于中心的程度。节点接近中心性值的大小,表明它与其他的节点(公司)连接的远近,若某节点接近中心性越大说明其越居于网络的中心位置。
3.2 dCoVaR与网络拓扑指标的动态面板回归模型
为了研究股票市场网络拓扑结构对股票市场系统性风险贡献度的影响,建立动态面板数据回归模型。选取面板数据:因变量是单个股票的dCoVaR,自变量是网络结构指标。鉴于已有研究发现单个股票公司规模大小、资产负债比率、盈利能力等显著影响了公司的系统性风险贡献度,本文也选用这些变量为自变量。
在进行回归前为避免虚假回归,要检验面板数据是否存在单位根,以检验数据的平稳性,确保估计的有效性。单位根检验方法较多,为方便,本文采用不同单位根检验的Fisher-ADF检验方法,如果拒绝存在单位根的原假设,就认为此序列是平稳的。我们采用Hausman检验来判断是选用随机效应模型还是固定效应模型,给出的零假设是:建立随机效应模型。如下:
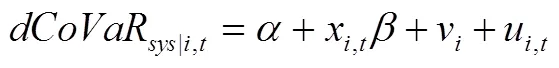
4 实证检验
4.1 样本和指标数据的选取
研究样本为我国上证180指数成分股和深证300指数成分股,剔除受到上市日期影响、连续停盘超过24天和公司财务数据不齐全的股票,最后分别得到89支、83支股票。选取股指极端波动鲜明的两大时间段为研究对象,分别是2008年金融危机前后和2015年股市暴涨暴跌前后(简记为“样本区间1”和“样本区间2”),在整体研究的基础上,根据股票收益率波动强度大小,将波动时段最高的2007-12-03至2009-6-30与2014-10-10至2015-06-15划分为“波动时期”,选取2006-06-02至2007-11-30和2013-10-10至2014-09-30为“波动前”,2009-07-01至2010-12-30与2015-10-08至2016-12-31为“波动后”。
分位数回归模型中:参考已有文献[35],分别选取上证综指和深证综指收益率作为状态变量,选取沪深300指数收益率作为系统指标。动态面板回归模型中:除了选取股票网络拓扑结构指标节点度、接近中心性、点强度之外,还考虑系统性风险贡献度的其他影响因素,如:公司的盈利指标(ROA)、公司的规模大小(Assets)、公司的负债指标(Leverage)等。
4.2 股市系统性风险贡献度的静态分析
根据式(10)计算在时,上海和深圳股票市场两个样本区间内单只股票对整个股票市场的系统性风险的边际贡献度dCoVaR,如图1所示(此处对dCoVaR取绝对值处理)。
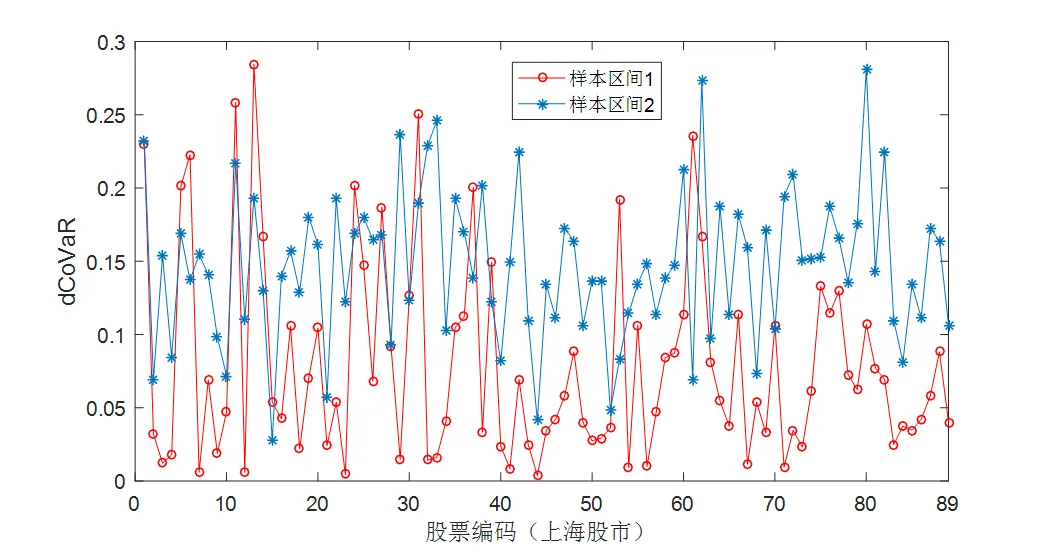
Figure 1 The dCoVaR of each shares in Shanghai and Shenzhen stock markets
注:将公司股票代码按升序排列后从1到n依次编码。
观察图1发现在分位数时,上海股市dCoVaR的趋势线要大于深圳股市的dCoVaR趋势线,说明上海股市系统性风险的累积程度要远大于深圳股市系统性风险的累积程度,即当在极端行情发生时上海股市比深圳股市更容易爆发危机。上下两幅图从总体上均呈现出样本区间2股票的dCoVaR曲线在样本区间1的dCoVaR曲线之上,说明在2015年国内股市剧烈震荡阶段无论是上海还是深圳股票市场的系统性风险累积量都大于2008年国际股市危机阶段。从单一股票角度,两个股票市场中各个股票的dCoVaR值在0到0.3的范围内波动,说明不同股票所代表的公司机构对整体的系统性风险贡献存在较大的差别。两个样本区间内均有某些股票节点的dCoVaR值大于0.2,说明风险发生时,这些股票对股市整体的系统性风险产生的影响较大,而上海股市和深圳股市甚至有个别股票的dCoVaR小于0.01,说明这些股票节点代表的公司尽管其处于风险状态时,也不会对整个股票市场系统性风险产生较大的影响。
4.3 股市系统性风险贡献度的动态分析
为更清楚的观察单只股票的dCoVaR变化,分别选取两个样本区间内都有且dCoVaR排名比较靠前的浦发银行和西山煤电两只股票,图2、图3给出两只股票dCoVaR的动态演化图像(由于篇幅限制不能逐一给出每只股票的dCoVaR的动态演化图像)。
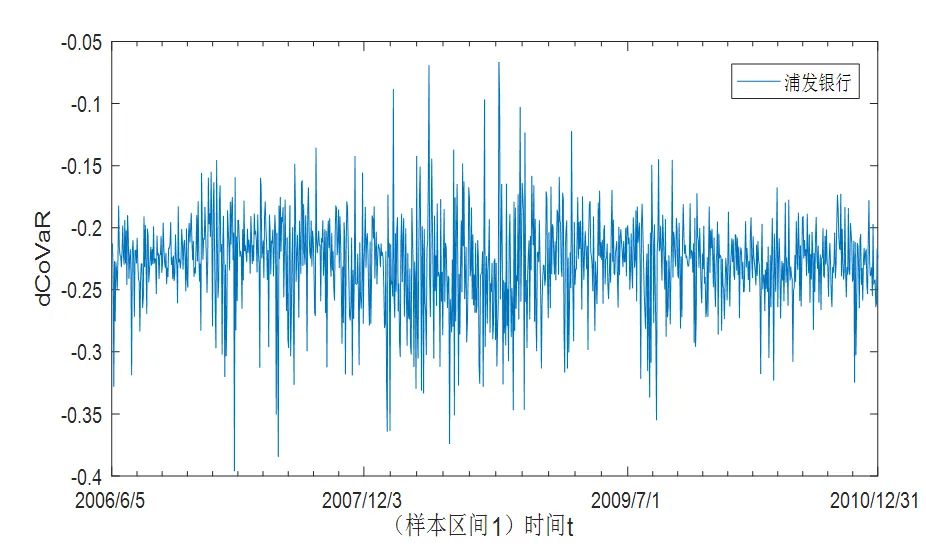
Figure 2 The dynamic evolution of pufa bank's(Shanghai)

Figure 3 The dynamic evolution of xishan coal and electricity company's(Shenzhen)
根据定义知:dCoVaR的值为负且值越小时说明单个股票对系统的风险贡献度就越大。由图2、图3发现浦发银行和西山煤电两只股票dCoVaR的剧烈震动都发生在2007年底~2009年6月、2013年底~2015年9月(极端波动期),在这一时期dCoVaR出现局部最小值的几率更大,而在2010年底和2016年底(波动结束)dCoVaR的波动趋于平稳。浦发银行dCoVaR均值在两个样本区间内分别趋近于-0.224和-0.230,西山煤电dCoVaR均值分别趋近于-0.089和-0.175 。显然样本区间2股票的系统性风险溢出值大于样本区间1,同样证明了静态分析时认为的2015年股市剧烈震荡期间股票系统性风险累积量大于2008年国际金融危机时期的结论,致使2015年由于国内股市自身结构调整爆发的股市震动破坏性更强。从两幅图看出单个股票的dCoVaR出现剧烈波动且振幅很大时,股市也恰好出现了极端波动,暗示股市的极端波动与系统性风险的累积有关系。系统性风险的不断累积使风险溢出值达到最小时,单个股票对股市系统的边际风险贡献度更大,微小的增加值很可能会导致整个股市危机的爆发。此外,从图像的整体震动幅度来看,无论是浦发银行还是西山煤电,其在2008年金融危机时期的dCoVaR的总体震动幅度与2015年股市震荡时期的总体震动幅度都存在显著差异,进一步说明了相同股票在不同时期因风险传染源的不同,其系统性风险溢出值不同,即该股票对整个股票市场的风险贡献度不同。
4.4 MST股票风险网络结构
(1)MST图
基于VaR模型构建股市风险网络时,时间跨度选100个交易日。用Kruskal算法将距离矩阵转换为使式(14)值达到最小的超度量关联网络的子网络。给出两个样本区间内上海、深圳股市MST风险网络的节点间联通性、位置的变化图。如图4、图5。
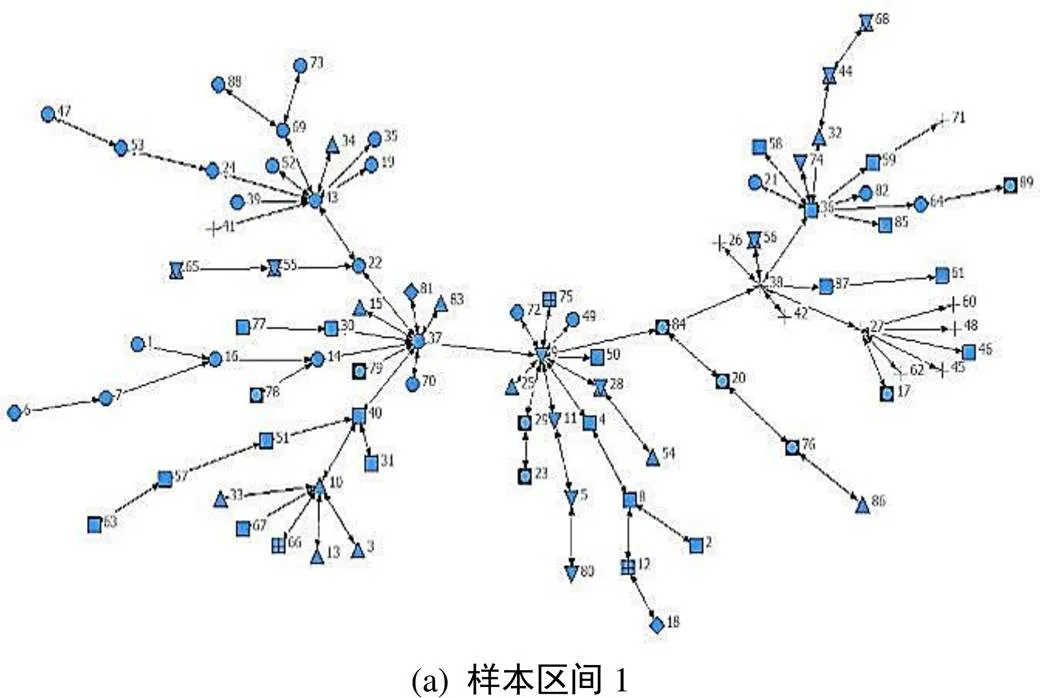
Figure 4 Shanghai stock market MST network diagram in two samples
图4(a)中上海股票MST网络中有七个关键节点:上海电力(11条连边),雅戈尔(10条连边),北京城建、复星医药和巨化股份(9条连边),同仁堂(7条连边),中海发展(6条连边),从图中看出在MST风险网络中连接节点最多的集中在金融行业,说明金融业在上海股市受到极高的关注度;图4(b)中上海网络的连通性一般,其中东方电气(11条连边),华夏银行、江西铜业、国电电力(5条连边),上述连通性较好的节点为上海风险网络中的重要节点。上海MST图4(b)中关键节点的个数明显小于图4(a)MST中关键节点个数,说明样本区间2该时间段内上海股票市场网络结构遭到剧烈破坏,连通性及关键节点数目显著下将。图5(a)深圳风险网络中有4个重要的节点:银河生物公司(14条连边),分众传媒(9条连边),北新建材(5条连边)等;图5(b)中起重要连通性作用的节点有:海王生物和深圳能源(9条连边),兴蓉环境等(6条连边)、大族激光(5条连边),显然样本区间2深圳风险网络的连通性和关键节点数目也显著下降,同样证明2015年国内股市震荡对深圳网络结构的破坏性远大于2008年国际金融危机的破坏性。深圳MST网络在两个样本区间内连通性较好的节点多集中在信息技术行业,说明信息技术行业在深圳股票市场备受市场青睐。综合比较得出:在股市冲击降临时,上海股市连通性最好的金融行业和深圳股市连通性最好的信息技术行业更容易成为冲击的目标,所以监管部门要加强这两个行业的保护,以维护股市网络稳定。两个股市风险网络在不同极端行情下,网络连通性关键节点及其位置均发生显著变化,且上海和深圳股市网络连通性和关键节点均下降,从网络结构角度吻合了4.2节中从风险角度认为的2015年股市震荡破坏性强于2008年金融危机对我国股市的破坏性,从侧面反映出系统性风险的累积量越大在冲击发生时网络结构损坏越严重。
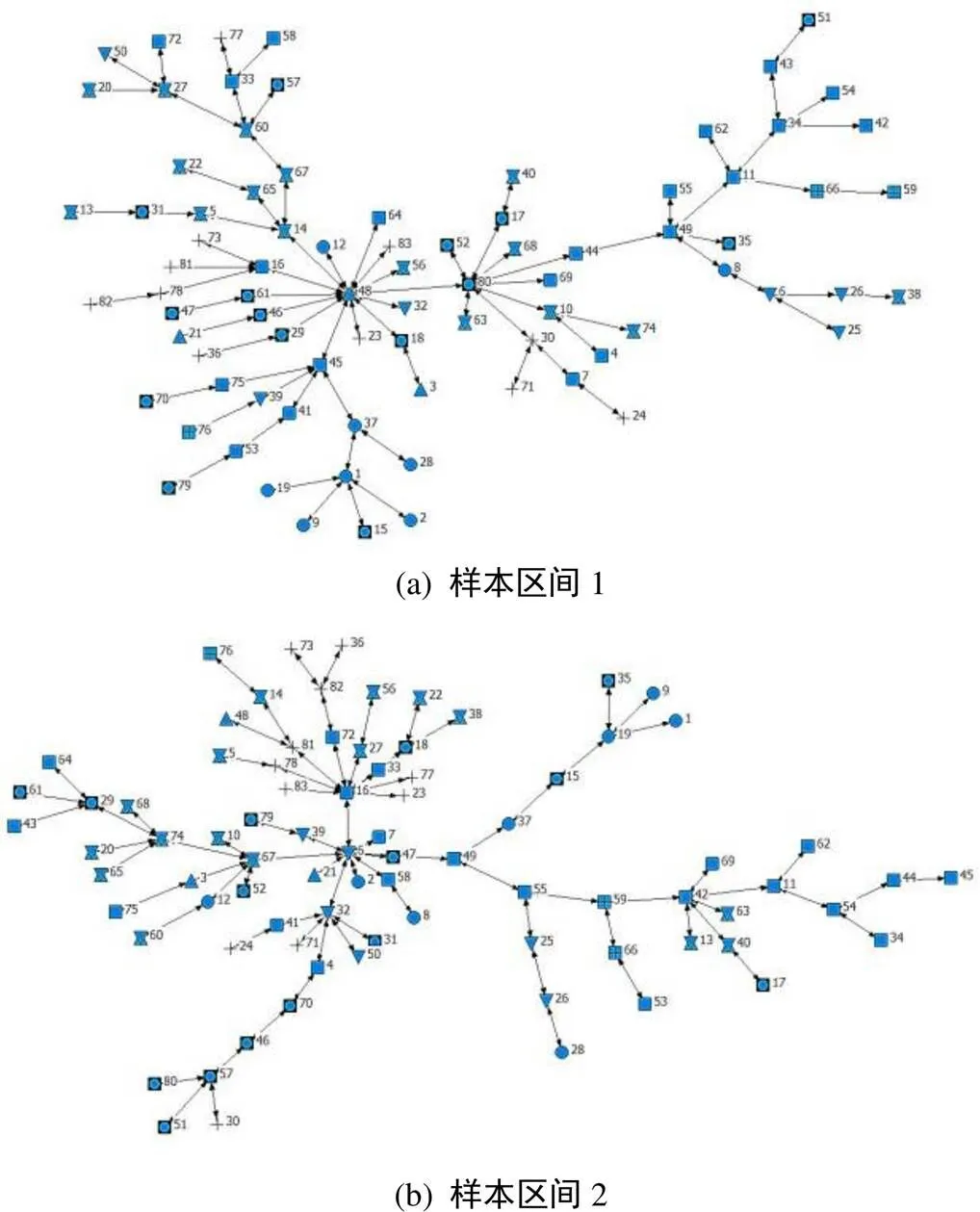
图5 深圳股票市场MST网络图(两样本区间)
Figure5 Shenzhen stock market MST network diagram in two samples
注:(1)形状代表的行业:圆形代表金融;正方形代表材料;上三角形代表工业;下三角形代表公用事业;盒形代表能源;圆在方形内代表可选消费,菱形代表电信服务,加号代表医疗保健;上下三角形代表信息技术;弧角方形代表日常消费。(2)编号:为了使图片更简洁,将公司股票代码按升序排列后从1到n依次编码。(3)箭头没有实际含义。
(2)度分布
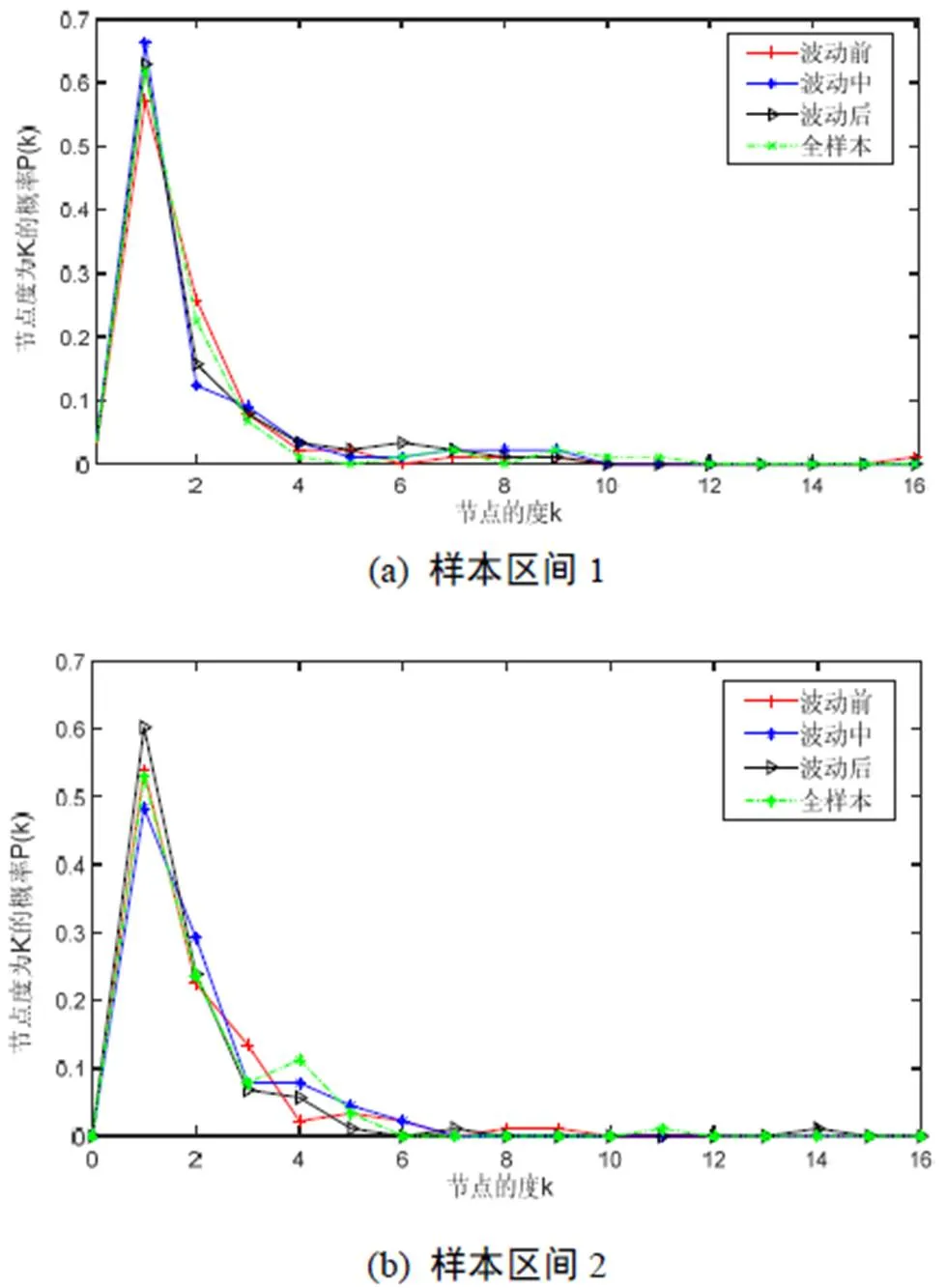
图6 上海股市网络图节点度分布(两样本区间)
Figure 6 Node distribution of Shanghai stock market network (two samples)
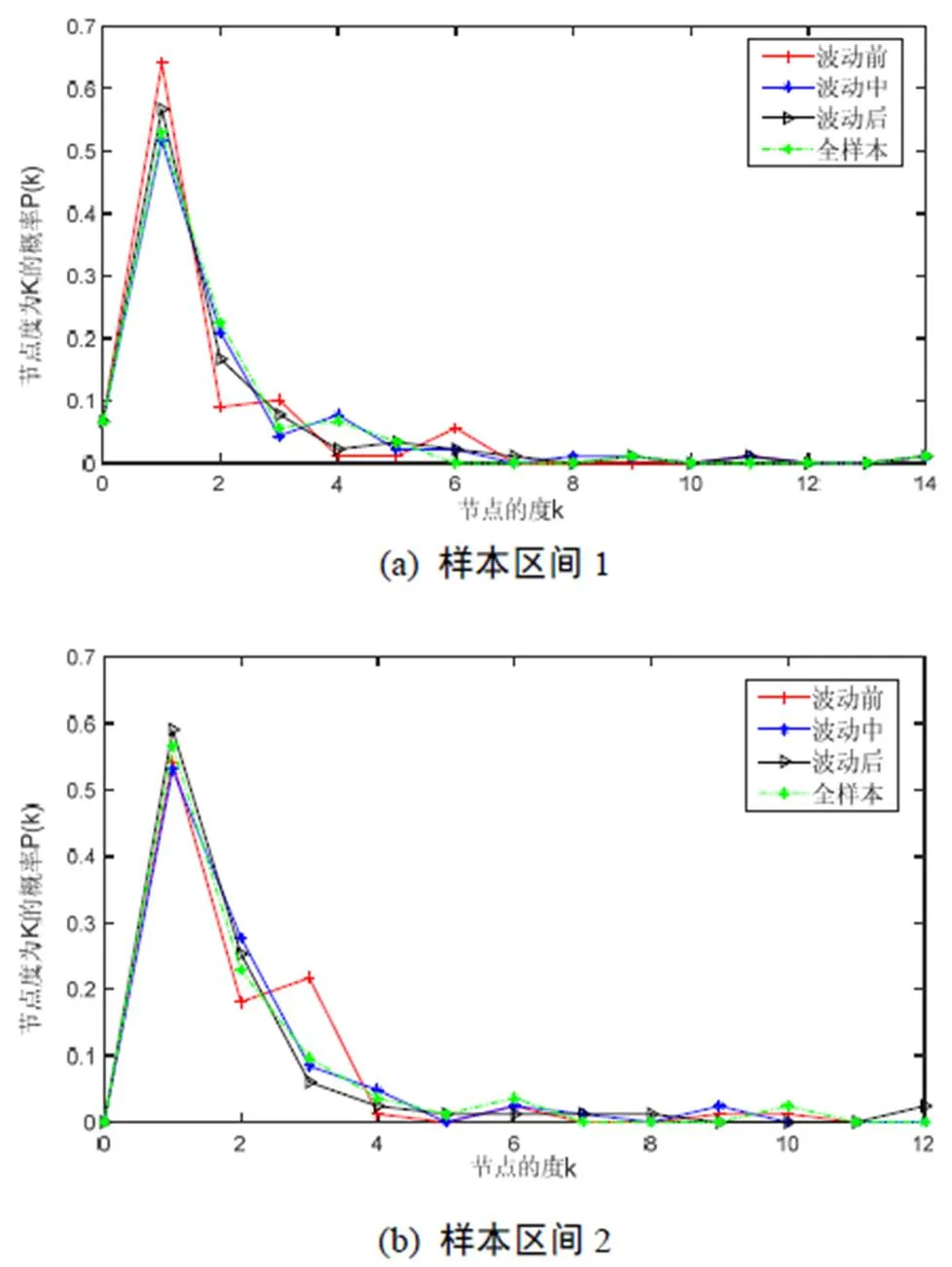
图7 深圳股市网络图节点度分布(两样本区间)
Figure 7 Node distribution of Shenzhen stock market network (two samples)
图6、图7看出沪深两市任意波动时期风险网络中大多数节点的度值小于平均度值2,且只有少数的节点度值大于5,这恰好是幂律分布的特征,即满足无标度网络的特点,说明上海和深圳股市风险网络为无标度网络。其次从图中看出在极端波动中两市场MST图的Hub节点均小于极端波动发生前、发生后,且在剧烈波动中度值为4~6的节点数显著高于波动前和波动后,说明沪深两市风险网络在危机波动的影响下起重要连通作用的高Hub节点数目减少致使网络结构发生改变,以抵抗风险波动与传染,维系股票市场稳定性。
(3)点强度和接近中心性

Figure 8 Node strength in Shanghai and Shenzhen stock markets in extreme fluctuation
图8、图9是在极端波动中上海和深圳股市风险网络每个节点的点强度和接近中心性,因篇幅限制极端波动发生前、后单只股票的点强度和接近中心性图并未给出。从上图看出,无论是上海还是深圳股市每个节点的点强度和接近中心性的值在两个极端波动区间都表现出明显的不同,尤其以上海股市在样本区间1的接近中心性值要显著大于样本区间2的接近中心性值,而就点强度来说沪深两市大多数节点的点强度都要小于1,有少数节点的点强度大于3。说明在不同传染源引起的极端波动行情下,股市网络结构调整差异明显,股市所受冲击越大(样本区间2)风险网络中节点的点强度和接近中心性值就越小。
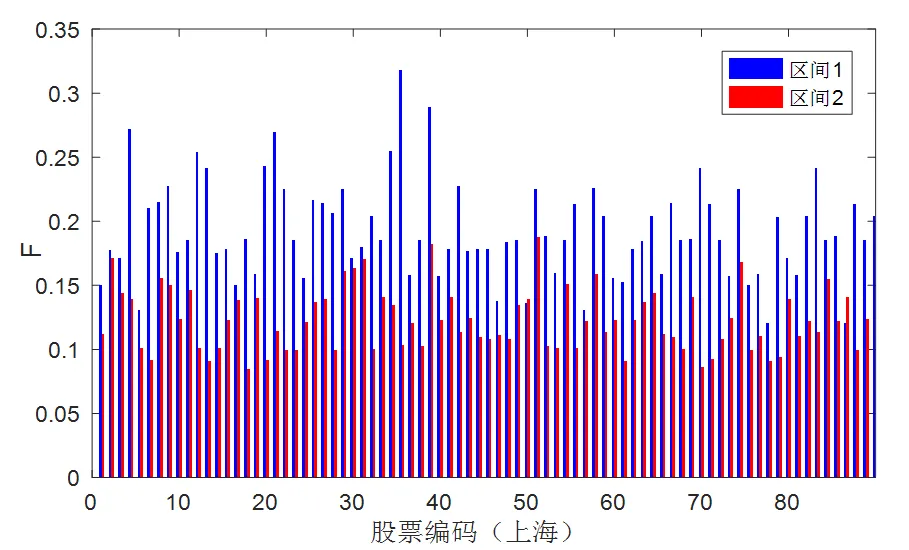
Figure 9 Node closeness centrality in Shanghai and Shenzhen stock markets in extreme fluctuation
4.5 dCoVaR与网络拓扑结构的回归分析
因本文研究样本是单个节点的行为特征,所以拒绝混合回归模型。再由Hausman检验结果中,故采用固定效应模型进行回归估计,得到上海和深圳股市在不同时间区间的动态面板回归结果如表1和表2所示。
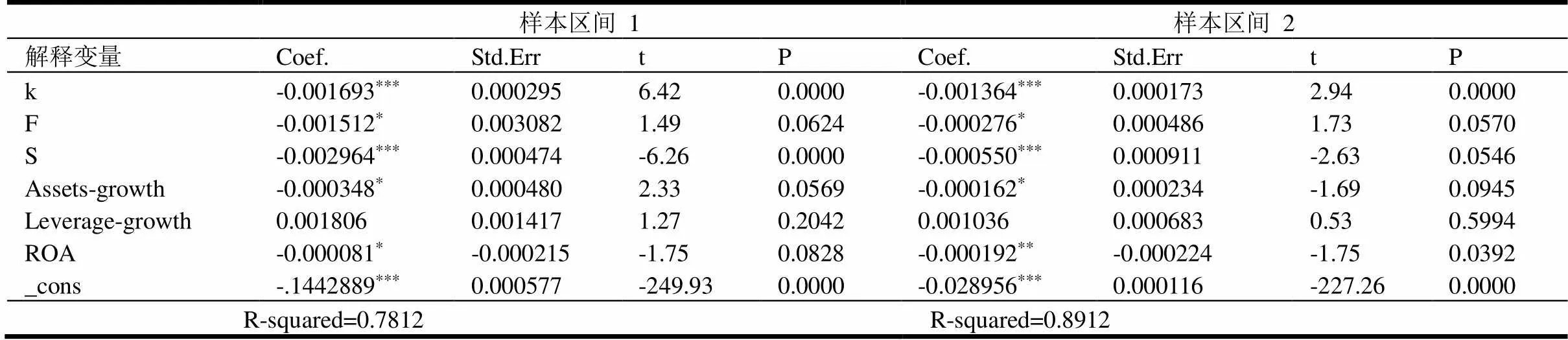
表1 上海股市动态面板回归结果
注:*、**、***分别表示在0.1、0.05和0.01的显著性水平下显著。

表2 深圳股市动态面板回归结果
注:*、**、***分别表示在0.1、0.05和0.01的显著性水平下显著。


4.5 稳健性检验
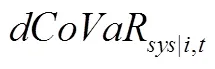

表3 中国股市动态面板回归结果
注:*、**、***分别表示在0.1、0.05和0.01的显著性水平下显著。

表4 不同时间跨度下中国股市动态面板回归结果
注:*、**、***分别表示在0.1、0.05和0.01的显著性水平下显著。
此外,我们同样考虑了其它可能影响到回归结果的影响因素,采取了多种稳健性检验:(1)考虑到采用VaR模型构建股市风险网络时,时间跨度的选取可能对股票的VaR造成影响,进而影响网络结构指标,所以另选取W=50,150构建沪深股市风险网络,表4给出回归结果。(2)考虑到不同分位数回归对因变量dCoVaR可能造成的影响,计算分位数=1%下的dCoVaR,回归结果如表5所示。观察表4和表5,结果显示:这些可能的影响因素都是计算中存在的误差,不同的时间跨度W和不同的分位数都不会对本文的结论产生实质性的影响,说明本文的结果具有较高的稳健性。

表5 不同分位数下中国股市动态面板回归分析结果(q=1%)
注:*、**、***分别表示在0.1、0.05和0.01的显著性水平下显著。
5 结论
本文创新性地利用风险价值VaR模型,通过股票间的风险相关性构建上海和深圳两个股票市场的风险价值网络,并探究在中国股市极端波动行情下(2008年国际金融危机和2015年国内股市剧烈震荡)风险价值网络的拓扑结构特征。将风险网络模型与动态面板回归模型相结合,利用分位数回归法计算股票网络中单只股票的条件在险价值CoVaR,进而确定股票网络中单只股票的系统性风险贡献度,分别从静态(总体)和动态(个体)视角分析上海和深圳股市系统性风险累积程度;最后利用动态面板回归分析网络结构指标与系统性风险贡献度间的关系,并通过样本外稳健性检验证明了相关关系的正确性。得出以下结论:
(1)上海股市系统性风险的累积程度要远大于深圳股市系统性风险的累积程度,即当在极端行情发生时上海股市比深圳股市更易爆发危机;两个极端行情下,样本区间2系统性风险累积程度大于样本区间1,同时风险网络重要节点拓扑指标在样本区间2也大幅降低,充分证明了2015年国内股市剧烈震荡对中国股市造成的冲击比2008年金融危机带来的冲击更严峻。提醒监管部门和投资者要格外警惕因我国自身股市因素造成的股市震荡。
(2)系统性风险的不断累积使风险溢出值达到局部最小的频率变大时,股市刚好处于危机爆发时期,而当单个股票的风险溢出值出现剧烈波动且振幅很大时,股票市场也恰好出现了极端波动,进而说明了股市的极端波动与风险的累积有相互作用关系。
(3)不同风险传染源引起的极端波动行情下,相同股票的系统性风险溢出值不同,即该股票对股市的风险贡献程度不同,故在投资选择上,要注意区别不同传染源引起的极端波动时相同股票持有量的变化。
(4)沪深两市的股票风险网络具有无标度特性,在上海股市风险网络中连接节点最多的集中在金融行业,说明金融业在上海股市受到极高的关注度;深圳股市风险网络中连通性较好的节点多集中在信息技术行业,说明信息技术行业在深圳股票市场备受青睐。暗示在极端冲击下这些行业更容易成为首选的冲击目标,对股市的系统性风险贡献度更大。
(5)在股票风险网络中,股票节点的节点度、接近中心性、点强度等网络拓扑指标与系统性风险溢出值呈显著的负相关关系,即这些拓扑指标值越大的节点,风险溢出值越小其对系统性风险贡献度就越大。最后的稳健性检验结果表明上述结果的可靠性。所以在股市极端波动发生时应加强对具有高节点度、高接近中心性和点强度的股票进行监管与防控,这些性质高的节点具有牵一发而动全身的网络作用。
[1] 欧阳红兵, 刘晓东. 中国金融机构的系统重要性及系统性风险传染机制分析——基于复杂网络的视角[J]. 中国管理科学, 2015, 23(10): 30-37.
Ouyang H.B, Liu X.D. An analysis of the systemic important and systemic risk contagion mechanism of China’s financial institutions based on network analysis[J]. Chinese Journal of Management Science, 2015, 23(10): 30-37.
[2] 唐振鹏, 谢智超, 冉梦,等. 网络视角下我国上市银行间市场系统性风险实证研究[J].中国管理科学, 2016, 24: 489-495.
Tang Z P, Xie Z C, Ran M, et al. Systemic risk empirical study of China listed bank market under the network perspective[J]. Chinese Journal of Management Science, 2016, 24: 489-495.
[3] Adrian T, Brunnermeier M K. Co-VaR Federal Reserve Bank of New York Staff Report, 2007, 348.
[4] Girardi G, Ergun A T. Systemic risk measurement: Multivariate GARCH estimation CoVaR [J]. Journal of Banking & Finance, 2013, 37(8): 3169-3180.
[5] 刘向丽, 顾舒婷. 房地产对金融体系风险溢出效应研究——基于AR-GARCH-CoVaR方法[J]. 系统工程理论与实践, 2014, 34: 105-111.
Liu X L, Gu S T. Research on risk spillovers from the real estate department to financial system based on AR-GARCH-CoVaR[J]. Systems Engineering—Theory & Practice, 2014, 34: 105-111.
[6] 高国华, 潘英丽. 基于资产负债表关联的银行系统性风险研究[J]. 管理工程学报, 2012, 26(4): 162-169.
Gao G H, Pan Y L. Research on banking systematic risk based on balance sheet association[J]. Journal of Industrial Engineering/ Engineering Management, 2012, 26(4): 162-169.
[7] Acharya V, Pedersen L, Philippon T, et al. Measuring systemic risk. mimeo, New York University, 2009.
[8] Krause A, Giansante S. Interbank lending and the spread of bank failures: A network model of systemic risk[J]. Journal of Economic Behavior and Organization, 2012, 83(3): 583-608.
[9] Iori G, Jafarey S, Padilla F G. System risk on the interbank market[J]. Journal of Economic Behavior & Organization, 2007, 61(4): 525-542.
[10] Marquez-Diez-Canedo J, Martinez-Jaramillo. Systemic Risk: Stress testing the banking system[C]. Amsterdam: International monetary fund & De nederlandsche bank, 2007.
[11] Mistrulli P E. Assessing financial contagion in the interbank market: Maximum entropy versus observed interbank lending patterns[J]. Journal of Banking & Finance, 2011, 35(5): 1114-1127.
[12] Gai S, Haldane A, Kapadia S. Complexity, concentration and contagion[J]. Journal of Monetary Economics, 2011, 58(5): 453-470.
[13] 李守伟, 何建敏. 不同网络结构下银行间传染风险研究[J]. 管理工程学报, 2007, 4(26): 71-78.
Li S W, He J M. Research on inter-bank contagion risk under different network structures[J]. Journal of Industrial Engineering/ Engineering Management, 2007, 4(26): 71-78.
[14] 贾彦东. 金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J]. 金融研究, 2011, 10: 17-33.
Jia Y D. Analysis of system importance of financial institutions- Systematic risk measurement and cost sharing in financial networks[J]. Journal of Financial Research, 2011, 10: 17-33.
[15] 陈国进, 马长峰. 金融危机传染的网络理论研究述评[J].经济学动态, 2010, 2:116- 119.
Chen G J, Ma C F. A researches review on network theories of financial crisis contagion[J]. Economic Perspectives, 2010, 2:116- 119.
[16] 范宏. 动态银行网络系统中系统中系统性风险定量计算方法研究[J]. 物理学报, 2014, 3: 465-471.
Fan H. Calculation of system risk in a dynamical bank network system[J]. Acta Phys. Sin., 2014, 3: 465-471.
[17] 巴曙松, 左伟, 朱元清. 金融网络及传染对金融稳定的影响[J]. 财经问题研究, 2013, 2: 3-11.
Ba S S, Zuo W, Zhu Y Q. The influence of financial networks and contagion on financial stability[J]. Research on financial and economic issues, 2013, 2: 3-11.
[18] 高波, 任若恩. 基于Granger因果网络模型的金融机构系统重要性评估[J]. 经济与金融, 2013, 6: 3-10.
Gao B, Ren R E. Measuring systemic importance of financial institutions based on Granger-Causality network model[J]. The economic and finance, 2013, 6: 3-10.
[19] 范小云, 方意, 王道平. 我国银行系统粉线的动态特征及系统性重要性银行的甄别——基于CCA与DAG相结合的分析[J]. 金融研究, 2013, 11: 82-95.
Fan X Y, Fang Y, Wang D P. Systemic risk and systemically important financial institutions of China’s bank section—an analysis based on CCA and DAG[J]. Journal of financial research, 2013, 11: 82-95.
[20] 隋聪, 迟国泰, 王宗尧. 网络结构与银行系统性风险[J]. 管理科学学报, 2014, 4: 57- 70.
Sui C, Chi G T, Wang Z Y. Network structure and systemic risk by banks[J]. Journal of Management Sciences in China, 2014, 4: 57- 70.
[21] 邓超, 陈学军. 基于多主体建模分析的银行间网络系统性风险研究[J]. 中国管理科学, 2016, 1(24): 67-75.
Deng C, Chen X J. Studyon multi-agent models analyses for systemic risk from the interbank network[J]. Chinese Journal of Management Science, 2016, 1(24): 67-75.
[22] 王占浩, 郭菊娥, 薛勇. 资产负债表关联、价格关联与银行间风险传染[J]. 管理工程学报, 2016, 2(30): 202-210.
Wang Z H, Guo E J, Xue Y. International financial contagion based on direct relations of balance sheets and assets price[J]. Journal of Industrial Engineering/Engineering Management, 2016, 2(30): 202-210.
[23] Huang W Q, Zhuang X T, Yao S, et al. A financial network perspective of institution’s systemic risk contributions[J]. Physica A, 2016, 456: 183-196.
[24] Nikos P, Dimitrios G, Renatas K, et al. Transmission channels of systemic risk and contagion in the European financial networks[J]. Journal of Banking & Finance, 2015, 61: 336-352.
[25] 隋聪, 谭照林, 王宗尧. 基于网络视角的银行业系统性风险度量方法[J]. 中国管理科学, 2016, 24(5): 54-64.
Sui C, Tan Z L, Wang Z Y. A network perspective measurement method for banking systemic risk[J]. Chinese Journal of Management Science, 2016, 24(5): 54-64.
[26] 邓向荣, 曹红. 系统性风险、网络传染与金融机构系统重要性评估[J]. 中央财经大学学报, 2016, 3: 52-60.
Deng X R, Cao H. systemic risk, network contagion and assessment of SIFIs[J]. Journal of Central University of Finance & Economics, 2016, 24(5): 54-64.
[27] 谢家泉. 股灾背景下中美股票风险溢出的结构转换研究[J]. 运筹与管理, 2017, 2 (26): 127-135.
Xie J Q. Structural transfer research about risk spillover between Chinese stock market and American stock market based on stock market disaster[J]. Operations research and management science, 2017, 2 (26): 127-135.
[28] 庄新田,张鼎,苑莹,等. 中国股市复杂网络中的分形特征[J]. 系统工程理论与实践, 2015, 35(2): 273-282.
Zhuang X T, Zhang D, Yuan Y, et al. Fractal characteristic of the Chinese stock market complex network[J]. Systems Engineering—Theory & Practice, 2015, 35(2): 273-282.
[29] Adrian T, Brunnermeier M K. CoVaR [R]. National Bureau of Economic Research, 2008.
[30] Adrian T, Brunnermeier M K. CoVaR [J]. American Economic Review, 2016, 106 (7): 1705-1741.
[31] Jorion P. Value at risk [M]. 3rd ed. McGraw-Hill, 2006.
[32] 孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2015.
Sun X J, Si S K. Algorithms and Applications of Complex Networks[M]. Beijing: National Defense Industry Press, 2015.
[33] Hendricks, D. Evaluation value-at-risk using history data[J]. Economy Policy Review, 1996, 2: 39-70.
[34] Kruskal, J B. On the shortest spanning subtree of a graph and the traveling salesman problem[J]. Proc. Amer. Math. Soc, 1956, 7(1): 48–50.
[35] 李云红, 魏宇, 吴晓雄. 中国股票市场适应性特征的实证研究[J]. 管理工程学报, 2016, 1(30): 72-80.
Li Y H, Wei Y, Wu X X. Empirical study of the adaptability features on Chinese stock markets[J]. Journal of Industrial Engineering/ Engineering Management, 2016, 1(30): 72-80.
Stock market network topology and systematic risk contribution:Based on VaR network model
ZHANG Weiping, ZHUANG Xintian*, LI Yanshuang
(School of Management, Northeastern University, Shenyang 110169, China)
The stock market is a high-risk market, and its systematic risk is a result of continuous cumulative changes manifesting into extreme fluctuations. Large fluctuations in stock prices, such as the 2008 and 2015 stock disasters, are due to sudden stock price crashes at particular points in a short period of time. These crashes have caused huge losses to investors, and reflect that the stock price volatility coefficient cannot accurately characterize the long-term equilibrium relationship between stock prices. Therefore, in this paper we build a stock market risk network model based on the value-at-risk (VaR) model, and use CoVaR to measure the overflow value (conditional VaR) of the risk of a single stock price in the stock market system. Because the VaR model provides an effective way to measure market risk, and the correlation coefficient of the VaR array reflects the correlation between the risks of stocks, this provides a new perspective for studying the systematic risk, risk transmission, and network stability of stock markets.
First, we use the quantile regression method to calculate the conditional value-at-risk CoVaR of a single stock in the stock risk network, then determine the systematic risk contribution of a single stock in the stock network, and finally, analyze the cumulative degree of systematic risk in Shanghai and Shenzhen stock markets from a static (general) and dynamic (individual) perspective. The results show that the cumulative degree of systematic risk in the Shanghai stock market is much greater than that in the Shenzhen stock market. That is, when extreme market conditions occur, the Shanghai stock market is more prone to crisis than the Shenzhen stock market. The impact of Chinese stock markets’ extreme fluctuations in 2015 was more severe than that of the 2008 financial crisis.
Second, based on the VaR model, the value-at-risk network of the Shanghai and Shenzhen stock markets is constructed to reflect the correlation between the risks of their stocks, and the topological structure characteristics of the value-at-risk network under the extremely volatile conditions of Chinese stock markets are explored. It is found that the stock market risk networks of both locations have scale-free characteristics; high-connectivity in the Shanghai stock market risk network is concentrated in the financial industry, and high-connectivity in the Shenzhen stock market risk network is concentrated in the information technology industry, indicating that these industries are more likely to become the preferred targets for shocks when their respective stock markets are impacted by fluctuations, such that their impact will contribute more to the risk of the system.
Finally, the dynamic panel regression model is used to analyze the relationship between the network structure index and the degree of systematic risk contribution, and the correctness of the correlation is proved by a robustness test. In the stock risk network, network topology indicators such as the node degree, closeness of centrality, and node strength of the stock markets are significantly negatively correlated with the systematic risk overflow value - that is, the greater the value of the network topology indicator of the node, the smaller the overflow value of its risk, and the greater the contribution of that risk to overall systematic risk.
VaR (Value at Risk) model; Risk network; Network topology; Systemic risk contribution; Stock market extreme fluctuations
2018-04-10
2018-07-10
Supported by the Natural Science Foundation of China (71671030,71571038)
F830.91
A
1004-6062(2020)04-0171-011
10.13587/j.cnki.jieem.2020.04.019
2018-04-10
2018-07-10
国家自然科学基金资助项目(71671030、71571038)
庄新田(1956—),男,吉林四平人;东北大学工商管理学院教授,博士生导师;研究方向:金融复杂网络,供应链金融,金融工程。
中文编辑:杜 健;英文编辑:Boping Yan
