2017年全国主要城市废水排放情况统计分析及其对策

蔡正群，江畅，刘家保

(1.安徽建筑大学 外国语学院，安徽 合肥 230601；2.安徽建筑大学 数理学院，安徽 合肥 230601)

0 引言

我国近几年来工业迅速发展，经济稳步增长的同时也拉动着人民消费水平的提升，过度的消耗使得水资源形势严峻[1]。同时，我国庞大的人口基数使得资源更加稀缺，而这种情况下，水资源受到的破坏程度丝毫没有降低。工业生产排放和生活污水排放是废水排放的两大来源[2]。目前，保护水环境质量，满足不同功能需求是世界上许多国家面临的一个共同难题，解决这个难题就要从分析问题的源头出发[3-5]。

1 数据来源

实验数据如表1 源自国家统计局官方网站《中国统计年鉴2018》。在这里将污染物的来源主要归为6 类，分别标记为，X1：工业废水排放量，X2：工业化学需氧量排放量，X3：工业氨氮排放量，X4：城镇生活污水排放量，X5：生活化学需氧量排放量，X6：生活氨氮排放量。

2 主要城市废水排放情况统计分析

2.1 2017年主要城市废水排放情况的描述性分析

本文对主要城市废水中污染物的排放情况进行描述统计分析，主要概念和符号参考文献[6-10]。

由表2 可以看出，在城市废水的主要污染物排放中，城镇生活污水排放量的情况最为严重，最小值为3 477 万t，最大值达到181 252 万t，平均值为59 499.3226 万t；工业氨氮排放量最少，最小值为13 t，最大值为1 969 t，平值为355.0323 t。排放量由多到少依次为：城镇生活污水排放量、生活化学需氧量排放量、生活氨氮排放量、工业废水排放量、工业化学需氧量排放量、工业氨氮排放量。综上所述，2017 年我们所分析的主要城市废水中主要污染物来源于城镇生活废水的排放。

2.2 废水排放量与地区生产总值之间的相关分析

2.2.1 相关分析的目的

相关分析是一种分析事物之间客观关系的统计方法，要想理解并应用相关分析，了解客观事物之间的关系至关重要。客观事物之间的关系可大致分为函数关系和统计关系，函数关系即两者或多者之间存在着可以用明确的式子表达出的关系，而统计关系却没有这么直接，虽然确实存在，但难以一目了然，并且这种关系有的强，有的弱，相关分析正是测度两者或多者之间统计关系的简单有效的工具[10-12]。

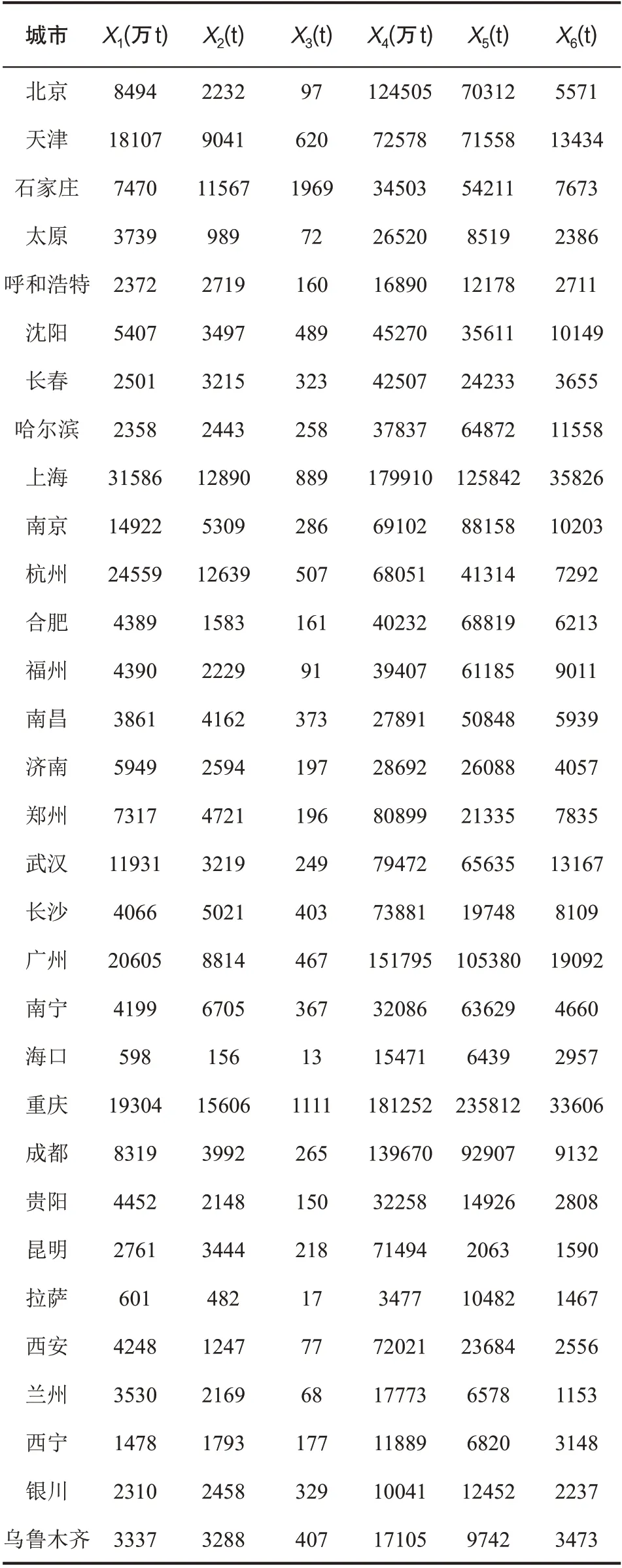
表1 主要城市的废水排放情况(2017年)

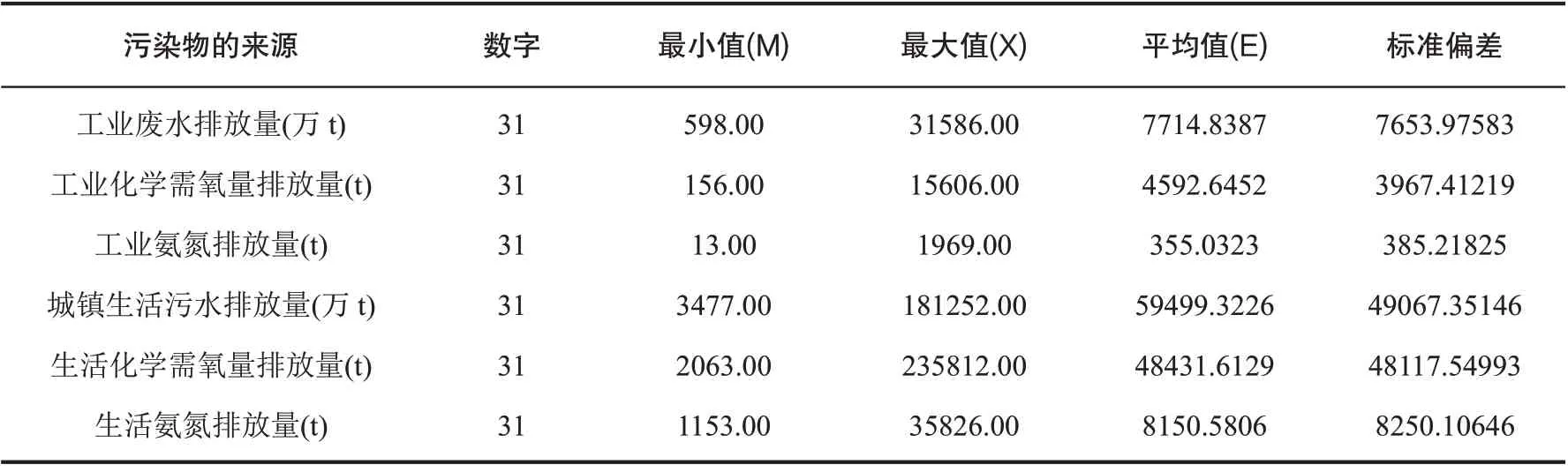
表2 主要城市废水中污染物排放情况描述统计量

2.2.2 相关系数

由于统计关系强弱程度并不相同，为了有效地衡量事物之间关系的强弱，提出了相关系数的概念，记作r。相关系数r 的取值在-1～+1 之间，其大小与事物之间关系强弱的对应情况如表3 所示。

表3 相关系数与变量之间关系的对应情况

2.2.3 Pearson 简单相关系数

用Pearson 简单相关系数[13]来度量废水中6 种主要污染物变量与地区生产总值X7变量间的线性相关关系，其思想可以用数学公式表达为：

本文对主要城市废水中主要污染物的排放与地区的生产总值做相关分析。地区生产总值数据来源于《中国统计年鉴2018》，将其标记为X7，见表4。

表5 给出了6 种主要污染物与地区生产总值之间的Pearson 相关系数，从中可以看出，地区生产总值X7与X1、X2、X3、X4、X5、X6的相关系数分别为0.521，0.338，0.144，0.429，0.330，0.295。在置信度(双侧)为0.01 的情况下，地区生产总值与工业废水排放量呈高度正相关性，在置信度(双侧)为0.05时，相关性是显著的，即地区生产总值与城镇生活污水排放量呈高度正相关性。

表4 地区生产总值(2017年)

2.3 2017年主要城市废水排放情况的聚类分析

2.3.1 聚类分析的目的

聚类分析是将事物进行分类的统计方法，它根据数据的某些特征对要观察的数据或变量进行分类。如果没有事先了解，数据或变量将根据性质上的亲和度自动分类，以产生多个类别结果。通过“物以类聚”，来更好地发现数据或变量间的规律[13-15]。

表5 Pearson相关系数

2.3.2 变量个体间距离的计算方式

本文区间的度量标准选择欧氏距离(Euclidean Distance)计算。其数学定义为：

表6 2017年主要城市中各地区的分类情况

由表6 可知，当聚成4 类时，北京、广州、成都为一类，天津、石家庄、太原、呼和浩特、沈阳、长春、哈尔滨、南京、杭州、合肥、福州、南昌、济南、郑州、武汉、长沙、南宁、海口、贵阳、昆明、拉萨、西安、兰州、西宁、银川、乌鲁木齐为一类，上海及重庆各成一类。当聚成3 类时，北京、上海、广州、成都为一类、重庆自成一类，剩下的主要城市为一类。当聚成2 类时，重庆自成一类，剩下的主要城市为一类。通过这些分类结果，可初步得到各地区的分类情况。

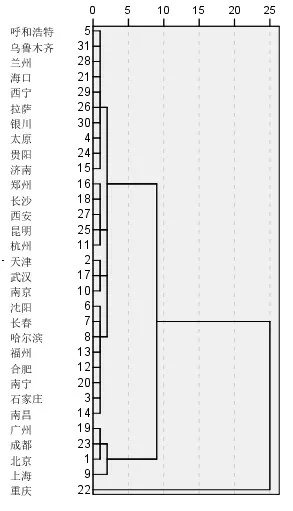
图1 层次聚类分析的树状图

根据图1 聚类分析结果，可以将31 个主要城市分为如下三类：

第一类：北京，广州，成都，上海。

第二类：天津，呼和浩特，沈阳，长春，哈尔滨，南京，杭州，合肥，石家庄，太原，福州，南昌，济南，郑州，武汉，长沙，南宁，海口，贵阳，昆明，拉萨，西安，兰州，西宁，银川，乌鲁木齐。

第三类：重庆。

2.4 2017年主要城市废水排放中主要污染物的因子分析

2.4.1 因子分析的数学模型和相关概念

因子分析是一种在信息损失最小的条件下，从多个因素中提取几个因素的统计方法。数学定义式如下所示：

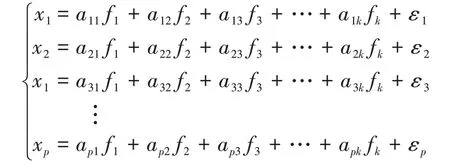
2.4.2 判断前提条件

因子分析的目的就是得到具有代表性的因子从而解释原有变量，这里使用相关系数矩阵、KMO和巴特利特球度检验方法，来检验主要城市废水排放中的6 种主要污染物是否适合进行因子分析。

表7 是废水排放中6 个主要变量的相关系数矩阵。可以看出，大部分的相关系数都较高，各变量之间呈较强的线性关系，可以从中提取公共因子，适合进行因子分析。

由表8 可知，巴特利特球度检验统计量的观测值为177.671，相应的概率P-值接近0。如果显著性水平α 为0.05，由于P-值小于显著性水平α，则应拒绝原假设，认为相关系数矩阵与单位阵有显著差异。同时，KMO 值为0.743，根据Kaiser 给出的KMO 度量标准可知原有变量适合进行因子分析。

本文对全国31 个主要城市废水排放中的6 种主要污染物进行因子分析，得到各地区的废水排放总体情况。

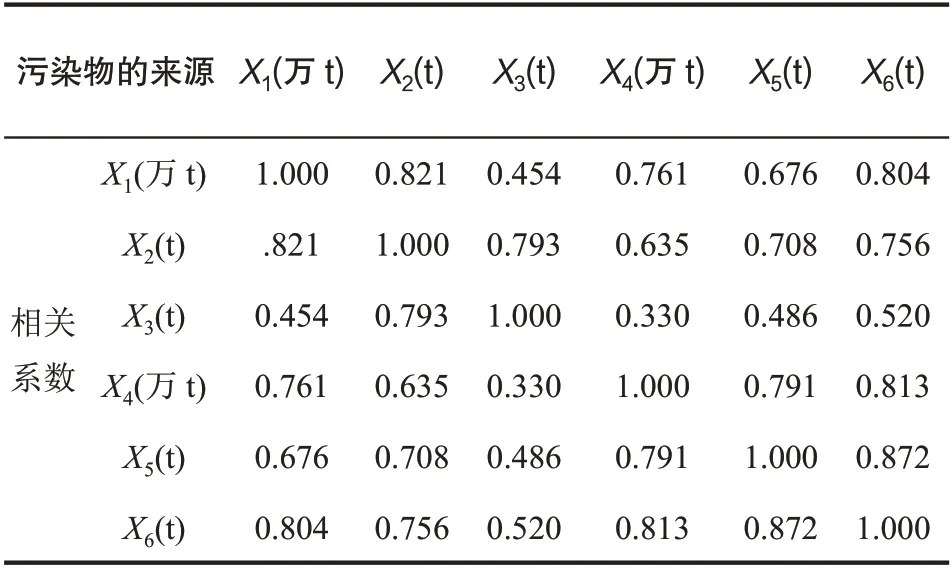
表7 原有变量的相关系数矩阵

表8 巴特利特球度检验和KMO检验

由表9 的总方差解释可以看出，这两个因子解释了原始变量总方差的88.176%，原有信息丢失较少，因子分析效果理想。

从图2 碎石图中可以看出，第1 个因子的特征值最大，对解释原有变量的贡献最大，第2 个介于两者之间，第3 个和后续因子的特征值较小，对原始变量的贡献较小，可以舍弃，因此选择提取2 个因子是合适的。

根据表10 可以写出6 种主要污染物的因子分析模型：

工业废水排放量X1= 0.885f1- 0.118f2，

工业化学需氧量排放量X2= 0.910f1+ 0.321f2，

工业氨氮排放量X3= 0.673f1+ 0.709f2，

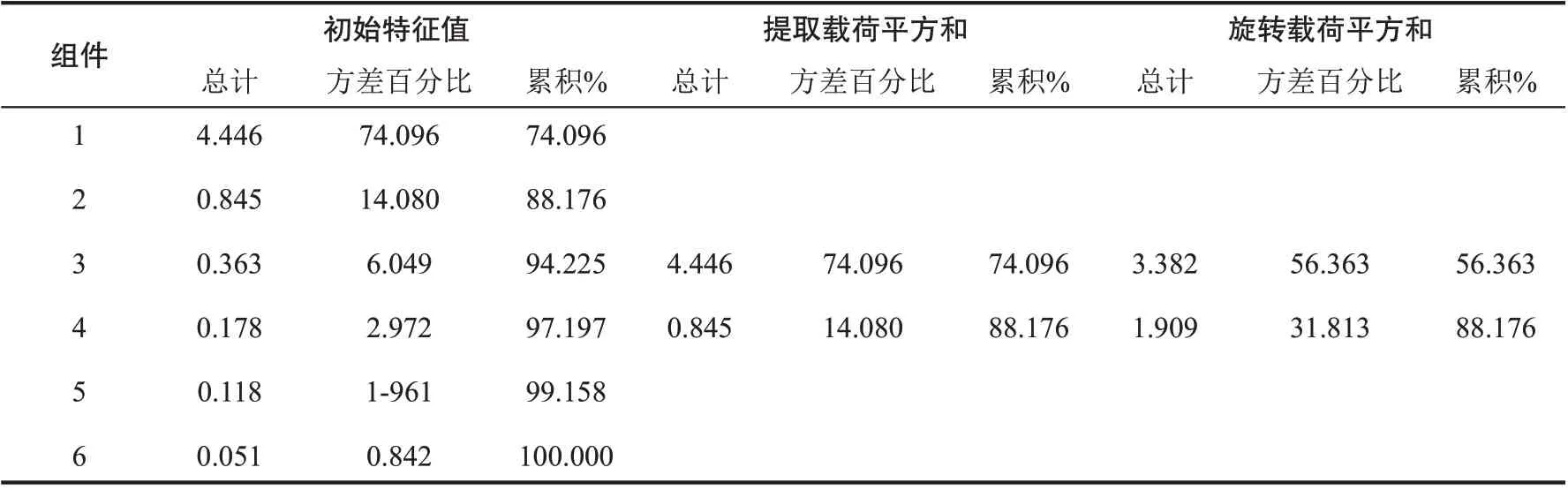
表9 因子解释原有变量总方差的情况

城镇生活污水排放量X4= 0.851f1- 0.401f2，

生活化学需氧量排放量X5= 0.887f1- 0.189f2，

生活氨氮排放量X6= 0.933f1- 0.168f2。

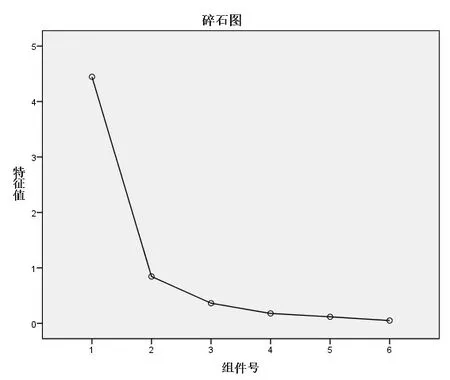
图2 因子分析的碎石图

表10 因子载荷矩阵

表11 旋转后的因子载荷矩阵

由表11 可知，城镇生活污水排放量、生活氨氮排放量、生活化学需氧量排放量在第1 个因子上有较高的载荷，第1 个因子主要解释了这几个变量，可解释为生活废水排放量；工业废水排放量、工业氨氮排放量、工业化学需氧量排放量在第2 个因子上有较高的载荷，第2 个因子主要解释了这两个变量，可解释为工业化学废水排放量。

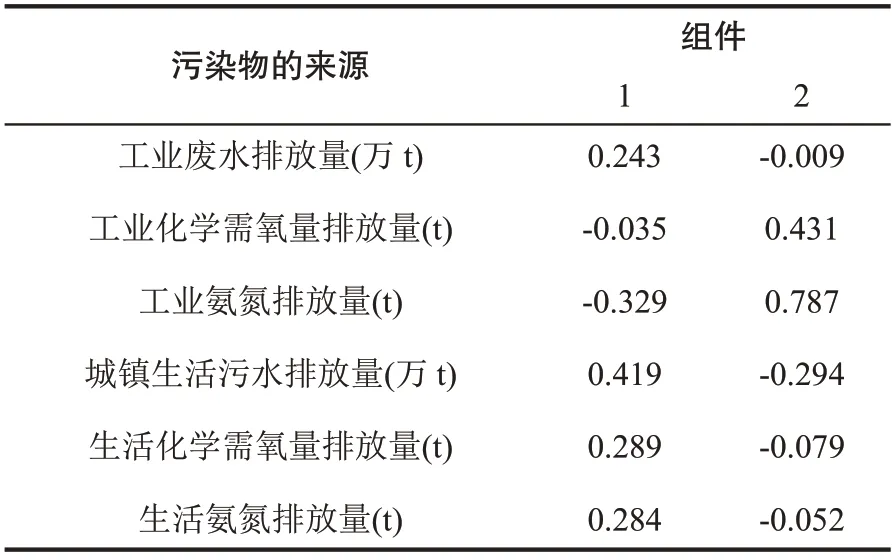
表12 废水排放成分得分系数矩阵

根据表12 可以写出因子得分函数：

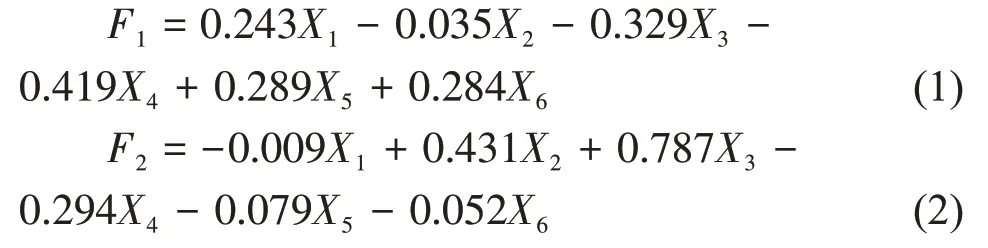
由函数(1)、(2)可知，工业氨氮排放量和城镇生活污水排放量的权重较高，这两者的数值高低更能反映该地区的废水排放情况。

2.4.3 主要城市废水排放情况的综合评价

根据因子得分变量对31 个地区绘制散点图进行综合研究。这里绘制了两因子得分的散点图。

图3 我国主要城市两因子得分的散点图

由图3 可见，北京、上海是较为特殊的点，其他地区相似。北京和上海的两个成分得分都很高，表明这两个地区工业上和城镇生活中的废水排放量都很大，这与它们发达的城市工业、快速的消费发展是相关的，部分城市第1 因子得分高，第2 因子得分较低，像天津、武汉、南京等，表明由工业发展造成的污水排放量比城镇生活造成的更为严重。

其次，对全国31 个主要城市废水中污染物的排放量进行综合评价，运用计算加权总分的方法，由函数(1)、(2)可以计算出各地区的得分及排名。将权重确定为各公共因子对方差的贡献率占总方差贡献率的比重，得分及排名情况如表13 所示。

由表13 可以看到，2017 年全国主要城市废水排放情况的各公因子得分有正有负，得分为正表示污染物排放量高于全国平均水平，得分为负则表示污染物排放量低于全国平均水平。通过上述分析，可以得出结论：重庆、上海、广州、成都、北京这样的经济发达城市与其他主要城市无论是在生活废水排放上还是工业废水排放上都存在差异，废水排放量较大。

表13 我国主要城市在各公因子上的得分及排名表

3 结果分析

将废水中的污染物提出主要6 种，分别标记为：工业废水排放量X1、工业化学需氧量排放量X2、工业氨氮排放量X3、城镇生活污水排放量X4、生活化学需氧量排放量X5、生活氨氮排放量X6。这6 种中，城镇生活废水的排放量最大，高达181 252 万t。且地区的经济发展状况与废水排放情况是相关的，在置信度为0.01 的情况下，地区生产总值与工业废水排放量呈高度正相关性，在置信度为0.05 的情况下，地区生产总值与城镇生活污水排放量呈高度正相关性，所以在经济发展的同时必须注重保护生态环境，关注绿色发展。

由聚类分析，将全国31 个主要城市分成了几类，发现重庆是个特殊地区，自成一类；北京，广州，成都，上海为一类；天津，呼和浩特，沈阳，长春，哈尔滨，南京，杭州，合肥，石家庄，太原，福州，南昌，济南，郑州，武汉，长沙，南宁，海口，贵阳，昆明，拉萨，西安，兰州，西宁，银川，乌鲁木齐为一类。

在因子分析的综合得分计算后，得到重庆在第一个公因子和综合得分上均排第一名，说明重庆的生活污水排放量较大。通过因子分析建立的模型，可以看出主要城市的废水排放情况，其中生活废水排放占比较大，包括城镇生活污水排放量、生活化学需氧量、生活氨氮排放量，其次是工业化学废水排放量，包括工业化学需氧量排放量、工业氨氮排放量、工业废水排放量。并通过绘制散点图及计算加权总分的方法，对全国31 个主要城市进行综合研究，得出结论：重庆、上海、广州、成都、北京这样城市生活丰富、经济发展迅速的地区，与其他主要城市无论是在生活废水排放上还是工业化学废水排放上都存在差异，废水排放量较大。

4 对策措施

加强对全国水资源污染问题的治理，必须对这些城市目前存在的问题加以重视，政府及相关部门可以从以下几方面加强注意。

(1) 加强废水排放的管理

我国废水排放有一套严格的法律体系，这其中每一项指标都有具体数字可循，这些排放标准是根据受纳水体的水质要求，再结合环境特点和社会、经济、技术条件等诸多因素综合考虑做出的，要求各地工厂、污水治理厂等强制执行。广度达到的同时对深度也有要求，制度的普及是一方面，更要看能够达标的有多少，不能够达标的又是因为什么原因，相关职能部门对制定的污水治理方案要有雷厉风行的魄力，这也反过来要求所制定的方案是符合当地实情的，是切实可行的。

(2) 加强废水处理工艺

目前国内废水处理主要还是延续从前的工艺，脱硫废水在废水池中由废水提升泵送入中和、沉淀、絮凝箱处理，后经澄清池溢流至出水箱，在箱中经过pH 调整后达标排放。这样做基本能够达到排放标准，但废水中有一部分物质含量较高，是不允许直接排放的，排放工艺可以在这一环节进行改善和加强，提高污水处理的效率。提高政府对于工业废水剔除氨氮的要求，加大此类科研创新经费和关注度，从源头上保证废水排放的安全性，促进生态可持续发展。

(3)加强公众保护水资源意识

由于污水排放与经济利益挂钩，而且地区生产总值与城镇生活污水排放量呈高度正相关性，越是经济发达的地区，废水排放量更大，导致部分人从中偷工减料，这是水资源保护意识缺乏的表现。总体上，我国是一个干旱缺水严重的国家，水资源总量并不丰富，人均占有量更低，废水排放若得不到改善只会加重对淡水资源的污染，因此要大力宣传，增强意识等。