基于实测过载的弹体侵彻姿态角计算模型
2020-09-07张铱翔牛少华陶逢刚孙远程刘天国
张铱翔,牛少华,唐 彬,陶逢刚,孙远程,刘天国
(1.北京理工大学 机电学院, 北京 100081;2.中国工程物理研究院 电子工程研究所, 四川 绵阳 621999)
对高价值硬目标的精确打击和高效毁伤,在现代战争中起着越来越重要的作用。为了实现对目标的最佳毁伤效果,要求侵彻弹引信能够实时有效地对侵彻过程进行识别和判断,并采取相应的策略对弹药进行控制和起爆[1-2]。弹体在侵彻过程中,由于受到目标的作用,其姿态会发生变化。弹体侵彻姿态变化一方面会影响对侵彻信息的识别,另一方面则会对其侵彻能力产生影响。目前,关于对弹体侵彻机理及炸药控制方面的研究较多[3-6],而在弹体侵彻姿态识别方面的研究相对较少。弹体飞行姿态的识别,在弹体导引系统和引信系统中通常可采用由陀螺和加速度传感器构成惯性测量单元来实现,李慧[7]采用磁强计、加速度计和陀螺复合系统进行测量,曹红松等[8]利用地磁矢量和陀螺探测结果解算弹体姿态,杜烨等[9]采用二轴磁强计和MEMS陀螺对弹箭进行测量,但是对于高速侵彻弹药,在侵彻目标过程中,弹体及内部结构将经历极其恶劣的高冲击过载环境的作用,而目前已有的陀螺无法适应这种环境,因此研究基于加速度传感器获取的侵彻过载计算得到弹体的侵彻姿态具有十分重要的工程意义。张建新等[10]研究了基于两个三轴加速度传感器轨迹计算方法,但存在一定的不足之处,该方法中将传感器测得的加速度默认为是靶板坐标系下的加速度。但实际上,由于加速度传感器是安装于弹体引信内,其实测得到的加速度实际上是弹体自身运动坐标系下的加速度,因此,研究基于加速度传感器实时测得的过载计算得到弹体侵彻姿态很有必要,也具有更好的工程实用价值。
1 弹体运动坐标与靶板固定坐标
在弹体侵彻靶板过程中,靶板相对地面是固定的,弹体相对地面是运动的,为研究弹体相对靶板的侵彻姿态,建立如图1所示的坐标系,其中OXYZ是以靶板为参考系的固定坐标系,O′X′Y′Z′、O″X″Y″Z″、O‴X‴Y‴Z‴是基于弹体自身建立的运动坐标系,弹体沿v0方向撞击靶板。t0时刻弹体运动坐标系O′X′Y′Z′与靶板固定坐标系OXYZ方向一致,撞击靶板后,弹体姿态可能会发生改变。根据弹体姿态变化可分为A、B两种情况。对于A情况,弹体姿态变化较小,弹体运动坐标系O″X″Y″Z″与O′X′Y′Z′的角度变化也较小,弹体在OXYZ坐标系中Z向承受的过载较大,在坐标系O′X′Y′Z′中Z′向承受的过载较大,X′、Y′向承受的过载较小;对于B情况,弹体姿态变化很大,弹体运动坐标系O‴X‴Y‴Z‴与O′X′Y′Z′的角度变化很大,弹体在OXYZ坐标系中Z向承受的过载较大,在坐标系O′X′Y′Z′中Y‴向承受的过载较大,X‴、Z‴向承受的过载较小。由于加速度传感器是固定于弹体内,其测得的是沿弹体轴向和径向过载,若将传感器测得的加速度等同于固定坐标系下的加速度来计算弹体姿态,则会产生较大的误差,因此研究基于加速度传感器实时测得的加速度计算得到弹体侵彻姿态很有必要。

图1 弹体运动坐标系与靶板固定坐标系
2 弹体实时侵彻姿态
弹体侵彻过程中,三维加速度传感器测得的轴向加速度az(t),径向加速度ax(t),ay(t),加速度方向分别与运动坐标系的坐标轴一致。

式中:vz(t)为t时刻运动坐标系下的弹体轴向速度,vx(t)、vy(t)为t时刻运动坐标系下的弹体径向速度,z(t)为t时刻运动坐标系下的弹体轴向位移,x(t)、y(t)为t时刻运动坐标系下的弹体径向位移。
在弹体实际的侵彻过程中,需要对三轴加速度传感器的过载信号进行实时处理,此时二次积分从0时刻到t时刻的过载信息将无法保证计算的时效性。
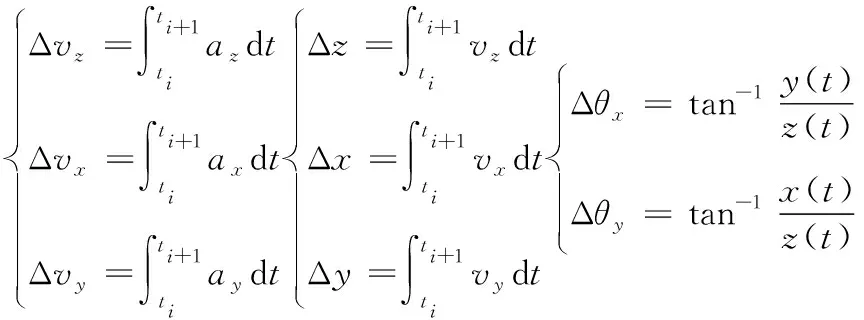
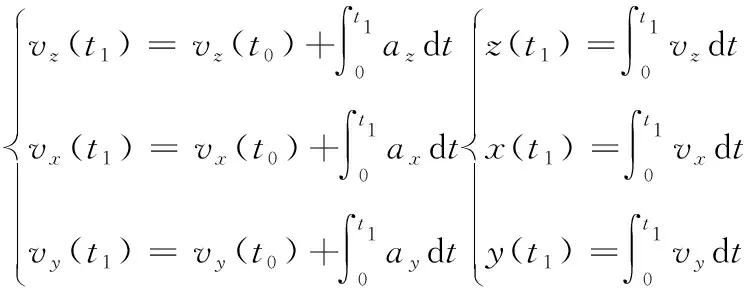

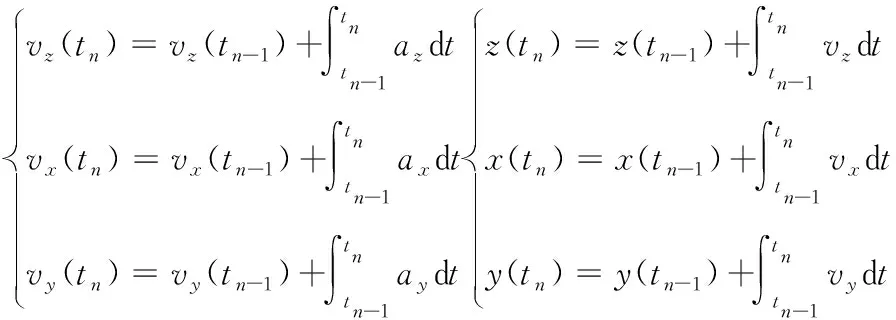
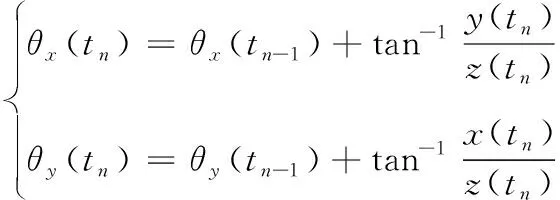
在实时计算过程中,每一时刻进行一次速度、位移、角度变化以及姿态角的计算,将前一时刻的结果与变化量进行叠加得到新的结果。
3 数值仿真及结果分析
在弹体实际侵彻过程中,加速度传感器无法得到弹体的姿态角变化曲线,因此选用数值仿真方法对一工况进行仿真,将仿真所得过载信息通过坐标系变换得到传感器实测过载信息,并进行姿态角计算,将计算结果与仿真结果进行对比。
采用有限元动力学软件LS-DYNA对弹体斜侵彻多层加筋钢靶板进行数值仿真,弹体采用各向同性弹塑性模型(*MAT_PLASTIC_KINEMATIC),靶体采用Johnson-Cook材料模型(*MAT_JOHNOSN_COOK)以及Gruneisen状态方程(*EOS_GRUNEISEN),弹体和靶板分别为G50钢和922A(10CrNi2MoCu)钢,材料参数分别见表1、表2。弹体为φ400 mm×1 300 mm的截卵型弹体,头部长560 mm,卵型半径为1 000 mm,靶板为含T型加强筋的均质靶板,弹体初始速度为1 200 m/s,计算时间步长为10 μs。通过数值仿真可以得到三轴加速度传感器在靶板固定坐标系下的轴向加速度以及径向加速度,如图2所示。

表1 弹体材料参数

表2 靶体材料参数
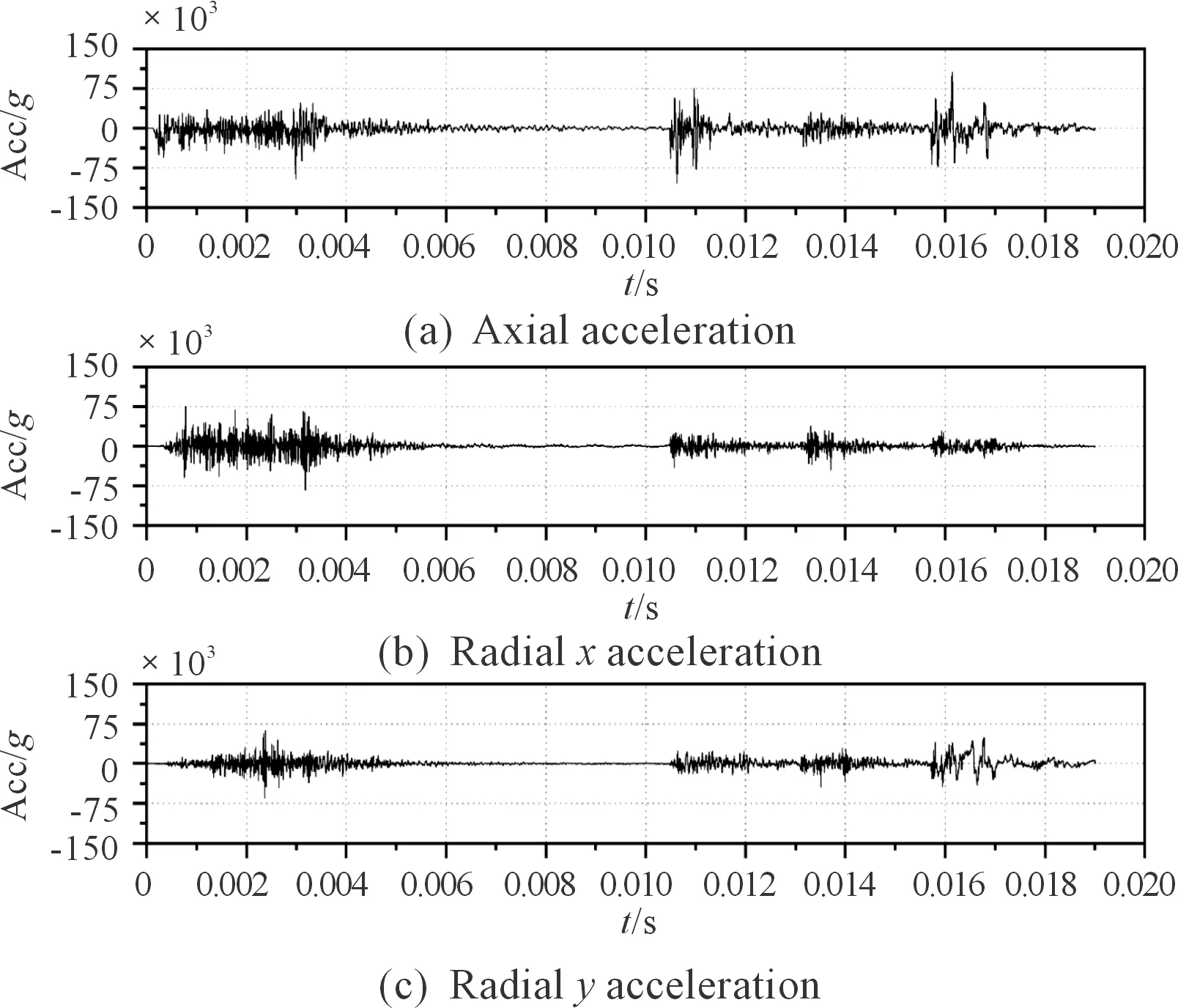
图2 仿真过载得到的轴向加速度及径向加速度曲线
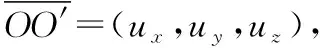

图3 空间坐标系与运动坐标系变换示意图
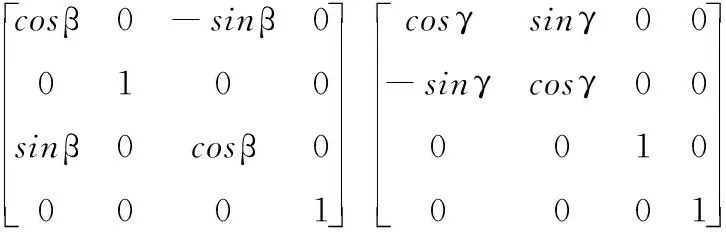
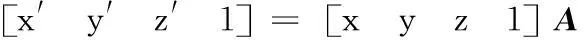
式中:矩阵A为空间固定坐标系到弹体运动坐标系的变换矩阵。将仿真数据代入坐标系变换公式得到新的实测过载,如图4所示。
图5为仿真所得姿态角与实测计算所得姿态角的对比,两者变化趋势基本相同,但计算结果在某些时刻不能很好描述姿态角的细微变化,这是由于二次积分所产生的误差所导致,最大误差在5°左右。结果表明通过三轴加速度传感器实测过载计算弹体偏转角在理论上是可行的,仿真结果对比验证了计算模型的有效性。
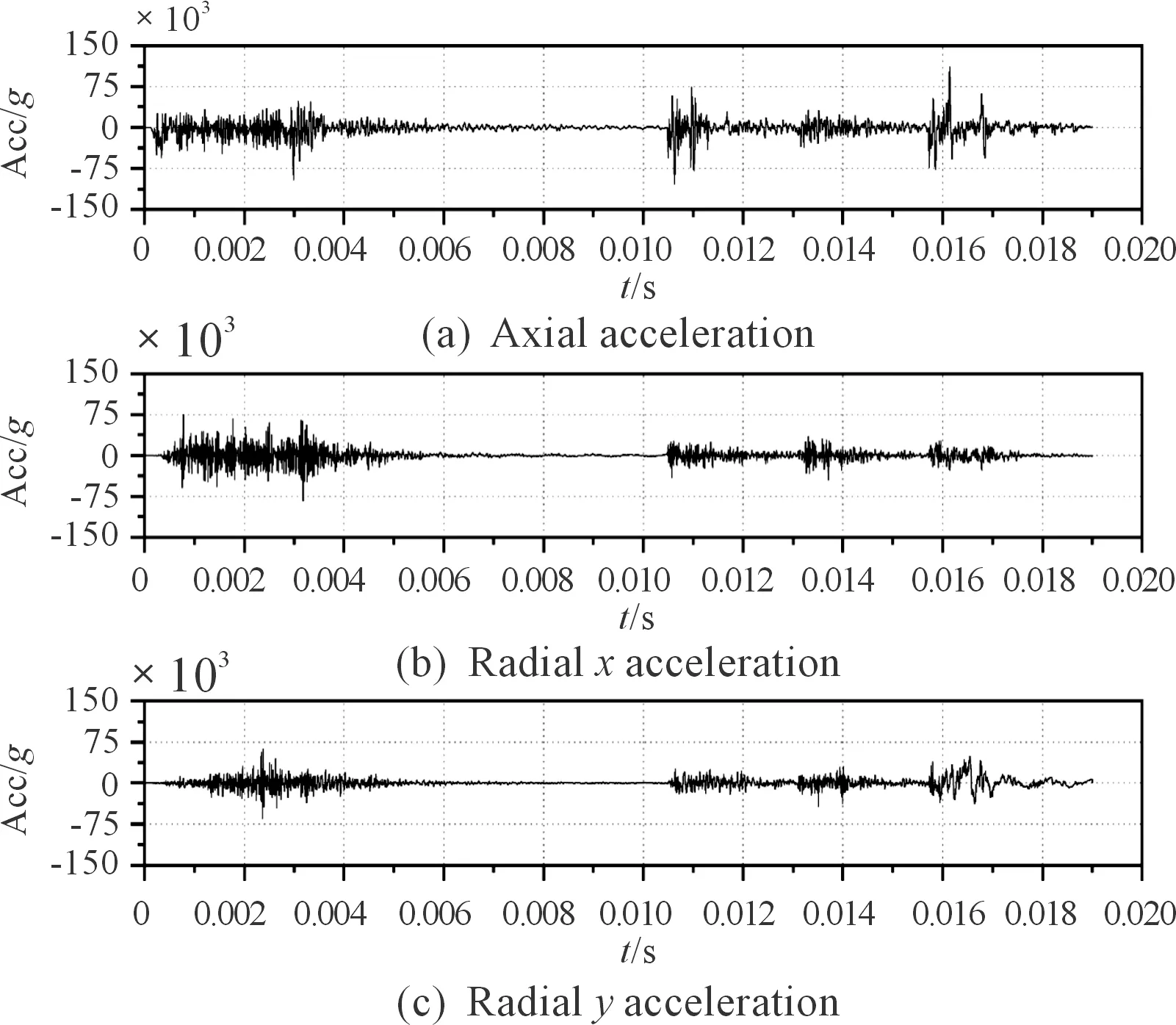
图4 计算过载得到的轴向速度及径向速度曲线
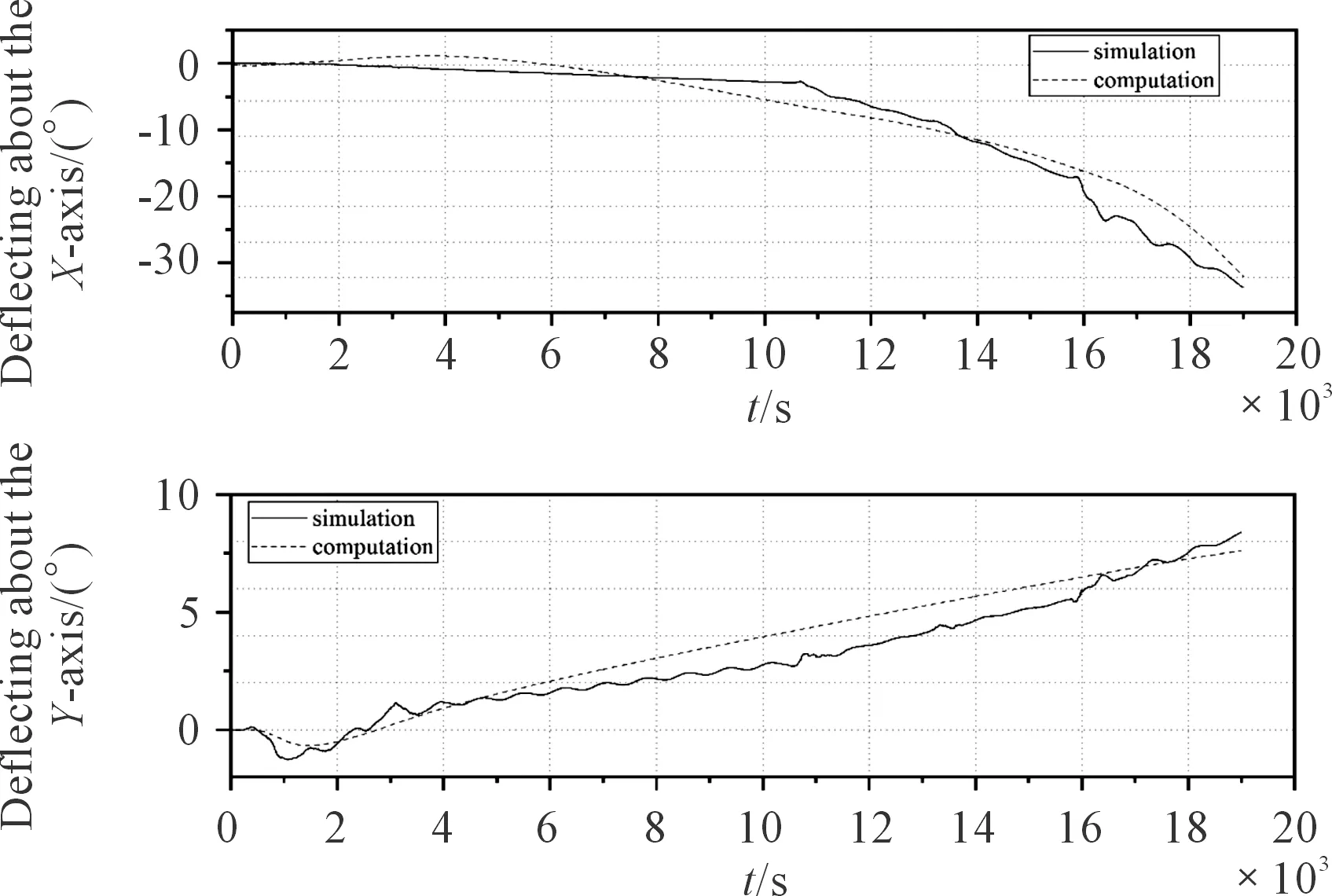
图5 仿真与实测姿态角曲线
4 结论
针对弹体连续侵彻多层靶板,在弹体初始着速、着角已知的情况下,从坐标系变化出发,在弹体姿态角变化较大的情况下,通过三轴加速度传感器推导出了弹体姿态角的计算模型;采用LS-DYNA有限元分析软件进行了仿真分析,并将仿真获得的三轴加速度信号进行坐标系变换,通过MATLAB程序计算,对该算法进行了验证。作者提供了一种基于三维加速度传感器的弹体姿态角变化实时计算方法,对侵彻引信识别具有参考价值。
