基于分层符号有向图的二回路系统故障诊断

2020-09-07张龙飞胡鹏飞

兵器装备工程学报 2020年8期

马杰，张龙飞，彭俏，胡鹏飞

(1.海军工程大学核科学技术学院，武汉 430033; 2.海军装备部，西安 710001)

核动力装置二回路系统设备复杂，运行工况复杂多变，操纵员如果不能及时判断并处置运行过程中发生的故障，可能会造成严重的后果。利用智能的故障诊断技术对核动力装置二回路系统进行诊断，不仅可以有效判断运行故障，而且可以防止重大事故的发生[1]。现阶段常用的智能故障诊断模型有定性[2]、定量和半定量[3]三种，定性模型采用基于深层知识的方法，具备识别未知故障及自动获取知识的特点，基于分层符号有向图(Signed Directed Graph，SDG)故障诊断也是一种基于深层知识的智能诊断方法，广泛应用于航天[4]、化工、煤矿等行业复杂系统的故障诊断。

现阶段利用SDG模型的进行故障诊断，主要利用各个变量节点间的关系，通过有效的推理机制和推理算法，得到故障演变传播的路径，进而找到真正的故障源，具有良好的完备性和鲁棒性[5]。但利用传统SDG模型推理故障源时，系统越复杂越容易出现“组合爆炸”问题，产生多义性，使得诊断效率不高[6]。

本研究针对核动力装置二回路系统，以SDG故障诊断模型为基础，根据传统SDG方法对潜在故障源搜索范围大、诊断效率低等问题，建立分层符号有向图(SDG)模型。通过分层策略减小潜在故障源搜索空间，再利用分层SDG模型进行推理获得故障源及故障相容通路，最后通过二回路系统仿真实验对分层SDG故障诊断模型进行验证。

1 分层SDG模型原理

1.1 SDG模型

SDG模型可以利用不同符号和连线来描述系统内部影响关系的定性因果模型，通过关键参数之间的因果关系，推理出故障可能的传播路径，具有包容大量潜在故障信息的能力。对SDG模型定义如下：

G=(V，E，φ，θ)

(1)

其中节点集合V代表系统可能故障根源，支路集合E表示节点间的因果关系，φ代表正、负影响，θ表示节点状态集合。

V={v1,v2,…,vn}表示节点集合；

E={e1,e2,…,en}表示支路集合；

邻接关系符δ+∶E→V(支路的起始节点)和δ-∶E→V。(支路的终止节点)，该“邻接关系”分别表示每一个支路的起始节点δ+ek和终止节点δ-ek；

函数φ：E∈{+,-}称为支路ek的符号；

函数θ：V∈{+,0,-}其中θ(vj)(vj∈V)为节点vj的符号；

以上定义是假定系统的状态描述为状态变量相应于每个元素的值，这些值可以取为正常状态值，也可以大于或小于正常状态值。

SDG模型G=(V，E，φ，θ)的故障模式是一个函数：

(2)

1.2 SDG推理机制

SDG模型的推理是在模型中完备地且不重复地搜索(穷举)所有的相容通路的过程，称为SDG的定性仿真，通过对相容通路的搜索，就可以发掘出故障在复杂系统内部的发展演变过程，找到故障源。实时高效的推理是SDG模型定性仿真的基础和关键。

SDG模型一般有反向推理和正向推理两种推理机制，反向推理就是在模型的瞬态报警样本中，从当前报警节点向反向搜索所有可能的原因节点，遍历可能的报警相容通路，并确定潜在故障源。正向推理从潜在故障源开始，正向搜索所有相容通路，若发现与监测参数状态不一致的故障源为虚假故障源，反之则认为该故障源为可能故障源。

1.3 分层SDG模型

分层SDG模型是传统SDG模型的一种改进，是通过可达性矩阵行集合、列集合之间的矩阵运算，将有向图分层后再进行故障诊断。分层结构代表了故障源的层次，任何本层内的节点故障只能影响到本层或下层的节点状态，而不能影响到上一层的节点状态。分层SDG表示了系统内故障报警传播层次结构，当节点参数状态异常出现警报后，根据报警节点所在层次，先从位于最高层的报警节点开始诊断，能够缩小搜索空间，提高诊断效率。

定义SDG模型的先行集为Ai，可达集为Ri，所有能够到达节点组成Ai，所有vi到达的节点组成Ri。分层SDG模型Gk的数学模型表示如下：

Gk=(Vk,Ek,ω)

(3)

式中：集合Vk={vh|vh为第h层所有节点}，h为节点的层数；

函数ω：ω(eh,h+1)(eh,h+1∈EF,ω→{+,-})，各支路节点间的符号集合；集合Ek={eh|eh为第h层和h+1层节点间的所有有向边}采用基于可达性的分层方法，具体算法为：

步骤1：对每个节点寻找可达集Ri和先行集Ai；

步骤2：首先计算可达集Ri和先行集Ai的交集，对交集与Ai相同的节点vi的集合，就是第1层节点定义L1，第1层节点的集合为：

L1={vi|Ri∩Ai=Ai}

(4)

步骤3：删除所有已经确定层次的节点，再删除与这些节点相连的有向边，就会产生一个新的SDG模型。对新的SDG模型所有节点重复1和2，分别计算第2到h层的节点集合，直到所有节点进行分层，第h层节点集可以表示为：

Lh={vi|vi∈V-L1-L2-,…-Lk-1,Ri∩Ai=Ai}

(5)

图1为一个SDG模型，其中包含7个节点变量，其中箭头表示了这些节点间的相互影响关系。

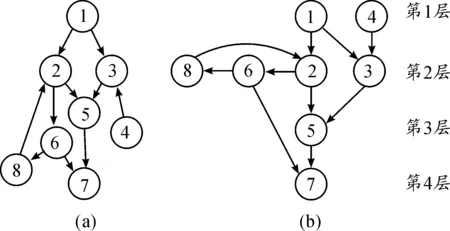
图1 分层SDG模型示意图

通过分析有向图节点关系，可以确定图1(a)未分层的SDG模型的可达矩阵：

设节点1的可达集为R1，由P1可得R1={2,3,5,6,7,8}，设节点1的先行集为A1，由P1可得A1={φ}。则有：R1∩A1=R1∩φ=φ=A1，根据式(4)可知节点1为第1层节点。用同样的方法继续搜索其他所有节点，得到节点4也是第1层的节点，则第1层节点集合为：

L1={节点1,节点4}

确定第1层节点后，删除节点1和节点4所在的行和列后，重新建立可达矩阵，新的可达矩阵为：

对于可达矩阵P2，应用同样的推理方法，确定第2层节点为：

L2={节点2,节点3,节点6,节点8}

以此类推完成SDG模型的分层，如图1(a)为原始的SDG模型，图1(b)为经过分层后的SDG模型。

如果SDG模型建立的邻接矩阵通过上述算法不能直接进行分层，需要在邻接矩阵基础上通过Warshall算法先转化为可达矩阵在进行分层，邻接矩阵A可通过Warshall算法公式(6)转化为可达矩阵P：

P=A+A2+A3+…+An

(6)

2 核动力二回路系统分层SDG模型

在核动力装置故障诊断领域，由于装置系统的复杂性，对故障诊断的实时性和完备性要求很高。故障发生后如果不能及时判断可能短时间内出现大量继发报警，这就要求建立的诊断算法复杂程度不能过高。因此，本研究将分层有向图策略应用于核动力装置二回路系统故障诊断建模，利用分层SDG方法减少搜索空间，提高故障源的诊断效率。

2.1 二回路系统分层SDG模型

核动力装置二回路系统包括主蒸汽系统、辅蒸汽系统、凝给水系统等子系统，主要循环过程是蒸汽发生器产生的高温高压的蒸汽，进入汽轮机做功后，经冷凝器凝结成水，在经过预热后通过凝水泵和给水泵重新进入蒸发器，完成整个汽水循环过程[7]。根据二回路系统流程建立核动力装置二回路系统的SDG模型(其结构参见图2)。

图2 核动力装置二回路系统SDG模型结构示意图

由于核动力装置二回路系统比较复杂，变量之间的关系相互耦合，需要选取关键参数对SDG模型进行简化，要求关键参数(见表1)能够快速、准确地识别故障，并能解释核动力装置二回路系统发生故障的参数变化过程。

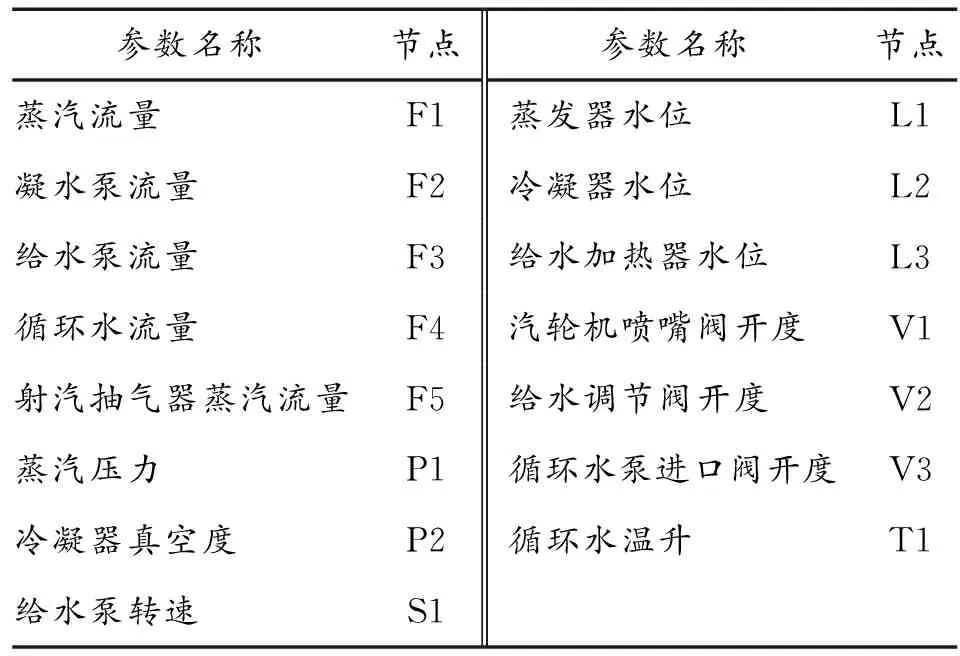
表1 二回路系统关键参数

分析关键参数与故障之间的影响关系，根据二回路系统流程分析各参数间的影响关系，结合简化后的SDG模型建立邻接矩阵和可达矩阵。应用SDG模型分层方法，建立核动力装置二回路系统分层SDG模型如图3所示。

2.2 分层SDG模型推理机制

在核动力装置二回路系统SDG模型基础上，根据工艺流程及分层策略建立了分层SDG故障诊断模型。根据系统实时采集的运行数据输入到分层SDG模型，判断节点变量的状态，由分层SDG进行推理，判断故障并得到故障传播路径。节点状态的判定，需要确定每个被测变量的阈值，通常使用的刚性阈值范围较难把握，范围较小，灵敏度过高，报警容易出现组合爆炸，范围较大，可能遗漏报警导致故障诊断无法进行[8]。这里引入节点阈值模糊判定方法，即5级SDG模型的模糊隶属度。

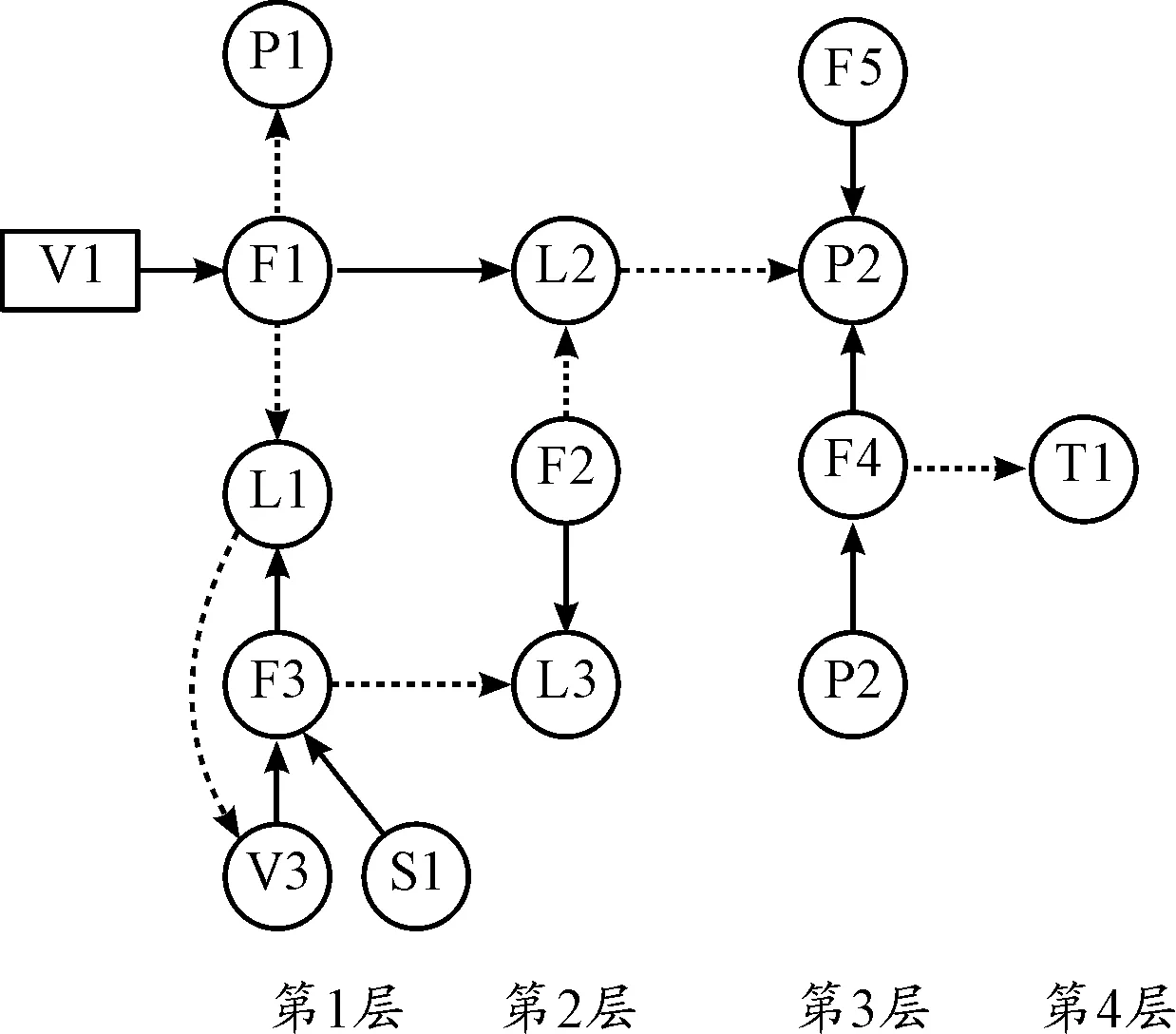
图3 二回路系统分层SDG模型结构示意图

设定5级SDG节点阈值为a*、a、b、b*，其中(a，b)为节点参数的正常范围，节点状态为“0”。a*和b*分别为上下限报警阈值，在a*、b*范围以外节点状态为“+”或“-”，在区间(a*，a)和(b，b*)为灰色区间，表示节点参数超出了正常范围，但还没有超过报警阈值，将此范围内的偏差映射到线性隶属函数上，表示该节点参数存在偏差的程度，即节点状态“+”或“-”的程度。

基于分层SDG模型故障搜索采用反向推理算法，算法流程如图4所示。首先，系统发生故障后，被监控节点处的系统变量异常，发出报警，建立报警节点。从报警节点集合中，选取最底层的一个报警节点，开始搜索，采用反向搜索方式，在分层SDG模型中，反向搜索各个支路，如果支路为不相容支路，则该不相容支路对应的设备为潜在故障源。如果相容，则该设备没有发生故障，只是起到了传播故障的作用，那么继续反向搜索，最后报警集合的所有报警节点都被反向搜索后，所获得的潜在故障源组成故障源侯选集。将故障源侯选集中每个潜在故障源分别进行正向推理验证，如果与报警监测值一致的话，判断该故障报警为故障源，并给出故障传播路径。

3 基于分层SDG故障诊断模型的仿真实验

本文研究以核动力模拟机作为运行数据源，对核动力装置二回路系统凝水泵故障、冷凝器真空度低故障进行仿真实验研究。

3.1 凝水泵故障

核动力装置凝水泵故障是指二回路系统运行过程中，凝水泵因机械或电气原因导致停止运行。在凝水泵发生故障后，如果处置不当，可能导致冷凝器真空下降，蒸发器干锅等严重后果，因此，需要及时判明故障。

仿真实验初始条件是模拟机设置为30%功率运行，在正常运行50 s后，在模拟机上调用故障设置模式，停止凝水泵运行。根据模拟机异常工况下的瞬时样本数据(见表2)，对瞬时样本数据按照线性模糊隶属度算法转换后，得到各监测节点的模糊隶属度。

图4 分层SDG模型推理流程框图

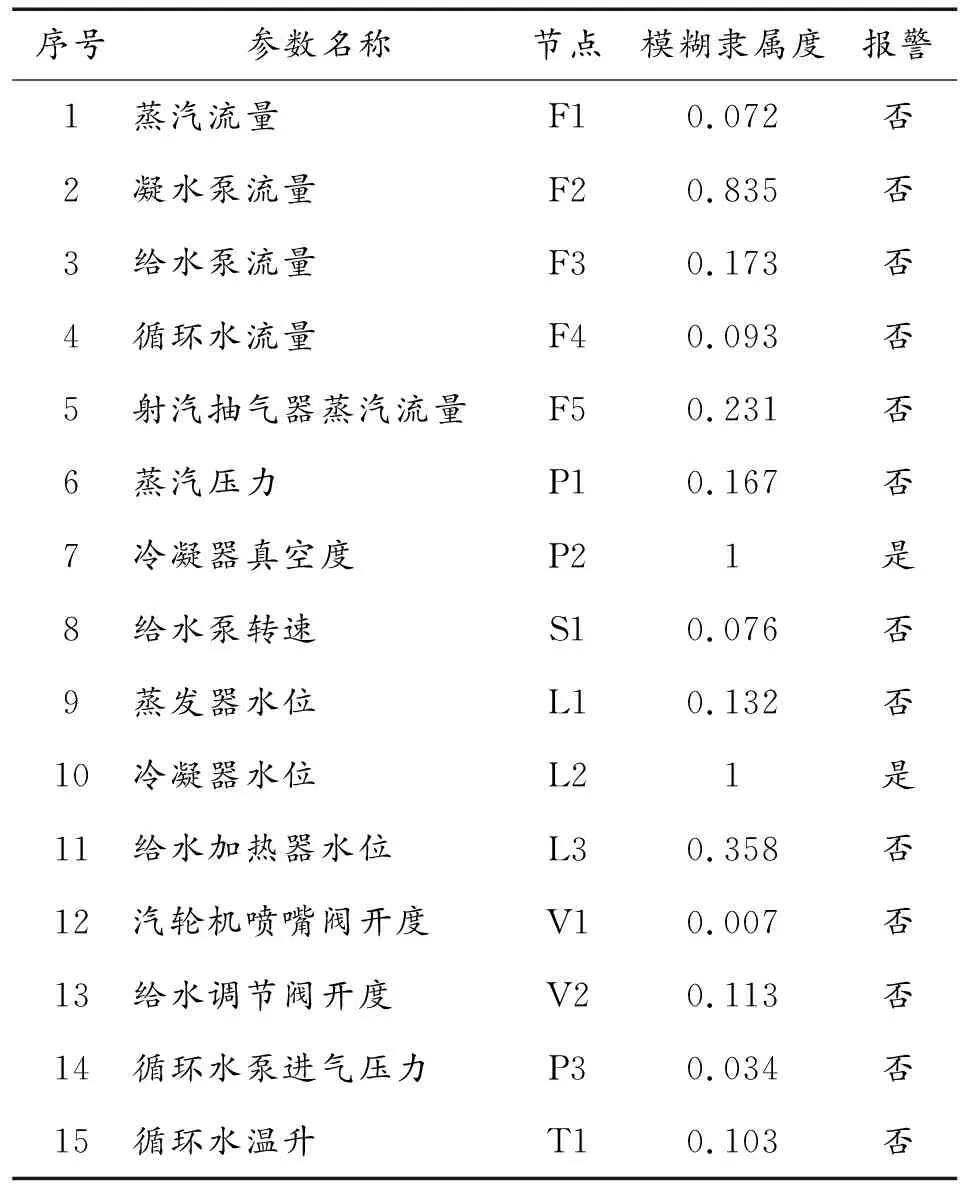
表2 异常状态下瞬时样本数据

故障设置后3 s系统出现报警节点：L2、P2，在图5中用阴影(实际情况为黄色)报警标出。根据分层SDG模型，故障报警只能由高层节点传向低层节点，可以判断故障是从P2以及处在P2所在层以上的节点，通过反向推理得到两条相容通路：

① 冷凝器真空P2(-)冷凝器水位L2(+)蒸汽流量F1(+)喷嘴阀开度V1(+)；

② 冷凝器真空P2(-)冷凝水水位L2(+)冷凝水流量F2(-)

通过分析分层SDG模型中除报警节点以外，相容通路上的节点模糊隶属度：蒸汽流量F1(0.072)、喷嘴阀开度V1(0.007)、凝水泵流量F2(0.835)，可以推断导致冷凝器水位(L2)、冷凝器真空(P2)报警的原因可能是凝水泵故障。通过正向验证凝水泵故障情况下，冷凝水流量降低，冷凝水位升高以及冷凝器真空降低，与监测参数变化一致。

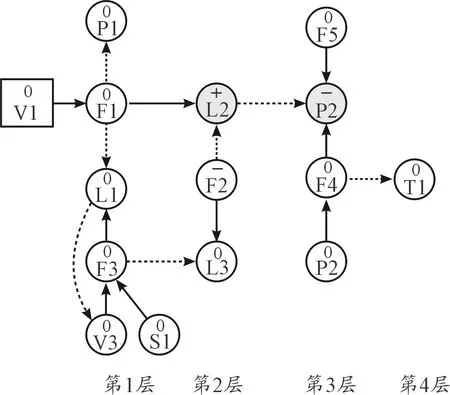
图5 凝水泵停运故障SDG瞬时样本示意图

3.2 冷凝器真空低故障

在核动力装置二回路系统中，冷凝器作为冷源的主要作用，可以将汽轮机高温高压的排汽凝结成水，并在汽轮机排汽口维持一定的真空。循环水泵不断地将冷却水送入冷凝器，汽轮机排汽在冷凝管壁外侧冷凝成水，蒸汽热量通过冷却管壁传递给冷却水。冷凝器真空度是表征冷凝器工作状态的重要参数，如果运行过程中真空度偏低，使汽轮机效率降低，严重时可能导致汽轮机解列。导致冷凝器真空度偏低的原因较多，如射汽抽气器工作不正常、冷凝器冷却管部分铜管堵塞等，需要及时判断并处置。

仿真实验初始条件是核动力装置30%功率运行，在正常运行20 s后减小循环水泵进口阀开度模拟循环水泵故障。根据采集模拟机异常工况下的瞬时样本数据(见表3)，对瞬时样本数据按照线性模糊隶属度算法转换后，得到故障插入后各监测节点的模糊隶属度。

表3 异常状态下瞬时样本数据

本文从图6可以看出，故障设置12 s后，系统出现报警节点：P2、F4，在图6中用阴影，实际情况为黄色报警标出。根据二回路分层SDG模型，可以判断冷凝器真空度低(P2)报警是从P2以及处在P2所在层以上的节点，通过反向推理得到4条相容通路：

① 冷凝器真空P2(-)射汽抽气器流量F5(-)；

② 冷凝器真空P2(-)冷凝器水位L2(+)凝水泵流量F2(-)；

③ 冷凝器真空P2(-)冷凝器水位L2(+)蒸汽流量F1(+)喷嘴阀开度V1(+)；

④ 冷凝器真空P2(-)循环水流量F4(-)。

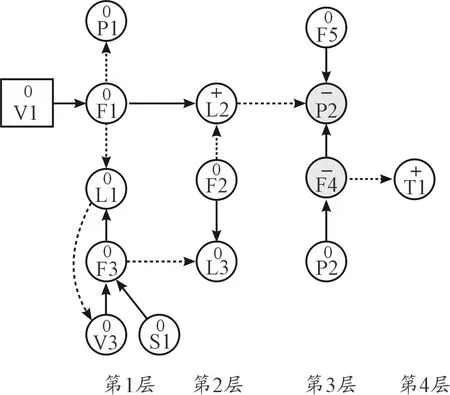
图6 真空度低故障SDG瞬时样本

通过分析分层SDG模型中除报警节点以外，相容通路上的节点模糊隶属度：射汽抽气器流量F5(0.205)、凝水泵流量F2(0.103)、冷凝器水位L2(0.379)、喷嘴阀开度V1(0.009)、蒸汽流量F1(0.072)，可以推断导致冷凝器真空(P2)报警的原因可能是循环水泵故障。通过正向验证循环水泵故障情况下，循环水流量降低，真空度升高，同时循环水温度升高(0.653)与监测参数变化一致。