基于互信息和轮廓系数的聚类结果评估方法

尹世庄，王 韬，谢方方，刘丽君，曲 直，张 斌

(1.陆军工程大学石家庄校区, 石家庄 050003；2.陆军工程大学, 南京 210000)

聚类是一种无监督的学习方法，训练样本没有标签，其聚类结果的好坏难以直接评判[1]。聚类有效性分析主要是研究如何评价得到的不同聚类结果[2]。目前主要有调整兰德系数、互信息评分[3]。针对二进制协议聚类效果评估的研究还比较少，对于未知二进制协议来说，由于其结果正确性无法评判，不能以正确率、识别率、误识别率[4]等指标进行评价。为了解决这一问题，可采用聚类性能度量中的“内部指标”(internal index)进行评判。常用的内部指标有：DB指数(Davies-Bouldin Index,DBI);Dunn指数(Dunn Index,DI)，这两个指数在一定程度上分别反映了簇内距离和簇间距离[5]。显然，DBI越小越好，DI越大越好。本文采用轮廓系数和调整互信息对未知二进制的聚类效果进行评价，调整互信息对聚类结果的簇内距离进行评估，轮廓系数对整体的聚类效果进行评估。

1 相关理论和方法

1.1 聚类性能度量

聚类性能度量也称为聚类的有效性指标，用来评估聚类结果的好坏。从提高聚类精度的角度出发，如果确定了所需要的性能度量，那么我们就可以将该性能度量引入聚类过程中的优化函数，得到更加符合需求的结果。一般来说聚类性能度量可分为两类，分别为外部指标和内部指标。外部指标将聚类结果与某个外部模型进行比较，内部指标则是直接分析聚类结果的本身特性。我们研究的是未知二进制协议，因而采用内部指标。内部指标常用的有DB指数和Dunn指数[6]。DB指数简称DBI，Dunn指数简称DI。分别表示如下；

(1)

(2)

式(1)、(2)中：avg(Ci)代表簇C中所有样本的平均距离；dcen(μi,μj)代表簇Ci和Cj簇的中心点之间的距离；diam(Cl)代表簇C内所有样本之间的最大距离；dijmin代表两个簇Ci和Cj之间最近的样本的距离。

本文采用调整互信息来衡量数据帧之间的相似程度，评估方案中调整互信息值计算的关键代码如表1所示，部分代码省略。labels_true表示获得的第一个聚类中心，labels_pred代表需要分类的数据集，依次计算每一条数据和聚类中心的调整互信息值。其余聚类中心的计算方法与之相同。

表1 计算调整互信息值

1.2 调整互信息

互信息[7](Mutual Information，MI)是反映两个随机变量之间相互依赖程度的一种量度，也称为转移信息(trans information)。是度量两个事件集合之间的相关性(mutual dependence)的一种指标[8]。如果对数以2 为基底，互信息的单位是bit。与相关系数不同的是它的一般性更强，不仅仅适用于实值随机变量。其计算方法如下：

(3)

p(x,y)是X和Y的联合概率密度函数，p(x)和p(y)分别为X和Y的边缘概率密度函数[9]。

从直观上看，互信息代表X和Y之间重叠的信息，也就是说，当知道X或者Y之中任意一个时，另外一个变量的不确定性减少的程度。

调整互信息AMI[10](Adjust Mutual Information)是互信息的一种改进，它能够更好地反映数据分布的吻合程度[11]。

(4)

式(4)中：H(U)和H(V)表示对应样本的边缘熵值；E|MI|表示互信息的期望值。

MI取值范围为[0,1]，但是对于随机结果，MI并不能保证分数接近零。为了解决这一问题，我们引入调整互信息(Adjust Mutual Information)。调整互信息是互信息的一种改进，能够更好地反映数据分布的吻合程度。MI取值范围为[0,1]，AMI取值范围为[-1,1]，它们都是值越大意味着聚类结果与真实情况越接近。

为了检验二进制协议的簇内聚类效果，引入调整互信息，用来衡量两个数据分布的吻合程度，它具有更高的区分度：AMI取值范围为[-1,1]，负数代表结果不好，越接近于1越好。

1.3 轮廓系数

轮廓系数[12](silhouette coefficient)使用数据集中对象之间的相似性度量来评估聚类的质量，是簇的密集与分散程度的评价指标。轮廓系数适用于实际类别信息未知的情况。其计算公式如下：

(5)

式(5)中：a为该数据帧与簇内其他数据帧的平均距离；b为该数据帧与距离它最近的另一个簇中样本的平均距离。

轮廓系数S的取值范围为[-1,1]，S值越大，聚类结果越合理。如果轮廓系数S=-1，则表明该数据帧应该被分到其他的类；如果S接近0，则表明该数据帧在两个类的交叉点上。对全部样本的轮廓系数求平均值就可以得到聚类结果整体轮廓系数sk，即：

(6)

sk的取值范围为[-1,1]，sk值越大，聚类效果越好。

2 聚类效果评估

2.1 K-means改进算法聚类模型

为实现对未知二进制协议的高效聚类，提出了一种基于改进K-means算法的未知二进制协议聚类方法，协议是否已知并不影响聚类的准确度，为了更好地检验聚类效果，故采用已知二进制协议代替未知协议。并且研究对象是已经做了初步切分，协议头部位置确定的比特流(以下均称为未知二进制协议比特流)。以未知二进制协议比特流为输入，输出二进制协议子集。主要分为3个阶段：预处理、确定k值与聚类中心、使用pearson距离的K-means聚类，主要流程如图1所示。首先对数据进行预处理，针对二进制协议的特性，选取了4 bit作为处理单位；处理数据时采用最短数据作为依据进行切割；将每一个单位作为一个特征，得到一个n×m的二维矩阵。再采用DCBP算法、误差平方、进行k值和聚类中心的提取，最后采用改进距离函数的K-means算法对数据进行聚类，将未知二进制协议划分为二进制协议子集。在改进算法中采用Pearson相关性距离作为度量，通过这些改进来提高聚类精度。

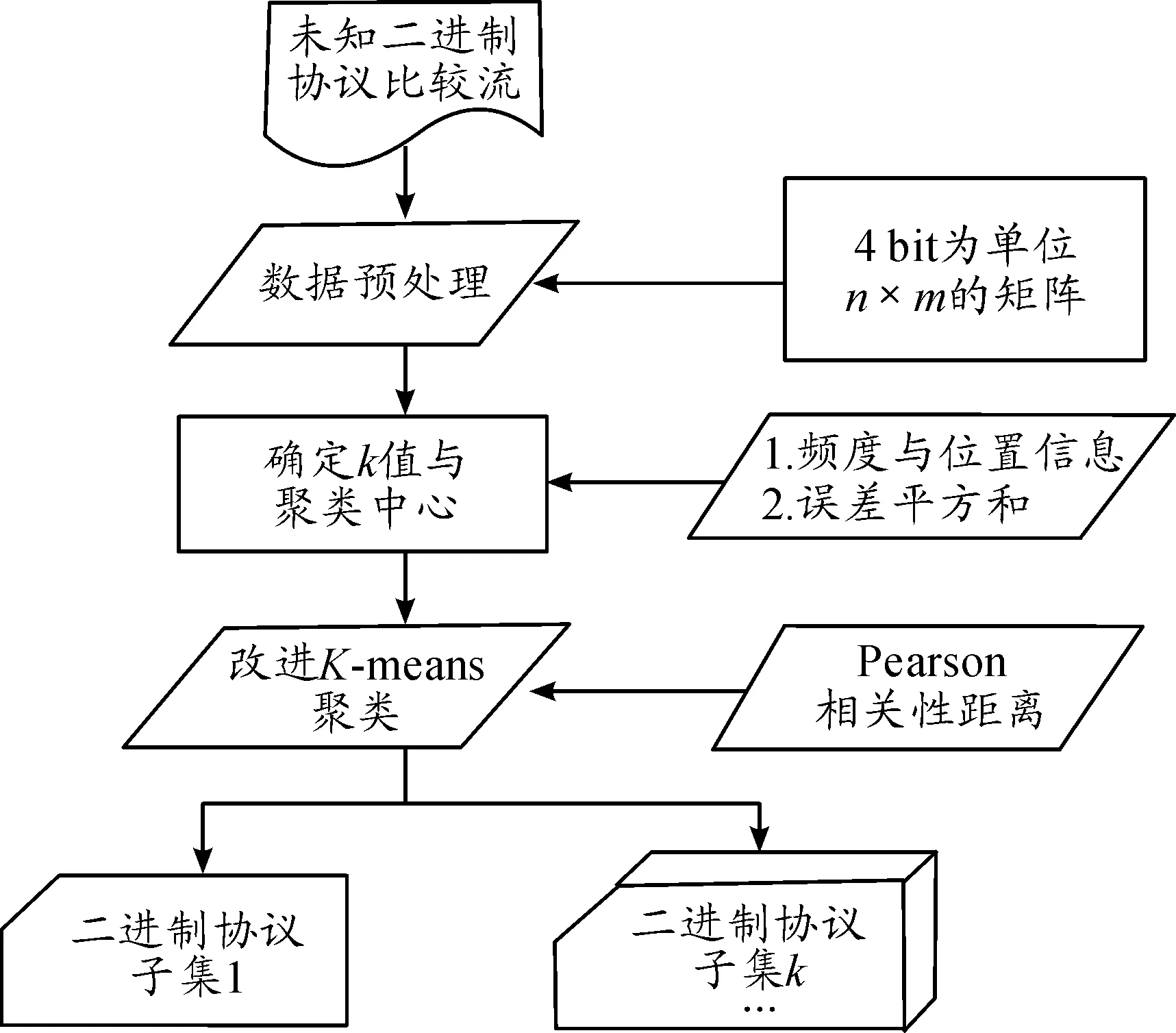
图1 未知二级制比特流聚类实现流程框图

2.2 基于互信息的聚类效果评估

为了检验二进制协议比特流的簇内聚类效果，采用调整互信息来衡量两条数据报文分布的相似程度。调整互信息具有更高的区分度，在聚类结果随机产生的情况下，它的值接近零。AMI取值范围为[-1,1]，负数代表数据报文之间负相关，越接近于1，两个数据报文分布越相近。

定义1类簇的平均调整互信息值f。是指某一聚类中心点到其他样本之间的调整互信息值之和除以样本数n，fmin是指判断是否属于该中心点类簇的最小调整互信息值。

(7)

(8)

在某一类簇中，样本与中心点数据分布的吻合程度越高，调整互信息值越大。设定评价阈值fmin，若样本的调整互信息值大于评价阈值，则判定该样本属于该类簇。在该类簇的所有样本中，正确判定属于该类簇的样本量越大，表示该类簇的聚类效果越好。本文使用正确识别率对结果进行评价。正确识别率[13]是正确识别的目标类和非目标类之和除以总数。其公式为：

(9)

本文提出了一种使用调整互信息的聚类结果评价方案，算法的计算步骤如表2所示。

表2 调整互信息聚类效果评估算法

2.3 基于轮廓系数的聚类效果评估

对聚类效果评估，其实质是对聚类簇进行评估。对簇的评估通常从簇内和簇间两个方面进行,当簇内距离最小和簇间距离最大时，聚类效果最好。簇的凝聚度 (cohesion) 和簇的分离度(separation) 分别对应簇内的紧密程度和簇间的相异程度。Kaufman等[14]提出的轮廓系数结合了凝聚度和分离度。轮廓系数可以对聚类结果的整体有效性进行分析，相关研究可参见文献[15]。

基于轮廓系数的聚类效果评估流程如图2所示。

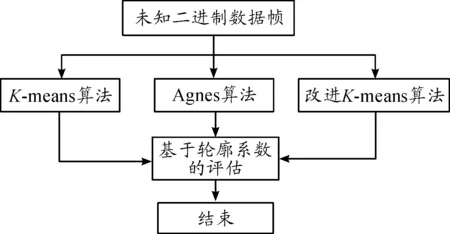
图2 轮廓系数聚类结果评估流程框图

根据不同的数据集，在设定分类数K后，以sk表示聚类轮廓系数。分别采用传统K-means算法、Agnes算法、改进K-means 3种不同算法对相同的数据集进行聚类。通过sk对聚类结果进行有效性分析，找到准确率较高的方法。部分关键代码如表3所示。

表3 轮廓系数评估不同算法的整体聚类效果

3 实验结果与分析

实验数据集由真实网络环境获取，协议是否已知并不影响聚类的准确度，为了更好地检验聚类效果，本文采用已知二进制协议代替未知协议。分别用P1、P2、P3、P4和P5 代表采集的四种未知二进制协议比特流子集：ARP、DNS、ICMP、TCP和SMB，样本量均别为150条。不失一般性，假定所有协议已近做了初步切分，数据报文均从对应协议头部开始并且包含数据部分。取最短数据报文长度144 bit。

为了更好地分析轮廓系数的评估效果，将测试数据分为4组：第一组P1、P2；第二组P1、P2、P3 ；第三组P1、P2、P3、P4；第四组P1、P2、P3、P4、P5。

分别用3种算法对第四组数据进行聚类，最终的聚类结果分布如图3、图4、图5所示。

3.1 互信息效果评估结果与分析

为验证互信息效果评估的有效性，采用改进的K-means算法对第四组数据集进行聚类。通过实验得到五类聚类结果和5个最终的聚类中心。按照调整互信息聚类效果评估算法计算得到各类簇的调整互信息值以及判定属于类簇的样本编号。将得到的结果以样本编号为X轴，到对应聚类中心的调整互信息值为Y轴作图，分析聚类效果的好坏。经过多个数据集大量聚类及评估实验进行总结和比较，可以得出当该类簇中的样本判定的准确率大于90%，则认为聚类效果质量较高。

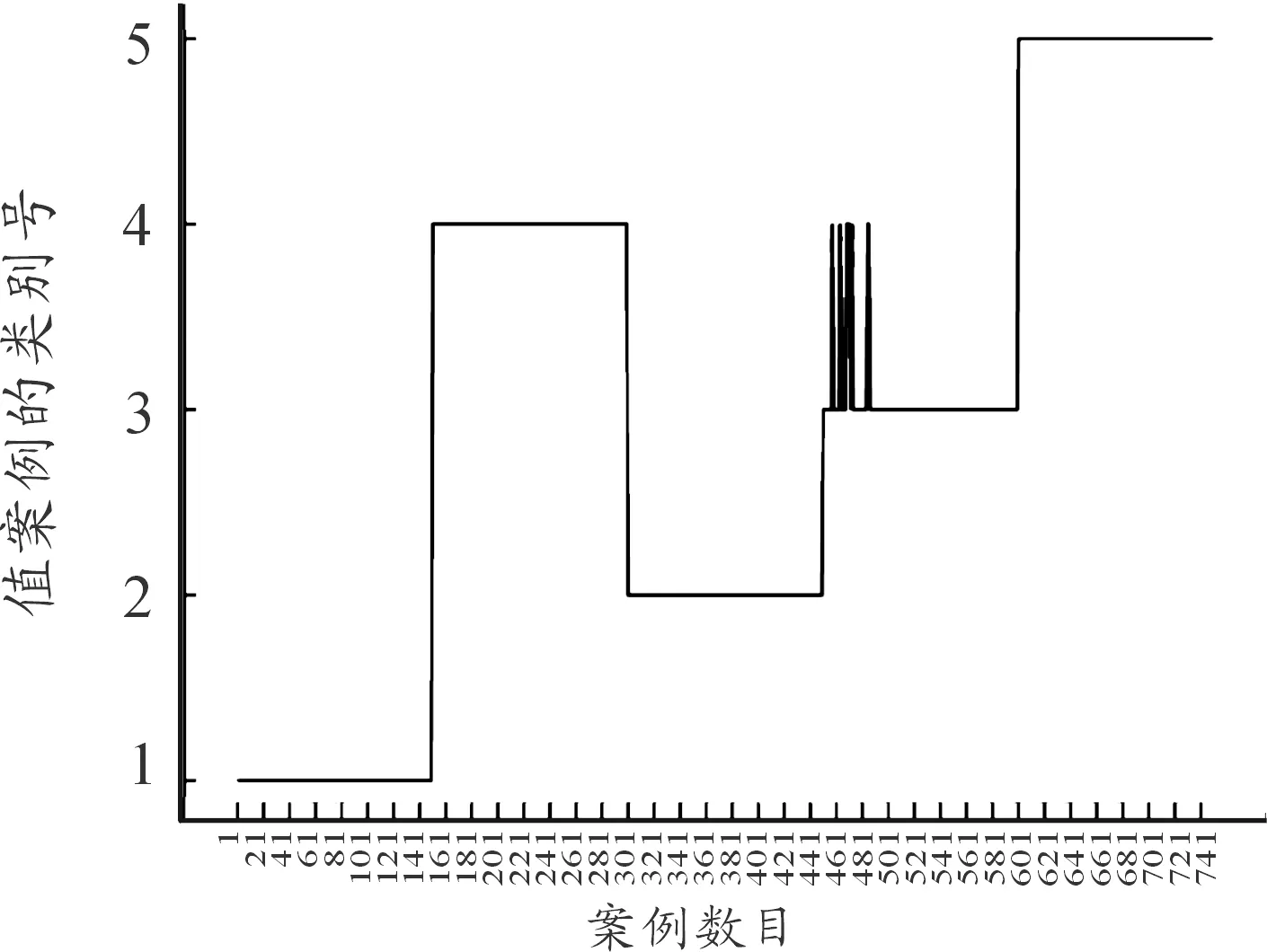
图3 k=5 传统K-means聚类结果分布曲线

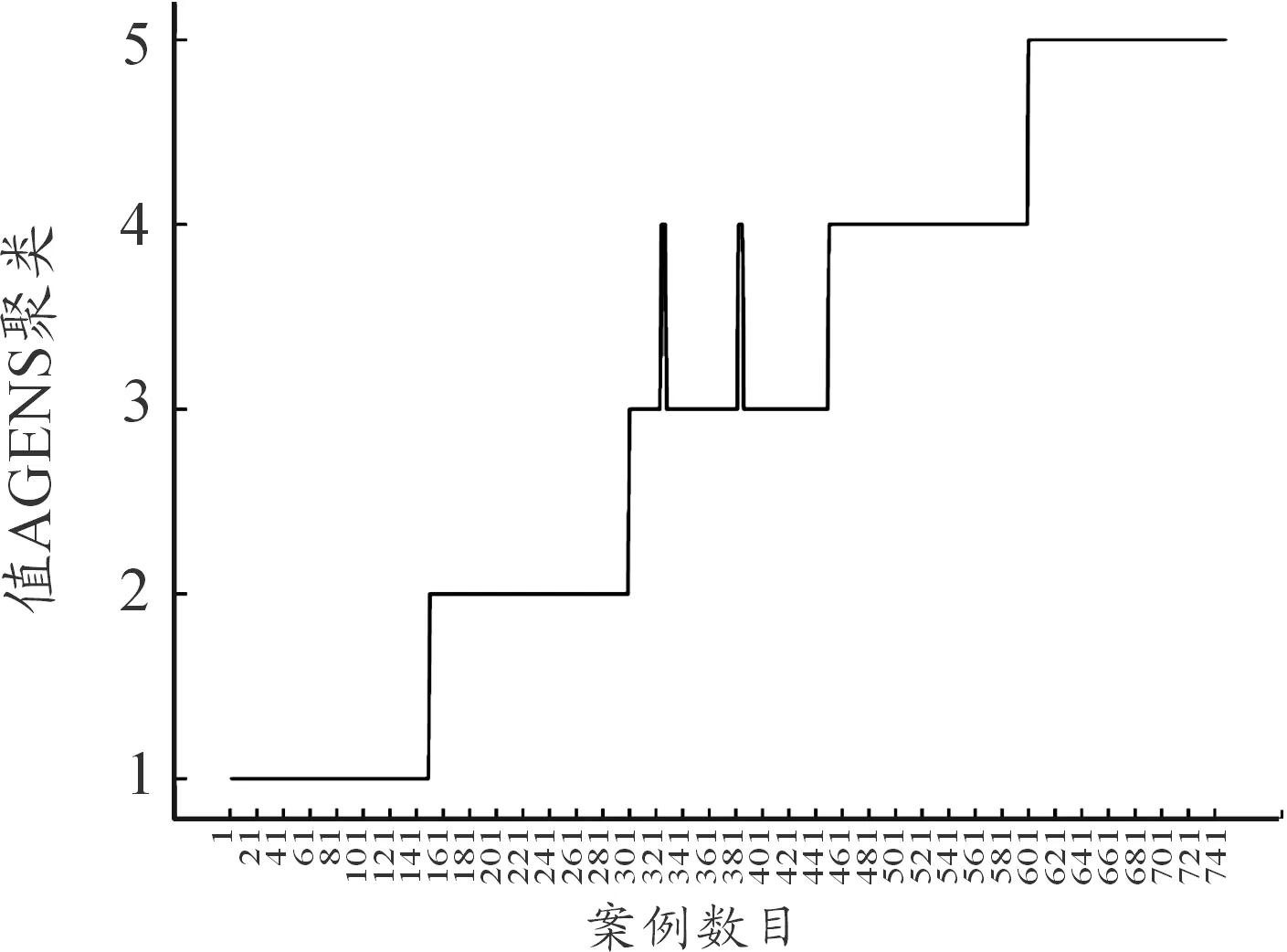
图4 k=5 AGNES聚类结果分布曲线

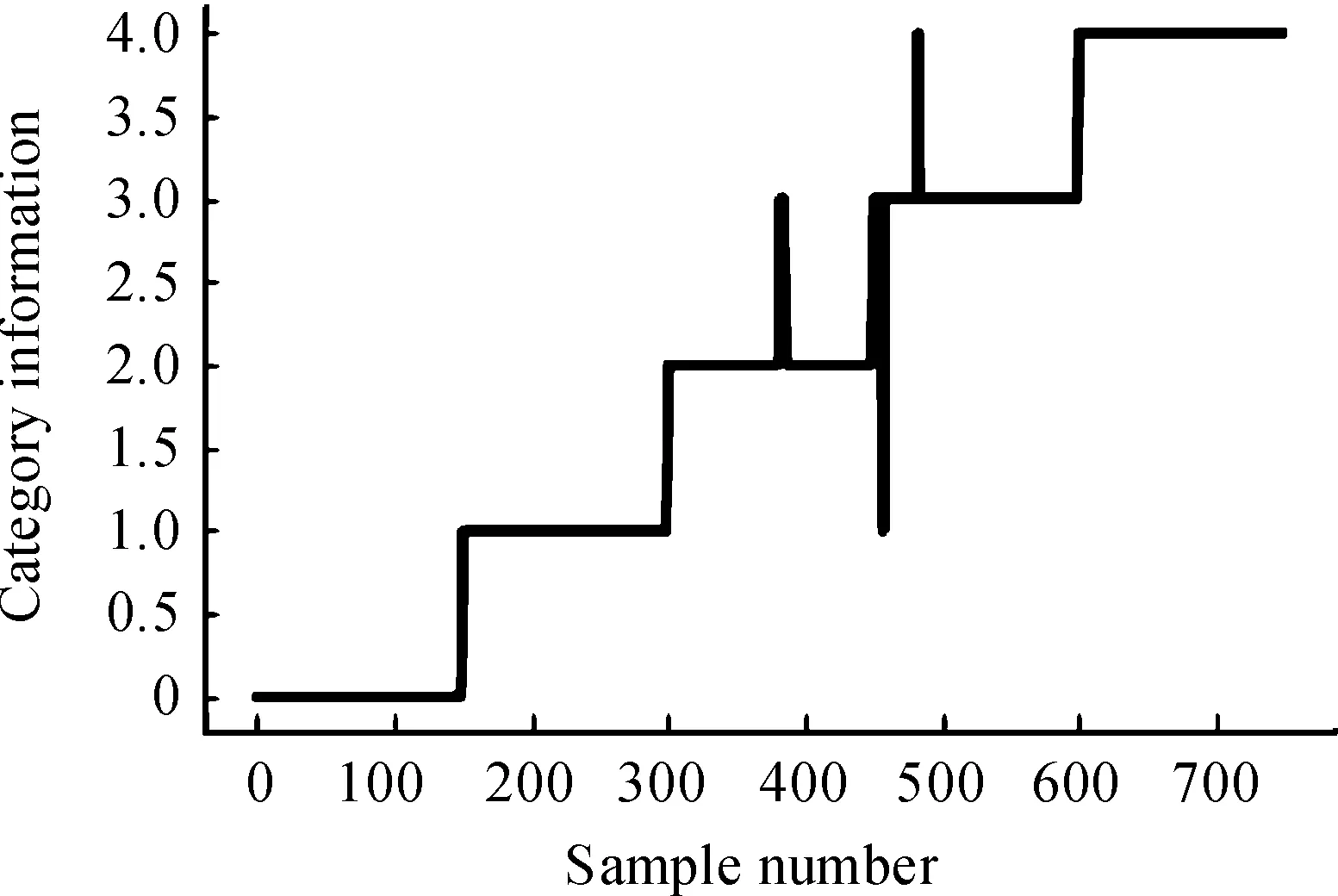
图5 k=5 改进算法聚类结果分布曲线

计算第一个聚类中心与所有样本的调整互信息值，得到的结果如图6(a)所示。图6中x轴是协议编号，y轴是样本与中心的AMI值，反映的是样本随编号的AMI值分布情况。利用第2节定义的公式计算得到fmin=0.269 5，筛选出符合第一个聚类中心条件的样本分布如图6(b)所示。共计150条数据帧被判定为属于该簇。其中全部数据帧判定准确，该类簇中的样本正确识别率为100%。

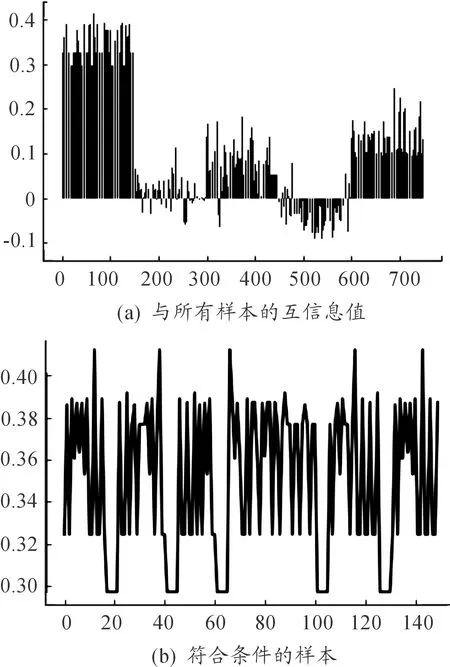
图6 第一个中心互信息效果评估曲线

计算第二个聚类中心与所有样本的调整互信息值，得到的结果如图7(a)所示。利用第2节定义的公式计算得到fmin=0.260 0，筛选出符合第二个聚类中心条件的样本分布如图7(b)所示。共计147条数据帧被判定为属于该簇。其中全部数据帧判定准确，该类簇中的样本正确识别率为99%。

计算第三个聚类中心与所有样本的调整互信息值，得到的结果如图8(a)所示。利用第2节定义的公式计算得到fmin=0.384 8，筛选出符合第三个聚类中心条件的样本分布如图8(b)所示。共计 142条数据帧被判定为属于该簇。其中全部数据帧判定准确，该类簇中的样本正确识别率为100%。

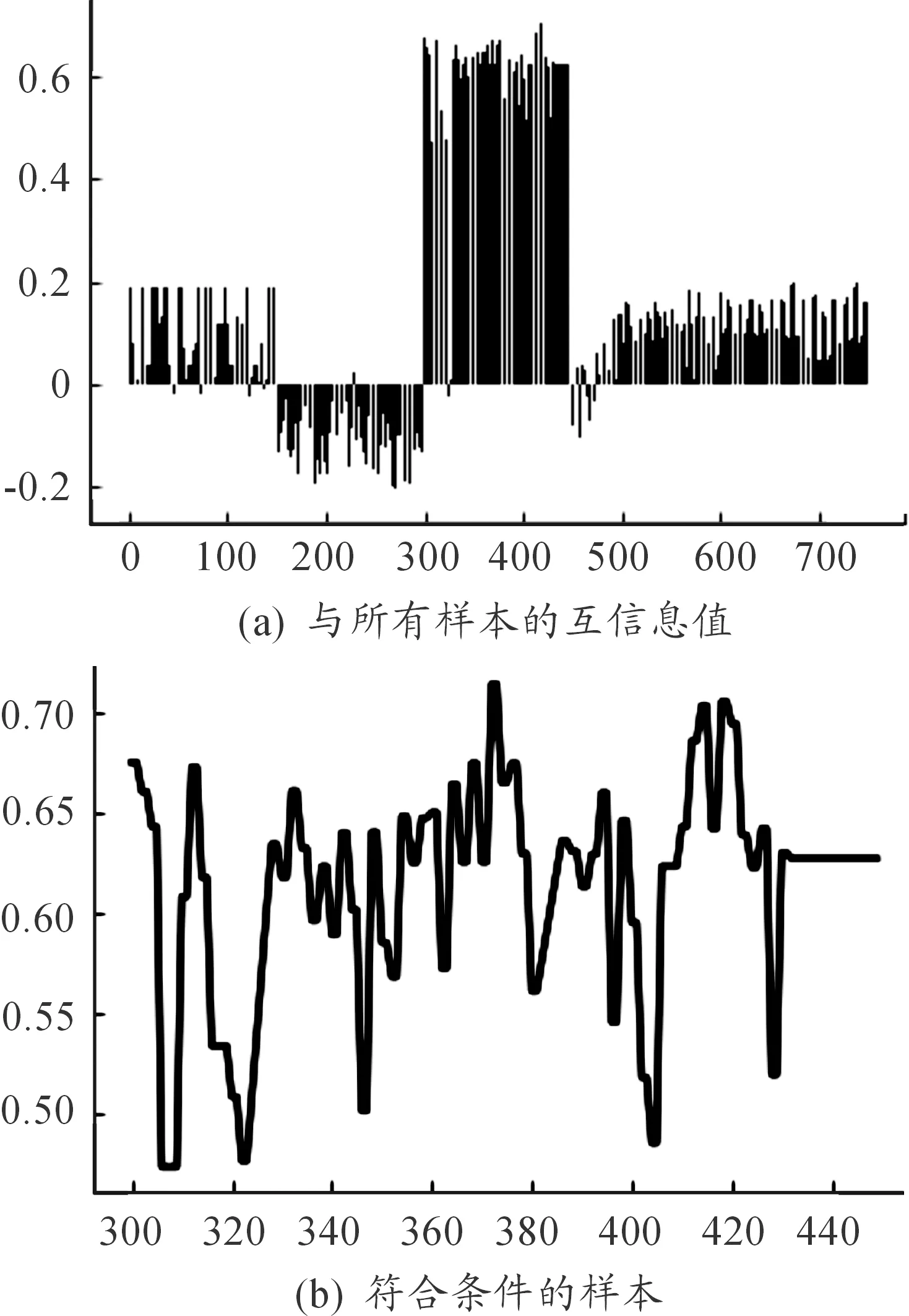
图8 第三个中心互信息效果评估曲线

计算第四个聚类中心与所有样本的调整互信息值，得到的结果如图9(a)所示。利用第2节定义的公式计算得到fmin=0.053 6，筛选出符合第四个聚类中心条件的样本分布如图9(b)所示。共计152条数据帧被判定为属于该簇。其中117条数据帧准确，该类簇中的样本正确识别率为91%。

图9 第四个中心互信息效果评估曲线

计算第五个聚类中心与所有样本的调整互信息值，得到的结果如图10(a)所示。利用第2节定义的公式计算得到fmin=0.270 6，筛选出符合第五个聚类中心条件的样本分布如图10(b)所示。共计 150条数据帧被判定为属于该簇。其中全部数据帧判定准确，该类簇中的样本正确识别率为100%。

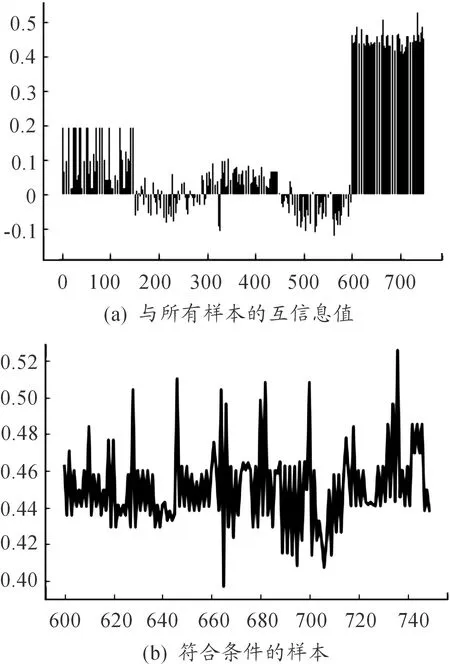
图10 第五个中心互信息效果评估曲线

由于采用已知协议代替未知协议，当k=5时，采用改进的K-means算法对第四组数据集进行聚类，计算得聚类准确率为98.9%，评估方案正确识别率为97.8%。基于调整互信息的聚类效果评估如表4所示，表4中每列数据分别表示聚类后每一种协议所包含的报文条数、调整互信息评估后被判定仍然属于该类的报文条数以及该类簇中的样本被判定为属于该簇的百分比。从数据来看，聚类结果符合评估标准、结果较好。

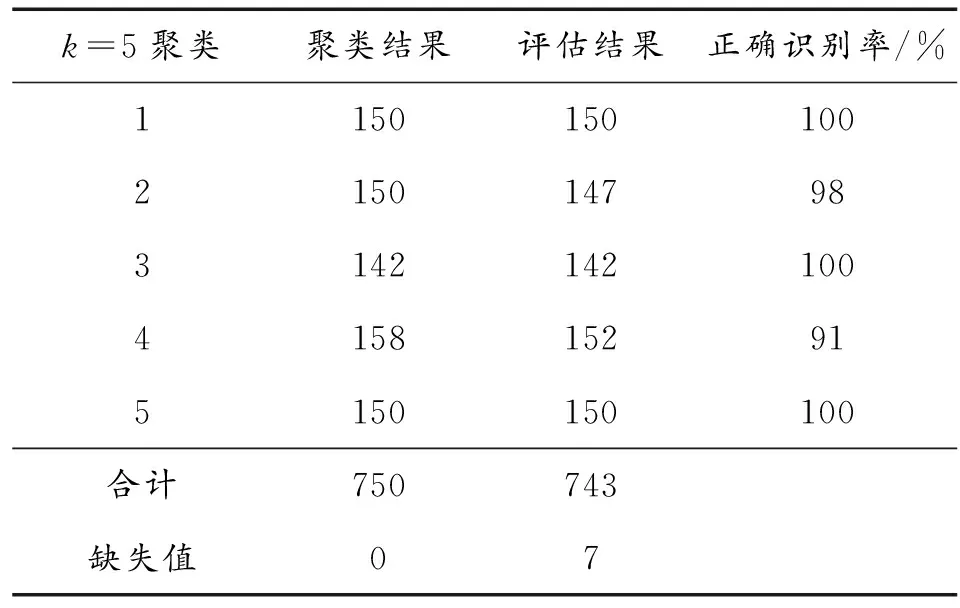
表4 k=5时聚类结果与评估结果

3.2 轮廓系数效果评估结果与分析

实验数据包括第一、第二、第三、第四数据集，对四个数据集采用传统K-means算法、Agnes算法、改进的K-means算法进行聚类。将实验得到聚类结果应用于测试轮廓系数效果评估的有效性。分别计算每种聚类结果的轮廓系数，如表5所示。由于是使用的已知协议类型的数据作为未知协议，因此可以使用精确率进行评价。

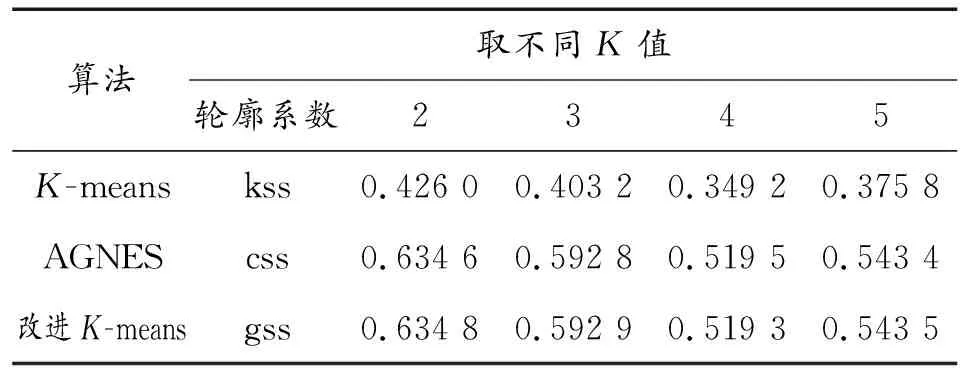
表5 K取不同值时不同算法轮廓系数

如图11所示，改进K-means算法和Agnes算法的聚类效果优于传统K-means。

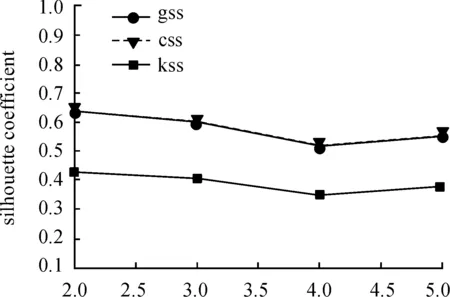
图11 K取不同值时3种算法轮廓系数曲线

表6是采用3种算法分别对4组数据进行聚类后所得聚类结果的精确率。从数据来看改进K-means算法和Agnes算法的聚类效果大致相当，优于传统K-means算法。这与轮廓系数的评估结果是相一致的，因此把轮廓系数作为对聚类结果整体有效性的评估方法是可行的。

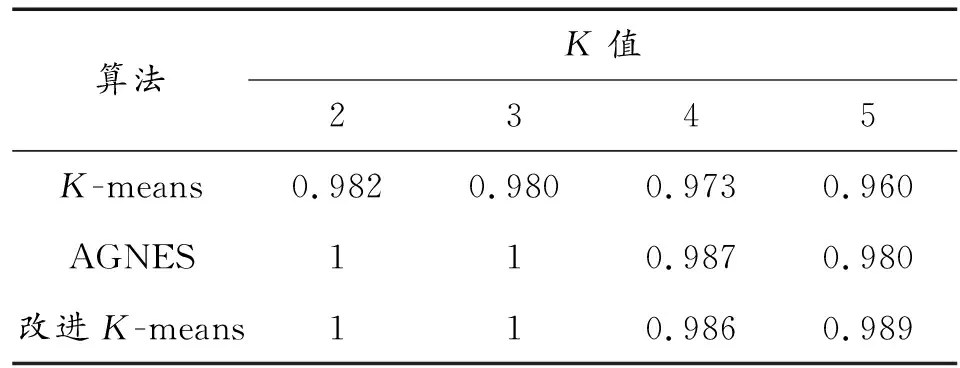
表6 3种不同算法聚类结果精确率

通过对实验结果的分析可以看出,采用互信息和轮廓系数作为二进制协议聚类结果评估的手段是有效的,能够对未知二进制协议的聚类结果进行筛选，找到符合条件的解。

4 结论

未知数据，由于数据特征未知，只能通过“内部指标”衡量，一般是通过簇内距离和簇间距离两个方面进行评估。当簇内距离最小和簇间距离最大时聚类效果最优,本文引入调整互信息和轮廓系数两种参数，分别对聚类的簇内聚类效果和整体聚类效果进行评估。并以真实数据集验证了评估的有效性。与传统评估方法相比，由于采用的是K-means聚类产生的聚类中心，因此评估方法的时间复杂度是O(nt)，优于传统评估方法。

实验发现聚类过程中类簇数目直接影响聚类的精确度。如何确定符合所需粒度的聚类簇需要进一步研究。