基于信息素遗传算法的联合火力打击任务规划
2020-09-07吴世杰
邢 岩,刘 昊,吴世杰
(1.沈阳航空航天大学 电子信息工程学院, 沈阳 110000; 2.国防大学联合作战学院, 石家庄 050000;3.辽宁省军区, 沈阳 110000)
联合火力打击作为联合作战的重要组成部分,是形成和发挥诸军兵种火力打击部队综合作战效能的实践环节,对联合火力打击的任务规划优劣直接影响诸军兵种火力打击部队作战能力的发挥,也是联合作战筹划中的重点和难点[1]。军事运筹学已经对火力打击任务规划中的动态火力分配问题进行深入系统的研究,并证明其属于NP完全问题,联合火力打击任务规划在原有动态火力分配基础上,引入了多兵器、多弹种维度变量,各约束条件相互牵制,使问题复杂度进一步提升[2]。对于NP完全问题的求解,通常使用智能优化算法通过多代演化获取具体问题的可行解,并通过对算法的改进试图在有限代数内使可行解逼近全局最优,然而对智能优化算法的设计和改进方案仍处于探索阶段。
自1972年遗传算法被提出并应用于NP问题求解后,众多原理不同、功能和设计理念各异的智能优化算法相继被提出,代表算法包括以模拟生物群体行为特征的蚁群算法[3]、蛙跳算法[4]、蜂群算法[5]、粒子群算法[6]、布谷鸟算法[7]、萤火虫算法[8]、鱼群算法[9]等;以模拟自然现象的模拟退火算法[10]、量子进化算法[11]、细胞膜优化算法[12]等;以模拟生命演化规律的遗传算法[13]、人口迁移算法[14]等。各种智能优化算法的设计原理和依据各异,在解决具体问题方面各具优势,特别是遗传算法作为最早提出的智能优化算法,因其构造简单,优化效果明显,成为应用最广泛的智能优化算法。然而遗传算法也存在如下问题:一是易陷入局部最优陷阱。当进化到一定代数时,受限于最优个体的自身结构,导致算法无法寻找到全局最优。二是进化代数不可控。不论算法的结束条件如何限定,都难以保证评分收敛和代数可控之间的平衡,使算法实效性有所降低。基于此,本文借鉴了蚁群算法中的信息素浓度概念,将其引入到遗传算法的变异环节,实现可控性变异,以此提升算法收敛效率,并通过寿命条件和轮盘法的综合运用,提升算法全局寻优能力,将信息素遗传算法应用于联合火力打击任务规划具体问题中,取得了良好的优化效果。
1 问题描述
联合火力打击任务规划中的兵力、火力和目标之间的动态分配问题是典型的NP完全问题,包含了使目标火力毁伤份额达成情况下,必须满足兵力、弹药损耗最优化等约束条件。设我方参与联合火力打击的部队为B={b1,b2,…,bn},其中bk表示第k支部队的数据输入变量集合;敌方目标打击清单中的目标为D={d1,d2,…,dm},其中dl表示第l个目标的数据输入变量集合;设联合火力打击任务规划中,第k支部队对第l个目标实施火力打击时,H表示毁伤程度,G表示火力打击任务份额,L表示消耗弹药总量,Ts和Tz分别表示火力打击起始和结束时刻,Tk表示第k支部队的火力打击总时长。设计联合火力打击任务规划的硬约束条件如下:
1) 任务规划必须完成上级分配的各目标火力打击任务份额。设任务规划中的子任务数为p个,则约束条件数学模型如下:
(1)
2) 任务规划必须确保各火力打击部队留存弹药完成临机任务。设每次火力打击的弹药消耗量为li,则约束条件数学模型如下:
(2)
3) 任务规划必须确保各火力打击任务在上级规定时限内完成。约束条件数学模型如下:
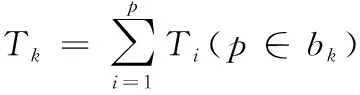
(3)
max{T1,T2,…,Tk}≤Tz-Ts
(4)
在满足硬约束条件基础上,联合火力打击任务规划还应满足如下软约束条件:
1) 突然性原则。火力打击的持续时间尽可能短,保证火力打击发起的突然性。
2) 损耗性原则。火力打击部队的兵力和弹药损耗尽可能低,保证留存足够兵力和弹药完成临机任务。
3) 平均性原则。火力打击部队担负的任务量尽可能平均,保证各子任务平行展开,分担压力。
4) 一致性原则。任务规划的总体火力打击时长尽可能和上级规定的火力打击开始、结束时限保持一致,保持持续的火力威慑效能。
5) 复合毁伤原则。由于对同一目标的多弹种打击会造成高于单一弹种打击造成的毁伤,任务规划尽可能保证同一时刻多弹种对同一目标达成毁伤。
经过上述分析,归纳联合火力打击任务规划的难点为:一是联合火力打击的参战军兵种多、弹种多、精确制导弹药和范围毁伤弹药并存、各火力打击子任务互相牵制,使综合评分计算难度大幅提升;二是任务规划必须留足兵力和火力应对临机火力打击任务,规划任务和临机任务的分配比例难以确定;三是任务规划的优化只适用于当前敌我态势,如何随敌我态势动态变化而修订调整任务规划也是联合指挥员面临的工作难点。
2 算法构建
信息素遗传算法的内核仍然是智能优化算法,将智能优化算法应用于联合火力打击任务规划等NP完全问题的算法设计步骤可分为数据录入阶段、向量空间转换阶段、综合评分阶段、智能优化阶段。其中,数据录入阶段用于将联合火力打击任务规划的具体数据指标录入计算平台;向量空间转换阶段用于将联合火力打击任务规划中的兵力、火力、目标规划问题转换为多维向量空间中寻找全局最优位置问题,将代数问题转换为几何问题;综合评分阶段用于构建联合火力打击任务规划的综合评分模型,通过录入的数据计算当前任务规划下的综合评分;智能优化阶段以综合评分模型为基础,通过智能优化算法在多维空间中构建众多随机个体,通过个体的随机游走或变异寻找周边最优综合评分,并在多代进化后输出最优个体综合评分。智能优化算法的流程如图1所示。

图1 智能优化算法流程框图
2.1 信息素遗传算法
遗传算法是借鉴自然界的生物进化过程,模拟优胜劣汰和适者生存的竞争淘汰机制设计的智能优化算法,以伪随机数模拟个体的变异过程,通过多代进化使最优个体综合评分向全局最优评分收敛。标准遗传算法的流程如图2所示。
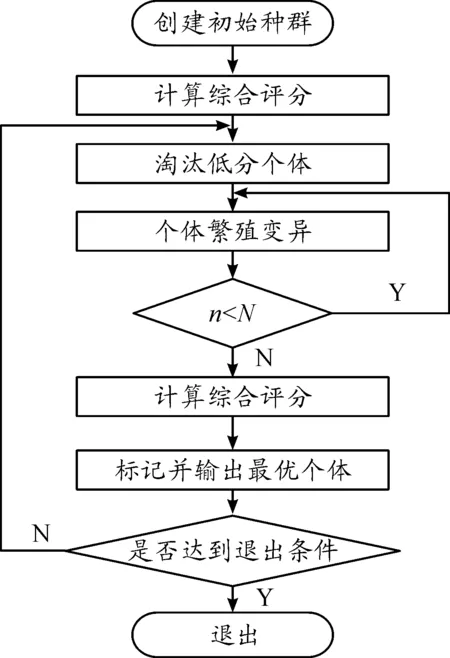
图2 标准遗传算法流程框图
蚁群算法是M Dorigo等在1991年提出的智能优化算法,算法原理为:蚁群在觅食过程中会随机遍历所有路径,并沿途释放随时间递减的信息素,蚁群后续跟进的蚂蚁个体则根据信息素浓度判断哪条路径经过的蚂蚁多,并释放信息素强化已遍历路径,经过多次迭代,越短的路径信息素浓度就越高,浓度上升又会使后续蚁群选择该路径的几率增大,最终使蚁群按照最优路径找到食物。在蚁群算法中,信息素浓度能够强化变异的正反馈循环,提升变异效率,缩短进化的迭代次数,因此考虑将信息素浓度引入到遗传算法中,设计信息素遗传算法。具体算法为:
步骤1:初始化种群。生成信息素浓度数组和禁忌表数组。
步骤2:创建个体。定义个体的数据结构如表1所示。

表1 个体数据结构
步骤3:计算种群综合评分。将种群中的个体对应的任务规划代入综合评分算法中计算个体的综合评分。
步骤4:种群灭绝。按照种群淘汰比例将种群规模压缩,使用轮盘法选择应保留的个体,保证高评分个体留存概率较大,低评分个体也有留存机会;所有留存个体的寿命+1。
步骤5:种群繁殖变异。使用轮盘法选择繁殖的父代个体,按照禁忌表的选择方向产生变异,同时根据禁忌表更新信息素数组中的浓度系数,没变异的禁忌方向浓度递减,产生变异的禁忌方向浓度递增,使种群规模达到上限。设任务规划子任务的目标序号为i,部队序号为j,τij表示第j支部队打击第i个目标子任务的信息素浓度,ηij表示子任务综合评分,α和β为重要程度参数,K表示禁忌表数组集合,则变异方向概率pij计算公式为:
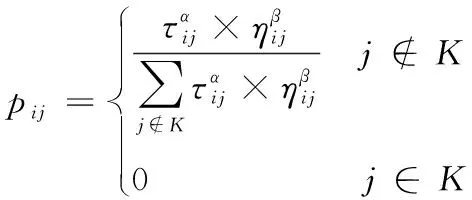
(5)
步骤6:重复步骤3~5,并记录每次进化的最优个体综合评分。
步骤7:判断退出。若达成退出条件,则退出算法并输出最优个体及综合评分。算法流程如图3所示。
2.2 评估指标算法
根据联合火力打击任务规划问题软硬约束条件的分析,可将任务规划的综合指标区分为单目标类评估指标、单部队类评估指标和体系评估指标3类。单目标类评估指标的数量和目标数等同,单部队类评估指标的数量和部队数等同,体系评估指标和任务规划数等同。并基于3类评估指标设计11项具体指标,评估指标明细如图4所示。

图3 信息素遗传算法流程框图

图4 联合火力打击任务规划评估指标框图
设联合火力打击部队数为n,其中第i支部队的火力打击半径为oi,在任务规划中能够执行打击任务上限为ci,单次火力打击时长为di,火力打击之间的转换周期为ei,部队位置坐标为xmi和ymi;目标打击清单中的目标数为m,其中第j个目标的规定毁伤程度为hj,目标位置坐标为xnj和ynj,对目标造成压制毁伤对应的火力打击次数为g40j,对目标造成歼灭毁伤对应的火力打击次数为g60j;联合火力打击任务规划中共包含子任务数为r,其中第k个子任务的对应火力打击次数为lk,火力打击起始时刻为pk,结束时刻为qk;执行该火力打击后的部队兵力损耗比例为u。计算评估指标前要对子任务进行可行性判断:
1) 去除超程子任务,计算公式为:

(6)
2) 去除超过部队火力打击次数上限的子任务,计算公式为:
(7)
而后依次计算各项评估指标:
1) 单目标火力打击时长(Aj)。代表对第j个目标实施火力打击的总用时,计算公式为:
Aj=max{qj}-min{pj}
(8)
2) 单部队火力打击次数(Bi)。代表第i支部队在任务规划下执行火力打击的总次数,计算公式为:
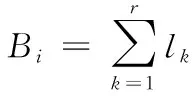
(9)
3) 火力打击整体时长(C)。代表执行任务规划各火力打击任务的总用时,计算公式为:
C=max{qk}-min{pk}
(10)
4) 单目标冗余弹药比例(Ej)。代表对第j个目标实施火力打击分配的弹药超过标准投放弹药的比例。设投放弹药比例为Dj,s表示目标等级,d表示部队的火力打击次数,计算公式为:
(11)
Ej=max{0,Dj-100}
(12)
5) 单目标完成任务比例(Fj)。代表对第j个目标实施火力打击后,造成的毁伤份额占规定毁伤份额的比例,计算公式为:
Fj=min{100,Dj}
(13)
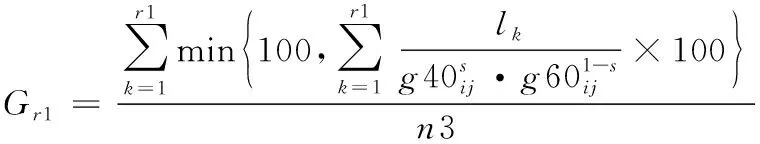
(14)
7) 防空预警削弱能力(Hr1)。代表在完成任务规划中第r1个子任务时,对敌防空预警能力的削弱程度,计算公式为:
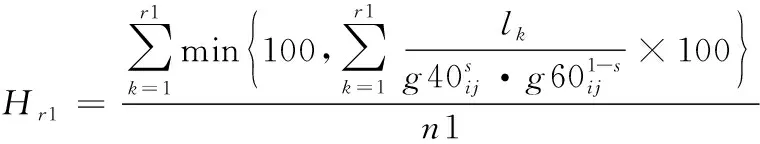
(15)
8) 地面打击削弱能力(Ir1)。代表在完成任务规划中第r1个子任务时,对敌地面远程打击能力的削弱程度,计算公式为:

(16)
9) 弹药剩余比例(Ji)。代表第i支部队完成所有火力打击任务后剩余的弹药占原有弹药的比例,计算公式为:
(17)
10) 兵力剩余比例(Ki)。代表第i支部队完成所有火力打击任务后剩余的兵力占原有兵力的比例,计算公式为:
(18)
11) 复合打击次数(L)。代表对同一目标的多弹种立体交叉火力打击的发生次数,计算公式为:
(19)
(20)
2.3 综合评分算法
针对联合火力打击任务规划问题中的评估指标众多、评估分值差异较大的情况,本研究借鉴了标准熵权法与理想点法,设计使用熵权理想点法对11类联合火力打击任务规划的评估指标进行降维,并融合输出为可量化比较的综合评分。熵权理想点法的设计思路为:首先使用熵权法将各目标和各部队的子类评估指标按照目标和部队的分类计算熵权,并加权求和计算出单目标类中的3项评估指标和单部队类中的3项评估指标;而后计算5项体系评估指标;最后使用理想点法对11项已经量化梳理好的评估指标进行理想点位空间距离计算,形成量化可比的综合评分。熵权理想点法规避了复杂系统建模中评估指标过细、层次过多等问题,将复杂系统中的各类评估指标区分层次加以实施分步融合,使得综合评分更加客观可信,特别适用于解决复杂系统建模中的多指标量化评估问题。
使用熵权法[15]将单目标类评估指标和单部队类评估指标融合为单一分值。设联合火力打击任务规划中,共有m个火力打击目标,n个任务规划参与综合评分,则构建矩阵X,熵权法融合的计算流程如下:
步骤1:归一化计算。将矩阵X转换为归一化矩阵P,计算公式为:
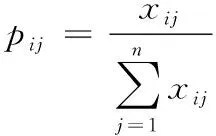
(21)
步骤2:熵值计算。通过归一化矩阵P计算m个目标的对应熵值ej,计算公式为:
柑桔红蜘蛛的防治是赣南脐橙病虫害防治中一项很重要的工作。柑桔红蜘蛛一年代数很多,为害大。为提高脐橙的产量与质量,柑桔红蜘蛛防治工作必须持之以恒。
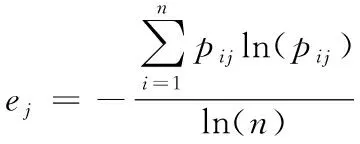
(22)
步骤3:熵权计算。通过熵值ej计算m个目标对应的熵权重tj,计算公式为:

(23)
步骤4:融合分值计算。通过熵权重tj和矩阵X计算各任务规划的融合分值zi,计算公式为:
(24)
获取11项评估指标后,建立n个任务规划的评估指标矩阵Z,使用理想点法[16]将各评估指标融合为单一的综合评分,理想点法的计算流程如下:
步骤1:理想点计算。通过矩阵Z获取正负理想点A+和A-,计算公式为:

(25)

(26)
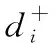
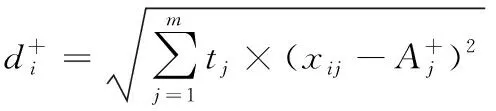
(27)
(28)
步骤3:综合评分计算。通过理想距离计算综合评分,计算公式为:

(29)
3 仿真分析
为了验证信息素遗传算法应用于联合火力打击任务规划的适用性,采用文献[13]中提供的标准遗传算法作为参考算法,设计综合评分算法。仿真实验平台配置为:Intel酷睿双核处理器T7300 2.0GHz;3G内存;Window 7 32位操作系统;VC6.0编程环境。为了检验算法应用于联合火力打击任务规划的合理性,设置我方火力打击部队的兵力配置如表2所示。
敌方目标的属性及打击毁伤情况如表3所示。

表3 目标属性及打击毁伤情况(简略)
3.1 参数有效性分析
首先通过仿真实验修正信息素遗传算法的各项输入参数,确保算法达到最优效果。通过算法分析,引入参数如下:种群规模、变异概率、信息素更新系数、淘汰比例、寿命上限、进化退出代数。参数有效性实验步骤为:
步骤1:为所有参数输入初始值;
步骤2:以某一参数为调整对象,在取值范围内微调;
步骤3:计算参数设置条件下的算法综合评分;
步骤4:重复步骤2~3,直至找到某一参数的最佳参数值;
步骤5:重复步骤2~4,直至找到所有参数的最佳参数值。
需要注意的是,调整参数初始值后,需要重新微调各参数值,否则综合评分不准确。通过仿真实验,确定信息素遗传算法的参数有效性指标如表4所示。

表4 参数有效性指标
3.2 综合评分对比
为了验证信息素遗传算法的优化性能,以标准遗传算法为参考算法设计仿真实验如下:
步骤1:初始化算法环境,设置进化次数均为300代;
步骤2:将算法代入联合火力打击任务规划问题,计算各代个体综合评分;
步骤3:标记算法全局最优个体和各代最优个体的综合评分;
步骤4:输出结果。
算法全局最优个体综合评分和各代最优个体综合评分情况如图5和图6所示。
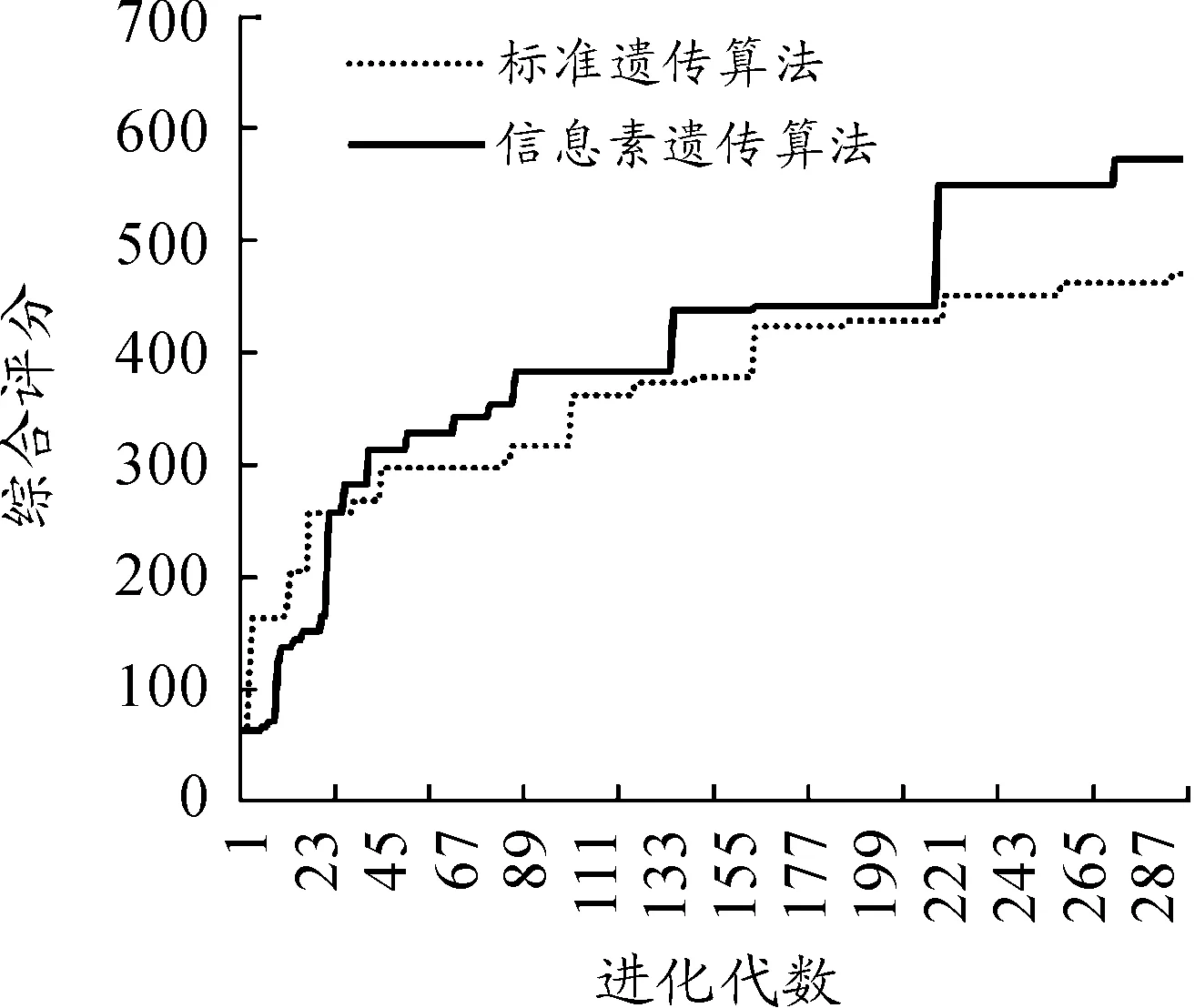
图5 全局最优个体综合评分曲线
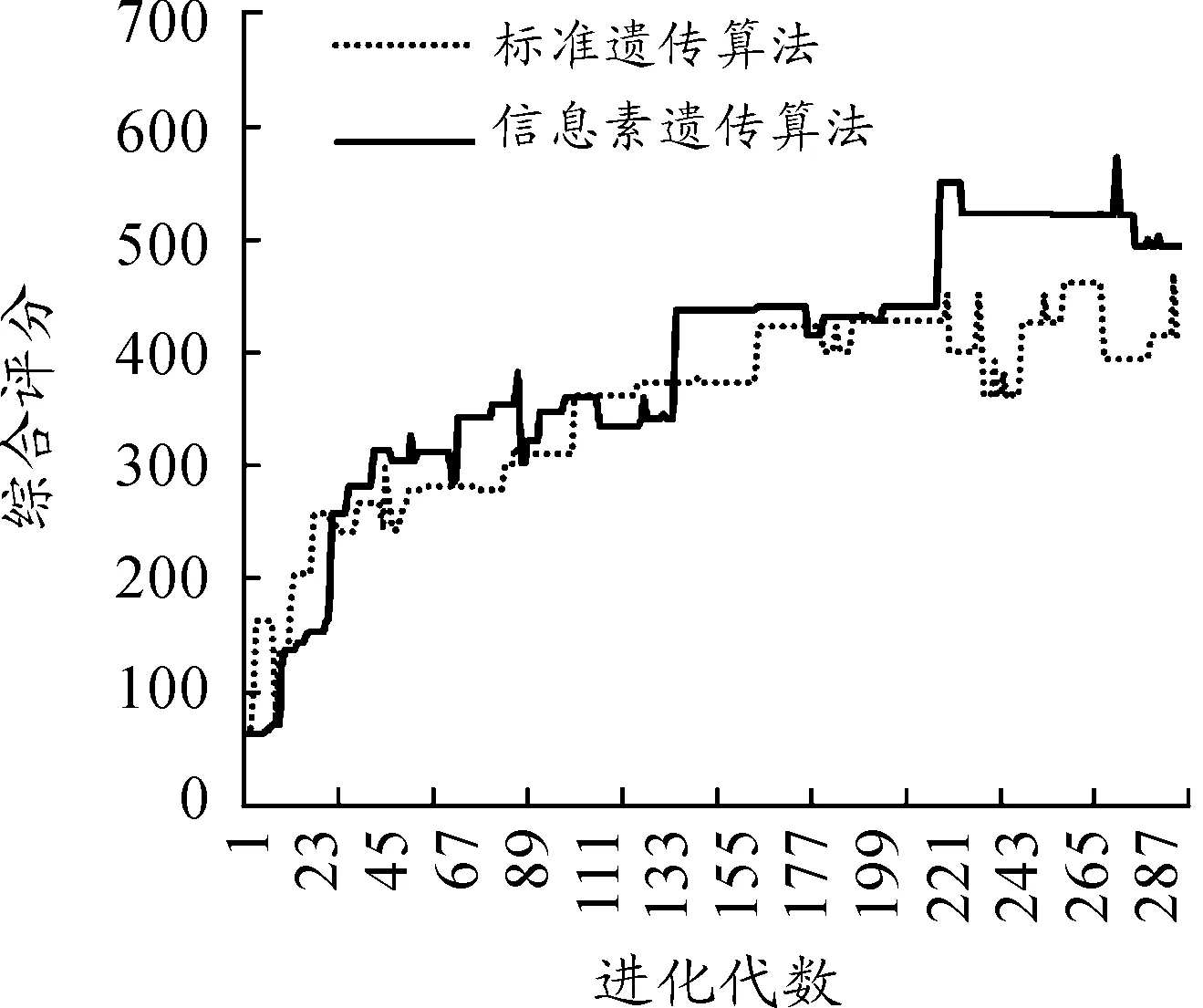
图6 各代最优个体综合评分曲线
实验结果表明:信息素遗传算法的收敛效率明显高于标准遗传算法,这主要是由于引入信息素浓度对变异方向进行了自动控制,算法会自动向高分变异方向倾斜。此外,信息素遗传算法的综合评分高于标准遗传算法,这主要是由于信息素遗传算法引入了寿终正寝和轮盘法选取下一代繁殖个体,使种群的多样性相较于标准遗传算法更高,全局寻优能力更强。
3.3 最优个体对比
为了验证信息素遗传算法获取的全局最优个体性能,以标准遗传算法获取的全局最优个体作为参考对象,分析比较两种个体的获取时间、进化代数以及个体内各评估指标的情况。两种算法最优个体的获取时间如图7所示,完成算法的进化代数如图8所示。
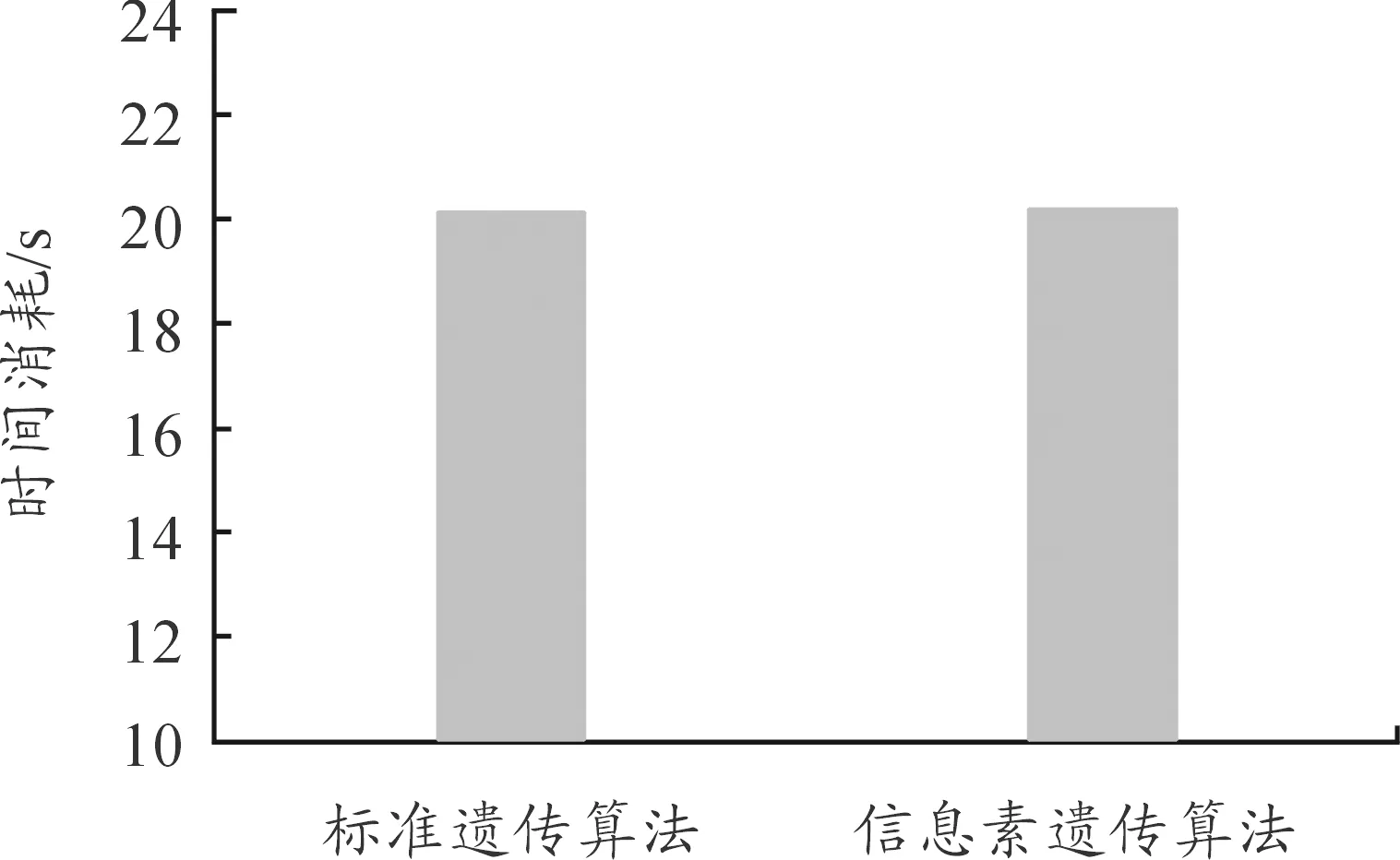
图7 最优个体获取时间图
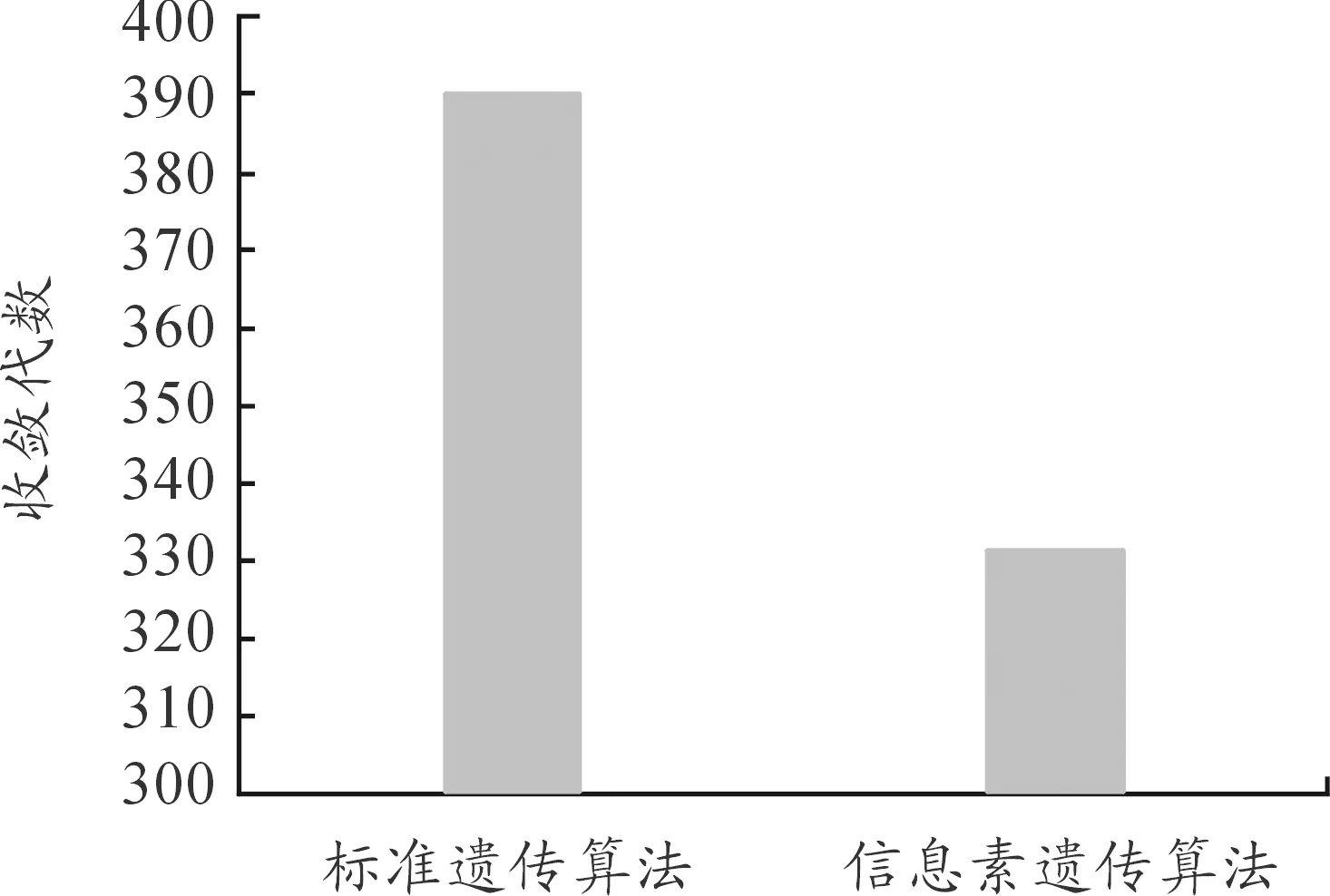
图8 进化代数图
实验结果表明,信息素遗传算法最优个体具有更短的收敛时间和更低的收敛代数,算法效率明显高于标准遗传算法,具有更好的工程应用前景。对两种算法最优个体各项评估指标如图9所示。
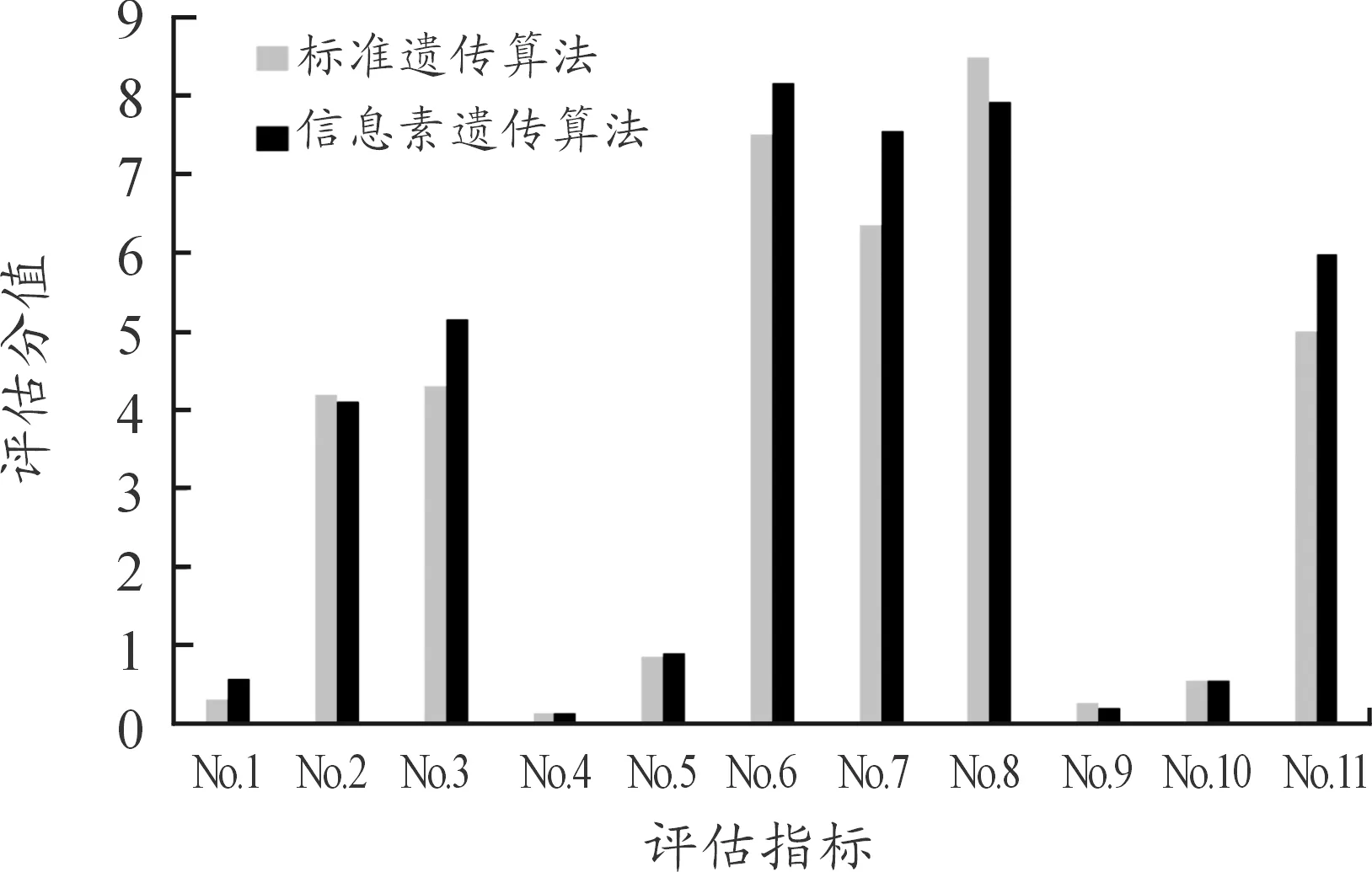
图9 最优个体各项评估指标分值图
实验结果表明,信息素遗传算法的各项评估指标与标准遗传算法最优个体相差不大,其中单目标完成任务比例(No.3)和复合打击次数(No.11)评估指标要明显高于标准遗传算法最优个体,综合评分则略有提升,由此可以判断,标准遗传算法获取的最优个体并非全局最优。最优个体对应的联合火力打击任务规划示例的突击时间如表3所示。
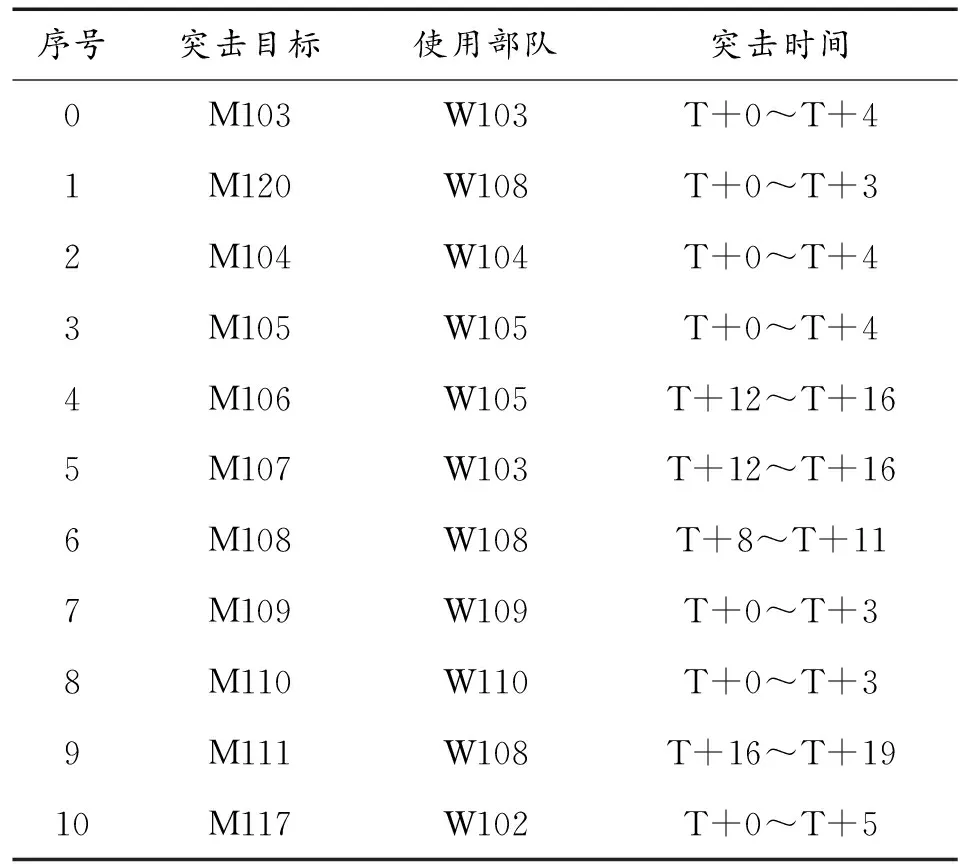
表5 联合火力打击任务规划示例的突击时间
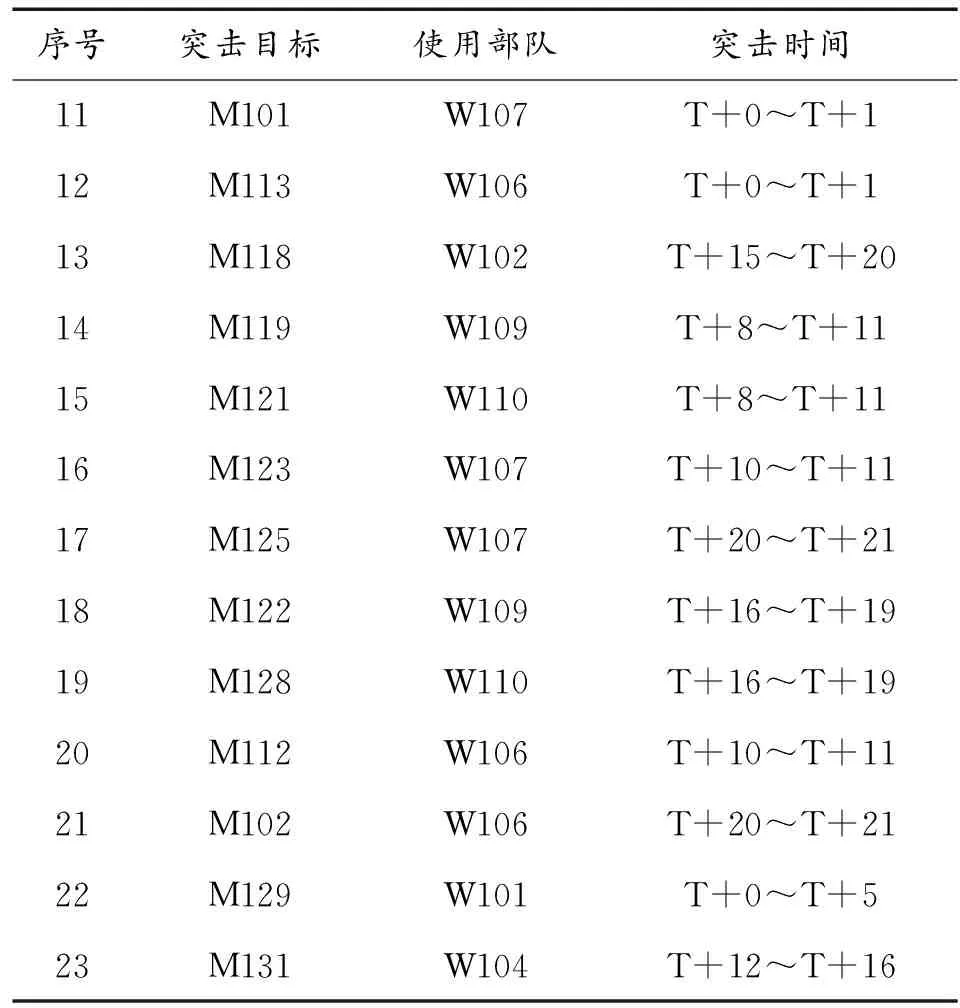
续表(表5)
4 结论
1) 构建了能够量化比较的联合火力打击任务规划评分计算模型,初步实现了任务规划之间的多角度对比分析。
2) 在标准遗传算法的基础上,参考蚁群算法构造,设计了信息素遗传算法,实现了可控性变异,缩短进化收敛代数。
3) 设计了联合火力打击任务规划智能优化的整体流程,通过使用信息素遗传算法实现了任务规划的自动优化,在时间和优化效果上均满足工程实践要求。
4) 信息素遗传算法能够有效解决联合火力打击任务规划问题,具有良好的工程应用效果。
