非广延等离子体中非线性离子声波的数值研究:分数阶模型
2020-09-05赵梅妹
赵梅妹
(西安翻译学院工程技术学院,西安 710105)
1 Introduction
Recently, nonlinear wave structures in electron-positron-ion-dust (EPID) plasma has attracted much attention for several reasons. Such plasma is believed to exist in many astrophysical objects such as active galactic nuclei[1],magnetospheres of pulsar[2],the early universe[3], and the inner regions of the accretion disks surrounding the black hole[4]. The presence of ions could lead to the existence of low frequency waves,i.e.,the ion-acoustic waves (IAWs) which were proposed theoretically by Sagdeev[5]and later confirmed by several observations[6,7]. The positrons have been produced with a large number and long lifetime, which means that they may exist in astrophysical plasmas and laboratory experiments with a high concentration. Also several results[8,9]indicated that the presence of positrons has a considerable influence on the amplitude of IAWs.Since the dust grains (µm to sub-µm sizes) are ubiquitous in the laboratory and space environments such as cometary surroundings, interstellar clouds and planetary rings,they are usually charged due to the absorption of the charged particles. These charged dust grains could either modify the behavior of the normal waves and instabilities, or introduce new eigenmodes. Therefore, four-component EPID plasma could exist in the real world and it is of great interest to study IAWs in EPID plasma[8,9].
In the past few decades, it has been proven that the systems with long-range interaction, fractality of the corresponding time-space, or intrinsic inhomogeneity are intractable within the conventional Boltzmann-Gibbs statistic. The space observations[10,11]and laboratory experiments[12]also indicate the presence of particles which depart from the Maxwellian distribution. Motivated by these findings, a nonextensive generalization of the Boltzmann-Gibbs-Shannon entropy, first recognized by Renyi[13]and subsequently proposed by Tsallis[14], can suitably extend the standard additivity of the entropies to the nonextensive cases. Tsallis distribution can provide a powerful and convenient frame for the analysis of many astrophysical phenomena and present a good fit to the experimental results[15]. What is more important is that the transformation κ=1/(q −1) links q-statistic and κ-distribution[16](for q →1, κ →∞).
In the nature, the next state of a real physical process might depend on not only its current state but also upon its historical states (non-local property, or long-time memory)[17]. To model such systems, the fractional-order derivative is a very natural tool for the description of memory and hereditary properties[18,19]. And it has been shown that new fractional-order models are much more adequate than previously used classical integer-order ones[20],in which such properties are in fact neglected. Therefore,the theory of fractional differential equations has become a hot topic recently due to the exact description of a large number of nonlinear phenomena in fluid flow, physics,chemistry, engineering, finance and other areas of science[21]. Among those fractional derivatives, Jumarie’s modified Riemann-Liouville derivative[22–24]has attracted much attention owing to many interesting properties. For example, the α-order derivative of a constant is zero, and it can be applied to functions which are differentiable or not.
Based on the above findings, the aim of this paper is to investigate the IAWs in a time-fractional EPID plasma whose components are positive ions, negatively charged stationary dust grains, q-nonextensive positrons and electrons. In the basic equations,we change the ordinary integer-order time derivative as Jumarie’s modified Riemann-Liouville fractional derivative, which may have an important physical impact.
2 Basic equations and derivation of KdV equation
Consider a one-dimensional, unmagnetized plasma composed of positive ions, negatively fixed charged immobile dust grains,and q-nonextensive electrons and positrons.In addition, we assume that the phase velocity of the IAWs is much smaller than the electron and positron thermal velocities and larger than the ion thermal velocity, and positron annihilation time is larger than the inverse of the characteristic frequency of the IAWs. The electron-neutrality has the form ni0+np0= ne0+nd0Zd, where ne0,np0,ni0,and nd0are the equilibrium densities of electron,positron,ion,and dust grain,respectively. The nonlinear behavior of IAWs in such EPID plasma may be expressed in terms of normalized variables as

The normalized electron density is given by

while for the positron we have





where Γ(·) is the Gamma function. In the following parts, we shall use at will and for convenience, the notations

for the fractional derivative. Note that changing the integer-order time derivative as a fractional-order one has a considerable physical impact. That is because the integerorder differential equations only consider the instant of time (local property) and the obtained solutions may not confirm the real wave structures in plasmas[25]. This problem can be overcome by introducing the time-fractional derivative in the differential equations. Compared with the conventional ones, the most important advantage of time-fractional differential equations is their non-local property. In (7), the classical integer-order derivative can be recovered if α is an integer.Some useful formulas for Jumarie’s derivative are[22]

Using the above formulas, we can obtain
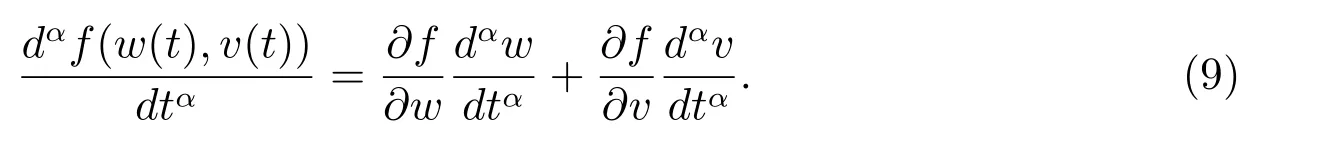
To investigate the nonlinear behavior of small amplitude IAWs propagating in our EPID plasma,we apply the reductive perturbation method to(1)–(5). The independent variables are stretched as

where ϵ is a real small dimensionless expansion parameter and V is the wave group velocity to be determined later.
The dependent variables ni, uiand Φ are expanded as
Substituting (11) into (1)–(5), using the expressions (8) and (9), and collecting all the terms with the same order of ϵ, to the lowest order, we have

From the expression of wave velocity,we can see that IAWs can propagate outward(+)or inward (−). In this paper, we just discuss the outward case.
For the next higher order in ϵ, we have

Using(12),and eliminating n2,u2and Φ2in(13),we can obtain the following KdV equation
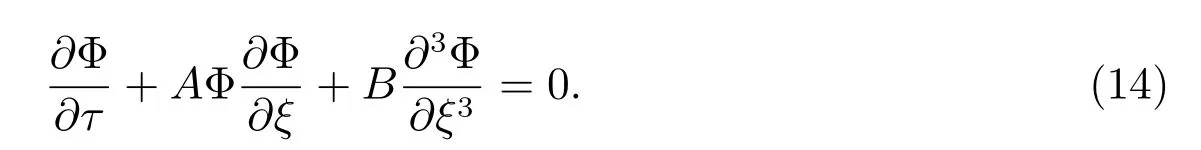
In the above equation, Φ(1)is written as Φ for simplicity, and

3 Numerical analysis and discussions
Although the KdV equation admits some special exact solutions[26], we would expect to have other richer solutions in the practical applications. Hence, the numerical investigation is needed.
Firstly,we will give a brief description of CLG pseudo-spectral method[27]for KdV equation (14) with the following initial and physical boundary conditions



Let Λ=[−1,1], L2(Λ) be the square integrable function space with inner product
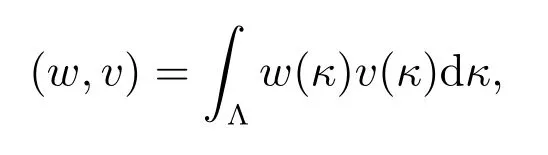
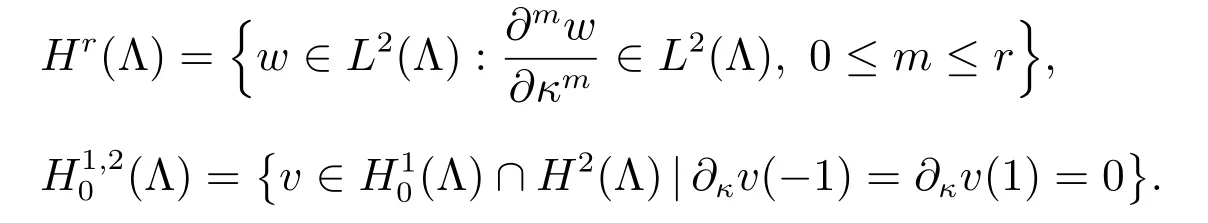
Let
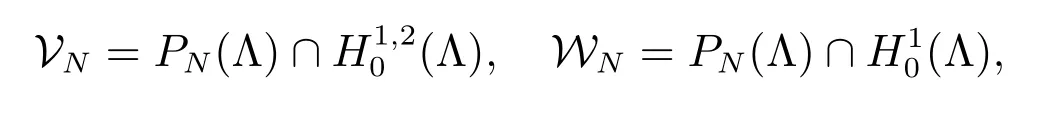
τm=mθ, m=0,1,2,··· , M =τ/θ,
θ be the time step, and Φm=Φ(·,τm). For 0 ≤n ≤N −2, we define
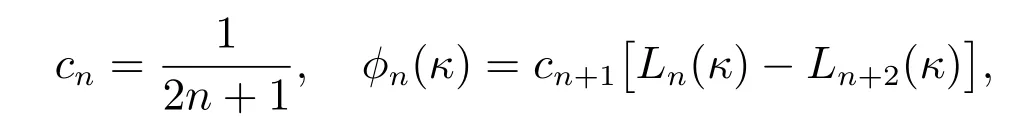

Then we have

The fully-discretization CLG pseudo-spectral method for(17)with conditions(15)and(16) is that: find

such that for all ν(κ)∈WN,

For a better understanding of the ion-acoustic waves, we present the 3D plot for the nonlinear behavior of the waves in Figure 1.

Figure 1: 3D plot for the ion-acoustic waves. The parameters are: α=0.7, q =0.9, µ=0.3, η =0.08, σ =0.2
To see the effects of the fractional derivative parameter α on the solitary IAWs,we present the variation of the soliton profiles for different values of α at τ = 10 in Figure 2. Clearly, the nonlinear structures of IAWs with conditions (15) and (16) are pronouncedly affected by Jumarie’s modified Riemann-Liouville derivative. From plot(a),we can see that when the values of α increase,both the amplitude and width of the compressive soliton increase. The parameter α has the similar effect on the rarefactive soliton, which is shown in plot (b). This interesting phenomenon may be explained as follows: increasing the values of α could enhance the nonlinearity of the EPID plasma,which makes the amplitude of solitary IAWs taller. In other words, the presence of time-nonlocal property (memory property) of the plasma could shrink its nonlinearity and disperse the energy of the system.

Figure 2: Variation of pulse profiles of the solitary IAWs for different values of fractional derivative parameter α. The parameters are: (a) q =0.7, µ=0.7, η =0.01,σ =0.1; (b) q =0.1, µ=0.8, η =0.01, σ =0.2
Figure 3 shows how the nonextensive distribution parameter q influences the solitary IAWs with conditions (15) and (16). It can be seen from plot (a) that both amplitude and width of the compressive soliton increase as the q value increases. Plot(b)shows that increasing q value has the similar qualitative influence on the amplitude and width of the rarefactive soliton. It is revealed that an increase of parameter q will lead to an enhancement of the nonlinearity of the EPID plasma and accumulate a significant amount of energy and therefore the pulses become taller. The parametersµ, η and σ have the same qualitative behavior on the IAWs profiles as Figure 2 and Figure 3, so we do not present these figures here.
4 Conclusions
To summarize, we have investigated the nonlinear structures of solitary IAWs in a time-fractional, nonextensive plasma composed of positive ions, nonextensive electrons and positron, and negatively fixed charged immobile dust grains. In the basic equations, we used Jumarie’s modified Riemann-Liouville fractional derivative to model the time derivative. Using the CLG pseudo-spectral method, we numerically analyzed the effects of the fractional derivative parameter α and nonextensive parameter q on the structures of solitary IAWs. Our results reveal that the time-nonlocal property and nonextensive particle distribution of the EPID plasma play significant roles in changing the profiles of both compressive and rarefactive solitons for the first time. In the practical applications, we can control the energetic pulses in the plasmas by changing the values of these two parameters. The present investigation may provide a better understanding of nonlinear wave phenomena in laboratory plasma experiments and spatial plasmas.
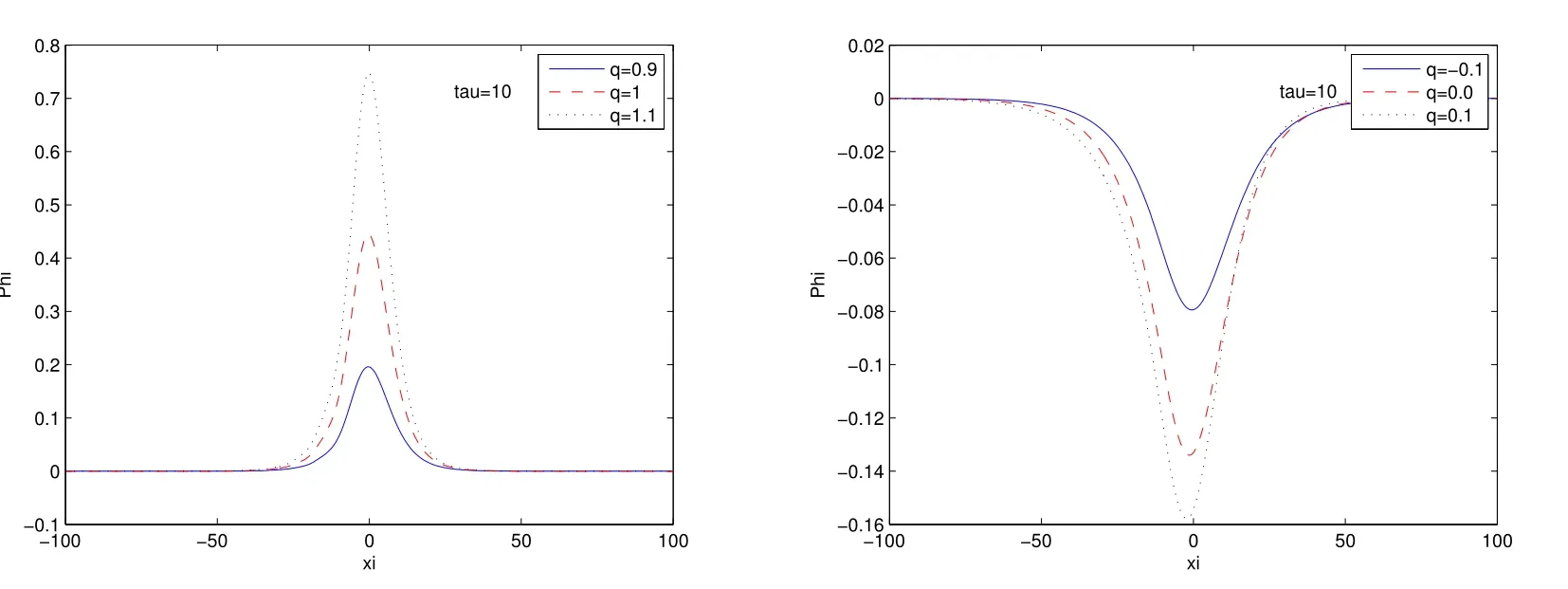
Figure 3: Variation of pulse profiles of the solitary IAWs for different values of nonextensive parameter q. The parameters are: (a) α=0.9, µ=0.6, η =0.02, σ =0.3;(b) α=0.95, µ=0.8, η =0.015, σ =0.5
