含模型不确定性的上三角非线性系统的全局镇定

查雯婷 ，翟军勇，梁营玉

(1.中国矿业大学(北京)机电与信息工程学院，北京 100083;2.东南大学自动化学院，江苏南京 210096)

1 引言

在实际中，由于外部干扰的存在，往往不能建立准确的系统模型，如控制参数未知、非线性函数未知、状态测量函数未知以及系统幂指数未知等.随着控制理论的发展，自适应控制被验证为处理不确定系统强有力的工具.针对系统控制参数未知的情况，文献[1]将反步法与自适应技术相结合，给出了全局状态反馈镇定控制律的设计方法.在某些物理系统中控制方向难以确定，如无标定视觉伺服系统[2].文献[3]利用Nussbaum-type增益方法[4]提出了一种针对三角型不确定非线性系统的重复学习控制策略，然而系统中的非线性函数要求已知.关于未知的非线性函数，通常假设其满足线性增长条件或局部Lipschitz条件.当线性增长率未知时，文献[5]构造了一个通用的自适应输出反馈控制器，使得系统状态调节至原点，该结果被进一步推广至更一般的非线性时滞系统[6-7]和随机系统[8]中.由于传感器测量噪声的存在或者传感器本身的结构特性，系统状态不能被准确测量，从而对控制器的设计带来很大困难.文献[9]基于依次递减齐次度的概念和增加幂积分方法，解决了高阶不确定非线性系统的量测反馈鲁棒控制问题.文献[10]中指出由于外部环境的影响，实际系统模型中的幂指数往往无法确定.通过将未知幂指数漂移量限定在适当范围内，利用区域齐次度的概念构造出一个全局状态反馈镇定控制器.针对幂指数是时变函数的情况，文献[11]利用系统幂指数的上下界设计出一个光滑的状态反馈控制器.

然而，针对模型不确定性的全局控制结果大多集中于下三角系统或严格反馈系统.实际中的物理系统，如球-棍系统和倒立摆系统等，常常被描述成上三角系统或前馈系统.系统结构的特殊性决定了反步法和增加幂积分等方法不再适用于控制器的设计，因此上三角非线性系统的全局控制问题吸引了越来越多控制学者的关注，尤其是高阶上三角非线性系统，即至少一个系统幂指数大于1.嵌套饱和函数方法[12]和forwarding方法[13]是常用的两种控制器设计方法.通过对非线性函数施加适当假设，文献[14]给出了高阶上三角非线性系统的全局镇定饱和控制器设计方法.为了放宽对系统非线性项的约束，文献[15]将嵌套饱和函数和增加幂积分方法相结合，解决了控制参数未知的高阶上三角系统的全局镇定问题.在此基础上，该结果被进一步推广至一类不确定大规模高阶上三角非线性系统中[16].上述嵌套饱和函数方法是基于“由上至下”的原则设计控制器，然后将饱和函数作用于所设计的控制，基于“由下至上”的步骤恰当选取饱和度，使得系统全局镇定.与之不同，基于Lyapunov直接方法的forwarding方法采用的是从下至上的设计思路.文献[17]将扰动观测器与forwarding方法结合，解决了不确定非线性系统的跟踪控制问题.文献[18-19]将forwarding方法与广义齐次度的概念相结合，给出了高阶上三角非线性系统的光滑和非光滑控制器设计方法.在上述已有的结果中，控制器的设计都用到了系统的幂指数.若幂指数未知，该设计方法将不再适用.

为了研究更一般的上三角系统，本文综合考虑系统幂指数、控制参数和非线性函数均不确定的情况，通过将不确定Lyapunov函数与嵌套饱和函数相结合，解决了一类上三角不确定系统的全局镇定问题.本文的难点体现在:1)由于系统幂指数未知，不能利用文献[15]中传统的嵌套饱和函数方法来设计全局镇定控制器;2)文献[10]中针对简单非线性系统的控制器设计方法不适用于本文考虑的上三角结构的系统;3)系统综合考虑各种模型不确定性，给控制器的设计过程带来更多的困难.

2 问题描述及假设

本文研究如下非线性系统的全局镇定问题:

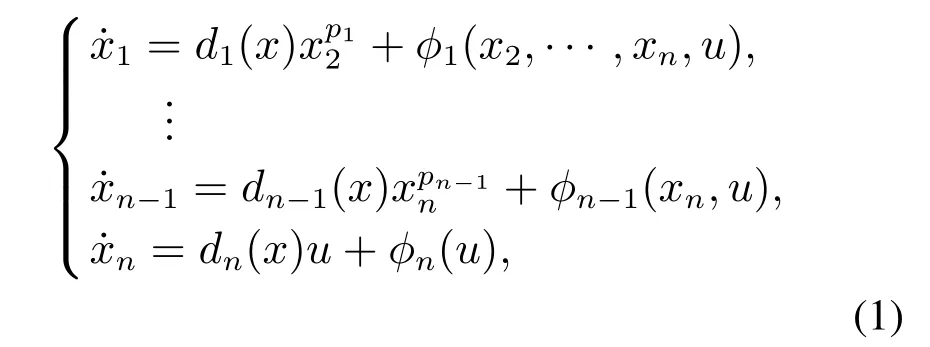
其中:x=(x1··· xn)T∈ℝn，u ∈ℝ分别为系统状态和控制输入.对于i=1，···，n－1，未知幂指数pi，q是两个奇数之比}，并且满足1 ≤ai≤pi≤bi，其中ai和bi均已知.不确定非线性函数di(·)′s和φi(·)′s是C1的，且满足φi(0)=0和di(·)＞0.为了设计一个全局状态反馈控制器，系统(1)需满足如下假设条件:

假设1对于i=1，···，n－2，ai≥bi+1成立.

假设2存在正常数满足

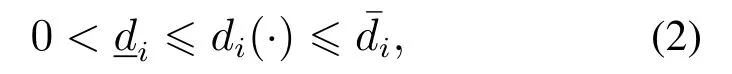
其中:i=1，···，n，xi+1=u.

假设3对于i=1，···，n，存在正常数ρ和qi满足

其中qi＞bi.

注1文献[15]中的假设2.1给出了系统非线性函数所满足的条件，在此基础上设计了齐次饱和控制器来镇定一类更广泛的上三角非线性系统.本文所设计的线性结构控制器是齐次控制器的一种特殊情况，在系统幂指数已知时，上述假设与文献[15]中假设2.1相一致，从而说明了假设的合理性.

下面给出控制器设计过程中会用到两个的引理.

引理1[20]对于任意的，x∈ℝ和y ∈ℝ，以下不等式成立:

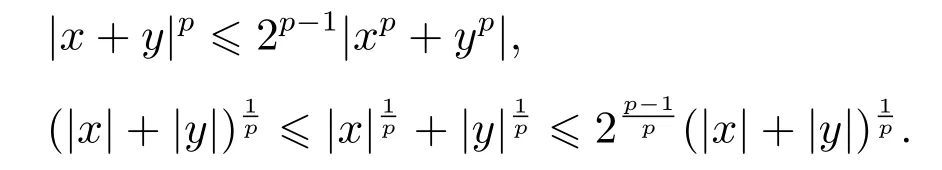
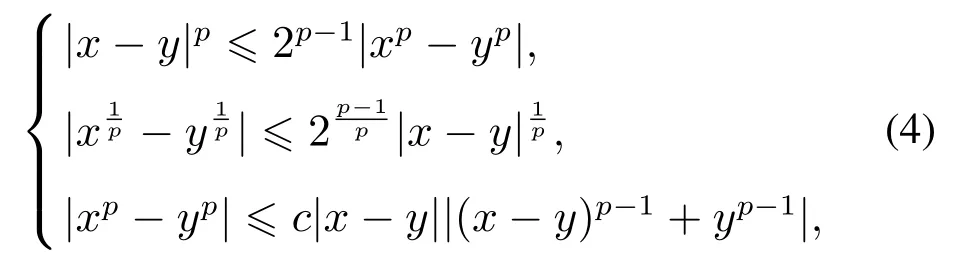
其中c是一个正常数.

引 理2[20]对于任意的正实数c，d 和实函数γ(x，y)＞0，如下不等式成立:

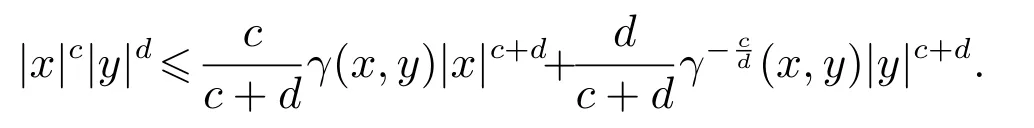
3 局部镇定控制器设计

本节针对系统(1)设计状态反馈控制器，使得闭环系统达到局部稳定.首先，考虑如下标称系统:

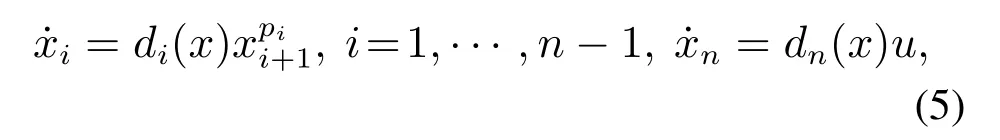
并基于Lyapunov理论[21]迭代地设计局部状态反馈控制器.

步骤1选取Lyapunov函数，可得V1关于时间的导数为

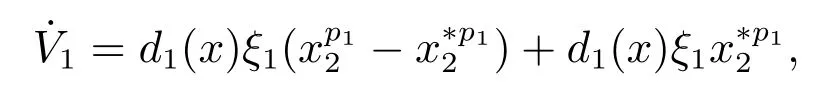
针对Lyapunov函数V1，定义集合

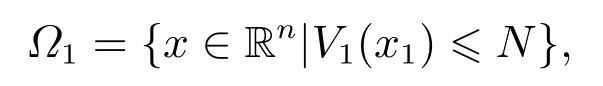
其中N是一个正常数.通过设计线性虚拟控制器

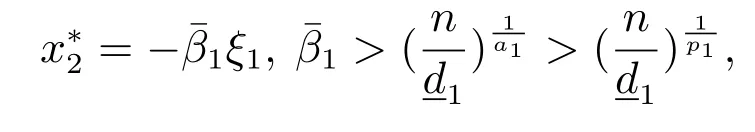
可得

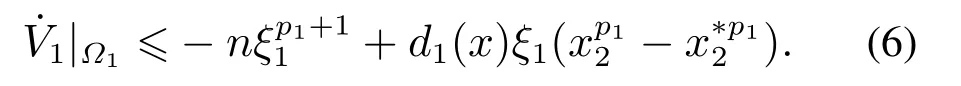
步骤k假设在第k－1步，存在一个关于x1，···，xk-1正定且径向无界的Lyapunov函数Vk-1:ℝk-1→ℝ和一系列虚拟控制器，

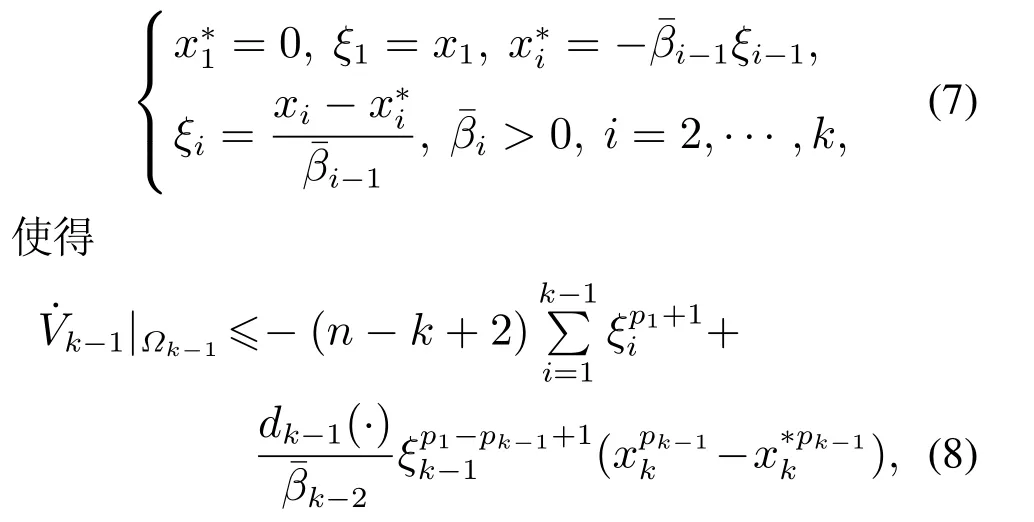
其中定义集合Ωj≜{x ∈ℝn|Vj(x1，···，xj)≤N}，j=2，···，k－1满足Ωk-1⊂···⊂Ω1.

接下来证明式(8)在第k步仍然成立.为了简便，利用一个通用的常数c来表示任意有限的正常数，且具体的数值随着位置的不同而改变.选取如下Lyapunov函数:

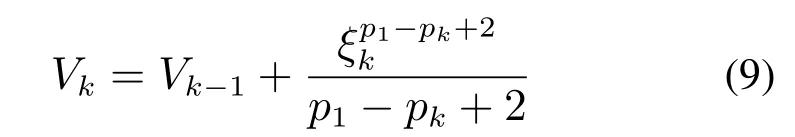
和相应的集合Ωk={x ∈ℝn|Vk(x1，···，xk)≤N}.由定义可知，Ωk⊂Ωk-1成立.

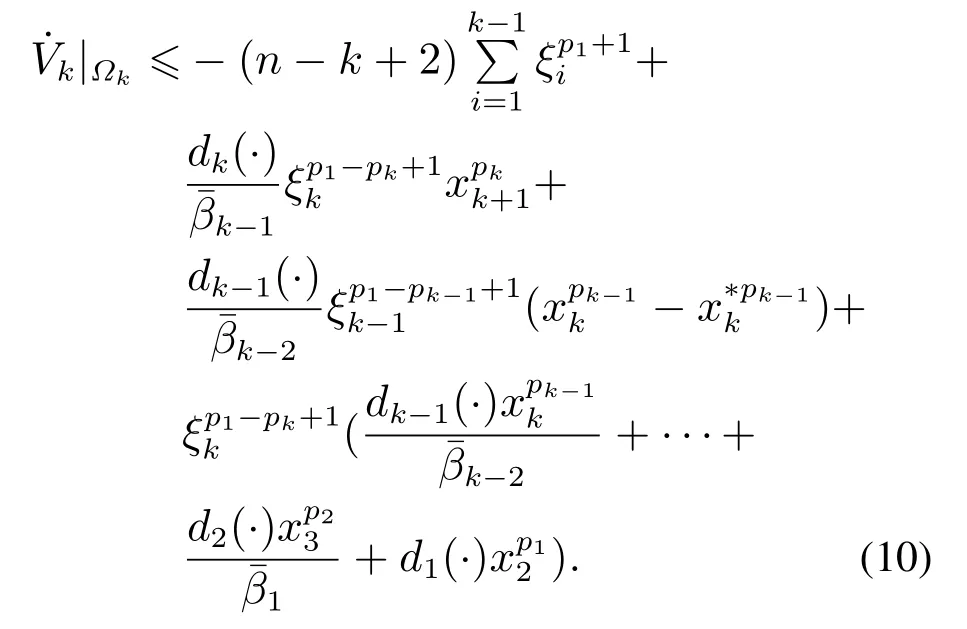
根据ξk的定义，由引理1-2可得

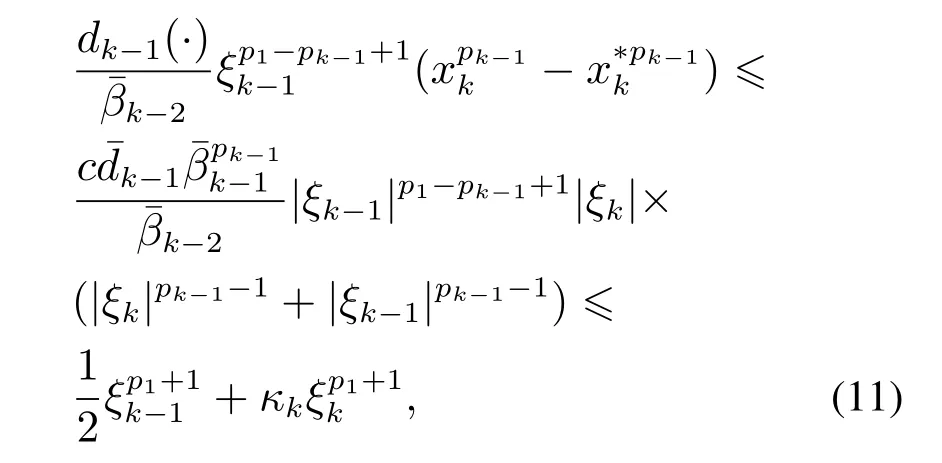
其中κk是与ai和bi有关的正常数，i=1，···，k－1.

由假设1可知，p1≥···≥pk成立.因此，根据引理1-2可得

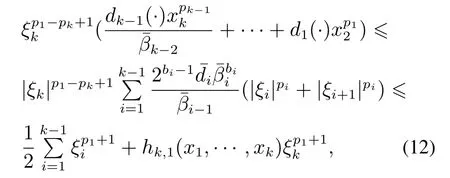
其中hk，1(·)≥0是一个只和上下界有关的连续函数，.

将式(11)-(12)代入式(10)中，可得

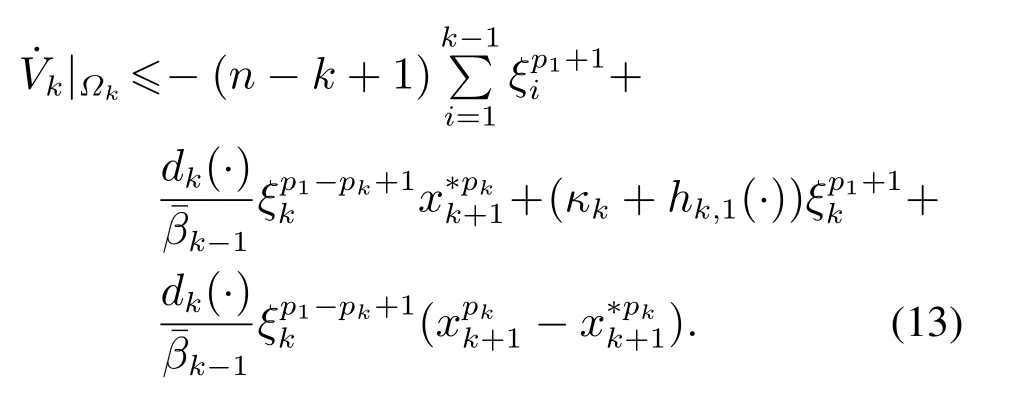
由p1≥···≥pk知，Vk是一个关于x1，···，xk正定且径向无界的函数，从而x1，···，xk在Ωk上有界.由于hk，1(·)关于x1，···，xk连续，则hk，1(·)在Ωk上有界，即是一个常数.

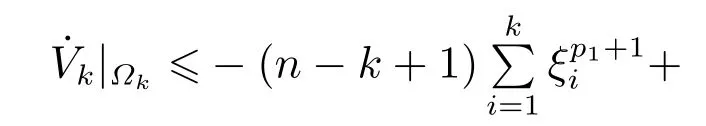
归纳部分证明完毕.

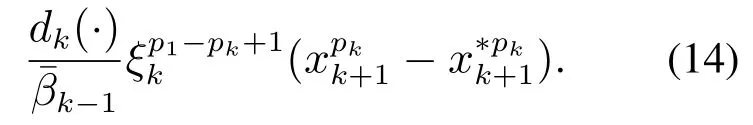
步骤n根据数学归纳法可知，式(14)在k=n时仍然成立.故存在一个线性控制器

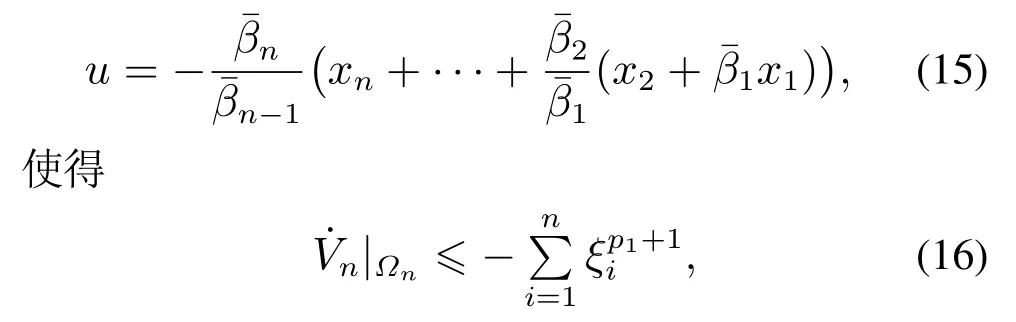
其中:Lyapunov函数

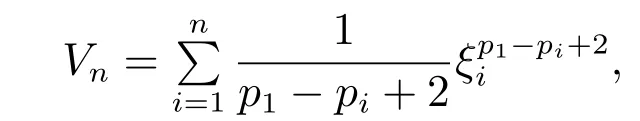
集合Ωn≜{x ∈ℝn|Vn(x1，···，xn)≤N}满足Ωn⊂···⊂Ω1.因此，由Lyapunov稳定性定理可知闭环系统(5)-(15)在集合Ωn上是局部渐近稳定的.

综合考虑系统(1)和标称系统(5)的关系，可得在控制器(15)作用下，Lyapunov函数Vn关于系统(1)的导数为

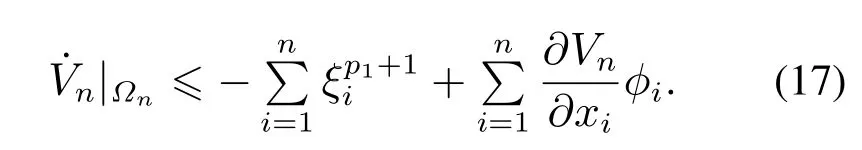
由假设1-3可知qi＞pi≥pi+1≥···≥pn，则不等式(17)中的非线性项可估计为

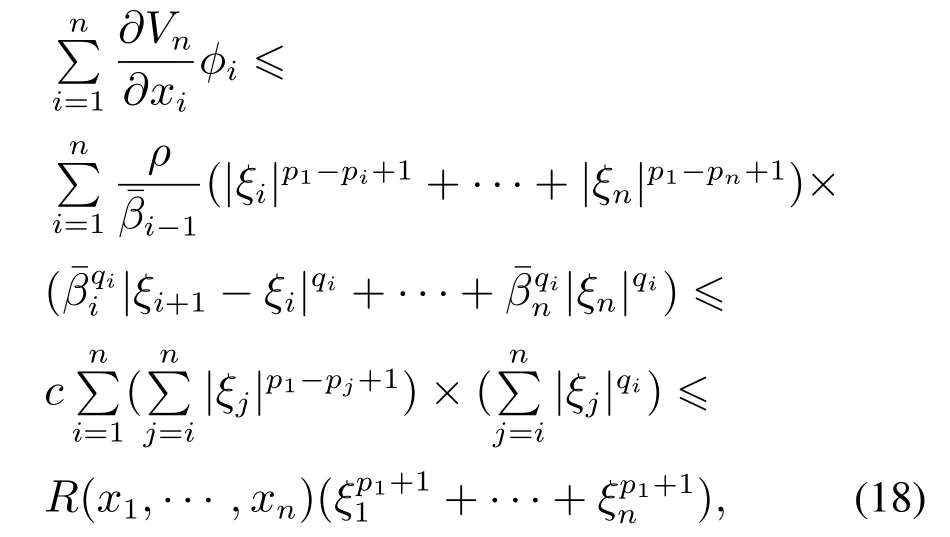
其中R(·)≥0是关于x1，···，xn的连续函数.

由于Lyapunov函数Vn关于x1，···，xn是正定且径向无界的，因此通过恰当选取N，使得∀x ∈Ωn，R(·)成立.结合式(17)可知

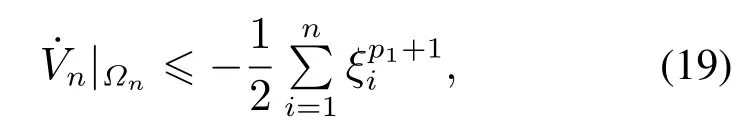
进而可得闭环系统(1)-(15)在集合Ωn上是局部渐近稳定的.

4 全局饱和控制器设计

本节将进一步考虑非线性系统(1)的全局渐近镇定问题.将设计的控制器(15)与饱和函数

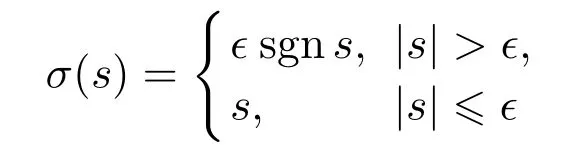
相结合，得到如下饱和控制器:

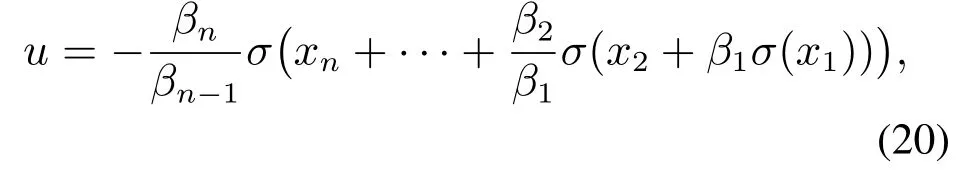
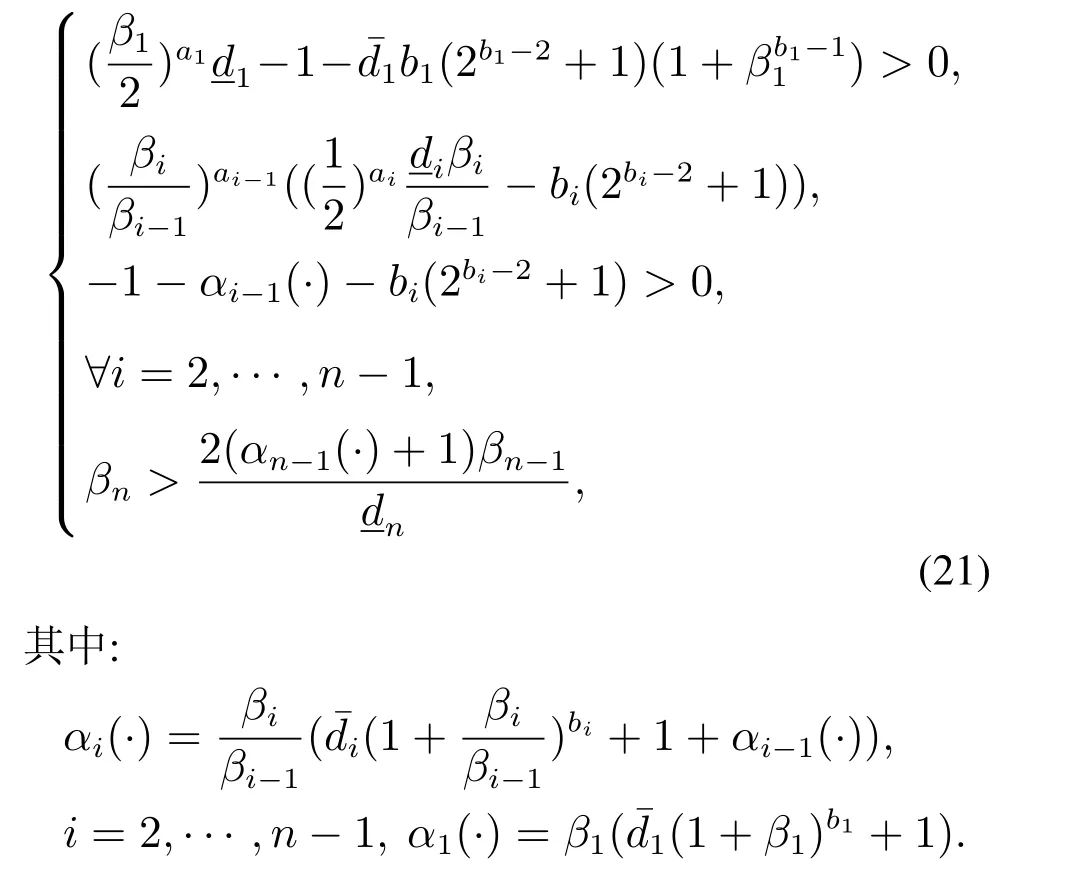
首先引入下列引理，该引理的证明将在附录中给出.

引理3对于闭环系统(1)-(20)，若系统状态满足，j=i+1，···，n，则存在式(21)中定义的αi(β1，···，βi)和0 ＜ϵ1＜1，使得对于任意的0 ＜ϵ ≤ϵ1，如下不等式成立:∀i=1，···，n，

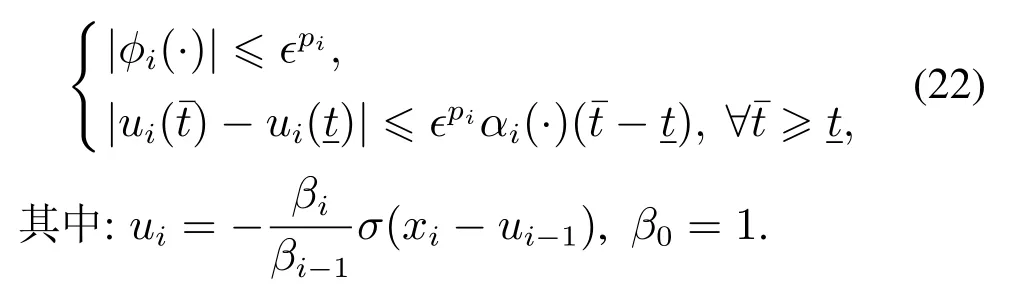
在引理3的基础上，如下定理给出了本文的主要结论.

定理1在假设1-3的条件下，存在充分小的ϵ ∈(0，ϵ1]，使得饱和控制器(20)能够全局镇定非线性系统(1).

证上一节给出了系统(1)在集合Ωn中局部镇定的结论.如果能够证明在饱和控制器(20)作用下，系统状态经过一段时间后能够进入并永远停留在集合Ωn中，则系统(1)全局稳定的结论自然成立.因此，该定理的证明分为如下两步:

首先，利用归纳法证明当βi满足式(21)时，饱和控制器(20)能够使得系统状态依次收敛到一个由ϵ决定的小区域内.

步骤1证明存在时刻t1＞0，使得∀t ≥t1，

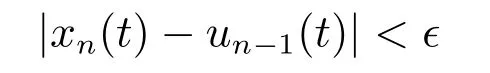
成立.为了得到这个结论，首先利用反证法证明存在时刻t1＞0，使得

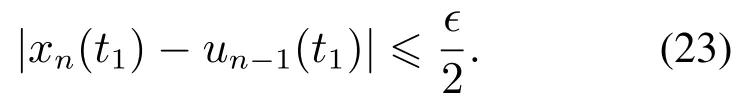
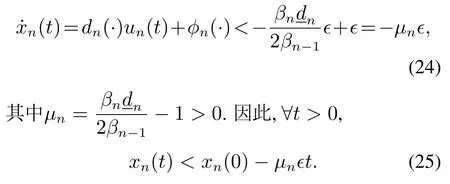
由un-1的定义可知，从而∀t ＞0，

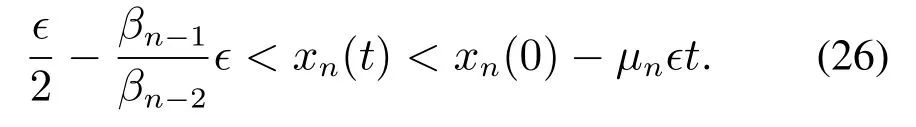
当时间趋近于无穷大时，上式中的xn(0)－μnϵt将会趋近于负无穷大，式(26)导致矛盾.从而，

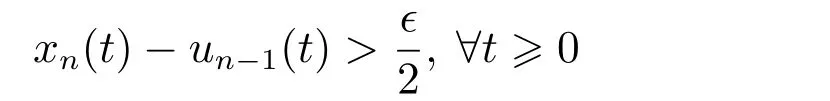
不成立.类似可得负的情形也不成立，因此∃t1＞0，使得式(23)成立.

接下来同样利用反证法证明∀t ≥t1，

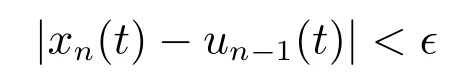
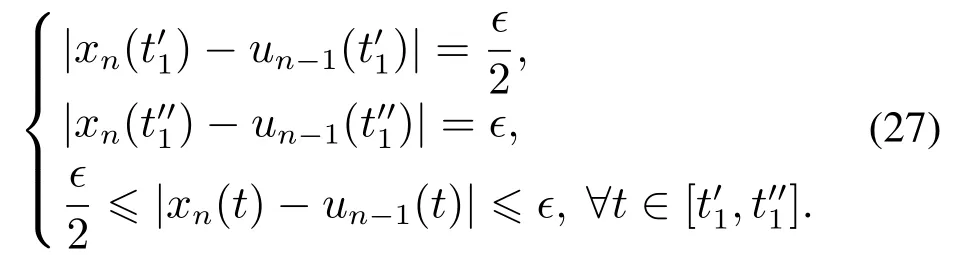
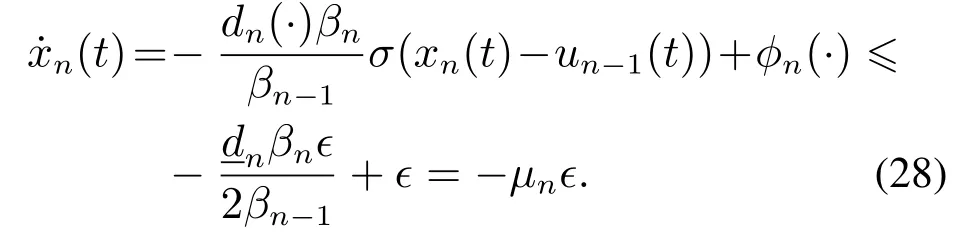
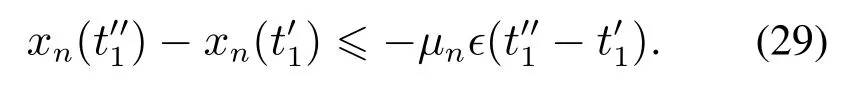
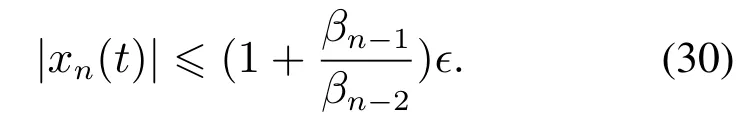
从而由引理3可知

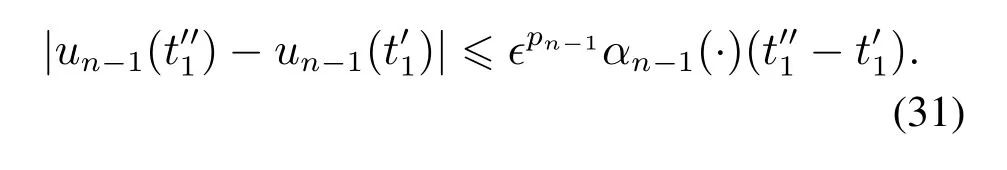
结合式(29)-(31)可知

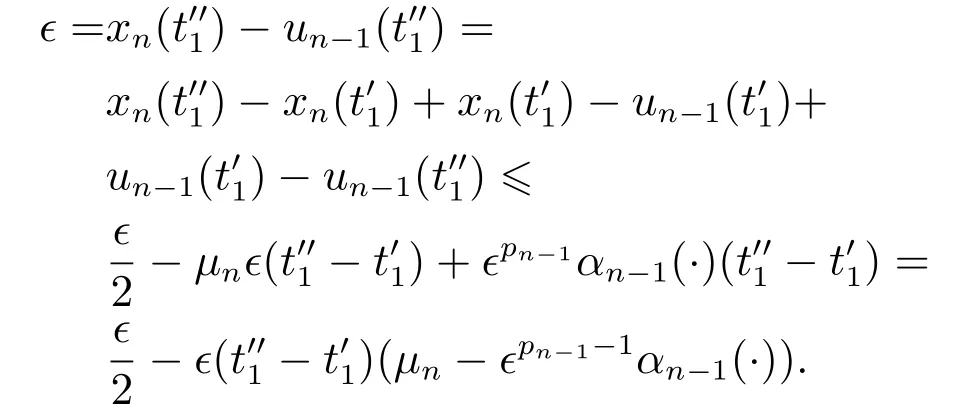
根据式(21)中βn可得μn－ϵpn-1-1αn-1(·)＞0，从而矛盾.因此，式(27)中正的情形不成立.利用类似的方法可以证明，式(27)中负的情形也不成立.故存在一个时刻t1＞0，对于任意的t ≥t1，有|xn(t)－un-1(t)|＜ϵ，即

Xn(t)∈Qn={Xn(t):|xn(t)－un-1(t)|＜ϵ}.

步骤i假设存在时刻0 ≤t1≤···≤ti-1，使得∀t ≥ti-1，有

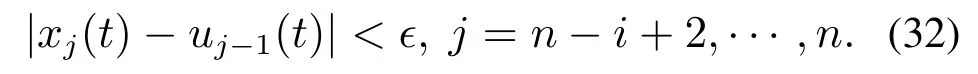
现要证明上式在j=n－i+1时仍成立.按照步骤1中的证明过程，首先证明∃ti≥ti-1，使得

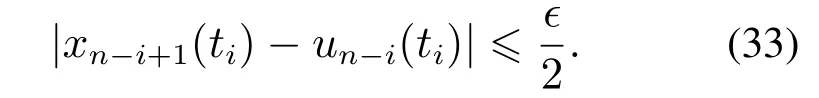
利用反证法，假设上式不成立，则∀t ≥ti-1有

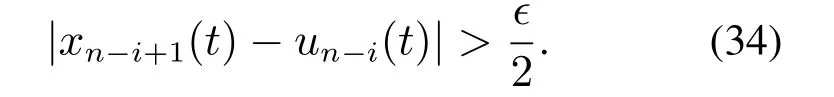
为了证明的完整性，这里考虑式(33)中负的情况，即

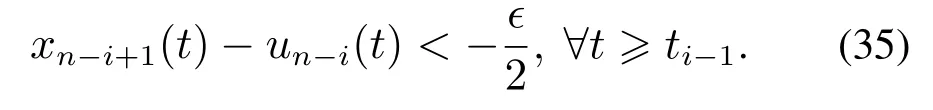
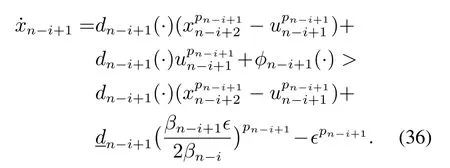
根据引理1，给出如下估计:

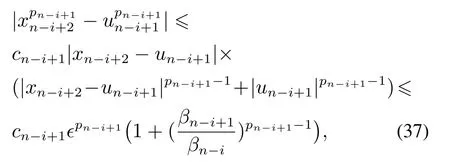
其中cn-i+1=bn-i+1(2bn-i+1-2+1).

将式(37)代入式(36)中，可知∀t ≥ti-1，

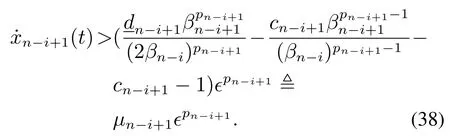
根据式(21)中βi's的取值可知μn-i+1＞0.因此，由式(38)可得∀t ≥ti-1，

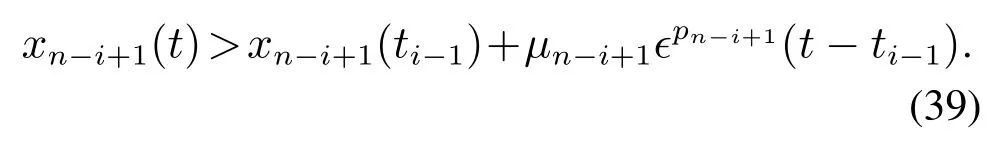
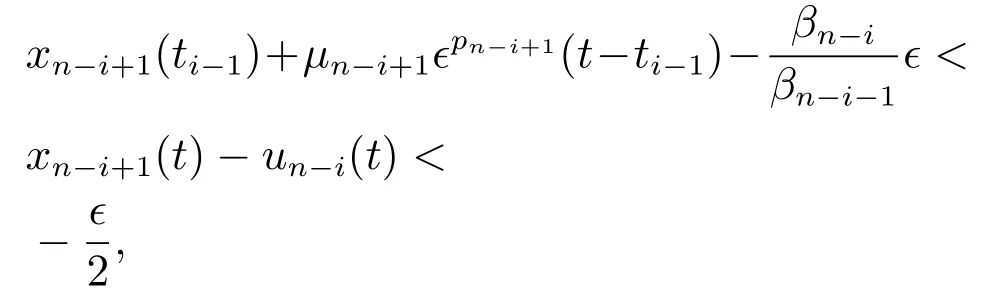
其中∀t ≥ti-1.类似于式(26)，当时间t趋近于无穷大时，上述不等式变成，矛盾.因此，式(35)不成立.对于正的情形，可参照第1步的证明过程.故必然存在时刻ti使得式(33)成立.

接下来，同样利用反证法证明∀t ≥ti，有

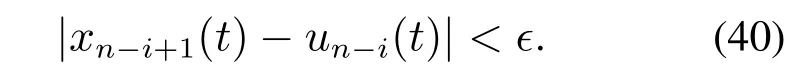
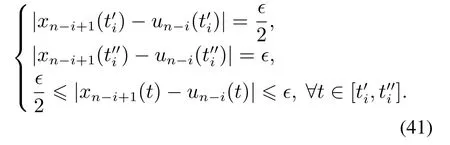
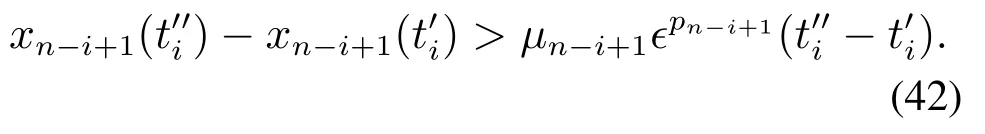
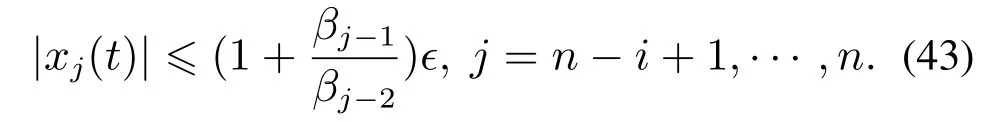
因此，根据引理3得

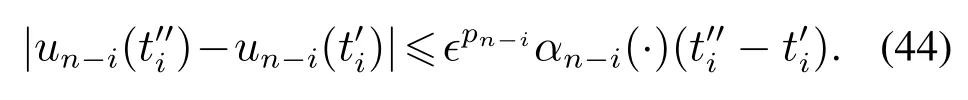
结合式(41)-(42)以及式(44)，可知

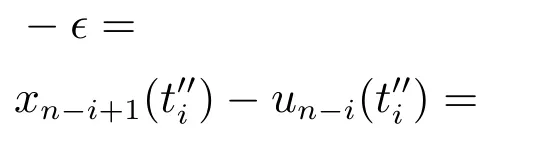
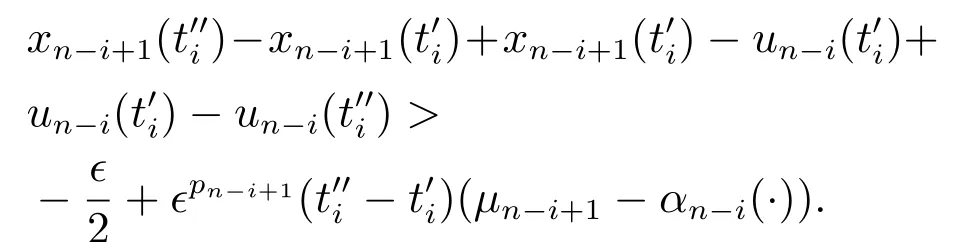
由式(21)中βi's的取值可得μn-i+1－αn-i(·)＞0，从而矛盾.故式(41)中负的情形不成立，同理可证明正的情形不成立.

综上可知，存在一个时刻ti≥ti-1，使得∀t ≥ti，|xj(t)－uj-1(t)|≤ϵ成立，j=n－i+1，···，n.

步骤n根据上述证明过程，由数学归纳法可知，存在时刻tn-1≥···≥t1≥0，使得∀t ≥tn-1，

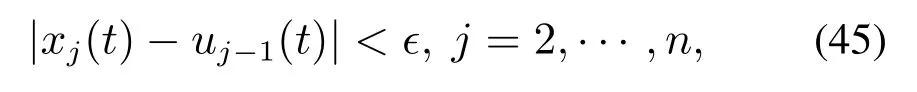
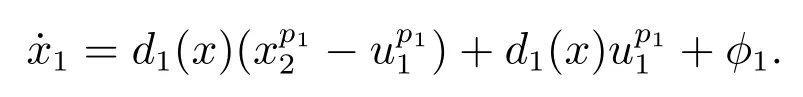
由引理3可知|φ1(·)|≤ϵp1，∀t≥tn-1.此外，由引理1-2可得

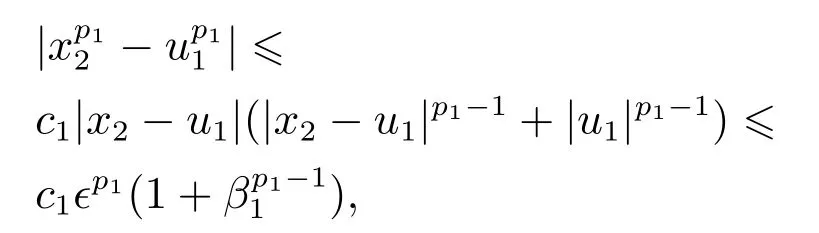
其中c1=b1(2b1-2+1).

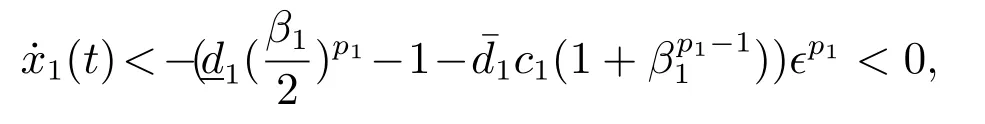
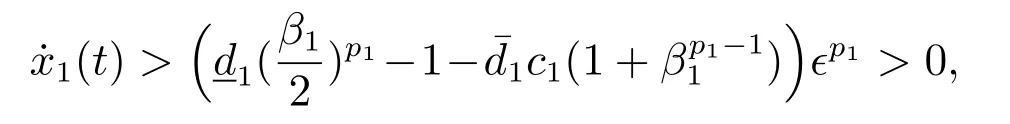
则对于任意的t ≥tn-1，系统状态x1不可能恒小于.

综合上述两种情况可知，存在一个时刻tn≥tn-1使得当∀t ≥tn时，.因此，在时刻tn之后，系统状态Xn(t)将会进入并一直停留在区域Q中，

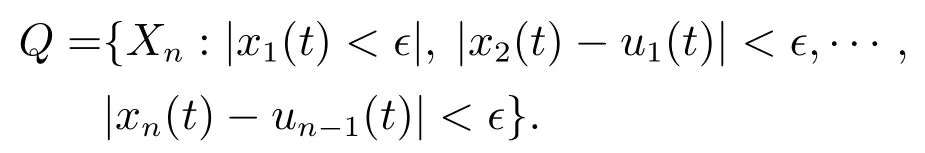
从Q的定义可知，区域Q的大小由饱和度ϵ决定.此外，由第2节可知闭环系统(5)-(15)在区域Ωn上局部渐近稳定.故通过恰当选取参数ϵ满足集合Q⊂Ωn，可得在tn时间之后，系统状态停留在集合Q中，并且饱和控制器(20)将退变成非饱和控制器(15).同时，在控制器(15)作用下，系统状态渐近收敛到原点.因此，闭环系统(5)-(20)是全局渐近稳定的. 证毕.

5 数值仿真

本节将利用一个数值仿真例子来验证定理1中所设计控制算法的有效性.

例1考虑如下非线性系统:

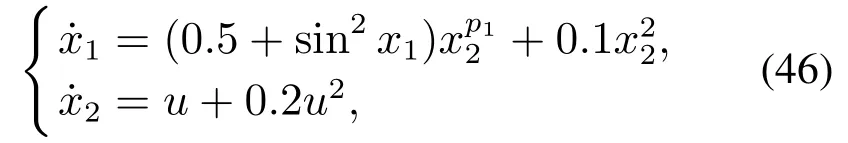
其中p1是未知的幂指数并且满足p1∈[1，2].通过计算可知，0 ＜0.5 ≤0.5+sin2x1≤1.5，从而满足假设2.同理可验证假设1和假设3均成立.因此根据定理1，利用未知幂指数p1的上下界可以设计出如下线性饱和控制器

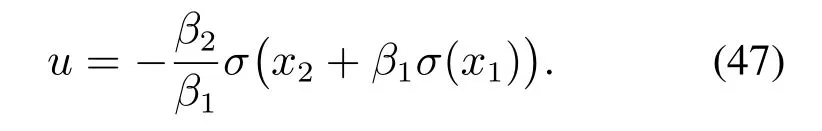
取β1=2，β2=12，，饱和函数的饱和度ϵ=0.2.初始状态为(x1(0)，x2(0))=(0.5，－0.5).状态响应曲线和控制曲线仿真结果如图1-2所示.

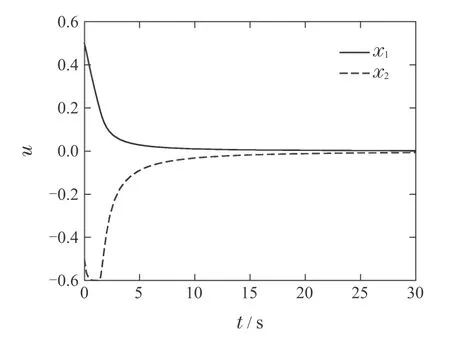
图1 p1=时闭环系统(46)-(47)的状态响应曲线Fig.1 State trajectories of the closed-loop systems (46)-(47)with p1=

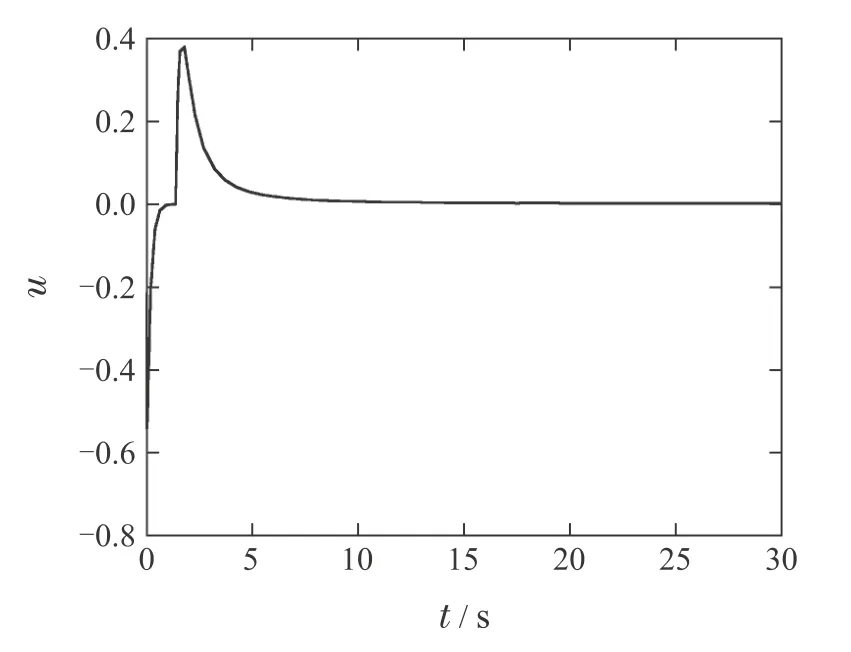
图2 p1=时闭环系统(46)-(47)的控制曲线Fig.2 Control trajectory of the closed-loop systems(46)-(47)with p1=

此外，从控制器设计过程中可知，只要幂指数p1在[1，2]中取值，所设计的控制器u均可全局镇定系统(46).为了验证控制器的鲁棒性，选取得到如图3-4所示的仿真结果.在同样的控制器(47)作用下，系统状态渐近收敛至原点，这与理论分析的结果相一致.

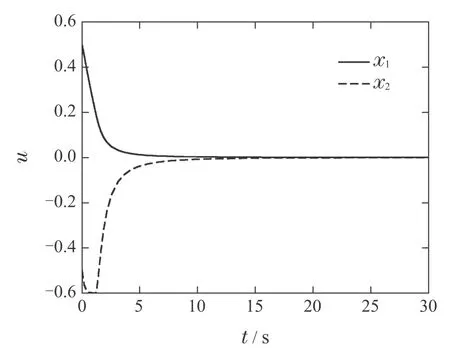
图3 p1=时闭环系统(46)-(47)的状态响应曲线Fig.3 State trajectories of the closed-loop systems (46)-(47)with p1=

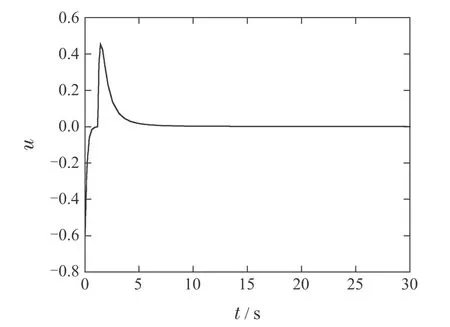
图4 p1=时闭环系统(46)-(47)的控制曲线Fig.4 Control trajectory of the closed-loop systems(46)-(47)with p1=

6 结论

本文基于Lyapunov稳定性理论，给出了一种嵌套饱和控制器的设计方法.只要系统不确定性能够限定在指定范围内，该控制器能够全局镇定一类上三角非线性系统.与现有结果对比，本文的创新点体现在:1)考虑由于建模不确定性引发的系统幂指数未知的情况，只利用已知的上下界设计出全局镇定控制器，同时具有一定的鲁棒性;2)除此之外，系统中含有更多的不确定非线性函数，从而能够涵盖一类更广的非线性系统;3)与已有的齐次控制器[15]相比，设计的线性控制器具有更简单的结构，便于在实际工程中的应用.

附录 引理3的证明