不确定通信拓扑下多智能体系统鲁棒一致性
2020-09-05陈阳舟黄小龙詹璟原
陈阳舟,黄小龙,詹璟原
(北京工业大学人工智能与自动化学院,北京 100124)
1 引言
近年来,多智能体系统一致性问题研究受到了国内外学者的广泛关注,主要原因在于其广泛的应用前景,譬如各类运动体的编队控制、群集运动、蜂拥控制以及分布式传感器网络融合的应用等[1].解决一致性问题的关键在于设计合适的控制协议,使得各智能体通过网络通信获取邻居信息,并依此来调整自身的状态,从而使各自状态渐近地或有限时间内达到一致.尽管多智能体系统一致性理论研究取得了很大的进展,但还存在一些不足.例如针对系统中各种不确定性情况(包括模型不确定性和通信不确定性等)的鲁棒一致性问题研究还不充分.本文重点考虑一般确定性线性多智能体系统在不确定通信权值下的鲁棒一致性问题.
实际系统中,由于智能体之间的通信连接不可靠或受通讯范围限制,智能体之间的信息拓扑可能会动态变化.针对此类问题,一种方法是将通信拓扑考虑为马尔可夫切换过程.例如,文献[2]研究了线性多智能体系统基于马尔可夫切换通信拓扑的一致性条件.文献[3]研究了具有网络拓扑随机时延的二阶离散多智能体系统的一致性.文献[4]分别考虑了二阶多智能体系统在具有与不具有时延两种情况下的一致性条件.文献[5]利用Lyapunov方法,证明了在随机网络切换拓扑下,连续与离散多智能体系统实现均方一致的条件.
另一种针对具有不确定性通信拓扑的多智能体系统的研究方法是基于鲁棒控制理论.文献[6-7]采用矩阵不等式方法分析具有不确定性通信拓扑的单积分多智能体系统一致性问题,提出了实现平均一致性的充分条件.文献[8]研究具有不确定性通信拓扑的二阶线性多智能体系统鲁棒H∞一致性控制问题,提出了实现鲁棒H∞平均一致性控制的充分条件.文献[9]研究具有不确定性通信拓扑的一阶线性多智能体系统鲁棒H∞一致性控制问题,通过构造跟踪虚拟领导者,实现了当系统稳定时的鲁棒H∞一致性控制.文献[10]研究具有外界干扰的三阶线性多智能体系统鲁棒H∞一致性控制问题,设计控制协议满足在不确定拓扑和状态时滞的情况下,实现鲁棒H∞一致性控制.文献[11]研究了网络拓扑同时存在通信时延和结构不确定的多智能体系统一致性问题.采用图论方法将一致性问题转化为系统的渐近稳定性问题.文献[12]针对存在不确定性通信拓扑多智能体系统,采用线性分式变换方法,解决鲁棒一致性问题.文献[13]针对存在不确定性通信拓扑和外界干扰的二阶线性多智能体系统,采取鲁棒H∞控制,实现了鲁棒H∞旋转平均一致性.文献[14]针对多智能体不确定性和网络不确定性,根据第一个智能体状态变量与其他智能体状态变量之差,列出新的状态方程,设计控制协议,实现了多智能体系统鲁棒H∞一致性问题.文献[15]研究具有网络的不确定性二阶线性多智能体系统,将不确定拓扑参数重新定义为自变量,将多智能体系统构造为一个特殊的多项式系统,利用控制系统的稳定性理论将鲁棒一致性问题转化为误差模型的鲁棒稳定性分析.文献[16-17]针对存在外部干扰的离散时间多智能体系统,在无向不确定性拓扑情况下,推导出鲁棒H∞平均一致性控制的充分条件.
上述研究存在一些不足之处:一是考虑的模型可能为一阶或二阶的特殊情况;二是限定为平均一致性,即群体决策量为所有个体初始状态的平均值,这通常要求网络拓扑是无向图或者是平衡的有向图[18].本文在现有研究基础上,针对一般高阶线性多智能体系统和一般有向通信拓扑,提出一种基于线性变换的鲁棒部分变元渐近稳定性方法解决通信不确定性情况下的多智能体系统状态一致性问题.首先,选取标称通信拓扑图G的有向生成树的关联矩阵构造线性变换,采用该变换将多智能体系统状态一致性问题转化为相应线性系统的鲁棒部分变元渐近稳定性问题.其次,通过对拉普拉斯摄动矩阵ΔL进行分解,使其满足不确定性匹配条件,从而将一致性协议的增益矩阵求解转化为参数不确定系统的鲁棒二次镇定问题.最后,应用鲁棒二次稳定性与镇定控制方法给出一致性条件和协议增益矩阵设计过程.通过数值仿真例子验证本文提出方法的正确性和有效性.
本文采用diag{·}表示对角矩阵;|·|表示绝对值;‖·‖表示欧式范数.
2 问题描述
考虑N个连续时间线性智能体组成的多智能体系统,其中第i个智能体的状态方程为
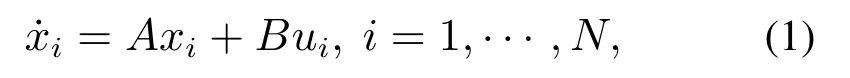
这里xi∈ℝn和ui∈ℝp分别表示第i个智能体的状态和控制(或称为协议).
假设智能体之间的通信关系由有向图G=(V,E)表示,其中V={1,···,N}表示智能体编号集合,E={(i,j):i,j ∈V}表示智能体间的通信连接关系,即边(j,i)∈E表示智能体j可传递信息给智能体i(此时称智能体j为智能体i的通信邻居).定义智能体i的通信邻居集合Ni={j :(j,i)∈E,j ∈V,i/=j},由此智能体之间的通信关系可以用智能体通信邻居集合{Ni:i=1,···,N}表示.进一步,假设智能体间的通信连接强度具有不确定性,即有向图G的有向边(j,i)的权值表示为aij+Δaij≥0,其中aij>0为标称连接权值,Δaij为未知有界权值,表示通信连接的不确定性.假设存在标量ρij≥0使得|Δaij|≤ρij.
本文目的是针对具有不确定性通信连接的多智能体系统(1),设计控制协议ui使得其在该控制协议下达到状态一致.
假设基于智能体i与其邻居智能体j ∈Ni之间的局部状态信息,构造如下分布式控制协议:

其中K ∈ℝp×n为需要设计的反馈增益矩阵.
定义1对于智能体i任意的初始状态xi(0)和任意满足|Δaij|≤ρij的有界不确定性通信连接,如果智能体(1)在协议(2)作用下满足
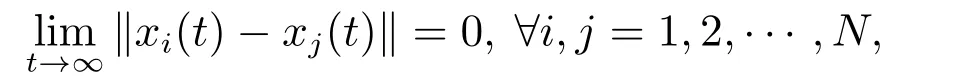
则称系统(1)达到通信连接鲁棒状态一致.
定义2一个有向图称为一棵树,如果除根节点以外的其他所有节点都只有一个父节点;一个有向图称为包含一棵有向生成树,如果存在一棵包含该有向图所有节点的树[19-20].
本文假定通信图在标称连接权值条件下存在有向生成树.
3 基于线性变换的一致性问题转化
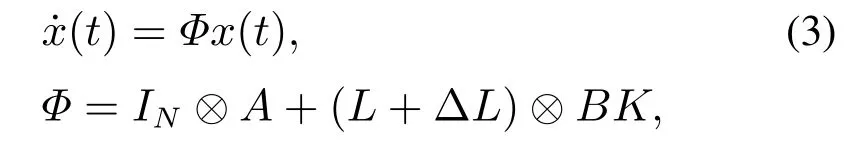
其中:L为有向图G相应于权值aij的拉普拉斯矩阵,ΔL=[Δlij]N×N表示为对应于不确定性Δaij的拉普拉斯矩阵,其中

注意这里容许摄动Δaij为负值,且使得aij+Δaij≥0.
与文献[9-10]不同,本文假设每个有向边权值摄动互相独立,这更符合实际情况.下面对摄动矩阵ΔL进行分解,使其满足如下匹配条件ΔL=EΣ(t)F,其中:E和F为具有适当维数的已知矩阵;Σ(t)为未知函数矩阵,属于满足如下范数有界条件的集合:
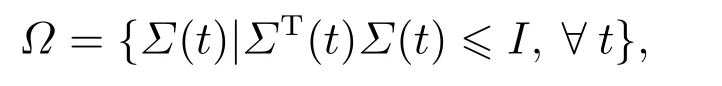
分解过程依赖于如下引理1:
引理1[8]给定顶点数为N边数为M的有向图G,定义矩阵和D=[dpj]M×N如下:

让Σ(t)=diag{q1,···,qM},其中qp=Δap/ρp表示第p条边的归一化摄动权值,则有向图G的不确定拉普拉斯矩阵ΔL可以表示为

其中:F=ρδ(ET-D),ρδ=diag{ρij}.
选取图G在标称连接权值条件下的有向生成树的关联矩阵来构造线性变换,将具有不确定性通信拓扑的多智能体系统的一致性问题等价地转换为相应线性系统的鲁棒部分变元渐近稳定性问题.
有向图G的有向生成树包含N个节点和N-1条有向边.设该有向生成树的N ×(N-1)关联矩阵为,其行对应生成树的节点,列对应生成树的有向边,第i行第j列的元素wij定义为


其中:1N表示元素全为1的N维列向量,In表示n×n维单位矩阵,Wi∈ℝn×(Nn),相应的逆矩阵W-1可以表示为

利用矩阵(5)构造系统(3)的线性变换

将其可转化为如下形式的不确定系统:
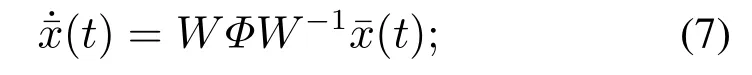
或如下结构分解的形式:

引理2不确定系统(7)具有下面的形式:
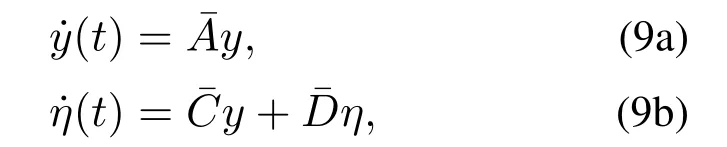
证根据线性变换矩阵W和拉普拉斯矩阵的性质,可得如下3个条件:
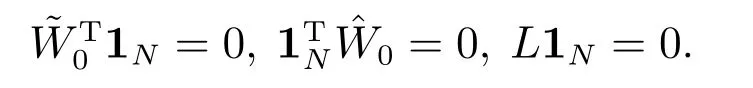
另外ΔL的第i个对角元素等于所有以节点i为终端节点的边的摄动权值之和,所以ΔL1N=0依然成立.结合矩阵的Kronecker积的性质,可得到不确定系统(8)的系数矩阵分别为
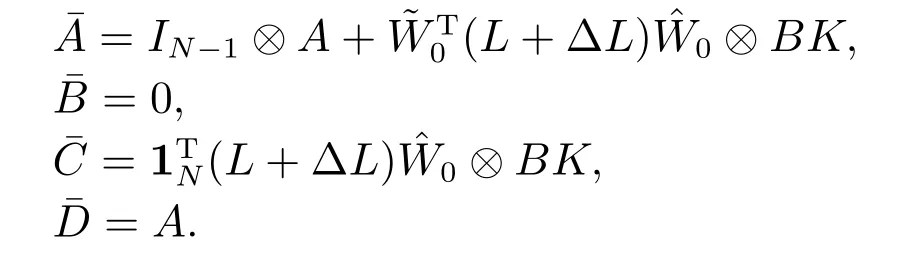
因此系统(7)具有系统(9)的形式. 证毕.
由此可知,y=0 ⇔x1=x2=···=xN,即多智能体系统(1)的渐近鲁棒一致等价于(9)的部分变元y鲁棒渐近稳定.等价地,多智能体系统(1)的渐近鲁棒一致当且仅当鲁棒渐近稳定.
注1本文通过线性变换(6)将多智能体一致性问题转化为部分变元y渐近稳定性问题,然后通过线性变换后的系统稳定性条件求解控制协议参数,使多智能体系统能够在所设计的控制协议下达到渐近稳定一致.平均误差变量构建的变换矩阵方法要求网络拓扑是无向图或者是平衡的有向图,而本文构建关联矩阵的线性变换方法对网络拓扑无上述特殊要求,适用于包含有向生成树的有向图情形,因此更具一般性.本文方法优势还在于控制算法易于实现,针对性能可分析的降阶子系统,设计该系统的稳定化控制律,实现(N -1)n维变量y稳定,就可以确定多智能体系统所有节点的状态最终趋于一致.
注2线性变换(6)中的矩阵是基于标称通信拓扑图的有向生成树的关联矩阵构造的,这个有向生成树可能由于连接权值摄动而被破坏,即使连接权值摄动后的通信图不再具有该生成树,但这并不影响笔者采用基于该生成树的变换矩阵.事实上,如文献[19-20]一样,可以不考虑这个变换矩阵与通信拓扑图的权值摄动有关联性.
4 多智能体系统一致条件和协议设计
为便于分析不确定性系统(9a)的鲁棒渐近稳定性,首先介绍如下两个引理.
引理3[21]对于适当维数的已知矩阵Ψ=ΨT,E,F和满足ΣT(t)Σ(t)≤I的未知Σ(t),不等式

成立的充分必要条件是:存在标量ε >0使得

引理4[21]将对称矩阵S分割为
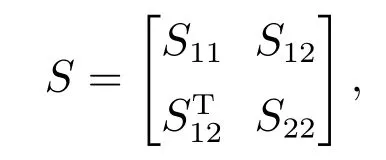
其中:S11∈ℝr×r,S12∈ℝr×(n-r),S22∈ℝ(n-r)×(n-r),则S <0当且仅当以下条件之一成立:
10年前,我曾来过这个博物馆。这次再来,最大的感受,就是鲁迅还活着,活在跳动的文字里,活在人们的心目中。

定义3对于具有参数不确定性的系统(9a),如果存在一个正定矩阵IN-1⊗P(即P为正定矩阵)和一个正的标量α,使得对任意的不确定性(4),Lyapunov函数V(y)=yT(IN-1⊗P)y沿着系统(9a)的状态轨迹关于时间的导数满足条件
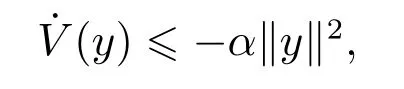
则称系统(9a)是二次渐近稳定的.
下面通过不确定性系统(9a)的二次渐近稳定性分析给出本文的主要结果.
定理1多智能体系统(1)在协议(2)作用下达到通信连接鲁棒状态一致的充分条件是:存在标量ε>0,矩阵Y,对称正定矩阵X >0,使得下列线性矩阵不等式成立:
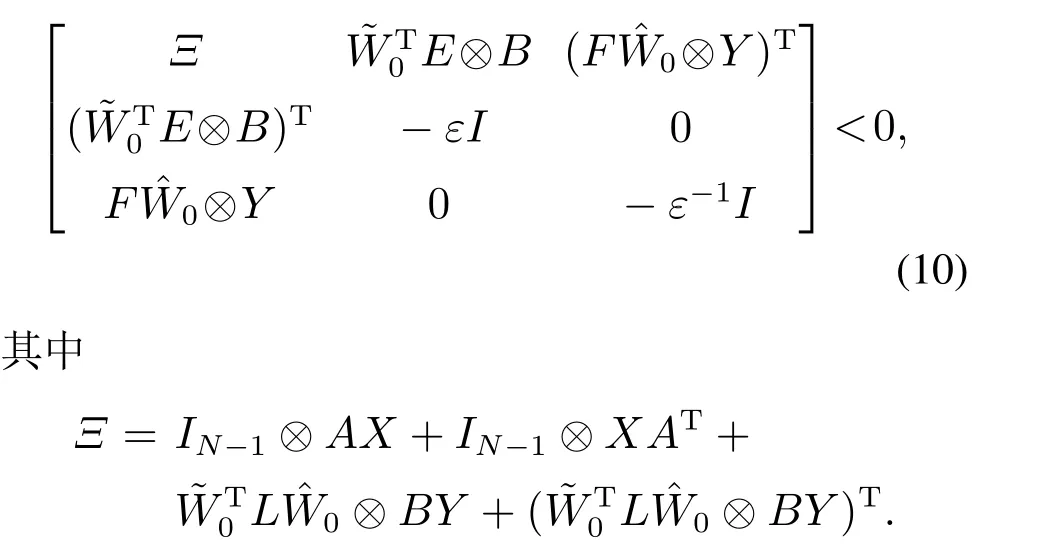
若矩阵不等式(10)的可行解为X和Y,则协议(2)的反馈增益矩阵为K=Y X-1.
证构造如下的Lyapunov函数:
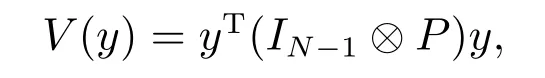
其中矩阵P是正定的,可知Lyapunov函数V(y)是正定的.沿着闭环系统(9a)的任意状态轨迹,V(y)关于时间的导数为


即Q<0时,则具有参数不确定性的系统(9a)是鲁棒二次稳定的.
定义

则矩阵不等式(11)可以写成
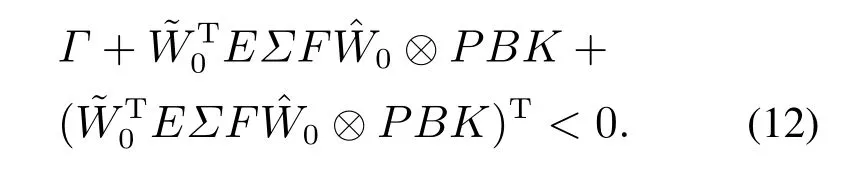
根据引理1的ΔL分解,式(12)可以等价地写成

由引理3,式(13)等价于存在正数ε >0,使得
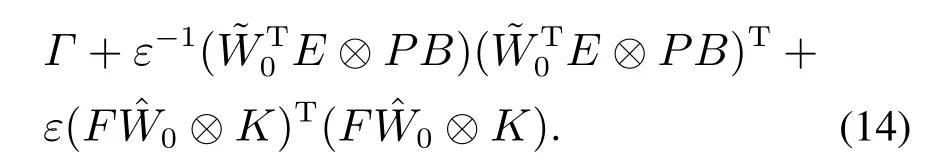
应用引理4,式(14)进一步转化为

表达式(15)中包含有非线性项,因而MATLAB中线性矩阵不等式工具箱无法对其直接求解,针对此情况,需要进行如下等价变化.令
对式(14)分别左乘J,右乘JT,并定义变量
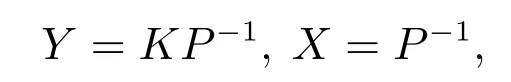
则可得到式(10).由KX=Y 可以得到反馈增益矩阵K=Y X-1. 证毕.
根据定理1,可以得到增益矩阵K的设计过程:
步骤1判断有向图G在标称权值条件下是否存在一棵有向生成树.如条件不成立,则算法终止;
步骤2根据已知的通信拓扑图,求出Laplacian矩阵L,根据引理1对ΔL进行分解;
步骤3求出关联矩阵,根据式(5)可得线性变换矩阵W,并求出逆矩阵W-1;
步骤4利用定理1,根据线性矩阵不等式(10)以及约束条件X >0,求出增益矩阵K.
注3定理1的结果针对一般线性多智能体系统模型和一般有向通信拓扑,结果更一般.此外,文献[17]给出Riccati方程或文献[8,10]给出的不等式条件中,需要预先调整更多参数.有时即使问题本身是有解的,也不易找到满足条件的解.本文给出的条件不需要预先调整参数便可直接求得满足一致性条件要求的解.
5 仿真实例
例1考虑一个含6个智能体的二阶多智能体系统,每个系统的状态空间方程(1)的参数矩阵为
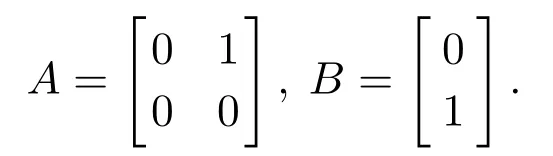
多智能体的有向拓扑图G1和该图的一棵有向扩展树如图1所示.
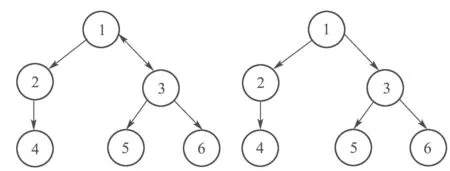
图1 通信拓扑图和有向生成树Fig.1 Communication topology and a directed spanning tree
假设邻居节点之间的权值系数aij=1,即对应于图G1的Laplacian矩阵为

网络通信造成的多智能体互联系统的不确定性ΔL=EΣ(t)F,其中矩阵E和F的参数如下:

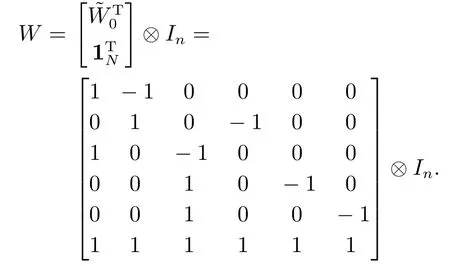
由定理1,当ε=10.4346时,可得控制协议(2)的反馈增益矩阵
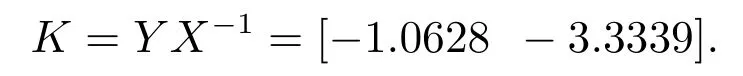
设对角矩阵Σ(t)=diag{q1,···,q6},其中qp为不确定参数,假定满足-1 ≤qp≤1.
为了验证控制算法的可行性,仿真中取
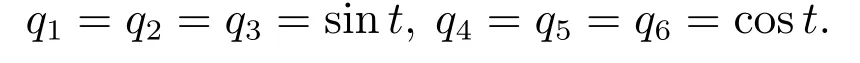
假定系统的初始时刻为t0=0,多智能体系统的初始状态值如下:

线性多智能体系统(1)在信息拓扑图G1下的状态轨迹如图2所示.从图中可以看出,在参数摄动的情况下,6个智能体位置和速度都各自渐近地趋于一致.
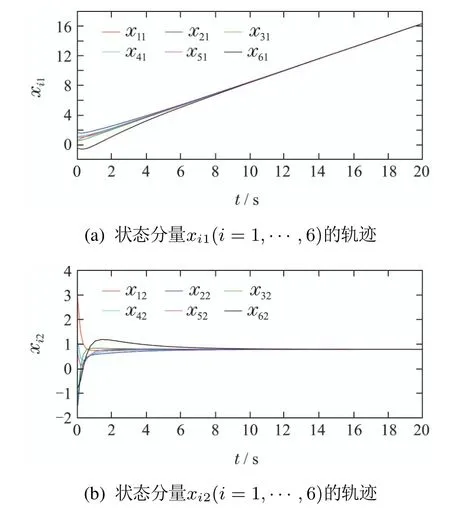
图2 通信不确定多智能体系统的状态轨迹Fig.2 State trajectories of MASs with uncertain communication topology
例2考虑一个三阶多智能体系统,它包含4个智能体且每个系统的状态方程(1)的参数为

多智能体的有向拓扑图G2和该图的一棵有向扩展树如图3所示.
邻居节点之间的权值系数如图3所示,即对应于图G2的Laplacian矩阵为

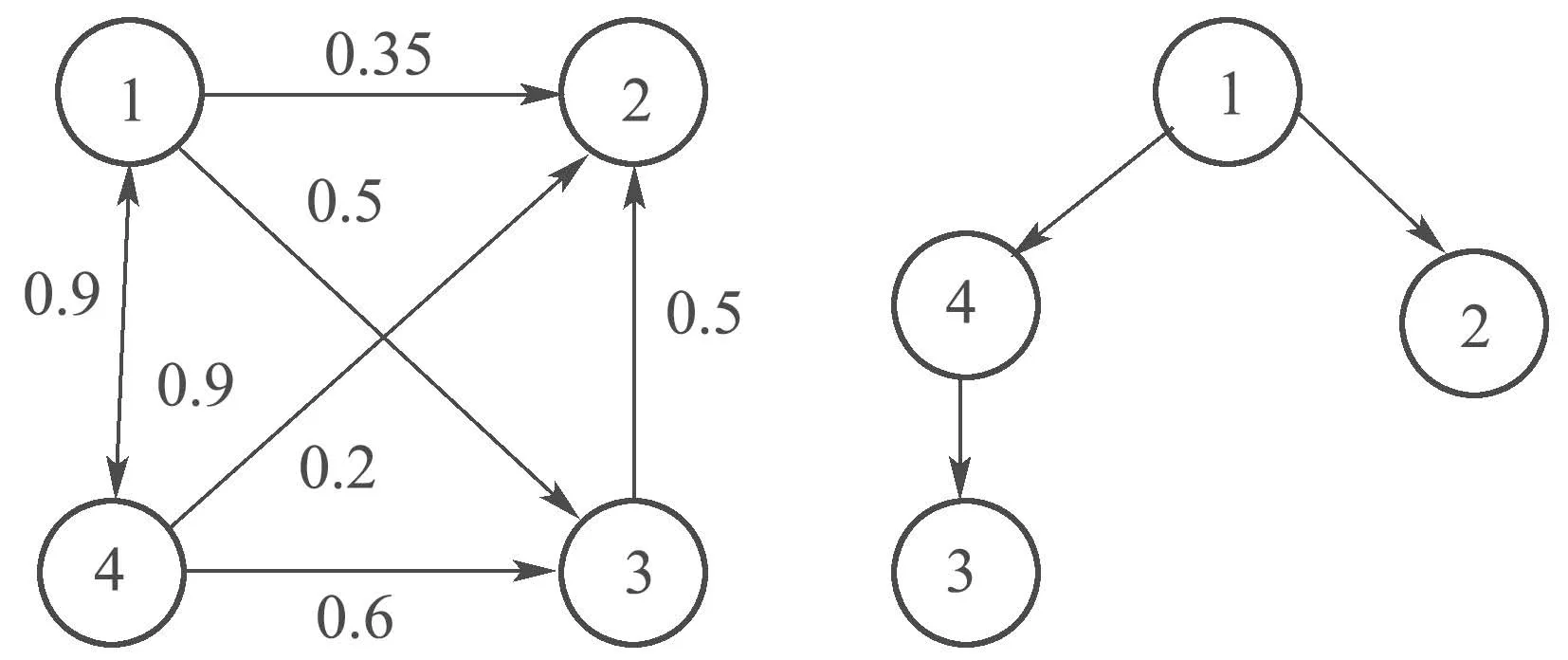
图3 通信拓扑图和有向生成树Fig.3 Communication topology and a directed spanning tree
网络通信造成的多智能体互联系统的不确定性ΔL=EΣ(t)F,其中矩阵E和F的参数如下:

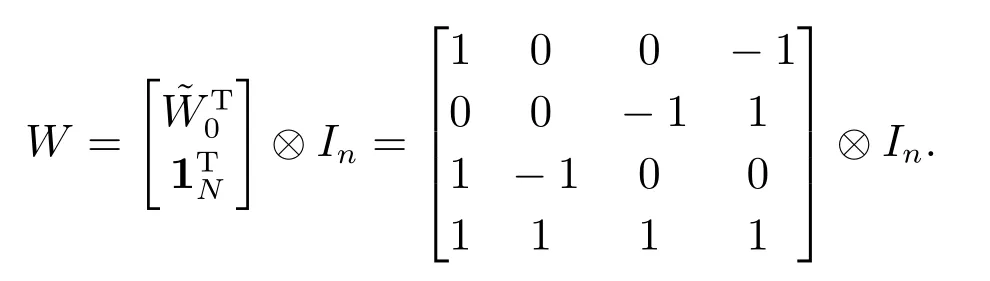
由定理1,当ε=10.4346时,可得控制协议(2)的反馈增益矩阵

取q1= q2= q3= q4=sin t,q5= q6= q7=cos t,多智能体系统的初始状态值如下:

线性多智能体系统(1)在信息拓扑图G2下的状态轨迹如图4所示.图4(a)-(c)分别表示系统的3个状态x1,x2,x3的轨迹,从图中可以看出3个状态最终都趋于一致.进而,数值仿真结果也验证了定理1的正确性.
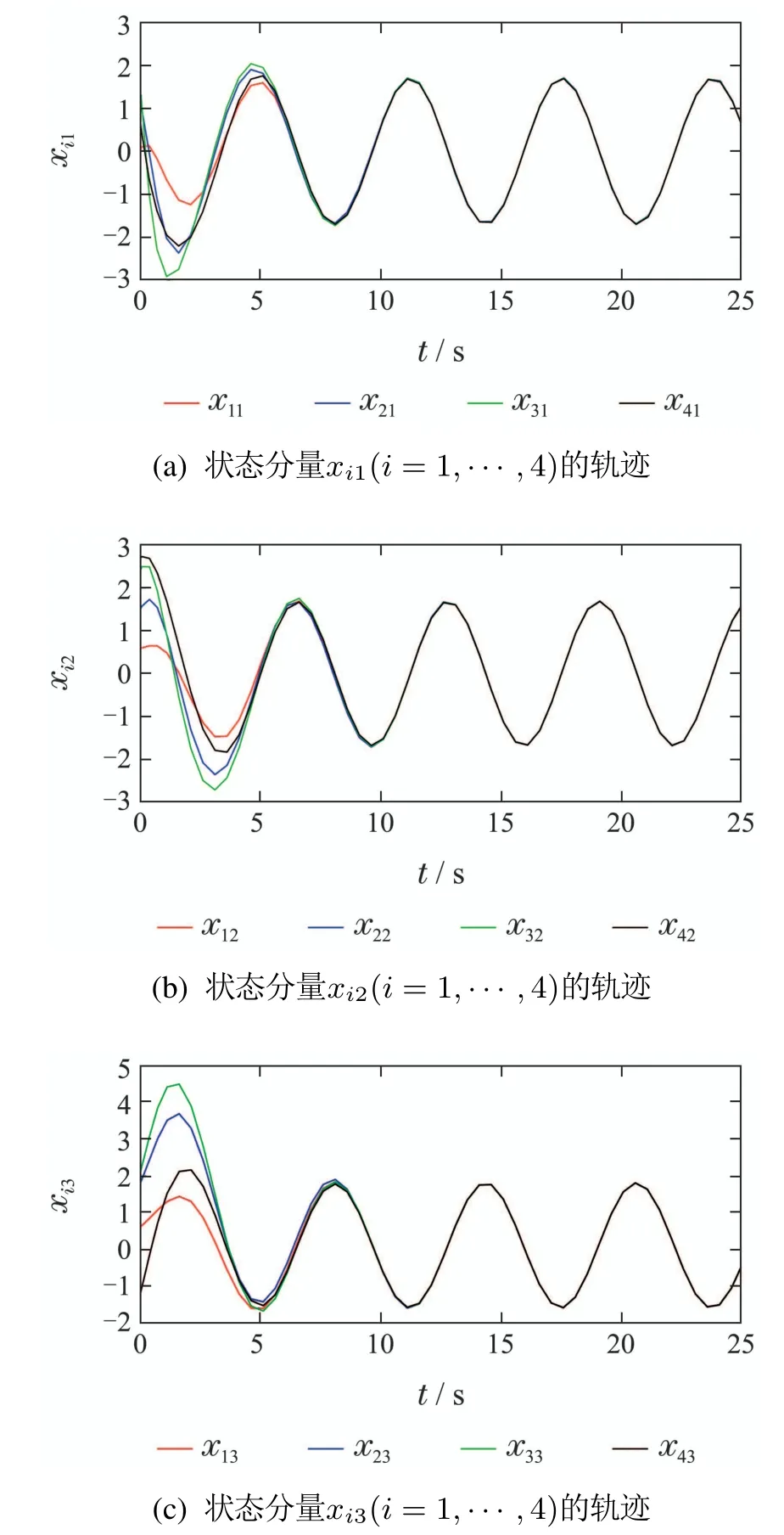
图4 通信不确定多智能体系统的状态轨迹Fig.4 State trajectories of MASs with uncertain communication topology
6 结论
本文针对具有通信不确定的多智能体系统状态一致性问题,提出了鲁棒部分变元稳定性方法.与平均一致性不同,本文采用有向扩展树的关联矩阵进行线性变换,将连续时间多智能体不确定系统的一致性问题转化为不确定系统鲁棒二次镇定问题,其中采用该矩阵进行线性变换,更具有针对性.对摄动矩阵ΔL进行分解,使其满足匹配条件,基于鲁棒二次稳定性理论,分析了系统的稳定性和鲁棒性,在满足系统稳定性的同时,使得所有智能体状态达到渐近一致.仿真结果表明:所提出的部分稳定性方法在参数摄动的情况下,多智能体系统状态分量仍能各自渐近地达到一致,误差逼近于零,从而实现了多智能体系统协调控制的目的.
值得指出的是,本文所提出的方法利用了全局信息,然而在实际的分布式控制中全局信息是未知的,后续研究工作将进一步考虑利用局部信息,将智能体i及其通信邻居集合的一致性问题转化为鲁棒部分变元稳定性问题,其余智能体转化为领导-跟随多智能体的一致性问题,从而设计反馈增益矩阵,实现真正意义上的分布式控制.
