系统直和博弈模型下的合作演化

李亚昆，冯俊娥

(山东大学数学学院，山东济南 250100)

1 引言

演化博弈论是将生物进化论与经典博弈论结合产生的理论，是博弈论中新的发展方向，其已经成为研究合作演化行为的有力工具.达尔文在《物种起源》一书中提到:动物的本能是趋利避害.在博弈的过程中，个体会为了最大化自身的利益而选择背叛策略.从这个层面上讲，合作行为似乎是不可能存在的，然而合作现象却处处可见，例如蝙蝠之间的喂食行为，企业乃至国家的战略联盟等等.这显然与达尔文的思想之间存在矛盾，因此探究合作演化行为对目前世界上很多现实问题都具有深刻的意义.

演化博弈论主要研究种群演化的动态过程，集中分析演化稳定策略[1]和复制者动力学，这两个核心问题分别描述了演化稳定状态及趋于稳定的收敛过程.1973年，Smith和Price在“The Logic of Animal Conflict”中提出演化稳定策略，标志着演化博弈理论正式诞生.复制者动力学是由Taylor和Jonker在1978年提出的，他们给出了研究种群演化的复制者方程[2].这两项工作为合作演化的研究提供了理论基础.随后学者们以演化博弈论为基础对合作演化行为做了大量的研究.从合作机制上囊括了如下情形:亲缘选择[3]、直接互惠[4]、间接互惠[5]、空间互惠[6]、群组选择[7]等等.除此之外，文献[8]研究了共演化动力学对合作演化的影响.文献[9]中建立了多人雪堆模型，对多人合作的演化动力学进行了研究.文献[10]研究了复杂系统中引入激励机制对合作演化行为的影响.研究发现，正激励可以抑制负激励的负面影响，从而使合作行为涌现.

近些年来，一种新兴的矩阵方法―矩阵半张量积，广泛运用于博弈论研究中，已成为研究博弈控制论这个交叉领域有力的工具[11].文献[12]指出利用半张量积可将博弈论中一些重要的公式定理转化为代数形式，从而得出一些有趣的结果.在这个代数框架下，文献[13]研究了对称博弈的空间内部结构.文献[14]给出了模糊关系不等式具体的求解算法.文献[15]将该代数框架推广到具有破产机制的演化博弈，并研究其演化动力学行为.文献[16]研究了一类具有短视最优规则的网络演化博弈的动力学行为，并给出了构造博弈代数方程的算法.文献[17]给出了实现策略一致的最小控制问题的充要条件.文献[18-19]分别讨论了竞争扩散博弈的纳什均衡和动态演化博弈的策略优化问题.文献[20-21]则分别给出了判断有序势博弈的算法和Banzhaf值的等价代数形式.文献[22]对矩阵半张量积在有限博弈中的应用做了较系统的介绍，它本质上与多值逻辑[23]类似.这些结果表明，矩阵半张量积在研究演化博弈的动力学以及策略优化问题等方面有着重要的作用.

纵观之前的工作，大多数都是从局部的角度来研究合作演化问题，仅仅考虑了一种博弈方式.然而现实世界纷繁复杂，各种事物之间紧密联系.每个个体都会参与多种活动，并且在不同的活动中获得不同的收益.个体在参加博弈时，在每种博弈下获得最大收益时，整体收益可能并不是最优的.参加博弈者不仅仅只需要考虑在这一次活动中获得的收益，而是要从整体来看个体自身所获得的总收益.这就要求从全局的角度来研究合作演化问题.

本文讨论以石头剪刀布和雪堆模型为基础，采用矩阵直和的形式构建系统直和博弈模型[24].此模型通过引入参数，增加了相同博弈模型支付矩阵的多样化.随后将其推广到了n个博弈方式，使模型的适应性更广，更加具有现实意义.最后根据博弈过程，将直和矩阵转化为含参数的系统总支付矩阵.利用MATLAB对系统直和博弈模型进行仿真模拟，从全局的角度即系统整体对合作演化进行研究.

本文的难点在于将直和矩阵转化为含参数的系统总支付矩阵.在系统直和博弈模型的推广中，随着博弈方式及策略数量的增加，系统总支付矩阵的参数及维数均增加.本文中系统总支付矩阵的维数代表种群中个体类型的数目，维数增加即种群中个体类型增加，从而增大了仿真模拟的难度，使模型的求解分析更为复杂.因此准确的确定系统总支付矩阵是本文的关键.

2 预备知识

1978年，Taylor和Jonker提出了复制者动力学的概念，将动态演化过程与演化博弈论有效结合起来，进一步丰富了演化博弈论的内涵.复制者动力学是对种群策略演化过程的宏观分析，是博弈论动力学的连续确定方程.复制者方程如下所示:

其中:Xi为策略类型i的比例;A为支付矩阵;ei为第i位是1、其余均为0的行向量;eiAXT为采用策略类型i的总收益;XAXT为种群的平均收益.

2.1 基于双人双策略对称博弈的种群演化动力学

文献[25]基于群体结构和多人交互作用等影响因素对种群的合作演化进行了深入的研究.本节首先以双人双策略对称博弈为例，运用复制者方程研究种群的演化动力学过程.每个个体都有两种策略:合作策略C和背叛策略D.其中:若双方都选择C时，二者收益相同均为R;若有一方选择C而另一方选择D，则选择C的收益为S，而选择D收益为T;若双方都选择D时，二者收益相同均为P.双人双策略对称博弈的支付单矩阵如表1所示.

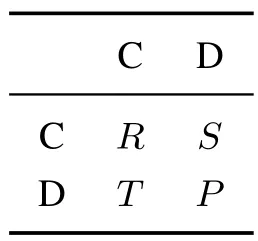
表1 双人双策略对称博弈的支付单矩阵Table 1 Payment order matrix of two-person two strategies symmetric game

假设种群中选择C策略个体的比例为x，选择D策略个体的比例为y.此时X=[x y]，因此利用复制者方程得到下式:

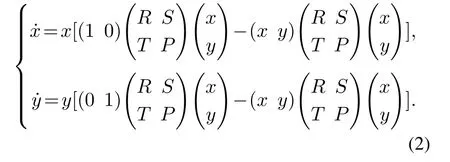
结合实际，可知x+y=1.由此减少变量，得到关于x的动力学微分方程，从而为研究不同参数下x的动态演化过程提供了动力学依据.

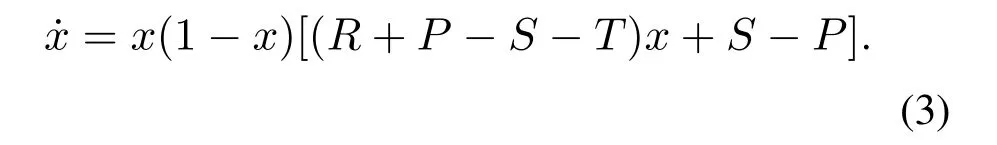
不同的参数代表了不同的博弈模型.参数不同，动力学特征不同，动态演化过程也不同.接下来为了进一步分析在不同参数取值下策略选择均衡点的演化过程，利用MATLAB进行仿真模拟，得到图1的4条演化轨线，并进行相应的分析.

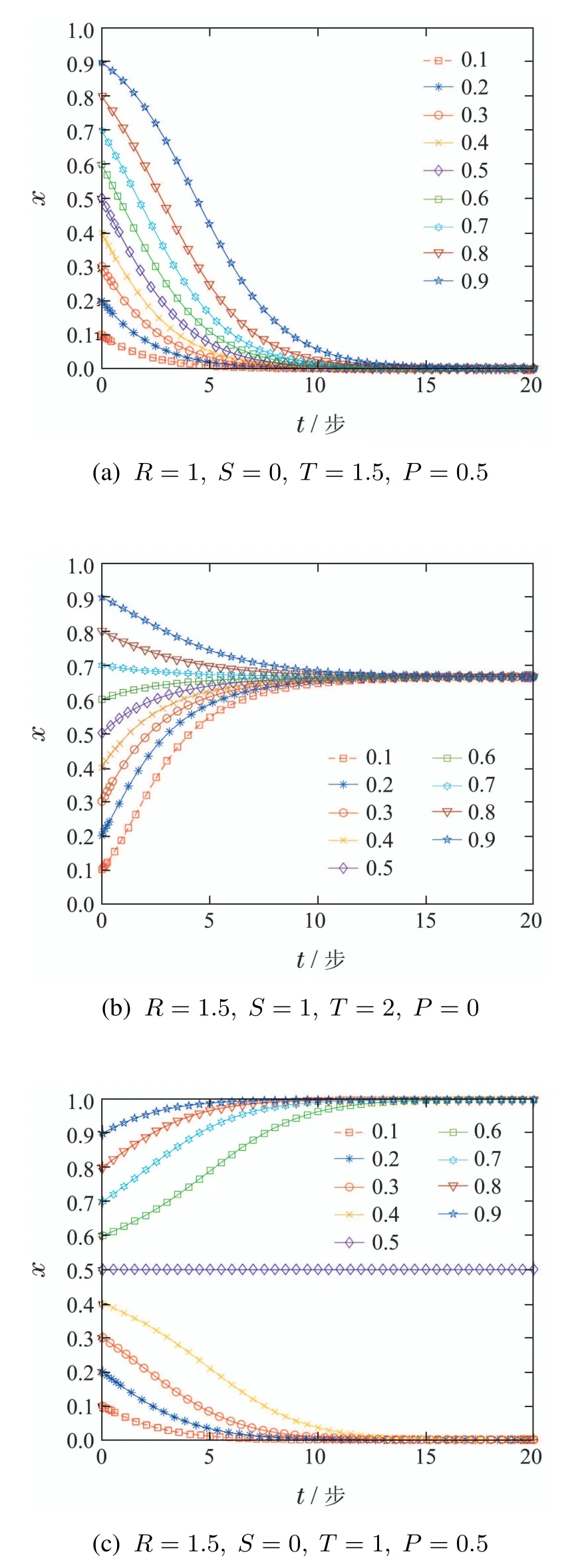
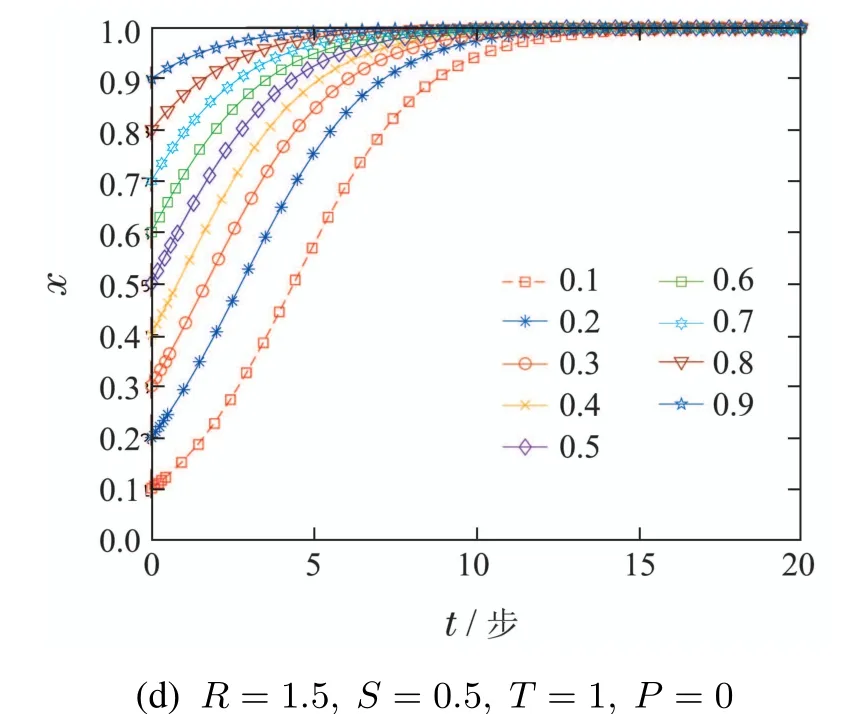
图1 不同参数下X的动态演化图Fig.1 The dynamic evolution of X under different parameters

1)给定参数R=1，S=0，T=1.5，P=0.5，满足T ＞R＞P ＞S，代表博弈模型为囚徒困境等.图1(a)展现了在不同初值下，演化轨线随着时间的推移向平衡点x=0趋近的过程，因此参数满足上述关系的演化稳定策略为x*=0，表示种群在演化的过程中，不论初值的大小，D策略总是作为优势策略逐渐增加，C策略逐渐减少，直至为0.并且x的初值越大，减少的速度越快.

2)给定参数R=1.5，S=1，T=2，P=0，满足T＞R ＞S ＞P，代表博弈模型为雪堆模型、鹰鸽模型等.图1(b)展现了在不同初值下，演化轨线随着时间的推移从两头向平衡点趋近的过程，因此参数满足上述关系的演化稳定策略为，表示种群在演化的过程中，若初值x ＜x*，则x不断增加，直至达到平衡点.反之x不断减少，直至达到平衡点.并且初值与平衡点差距越大，变化速度越快，最终的稳态是两种策略以一定的比例共存.

3)给定参数R=1.5，S=0，T=1，P=0.5，满足R ＞T ＞P ＞S，代表博弈模型为猎鹿博弈、性别大战等.图1(c)展现了在不同初值下，演化轨线随着时间的推移向两头x=0，x=1趋近的过程，因此参数满足数量关系的演化稳定策略为x*=0，x*=1，表示种群在演化的过程中，不同的初值会呈现出不同的演化轨迹，在种群中占比更高的策略随着时间的推移会变成优势策略，直至为1.

4)给定参数R=1.5，S=0.5，T=1，P=0，满足R ＞T ＞S ＞P.图1(d)展现了在不同初值下，演化轨线随着时间的推移向平衡点x=1趋近的过程，因此参数满足上述关系的演化稳定策略为x*=1，表示种群在演化的过程中，不论初值的大小，C策略总是作为优势策略逐渐增加，D策略逐渐减少，直至为0.并且x的初值越小，增加的速度越快.

2.2 基于双人三策略对称博弈的种群演化动力学

在研究种群演化动力学时，人们发现双人双策略的博弈有时候并不能解释一些自然现象，例如斑点蜥蜴循环捕食和大肠杆菌3种亚种循环竞争制约的现象.在现实生活中，两个个体进行策略选择时，不仅仅包含合作与背叛两种策略，还有的个体会选择消极合作等中立态度.因此拓展现有的博弈模型具有现实意义.Hauert等人[26-27]提出了拓展的囚徒困境模型，即在囚徒困境中引入第3种策略E.研究发现引入策略之后，此时的优势策略不再是背叛策略，而是3种策略循环占优，类似于常见的“石头剪刀布”博弈.“石头剪刀布”博弈中呈现出来的循环占优现象是维持生物多样性的重要机制.

下面以“石头剪刀布”博弈为例，研究双人三策略对称博弈的演化动力学.研究方法与第2.1节相同.假设选择C策略的比例为p，选择D策略的比例为q，选择E策略的比例为r.基于复制者方程可得下式:

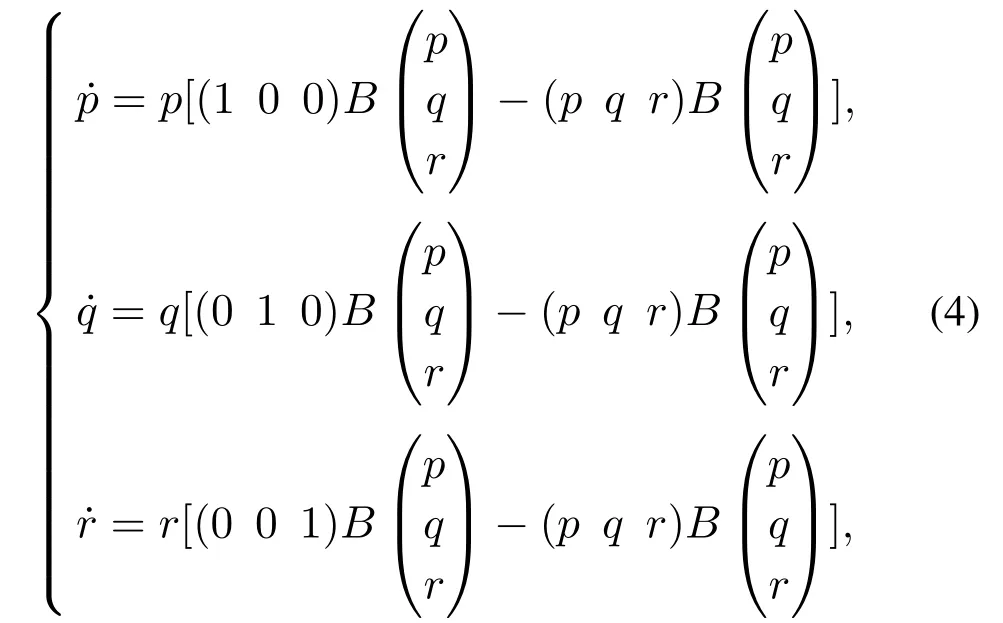
其中B为石头剪刀布博弈的单一支付矩阵:

由于p+q+r=1，由此减少变量，得到关于p，q的动力学微分方程，从而为研究不同参数下p，q的动态演化过程提供了动力学依据.减少参数化简为

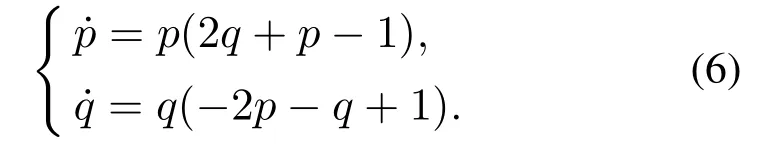
初值不同，动态演化过程也不同.接下来为了分析在不同初值下策略选择均衡点的演化过程，本文利用MATLAB进行仿真模拟，得到图2的4条演化曲线，发现在不同的初值下，没有哪一种策略总是占据主导地位，3 种策略是循环占优、互相制约的.这种现象是维持生物多样性的基础，从而使得整个系统更加稳定.不仅如此，通过对比发现，在演化开始前，3种策略的选择概率越是接近，在演化过程中的波动越小.由此可知，在其他博弈模型可以引入更多的策略，从而更好地解释合作行为的演化过程.

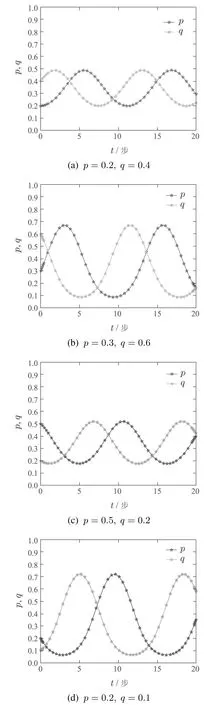
图2 石头剪刀布博弈中X的动态演化图Fig.2 The dynamic evolution of X in rock-paper-scissors game

3 模型的建立与推广

博弈模型多种多样，反映了现实中不同类型个体相互作用的多样性.在现实生活中，每个个体都会参加多个活动，即参加多种博弈.这就要求从全局的角度来研究系统整体的收益，更好地为每次策略选择提供依据，因此研究系统直和博弈模型有重要的意义.接下来以石头剪刀布博弈模型和雪堆博弈模型为例，首先构建单参数的支付矩阵，然后采用矩阵直和的形式建立系统直和博弈模型.

3.1 构建单参数的支付矩阵

双策略博弈的单支付矩阵包含4个参数，三策略博弈则包含9个参数，策略增加，参数也随之增加.若基于目前的支付矩阵来构建系统直和博弈模型，就会产生太多参数，大大提高了分析的难度.因此需要构建单参数支付矩阵便于分析.

Nowak和May在文献[28]中提出将收益矩阵进行归一化的方法.归一化是指将不同变化范围的值映射到相同的固定范围中，选定的范围是[0，1]或[－1，1].本文选定范围为[－1，1].构建单参数的支付矩阵指通过归一化的方法将原来含有多个参数的支付矩阵转换为仅含一个参数.这个参数代表背叛诱惑因子，取值范围为[0，1].单参数支付矩阵的构建原则是不改变策略收益之间的数量关系，能够较好的表征模型的演化行为，从而不影响实验结果.

1)石头剪刀布博弈模型[29].

石头剪刀布博弈的单参数支付矩阵可以表示为

在上式中，参数α ∈[0，1]，表示在赢得博弈时获得的收益.参数不同，支付矩阵不同，实现了在相同博弈模型下支付矩阵的多样性，使其更有研究意义.通过调整参数值，进一步深入研究演化过程的变化.

2)雪堆博弈.

对于雪堆博弈，甲、乙两个人开车相向而行，途中被一个雪堆挡住了回家的去路.假设道路通畅后的收益为b，铲雪需要付出的劳动量为c.因此雪堆博弈的收益矩阵可以表示为

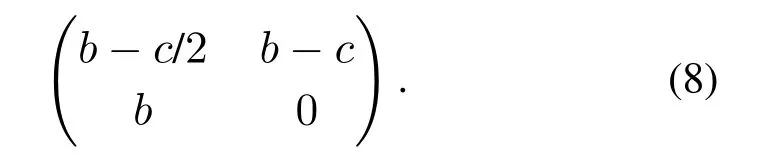
将上面的收益矩阵进行归一化变换后，表示为

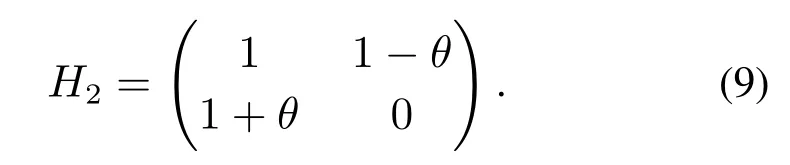
在上式中，参数θ ∈[0，1].单参数支付矩阵满足雪堆博弈模型中对应的大小关系:T ＞R ＞S ＞P.其中θ=c/(2b－c)，是雪堆模型收益矩阵中唯一的参数，代表了个体的付出和收益的比率.

3.2 建立系统直和博弈模型

现在考虑一个系统，假设每个个体参与两种博弈，分别是石头剪刀布博弈和雪堆博弈.当系统中的个体与其他个体之间进行博弈时，第1步选择博弈类型.第2步选择策略来进行第1步中选择的博弈类型.

在一个两两互相作用的博弈中，通过引入参数来表示第1步中选择博弈方式的概率.假设每个个体选择进行石头剪刀布博弈的概率为r1，选择进行雪堆博弈的概率为r2，并且r1+r2=1.引入参数之后构建系统直和博弈模型.

接下来通过矩阵直和的方法构建系统直和博弈模型的直和矩阵.直和矩阵如下所示:

其中:直和矩阵实际上为分块矩阵，对角线分别为石头剪刀布博弈和雪堆博弈的支付矩阵H1，H2，另一条对角线为子矩阵0.由于选择不同的博弈方式的个体是不能进行相互作用的，因此在直和矩阵中用子矩阵0来表示.

石头剪刀布博弈有3种可供选择的策略，分别是C策略、D策略、E策略;雪堆博弈有两种策略，分别是c策略、d策略.依据上述建立的系统直和博弈模型可知，系统直和博弈模型中的个体共分为6种类型，分别记为Cc，Cd，Dc，Dd，Ec，Ed.其中:Cd 是指这种类型的个体在石头剪刀布博弈中采用C策略，在雪堆博弈中采用d策略.其他5种类型的符号含义类似.因此这6种策略的总支付矩阵如下所示:

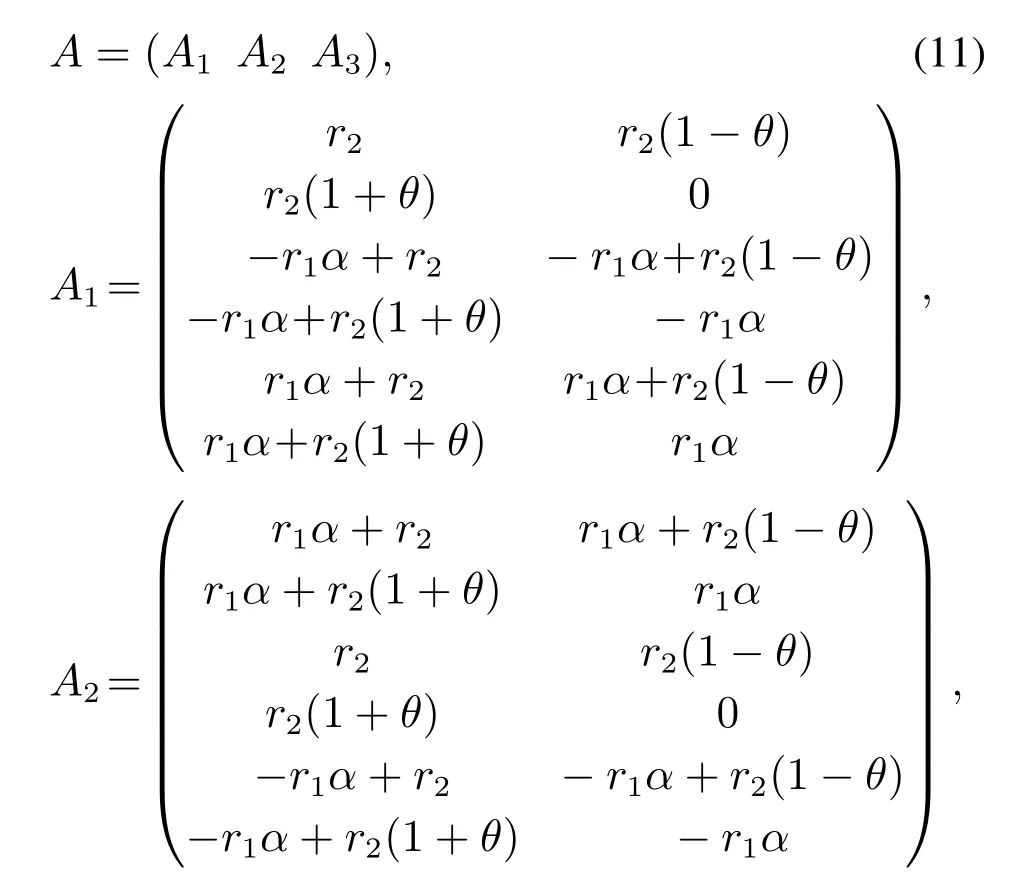
6种类型的排列顺序直接影响总支付矩阵中每一个位置所代表的实际含义.在本文中，采用的排列顺序是先取定第1种博弈模型的第一种策略，然后分别遍历第2种博弈模型的所有策略.遍历完成后，再取定第1种博弈模型的第2种策略，依次进行.因此6种类型的排列顺序依次为Cc，Cd，Dc，Dd，Ec，Ed.其中A1矩阵中第1行第2列的含义是系统中Cc类型和Cd类型的个体发生博弈时，Cc类型的个体获得的总收益.其余的含义类似.

3.3 系统直和博弈模型的推广

本节基于上述模型的建立过程，为了使模型的适用范围更广，现将系统直和博弈模型推广到n个博弈方式，每种博弈方式包含的策略也是任意的.

定理假设n个博弈方式的单参数支付矩阵分别为H1，H2，···，Hn，每种博弈方式包含的策略数目分别为m1，m2，···，mn，个体在选择博弈类型时的概率分别为r1，r2，···，rn.直和矩阵的维数为m，系统直和博弈模型的总支付矩阵的维数为M.系统直和博弈模型的总支付矩阵记为AM×M:

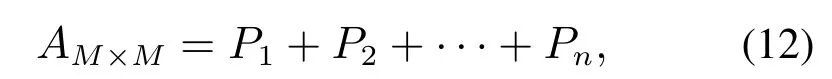
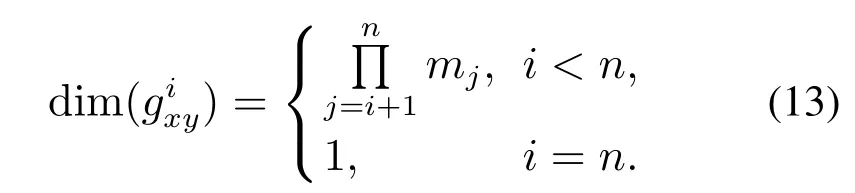
分析过程如下所示:

首先利用单参数支付矩阵构建系统直和博弈模型的直和矩阵，如下所示:

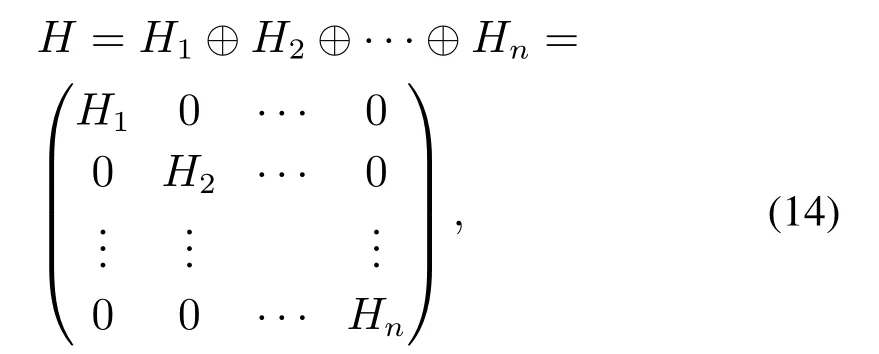
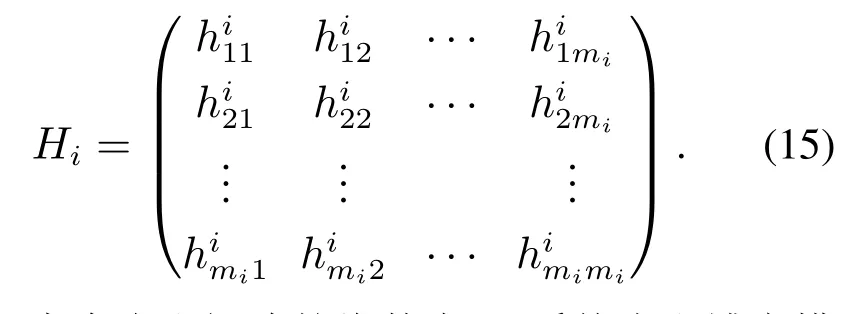
接下来令直和矩阵的维数为m，系统直和博弈模型的总支付矩阵的维数为M，m和M满足下式:

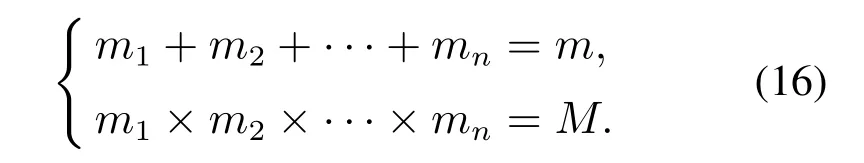
随后利用直和矩阵求出系统直和博弈模型的总支付矩阵AM×M:

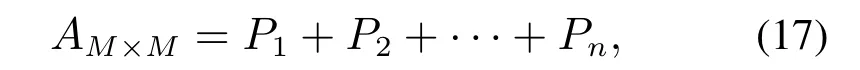
其中Pi是分块矩阵，分块矩阵的块数为每块均为Gi.设Gi中的元素为，即，x，y=1，2，···，mi.其中是方阵，维数用来表示.

最后将总支付矩阵AM×M代入复制者方程中，得到系统中不同类型个体的演化方程.

注1在系统直和博弈模型的推广中，总支付矩阵的维数M即为种群中个体类型的数量.m1×m2×···×mn=M代表种群中个体类型的数量为每种博弈方式的策略数量之积.因此在第3.2节中，石头剪刀布博弈有3种策略，雪堆博弈有两种策略，所以种群中有6种类型的个体.

注2种群中个体类型的划分标准为在博弈方式中选择的策略.在第3.2节中，Cd是指这种类型的个体在石头剪刀布博弈中采用C策略，在雪堆博弈中采用d策略.先选雪堆博弈，后选石头剪刀布博弈对结果没有影响，因此不需要考虑选择博弈类型的顺序.

4 模型的求解与分析

本节基于复制者方程给出系统直和博弈模型的总支付矩阵的演化方程，如下所示:

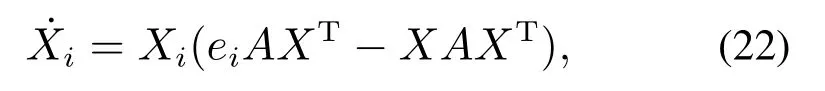
式中:X=[x1x2x3x4x5x6]，x1，x2，x3，x4，x5，x6分别表示6种类型Cc，Cd，Dc，Dd，Ec，Ed在系统中所占的比例，并且满足x1+x2+x3+x4+x5+x6=1;A为上节得到的系统直和博弈模型的总支付矩阵.

首先假定X=[0.2 0.2 0.2 0.2 0.1 0.1]，分别表示系统中Cc，Cd，Dc，Dd，Ec，Ed等6种类型个体的初始比例为0.2，0.2，0.2，0.2，0.1，0.1.其次对其他参数α，θ，r1，r2设定不同的值，观察在不同的参数下不同类型个体的演化过程，从而得出有意义的结论.图3是运行时间步为1000的典型模拟结果.

图3 不同参数下下X的动态演化Fig.3 The dynamic evolution of X under different parameters

图3(a)设定参数[α，θ]=[1，0]，[r1，r2]=[1，0].实际意义为所有个体均选择了石头剪刀布模型.由图3(a)可知:C，D，E三种策略循环占优，相互制约，与上述石头剪刀布博弈的演化动力学研究的结论基本相同.

图3(b)设定参数[α，θ]=[0，1]，[r1，r2]=[0，1].实际意义为所有个体均选择了雪堆模型.由图3(b)可知:Cd，Dd和Ed三种类型的个体逐渐增加并趋于稳定，Cc，Dc，Ec则逐渐减少并趋于稳定，最终c策略和d策略以一定的比例共存，且d策略的比例更高，与上述雪堆博弈的演化动力学研究的结论基本相同.

通过图3可知，系统直和博弈模型同样适用于单一博弈模型.通过控制参数的值来实现系统直和博弈模型单一化.

图4(a)设定参数[α，θ]=[0.3，0.7]，[r1，r2]=[0.5，0.5]，实际意义为选择两种模型的比例均为0.5，石头剪刀布模型中赢得比赛的收益为0.3，雪堆博弈模型中不下车获得的补偿为0.7.图像表明波动幅度不大，并且在运行1000步后与初始值大致相同.图4与图3相比即混合之后的系统直和博弈较单一博弈相比，合作策略的占比明显增加，且整个系统稳定性更好，更适于生存.很好地解释了合作行为广泛存在的现象.

图4(b)设定参数[α，θ]=[0.1，0.9]，[r1，r2]=[0.5，0.5]，实际意义为选择两种模型的比例均为0.5，石头剪刀布模型中赢得比赛的收益为0.1，雪堆博弈模型中不下车获得的补偿为0.9.较图4(a)相比，该参数下各种类型的个体的比例在运行1000步后变化较大，Cc，Dc，Ec呈下降趋势，其余类型呈现上升趋势.这种现象表明在选择模型比例相同的情况下，θ占比较大，因此第2种模型占据主导地位.从整体来看，合作策略的稳定性有所下降，更有利于背叛策略的演化.由此可知α和θ即支付矩阵的变化直接影响系统直和博弈模型中的各个类型个体的演化过程.

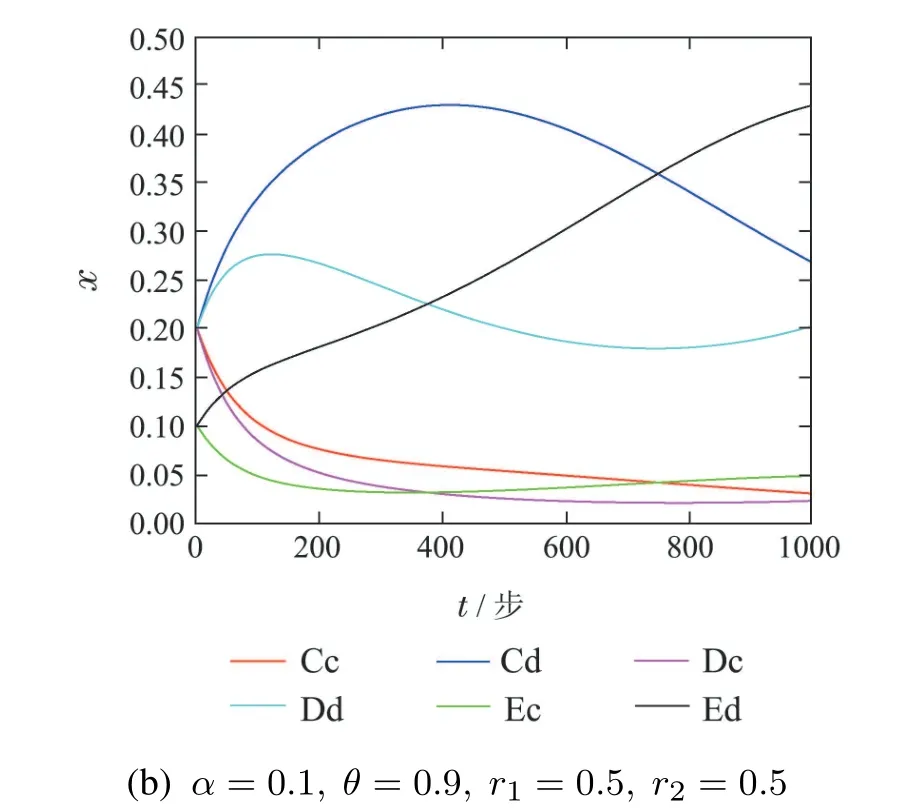
图4 不同参数下下X的动态演化Fig.4 The dynamic evolution of X under different parameters

图5(a)设定参数[α，θ]=[0.1，0.9]，[r1，r2]=[0.9，0.1]，实际意义为选择石头剪刀布模型的比例为0.1，选择雪堆模型的比例为0.9.石头剪刀布模型中赢得比赛的收益为0.9，雪堆博弈模型中不下车获得的补偿为0.1.较图4(b)相比，该参数下，各种类型的个体比例在运行1000步后会有较小的变化.由此可知r1，r2即选择博弈方式的概率也会直接影响系统直和博弈模型中的各个类型个体的演化过程.

图5(b)设定参数[α，θ]=[0.9，0.1]，[r1，r2]=[0.1，0.9]，实际意义为选择石头剪刀布模型的比例为0.9，选择雪堆模型的比例为0.1.石头剪刀布模型中赢得比赛的收益为0.1，雪堆博弈模型中不下车获得的补偿为0.9.较图4(b)和图5(a)相比，该参数下，各种类型的个体在运行1000步后与初始值大致相同.由此需要从全局来看，α，θ为单参数支付矩阵中唯一的参数，实际意义为背叛诱惑因子.r1，r2表示选择模型的概率.从全局来看，选择模型的概率小，背叛诱惑因子大或者选择模型的概率大，背叛诱惑因子小.这两种情形下建立的系统直和博弈模型同样能够有较强的稳定性，由此可知α，θ，r1，r2共同影响演化过程.

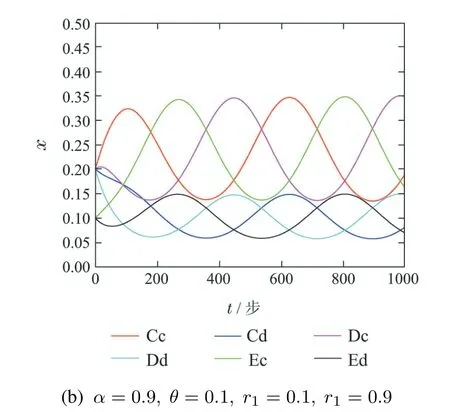
图5 不同参数下X的动态演化图Fig.5 The dynamic evolution of X under different parameters

图6参数为[α，θ]=[0.5，0.5]，[r1，r2]=[0.5，0.5]，在参数一定的情况下，观察不同的初值下各个类型个体的演化过程.由图可知，当系统中有些类型初值为0，其他类型的个体的变化曲线波动较大，甚至会导致有些类型的个体减少至0，系统的稳定性就会下降.因此生物多样性更有利于系统的稳定.

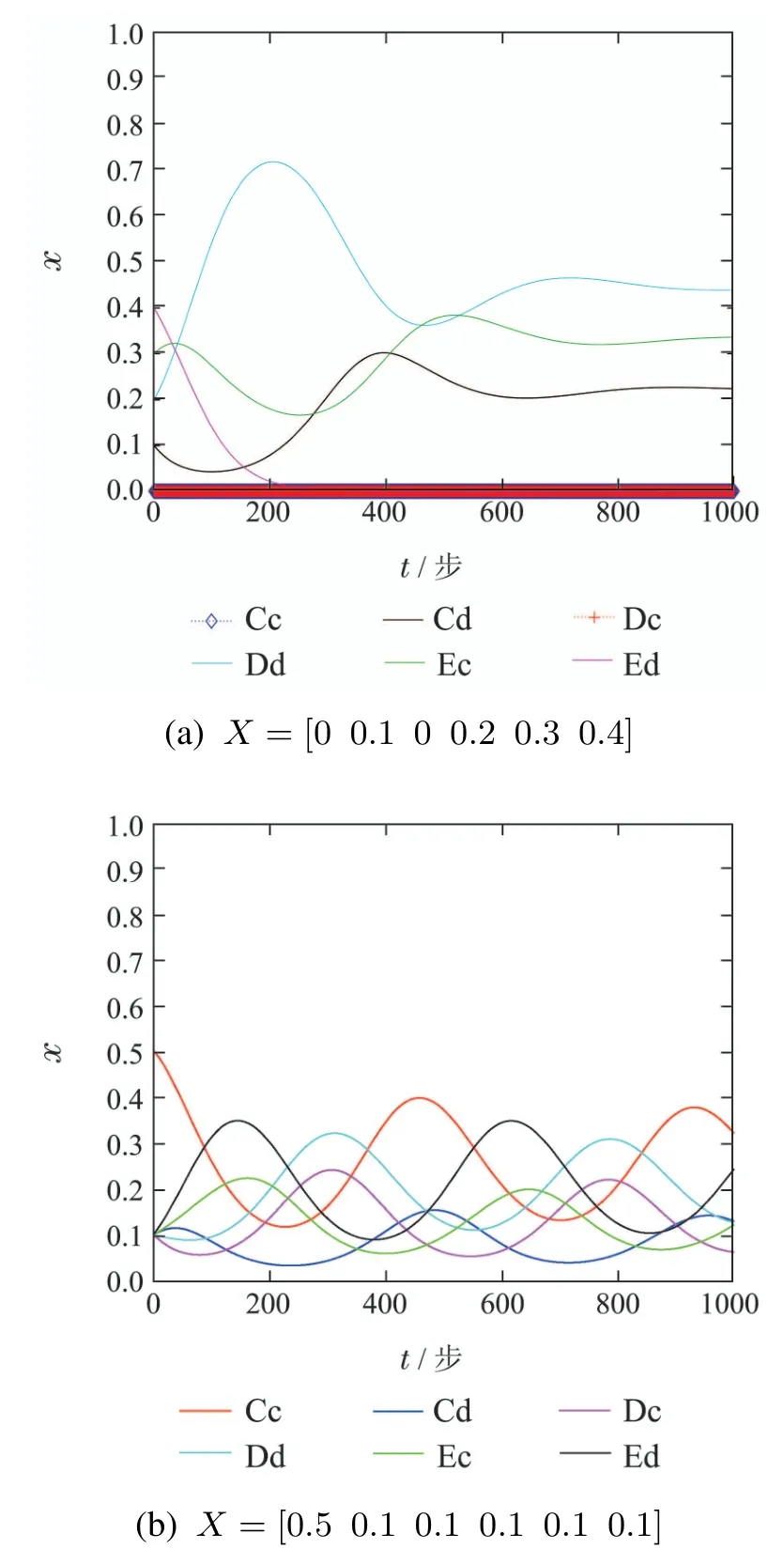
图6 不同初值下X的动态演化图Fig.6 The dynamic evolution of X under different initial values

综上所述，直和博弈较单一博弈而言，合作策略的占比明显增加，且整个系统稳定性更好.很好地解释了合作行为广泛存在的现象.这表明在石头剪刀布博弈中选择弱势策略造成的损失，可以在雪堆博弈中选择不下车作为补偿，使得整体收益最佳.对某些个体而言，在不同博弈中选择不同的策略会实现收益最大化.因此在研究博弈时，需从全局的角度去思考策略的选择.这种合作演化机制称之为全局互惠.这样很好地解释了为什么有些策略在单一博弈中是劣势策略，仍然会有个体选择.因为它们不仅考虑这一次博弈中所获得的收益，而是从全局的角度去考虑.α，θ，r1，r2共同影响系统直和博弈模型中的各个类型个体的演化过程.通过控制参数值，使整个系统更加稳定，也可以通过调整参数值来研究单一博弈的演化过程.不仅如此，通过研究不同初值下的演化过程可知，生物多样性更有利于系统的稳定.由此可见研究系统直和博弈模型对合作演化的研究具有一定的意义.

5 总结

本文基于石头剪刀布模型和雪堆博弈模型，采用矩阵直和的形式构建了系统直和博弈模型，并将其推广到n个博弈方式.给定初值利用MATLAB对系统直和博弈模型进行仿真模拟，从全局的角度来研究合作演化问题，得出全局互惠的合作演化机制，并且得知α，θ，r1，r2等参数共同影响系统直和博弈模型中的各个类型个体的演化过程.对于参数具体对演化过程的影响仍有待于我们今后进一步的研究.正如引言中所述，矩阵半张量积在博弈中的应用已初见端倪，那么如何借助矩阵半张量积的方法构造多个个体共同博弈的系统直和博弈模型也是一个有意义的课题.