基于二维系统的迭代学习事件触发鲁棒控制

余 威，卜旭辉，梁嘉琪

(河南理工大学电气工程与自动化学院，河南焦作 454000)

1 引言

迭代学习控制方法[1-4](iterative learning control，ILC)于1984年由日本学者Arimoto等人提出，是一种针对有限时间区间执行重复控制任务系统的有效控制手段.由于其具有结构简单、不依赖被控系统的精确模型等优点，经过30余年的发展，迭代学习控制算法已经得到了广泛的应用，如机器人[5]、交通控制[6]以及多智能体系统[7]等，对迭代学习控制算法的理论研究也取得了大量的成果[8-11].

网络控制是集通信网络与控制于一体的分布式控制系统，与传统的点对点控制系统相比，具有成本低、结构灵活等优点.近年来，随着网络控制技术的发展，网络环境下的迭代学习控制也有了丰富的研究成果:文献[12]针对具有不确定扰动和区间时变时滞的批处理过程，提出了一种结合迭代学习控制的鲁棒反馈方法.文献[13]提出了一种基于量化误差信息的线性和非线性离散系统迭代学习控制算法.为了抑制随机噪声和量化误差的影响，在算法中引入了一个递减的学习增益.针对单轮移动机器人的鲁棒跟踪问题，文献[14]首先考虑信道噪声的影响，建立非线性系统模型来描述由微分型迭代学习控制器控制的移动机器人，然后推导了控制器端输入误差与信道噪声之间的关系.

以上文献中采用的迭代学习控制算法总是在每个迭代时刻进行更新，即采用传统的时间触发通讯机制.从系统设计和分析的角度，这种机制比较容易实现，但是当考虑到通讯信道的有限带宽问题时就存在一些局限性.如若系统在相隔两次采样时间内，系统信息变化较小时，仍然固定的更新控制信号，则不可避免的会传输许多冗余信息.因此本文为了节约有限的网络资源，降低控制成本，考虑一种带有事件触发机制的迭代学习控制算法.所谓事件触发机制[15-19]就是在保证闭环系统性能的前提下，在满足事先设计的触发条件之后，执行器即执行控制任务.这种基于事件的通信策略已经在理论和实践研究中得到了广泛的关注，文献[20]介绍了根据触发条件进行传感和驱动的事件和自触发控制系统，介绍了这些控制策略的基本原理，并讨论了状态反馈和输出反馈之间的区别.文献[21]基于非单调李雅普诺夫函数方法，提出了两种基于事件的鲁棒采样数据模型预测控制策略.文献[22]利用采样数据信息，研究了一类混合时延复杂网络的事件触发状态估计问题.

需要说明的是，迭代学习控制本质上包含了两个过程，即时间过程和迭代过程，因此利用二维系统理论对迭代学习算法进行分析和设计是一种非常有效的方法.文献[23]将一类线性散系统的ILC设计转化为Roesser模型所描述的二维系统的状态反馈或输出反馈控制问题，利用李雅普诺夫方法得到ILC控制律.文献[24]利用二维分析方法，研究了连续时间迭代学习控制初始状态变化的问题，考虑了两种基于平均算子的PD型ILC算法.文献[25]利用二维Roesser模型，提出了一种由迭代学习控制器和两个当前迭代反馈控制器组成的反馈前馈迭代学习控制方案.因此，本文提出的事件触发机制在二维系统框架下运行，主要研究一类不确定离散系统的迭代学习事件触发鲁棒控制问题.首先，为了节约网络中有限的通信资源，建立了一种事件触发机制，依据触发条件决定控制任务的执行，并且提出了基于事件触发机制的迭代学习控制算法.然后将闭环控制系统转化为典型的二维Roesser模型，利用Lyapunov函数，给出系统渐近稳定的充分条件，最后得到控制器增益的求取方法.仿真结果表明，所提出的事件触发机制在不影响迭代学习算法跟踪性能的前提下，减少了控制网络中控制信号的更新次数，节约了网络资源.

2 问题描述

考虑如下线性离散系统:

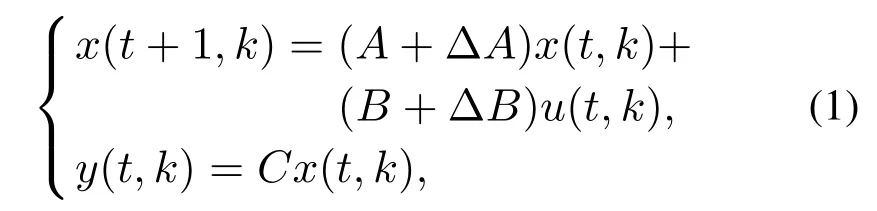
式中:k 代表迭代次数;t 代表时间变量;x(t，k)，u(t，k)，y(t，k)分别为系统状态变量、输入变量和输出变量;A，B，C为具有合适维数的系统参数矩阵.x(0，k)=x0k表示系统在第k次迭代的初始条件.系统在区间t ∈[0，N]上重复运行，且每次运行的期望轨迹均为yd(t).ΔA，ΔB为未知矩阵，代表系统的不确定性，并且满足如下假设[26]:

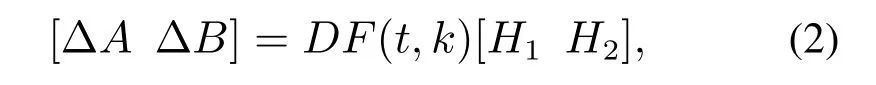
其中:D，H1，H2为具有合适维度的已知矩阵;F(t，k)为具有合适维数的未知矩阵，并且满足F(t，k)T·F(t，k)≤I.

本文考虑如下ILC算法:

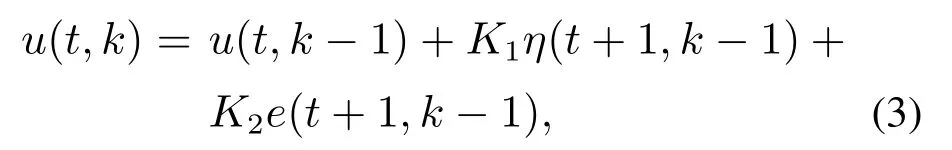
式中:e(t，k)=yd(t)－y(t，k)为系统跟踪误差;η(t，k)=x(t－1，k+1)－x(t－1，k).该控制律由两部分组成:一部分是P型迭代学习控制律，其中输入量随输出误差的比例调整，用于沿迭代周期改进控制量;另一部分是实时状态反馈控制律，用于保证控制性能随时间的变化.

假设上述线性离散系统和ILC算法在网络环境下执行，状态信息和输出信息分别利用单独的通道传输到控制器.为保证系统期望性能的同时节约网络资源，减少控制器更新，在传感器和控制器之间设计事件发生器，采用事件触发机制如图1所示.

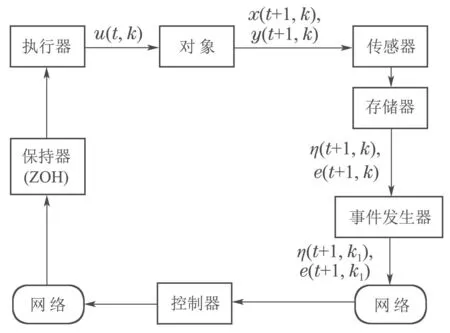
图1 网络控制系统结构框图Fig.1 Networked control system structure

事件发生器用来在每一个采样时刻决定是否将系统数据传送至控制器.本文假设:1)系统所有状态是可测的，并且每次将状态信息和输出信息分别各采用一个数据包传送;2)采样器是时间驱动的，控制器和零阶保持器(zero-order holder，ZOH)为事件驱动的;3)零阶保持器用于当没有最新的控制信号数据包到达执行器时，对控制器输入信号进行保持，即有u(t，k+1)=u(t，k).为方便描述，将η(t+1，k－1)，e(t+1，k－1)扩展为系统新的状态;并将其定义为系统当前采样时刻状态，η(t+1，kl－1)，e(t+1，kl－1)为最新传输至控制器的状态，即系统触发时刻状态，该时刻即为事件触发时刻.其中l=1，2，···，且k1=1.本文的事件触发机制工作如下:传感器在每一个采样时刻对系统信息进行采样并发送至存储器.存储器保存有前两次迭代过程中的系统状态信息x(t，k)、输出信息y(t，k)和扩展状态信息.事件发生器根据提前设定的事件触发条件，提取存储器内所需要的信息对条件进行判断.若系统当前采样时刻状态与系统触发时刻状态满足如下条件(4)，则系统触发时刻状态更新，系统控制器输入u(t，k)更新，当前时刻为最新的事件触发时刻:

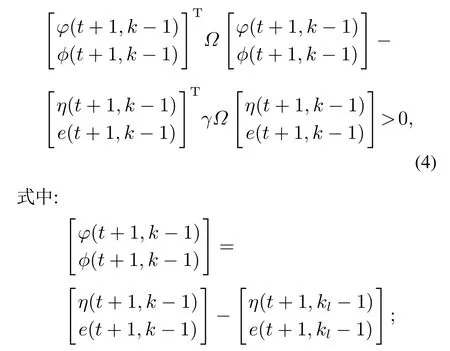
Ω=diag{Ωh，Ωv}是一个正定加权矩阵;γ ∈[0，1)是一个常数标量，代表事件触发参数.

迭代过程中控制器更新过程及触发间隔如图2所示，其中:kl+1表示触发条件第l+1次满足，即控制器进行第l+1次更新;K1，K2为事件触发间隔，代表相邻两次触发时刻之间的迭代次数.且本文假设在第1次迭代过程中，控制器在各时刻都进行第1次更新，即(t，k1)=(t，1).如图2所示，系统在k∈[kl，kl+1)次迭代时，触发条件不满足且控制器保持为上一次迭代的值;在k=kl+1次迭代时，条件判断满足，控制器进行第kl+1次更新.因此根据事件触发条件(4)可知，在下一触发时刻(t，kl+1)来临之前，即k ∈[kl，kl+1)时，系统当前状态与触发时刻状态满足

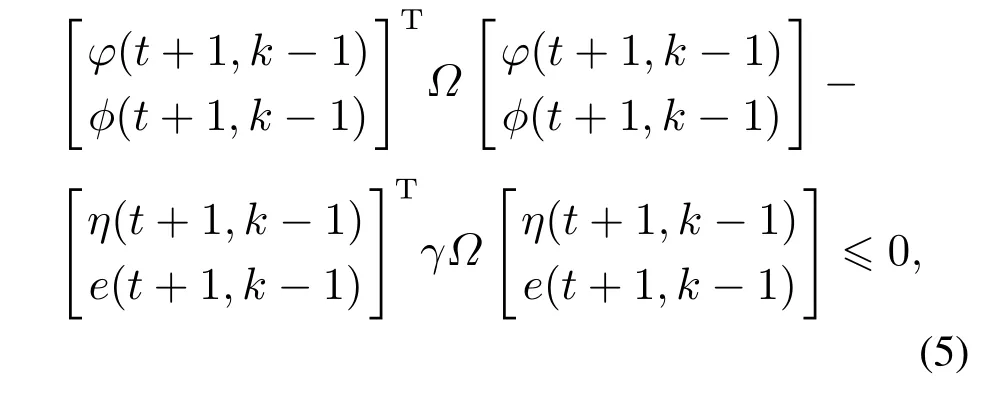
则当前时刻为非事件触发时刻，系统控制器输入不更新，此时控制器输入由零阶保持器保持不变.

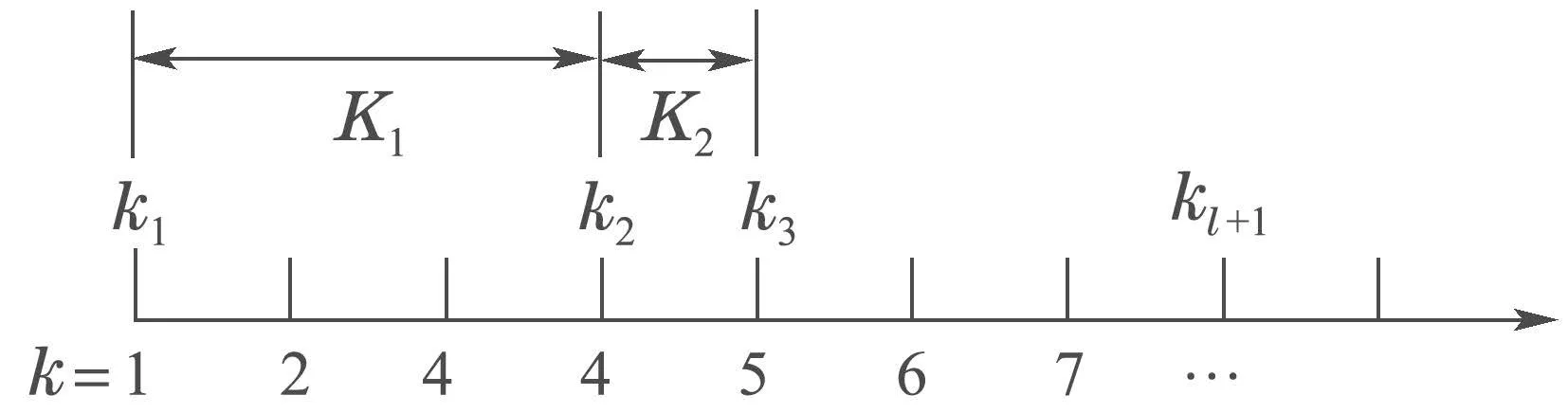
图2 迭代过程控制器更新过程及触发间隔Fig.2 Controller updating process and trigger interval during iterations

因此考虑事件触发机制的ILC算法(3)可描述为

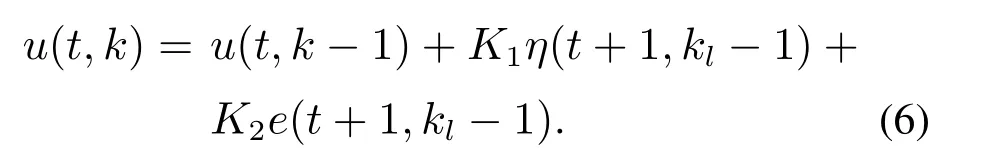
注1在该触发条件下，事件触发时刻为采样时刻的一个子序列.在传感器端，只有一部分采样数据需要被传送到控制器端，较于时间触发机制，降低了通信频率.特别地，当触发参数γ=0时，该机制退化为固定的时间触发机制.

3 主要结果

可以看出，由式(1)和式(6)组成的ILC系统实质上是一个沿时间轴和迭代轴两个方向的2－D系统，因此，可以根据已有的2－D系统理论，建立系统的2－D Roesser模型.

为方便描述，以下定义

由式(1)和式(6)可得

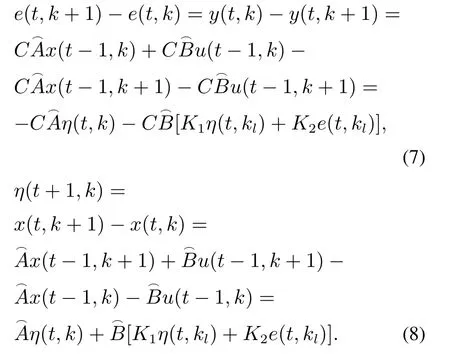
结合式(7)和式(8)，可得

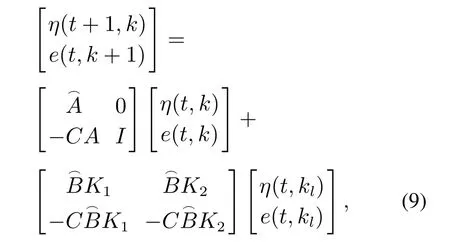
则上式可改写为

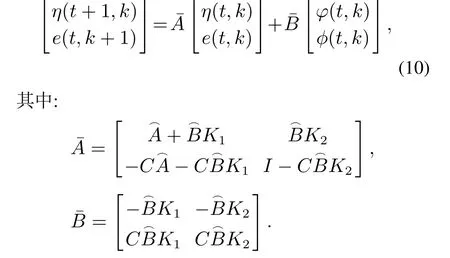
至此将ILC系统(1)和式(6)转化为了一个典型的2－D Roesser系统.可以看出，若2－D系统(10)是稳定的，则ILC系统的跟踪误差是收敛的.本节假设系统矩阵和控制器增益矩阵已知.

下面给出在后续定理证明中需要用到的引理:

引理1(Schur补)对给定的对称矩阵S=，其中S11是r×r维的.以下3个条件是等价的:

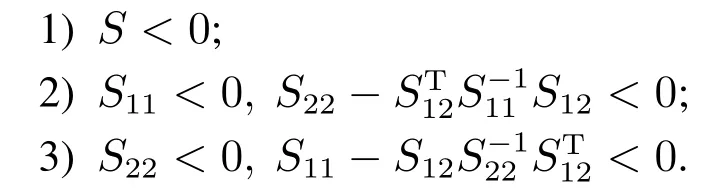
引理2[27]U，V，Ξ和W是给定的具有适当维度的矩阵且W=WT，对于所有ΞTΞ ≤I，不等式W+UΞV +VTΞTUT＜0成立的条件为:当且仅当存在ξ ＞0使得W +ξ-1UUT+ξVTV ＜0成立.

下面定理1给出一个使系统渐近稳定的充分条件，以及系统ILC控制律增益K1，K2的求解方法.

定理1对于2－D线性系统(10)，假设事件触发参数γ和反馈控制增益矩阵K1，K2已知.如果存在正定矩阵P=diag{Ph，Pv}＞0，对称矩阵Ω=diag{Ωh，Ωv}＞0，满足以下条件:

则系统在事件触发机制下是渐近稳定的，其中:

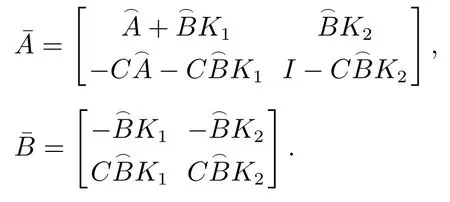
证选取李雅普诺夫函数

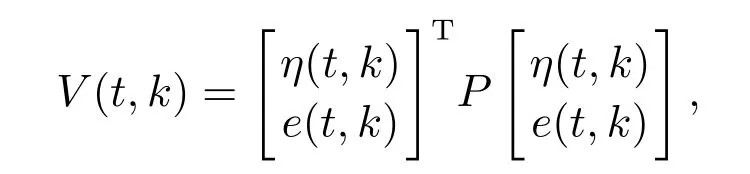
则

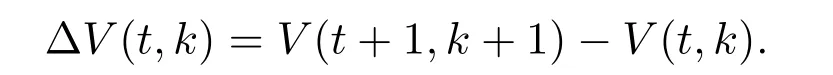
结合事件触发条件(5)可得

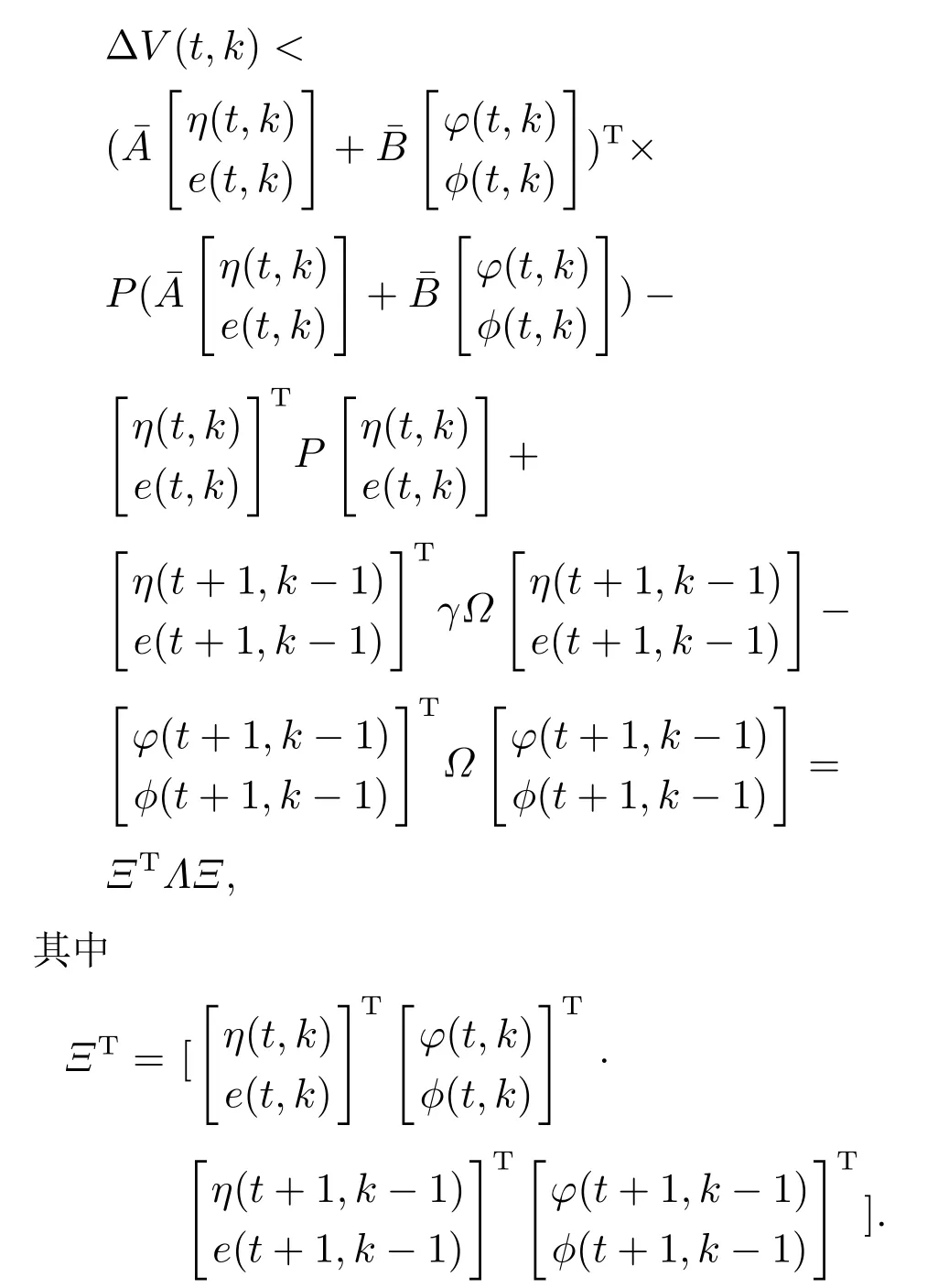
若条件(11)满足，则此时ΔV(t，k)＜0，根据Lyapunov稳定性理论可知带有事件触发的2－D线性系统(10)是渐近稳定的. 证毕.

接下来，利用线性矩阵不等式技术和Schur补引理1，定理1中给出的系统渐近稳定充分条件被转化为一个线性矩阵不等式，并且在定理2中给出了ILC控制律增益的求解方法.

定理2对于2－D线性系统(10)，有事件触发条件(5)，如果存在正定矩阵Xh，Xv和矩阵M1，M2，Ωh，Ωv以及正标量χ满足如下线性矩阵不等式:

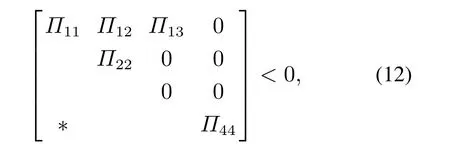
则系统是渐近稳定的，并且存在事件触发控制律增益K1=M1Xh-1，K2=M2Xv-1，其中:

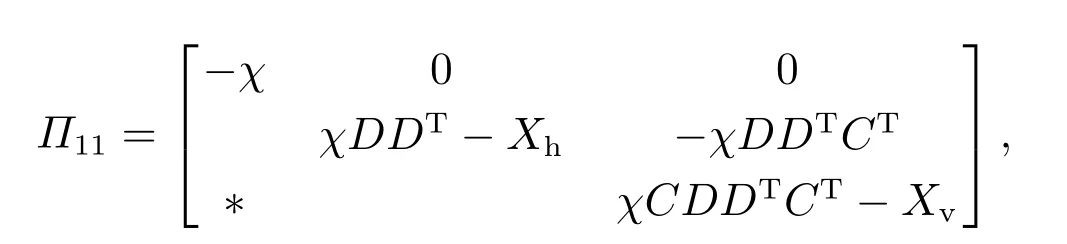
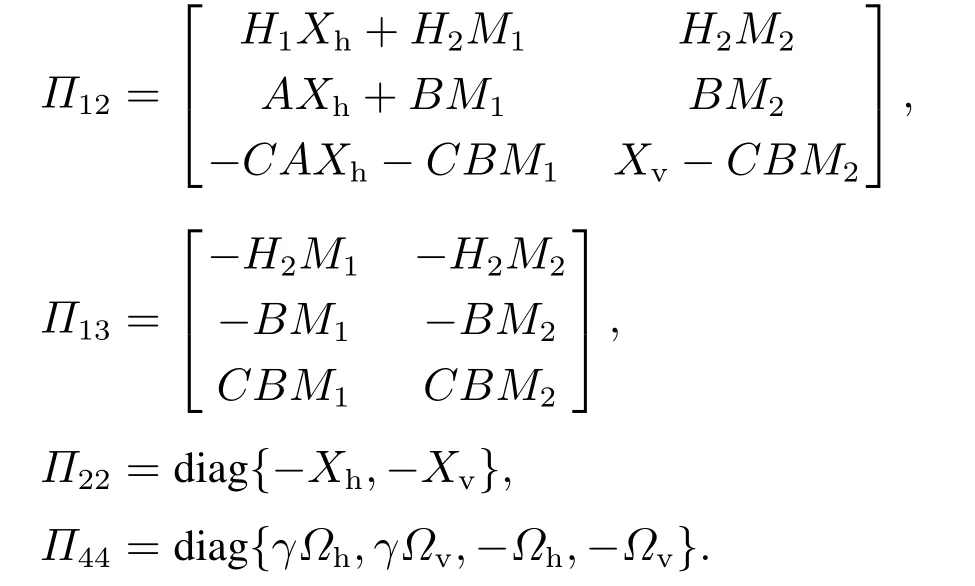
证首先根据定理1可得，已知事件触发参数γ和反馈控制增益矩阵K1，K2，当且仅当矩阵P=diag{Ph，Pv}＞0，Ω=diag{Ωh，Ωv}＞0，使得式(11)成立.

运用引理1，式(11)可转化为如下形式:

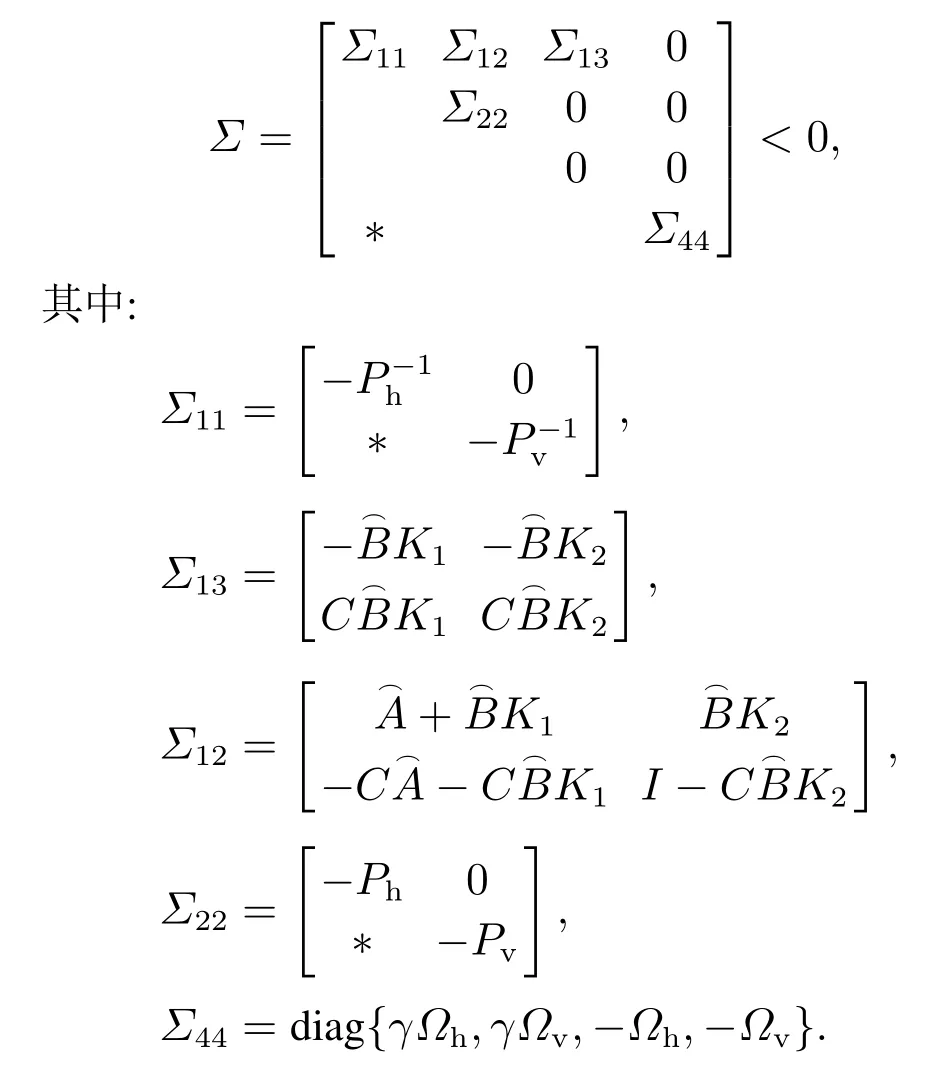
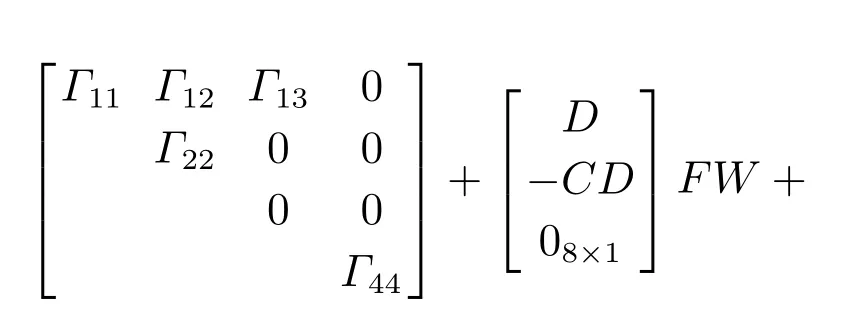
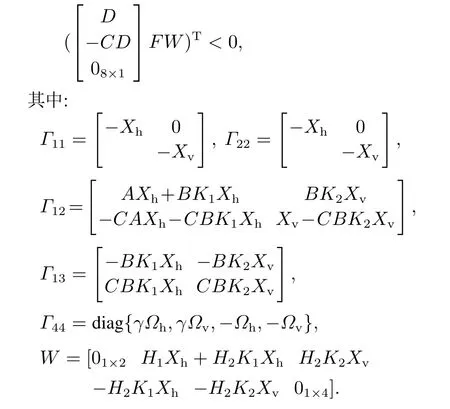
根据引理2，上式对不确定矩阵F(t，k)成立当且仅当存在标量ξ ＞0使得下式成立:

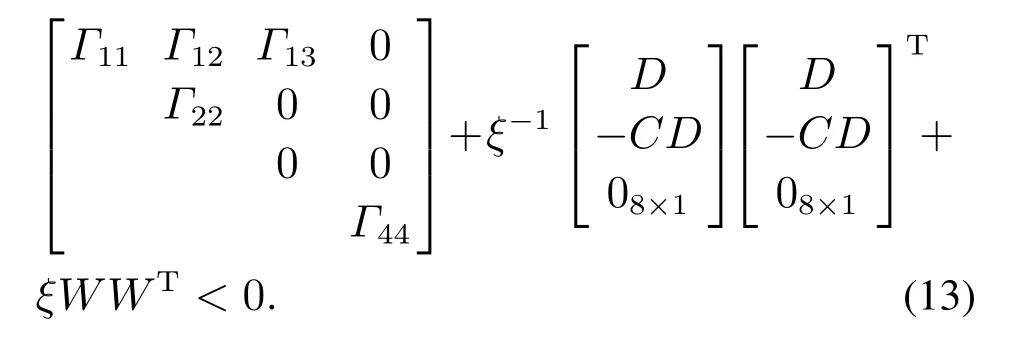
对上式运用Schur 补引理1，并记K1Xh=M1，K2Xv=M2，ξ-1=χ，即可得到线性矩阵不等式(12).式(12)为关于变量χ，Xh，Xv，M1，M2，Ωh，Ωv的一个LMI，可以应用MATLAB中的LMI工具箱进行求解.

证毕.

注2定理1在假设系统参数A，B，C，D，H1，H2和控制器增益K1，K2已知的条件下，给出了系统渐近稳定的一个充分条件.然而在实际系统中，控制器增益K1，K2是未知的，本文的设计任务便是对其进行求解.因此，在定理2中基于定理1给出的充分条件，在系统参数A，B，C，D，H1，H2已知的情况下，将控制器增益的求解问题转化为LMI 是否有可行解的问题.若LMI有可行解，则可求解出系统控制器增益矩阵.

注3二维系统的渐近稳定性是同时沿着两个性能指标方向i，j定义的，其定义见文献[28-29].根据二维系统渐近稳定的定义，定理1和定理2是建立在性能指标t，k同时趋近于无穷的基础上得到的结果，但是迭代学习算法中时间t是有限的.文献[30-31]证明了在时间t有限的约束下，利用上述在t，k趋近于无穷的情况下得到的二维系统理论对迭代学习控制算法进行稳定性分析仍然是有效的.因此，本文在二维系统框架下研究带有事件触发机制的迭代学习控制问题仍然是可行的.

4 仿真示例

本节假设系统(1)的矩阵参数如下:

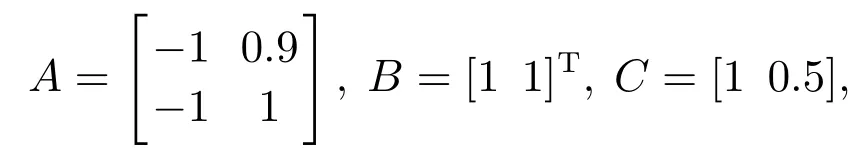
仿真中，ζh和ζv在区间[－0.5 0.5]内随机取值.

考虑如下期望轨迹:

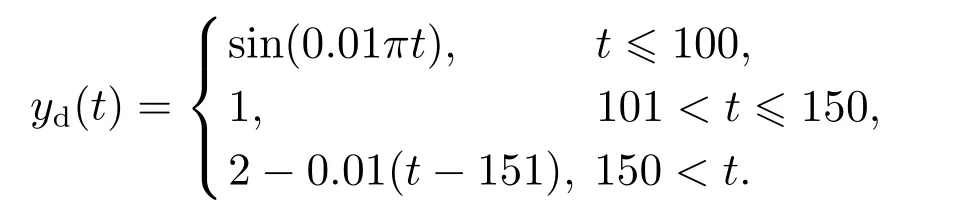
首先考虑在两种不同的触发机制下，系统的最大跟踪误差对比，仿真结果如图3所示.当事件触发参数γ=0时，即系统采用固定时间触发机制时，求解LMI式(13)得到控制律增益为

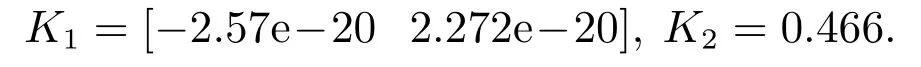
γ=0.8时，得到控制律增益为

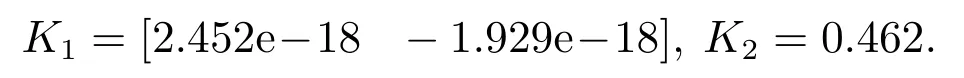
事件触发加权矩阵得

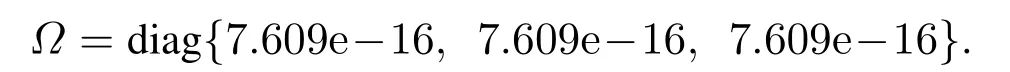
图3 不同触发机制下系统跟踪最大误差对比Fig.3 Comparison of maximum tracking errors under different trigger mechanisms

由图3可以看出在两种触发机制下，系统在经过数次迭代之后，最大跟踪误差趋近于0.在事件触发机制下，系统的最大跟踪误差曲线与固定时间触发误差曲线基本一致，这说明在事件触发机制下系统的跟踪性能并没有因为数据量传输的减少变差.

下面以事件触发参数γ=0.8为例，验证事件触发机制对系统稳定性的影响.系统参数不变，仿真结果如图4－6所示.

其中:图4表示γ=0.8时第4次迭代的系统跟踪效果，图5－6分别表示t=4和150时系统的事件触发间隔.由图4可以看出，在第4次迭代时，系统已基本在整个时间轴内实现期望轨迹的跟踪.由图5－6可以看出，采用事件触发机制较固定的时间触发机制能显著减少数据包传送数量，节约网络资源.特别地，由图6可以看出相邻两次触发时刻之间的触发间隔时间明显增加，此时控制器更新次数由固定触发时间触发的40次降低到15次.这是因为随着迭代次数的增加，系统逐渐实现整个时间轴内最大跟踪误差趋近于0，大幅减少了网络资源的占用.

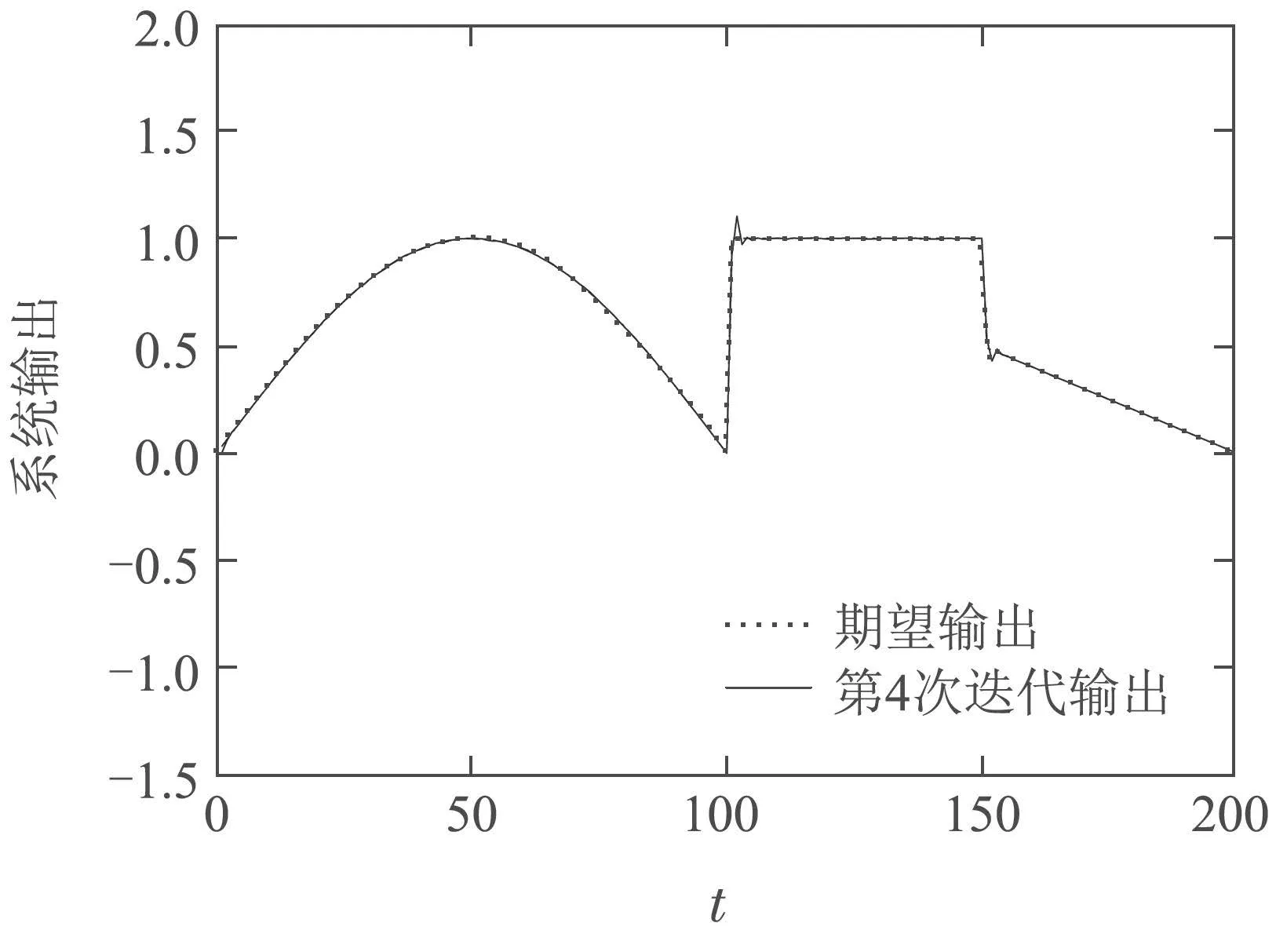
图4 第4次迭代跟踪效果Fig.4 Tracking effects in 4th iteration

图5 时刻t=4系统事件触发间隔Fig.5 System trigger interval for t=4

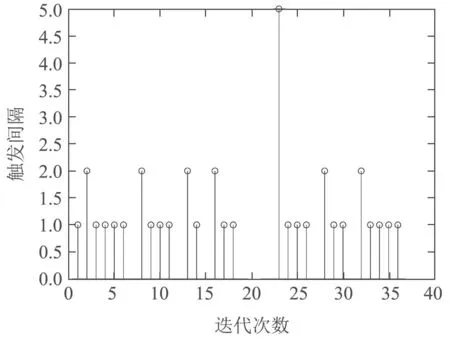
图6 时刻t=150系统事件触发间隔Fig.6 System trigger interval for t=150

接下来进一步研究不同事件触发参数下，系统数据传输量和传输率的变化，仿真结果如图7、表1所示.图7表示事件触发参数γ分别等于0，0.2，0.4，0.6，0.8时，系统迭代过程中的最大跟踪误差.可以看出γ的变化并未对系统的最大跟踪误差曲线造成显著影响;同时由表1分析，数据传输率由100%随触发参数增大大幅减小到50.34%，并且触发参数越大，系统数据传输量和传输率越小.但是，传输率不可能降低至0，因为系统一定需要传输足够的数据才能保持稳定.以上仿真结果表明与固定时间触发机制相比，本文提出的根据系统性能需求、实时状态及其变化量情况决定传输状态的事件触发机制能够在不影响系统稳定性能的基础上，有效减少控制器更新，节约网络资源.

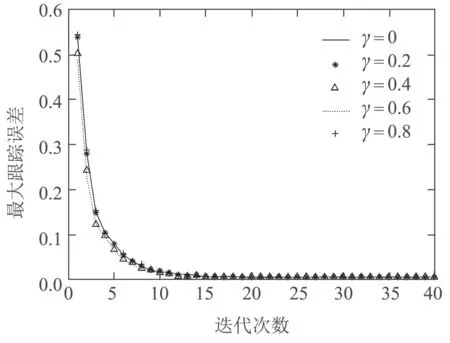
图7 不同触发参数下系统最大跟踪误差Fig.7 Maximum system tracking error under different trigger parameters

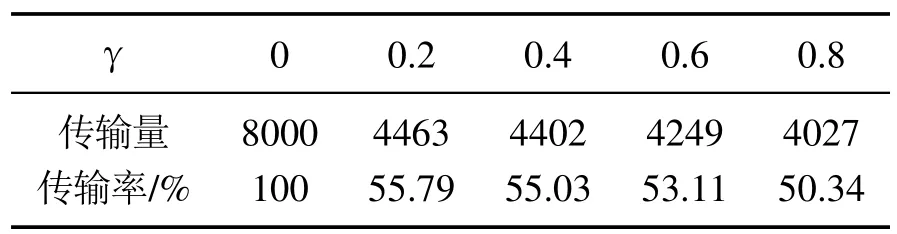
表1 不同触发参数下数据传输量和传输率Table 1 Data transfer volume and rate under different trigger parameters

5 结论

本文在二维系统框架下，针对离散时间线性系统，构造了沿迭代轴的事件触发条件，提出了事件触发机制下的迭代学习鲁棒控制算法.通过引入不确定矩阵考虑了系统的参数不确定性，建立Lyapunov函数推证出了闭环系统渐近稳定的充分条件，并以LMI技术给出兼顾节约网络资源和保证系统性能的鲁棒控制器的求解方法.最后，通过仿真验证了文中提出的事件触发机制能够在不影响系统稳定性能的同时，降低控制器更新频率，减少系统中通信资源的浪费.如何在时间t有限的约束下，进一步降低控制器更新频率，实现二维框架下基于时间轴以及同时基于时间轴和迭代轴两个方向的迭代学习事件触发机制将是笔者以后研究的重点.