基于密度标准误差的局部保持投影故障检测策略
2020-09-05郭青秀冯立伟
张 成,郭青秀,冯立伟,李 元
(沈阳化工大学技术过程故障诊断与安全性研究中心,辽宁沈阳 110142)
1 引言
随着自动化技术的快速发展,通过传感器采集的大量工业数据被应用于不同领域.工业过程数据由于生产系统的规模性与复杂性,通常具有大样本、非线性、多模态、强相关等特征,例如半导体蚀刻过程具有多中心、协方差结构不同等特点.为了获取过程数据的有效信息,基于数据驱动的多元统计过程分析(multivariate statistical process analysis,MSPA)方法被引入工业领域[1-3].
以主元分析(principal component analysis,PCA)为基础的各类算法作为经典的MSPA方法得到广泛应用[4-7].近年来,针对过程数据的不同特征,许多学者提出了PCA的改进算法,如谭等考虑到模态过渡时变量间相关关系的变化,提出了基于差分分段PCA的多模态过程故障监测算法[8].张等通过得分差分以及构建新的监控统计量提出了基于主元分析得分重构差分的故障检测策略,解决了PCA对于多模态过程的监控缺陷[9].但是上述基于PCA的方法在降维时均将数据变化最大的方向作为降维方向,没有考虑到降维后数据的近邻结构是否保持.
为了更好的描述低维空间中数据的结构,流形学习被提出.流形学习假设高维数据可以由低维空间中的流形结构表示且该结构揭示了高维数据的内部信息[10].初期具有代表性的流形学习算法包括基于图框架理论的局部线性嵌入算法(locally linear embedding,LLE)和拉普拉斯特征映射(laplacian eigenmaps,LE)算法[11-12].随后,t-分布随机邻域嵌入(t-distribution stochastic neighbor embedding,t-SNE)被提出[13].LE,LLE以及t-SNE等典型的流形学习算法在人脸识别领域得到广泛发展,但它们均为非线性降维方法,无法处理新的观测数据.因此,He等通过在LE,LLE上引入线性变换提出了局部保持投影算法(locality preserving projections,LPP)和邻域保持嵌入算法(neighborhood preserving embedding,NPE)[14-15].基于流形学习算法的优点,它被专家广泛的应用于各个领域[16-17].故障检测领域中的流形学习算法同样得到快速发展.马等将LLE与支持向量数据描述(support vector data description,SVDD)相结合对化工过程进行有效监控[18].Jia等提出参数t-SNE(parametric t-SNE)方法,在监控较少特征的前提下,该方法能准确识别非高斯、非线性工业过程故障数据[19].Hu等考虑到LPP降维能够保持数据近邻结构的特点,将LPP引入故障检测领域[20].郑等考虑到过程动态性提出了动态稀疏局部保持投影[21].
值得注意的是,上述基于PCA以及LPP算法在对过程进行监控时均使用Hotelling's T2统计量.具有多模态结构的数据不满足T2统计量的假设条件,即假设数据服从多元高斯分布,因此基于PCA以及LPP的算法对多模态过程故障检测有一定的不足[22].
针对多模态过程故障检测,He等提出了k近邻故障检测(k nearest neighbor rule,kNN)算法[23].kNN算法利用样本的前k近邻距离之和作为统计量来判断样本状态,能够有效的识别过程故障.但是,当各个模态的离散程度显著不同且故障发生在密集模态时,kNN算法会出现故障漏报的情况.近年来许多学者对kNN进行改进以提高疏密程度不同的多模态过程故障检测率(fault detection rate,FDR)[24-25].然而上述基于kNN的算法有一个共同的缺陷,即计算量大.通常,除了故障检测的准确性、及时性,计算复杂度同样是评价过程监控方法的重要指标.
针对疏密程度不同的多模态过程故障检测问题,本文提出一种基于密度标准误差的局部保持投影故障检测策略(fault detection strategy based on density standard error associated with locality preserving projections,LPP-DSE).首先,根据截止距离(cutoff distance,dc)确定每个样本的密度与其前k近邻的均值密度;其次,将上述两种密度作差得到密度误差;最后,将样本的密度误差与前k近邻的密度标准差的比值作为新的统计指标,即密度标准误差.当待测样本被判定为故障样本后,本文提出了基于贡献图的密度标准误差诊断策略.本文余下章节安排如下:第2节简要描述LPP算法;第3节详细介绍LPP-DSE故障检测及诊断策略;第4节通过数值例子和半导体工业实例来验证算法的有效性;第5节为结论.
2 局部保持投影
LPP通过寻找投影矩阵A将输入数据Xm×n投影到低维特征空间Ym×l(l ≤n),即Y= XA,m为样本数,n为原始数据变量数,l为特征空间维数.
LPP通过优化下式目标函数求解投影矩阵A:
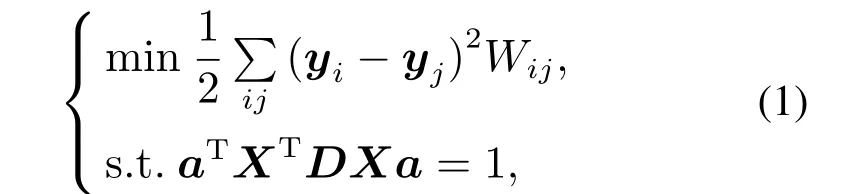
通过简单的代数运算,式(1)可转化为式(2):

其中L= D-W 为拉普拉斯矩阵.通过拉格朗日函数法可将最优化求解问题转化为广义特征值问题,如式(3)所示:

由式(3)求出的前l个最小的特征值所对应的特征向量构成的矩阵即为投影矩阵A,即A=(a1,a2,···,al).
与PCA相同,LPP同样采用T2统计量对特征空间进行监控[20],如式(4)所示:

其中Λ为数据集Y 的协方差矩阵.T2统计了特征空间中样本点到原点的马氏距离,其控制限可由核密度估计法(kernel density estimation,KDE)确定[27].
3 基于密度标准误差的局部保持投影故障检测策略
基于LPP降维可以保持数据局部结构的优点以及过程监控对于降低计算量的需求,LPP被广泛应用于故障检测领域.传统LPP使用T2作为统计指标对特征空间进行故障检测,T2控制限在二维和三维空间分别为椭圆和椭球[22].当变量服从多元高斯分布时,T2控制图可以准确识别故障.当变量具有非线性结构或多模态结构时,T2控制图的故障检测能力明显下降.针对LPP在检测多模态过程时T2统计量的不足,本节提出一种密度标准误差统计量来代替T2对多模态过程进行监控.
假设yi与yj为LPP降维后特征空间的样本点.两点间欧式距离如式(5)所示:

yi的密度如式(6)所示:

其中ρi表示以yi为圆心、以截止距离dc为半径所形成的圆内包含样本点的个数.当yi位于稀疏模态时,ρi较小;当yi位于密集模态时,ρi较大.截止距离dc计算方法如式(7)-(8)所示:

其中Dr-th为D中第r个元素的值,D由步骤①至④求解可得:
①由式(5)得到样本距离矩阵S;
②将S下三角区域元素赋值为0,S上三角区域保留原始数值;
③将S矩阵按行排列得到行向量;
④去除行向量中0元素并升序排列.
num(D)表示集合D中元素的个数;round为四舍五入取整函数;ς为可选参数,由式(6)-(8)可知,ς的取值对ρi具有决定性作用.通过与样本密度交叉验证确定ς的值,当各模态密度差异最大时确定最优的ς.截止距离dc是衡量样本密度的重要参数.dc本质上代表圆的半径,直接决定了样本密度值.当dc较大时,ρi可能出现跨模态情况;当dc较小时,ρi可能为0.密度在一定程度上反应出样本的离散程度.同一模态中样本的密度应位于同一尺度,因此,离散程度不同的多模态过程中样本密度也呈现典型的多模态特征.
定义yi监控指标密度标准误差ρe-i如式(9)所示:

注1由于计算样本前k近邻的密度标准差涉及到参数k,因此k的值经过重复实验选取.k太小导致近邻少,则容易出现近邻密度相同.k 太大会导致近邻跨模态.因此参数k的合理选取可以避免近邻密度标准差为0.
注2当密度误差为0时,代表当前样本密度与其前k近邻样本均值相同,即表示当前样本处于正常样本中,间接验证了当前样本为正常样本.然而密度误差为0会对控制限造成影响,因此需要调整参数k避免该情况.
LPP-DSE故障检测方法共分为两步:离线建模与在线检测.图1为LPP-DSE故障检测流程图.

图1 LPP-DSE故障检测流程图Fig.1 Flow chart of fault detection method using LPP-DSE
1)离线建模.
①利用Z-SCORE标准化对原始数据X进行预处理.
②将预处理后的数据经由LPP投影到特征空间,投影后数据记为Y.
③由式(5)计算Y 的上三角距离矩阵S.
④根据式(7)-(8)确定截止距离dc.
⑤由式(9)计算样本yi的密度标准误差ρe-i.
⑥根据KDE确定控制限ρe-UCL.
2)在线检测.
对于测试样本x*:
①利用离线建模阶段的均值与标准差对x*进行标准化.
②将预处理后的x*经由LPP投影到特征空间,投影后数据记为y*.
③根据式(9)计算y*的密度标准误差.
样本被判定为故障样本后,准确的诊断程序有利于识别异常变量以便保证工序正常运行.接下来对LPP-DSE算法诊断部分进行说明.
由于某些变量的异常变化,故障样本的密度值小于正常样本的密度值,即故障样本偏离正常样本的分布区域.本质上,故障样本与其近邻中心的距离大于正常样本与其近邻中心的距离.
诊断过程包含如下两个部分:特征空间与原始空间.
1)特征空间.
对于特征空间中的样本y,y与其近邻中心m的距离如式(10)所示:

其中ξi=yi-mi(i=1,2,···,l).变量yi对样本y与其近邻中心距离的贡献如式(11)所示:
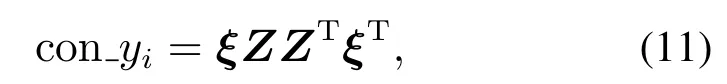
其中Z为l阶零方阵且Z(i,i)=1.
2)原始空间.
假设特征空间中的第i个得分对故障样本与其近邻中心的距离贡献较大,即原始样本x向第i个特征方向投影时对上述距离贡献较大,则样本x的第j个变量对故障样本与其近邻中心的距离贡献如式(12)所示:

根据以上论述,LPP-DSE算法总结如下:
①由于LPP能够在特征空间保持原始数据的近邻结构,因此数据能够被有效投影到特征空间从而降低了过程监控的复杂度.除此之外,LPP降维可以消除数据离群点对模型建立的影响.
②DSE通过密度误差与近邻密度标准差将多模态结构调整为单模态结构,即DSE消除了多模态数据的多中心、离散程度不同等特征,从而提高多模态过程故障检测率.
③待测样本被检测为故障样本后,基于贡献图的诊断策略被提出.通过监控样本各变量对故障的贡献确定故障样本的失控变量.
4 仿真实验
4.1 数值仿真
通过一个数值例子对LPP-DSE进行验证并与其他传统方法进行比较,其具体模型如下:

其中:t与s为驱动变量,模态1中t~U(1,2),模态2中t~U(-11,2),两个模态中s~U(0,10).变换矩阵Φ如式(14)所示:

每个模态各生成400个训练数据用于训练模型.各模态生成10个样本用于校验模型有效性.将模态2中驱动变量t设置为t~U(0.5,0.7),由此生成10个故障样本.并在密集模态生成少量离群点.其数据散点图如图2所示.由图可知,原始数据呈现出典型的疏密程度不同的多模态特征,其中故障由密集模态产生.

图2 数据散点图Fig.2 Scatter plots of samples
接下来利用LPP-DSE对该例进行检测.LPP降维后保留了原始数据的局部结构,如图3所示.
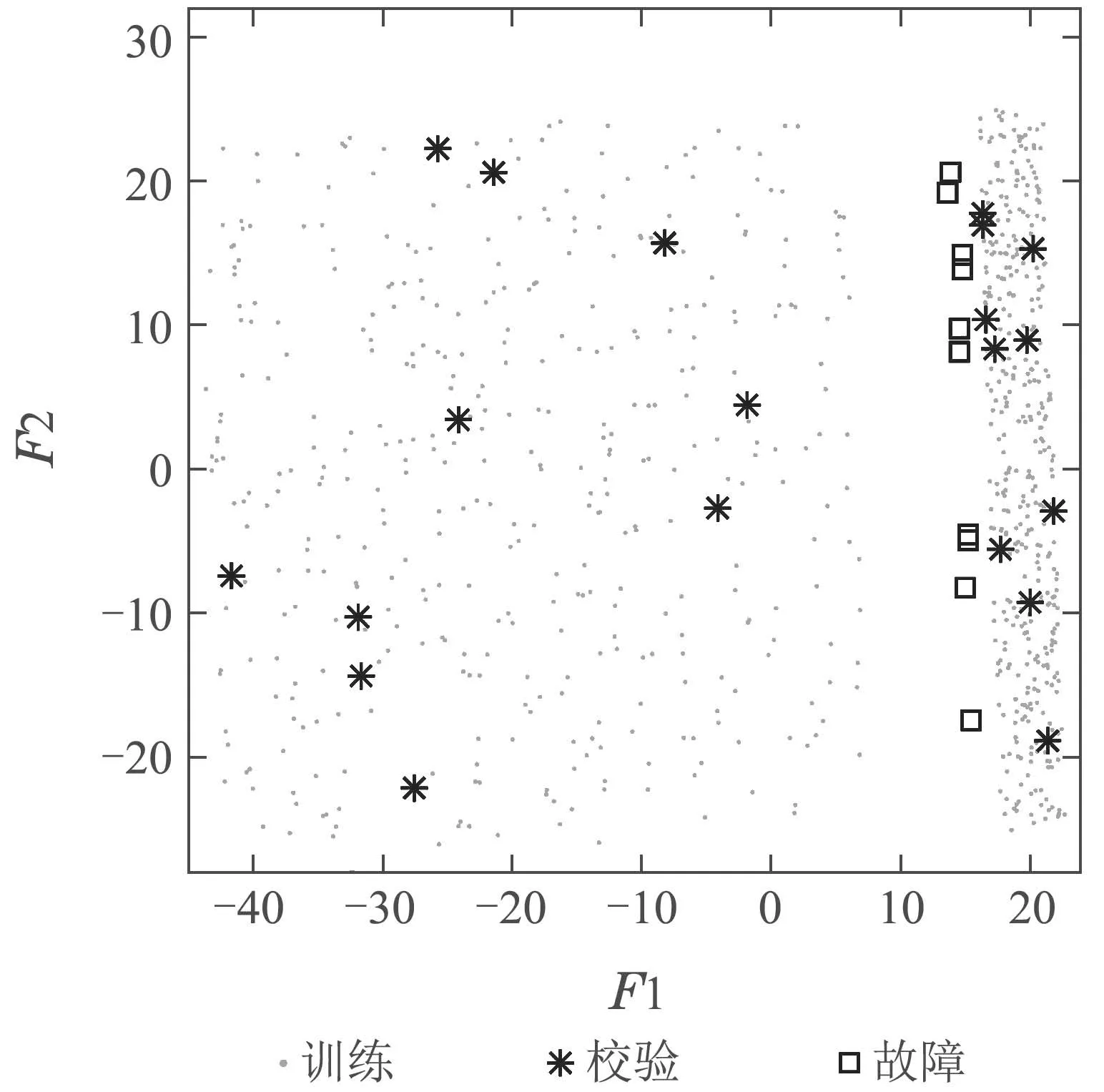
图3 LPP特征空间散点图Fig.3 Scatter plots of samples in FS using LPP
由图可知,LPP在特征空间中保持了原始数据的多模态特征,且故障样本依旧偏离正常样本.此外,LPP还减少了训练数据离群点对模型建立的影响,如图4所示.
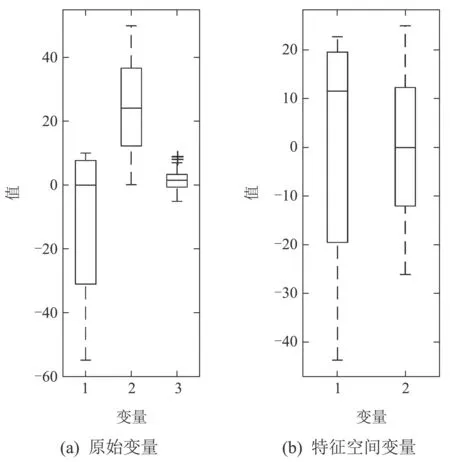
图4 箱线图Fig.4 Boxplots
原始空间中变量3存在少量离群点,而LPP降维后的特征空间中变量无离群点.多模态数据的密度也呈现典型的多模态特征,如图5(a)所示.当密集模态发生小尺度故障时,故障的密度位于两个模态训练数据的密度之间,因此故障难以被分离.通过计算样本的密度标准误差,两个模态样本密度的中心以及离散程度近似相同.由此可见,DSE消除了多模态数据的多中心结构并将不同模态的密度调整到同一尺度,如图5(b)所示.
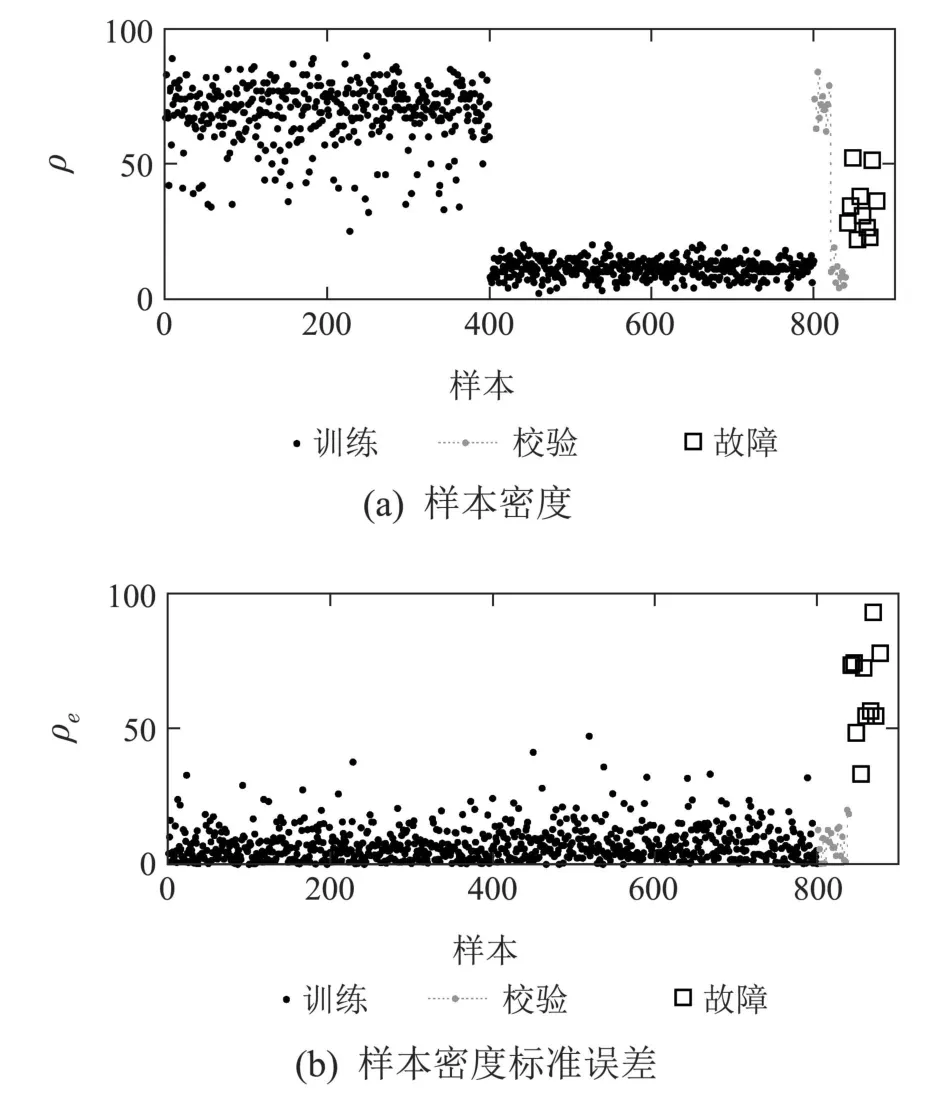
图5 密度分析Fig.5 Density analysis
由于LPP-DSE结合了LPP降维的优势以及DSE能够调整模态结构的特点,因此LPP-DSE检测出全部故障,如图6 所示.为了验证参数k对检测结果的影响,表1列出不同k值对应的FDR.当k太小时,密度误差为0导致控制限制定不合理,因此FDR为0.随着k的逐渐增大,FDR也随之增高.考虑到计算量的问题,当FDR为100%时,最小k值被认为最优,本例为k=11.
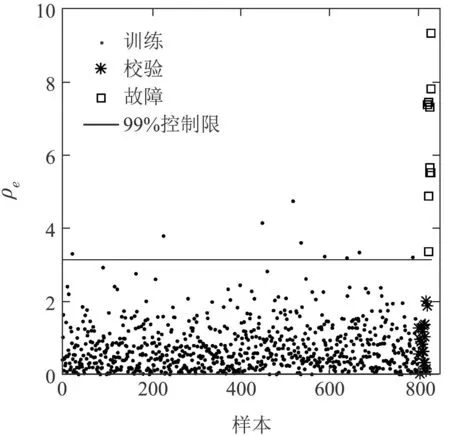
图6 LPP-DSE检测结果Fig.6 Fault detection results using LPP-DSE
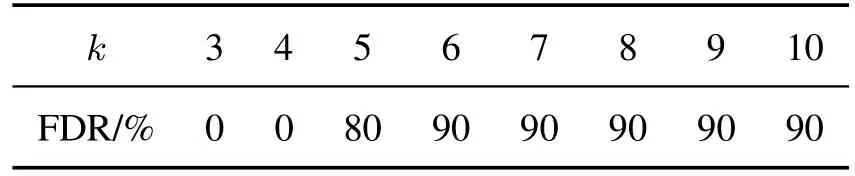
表1 不同k值的故障检测率Table 1 FDR of different k values
为了验证LPP-DSE 的有效性,本节还利用PCA,LPP,NPE,kNN,DSE进行了实验.PCA中主元数根据累计贡献率[28]达到90%确定.各方法参数设置及FDR如表2所示.
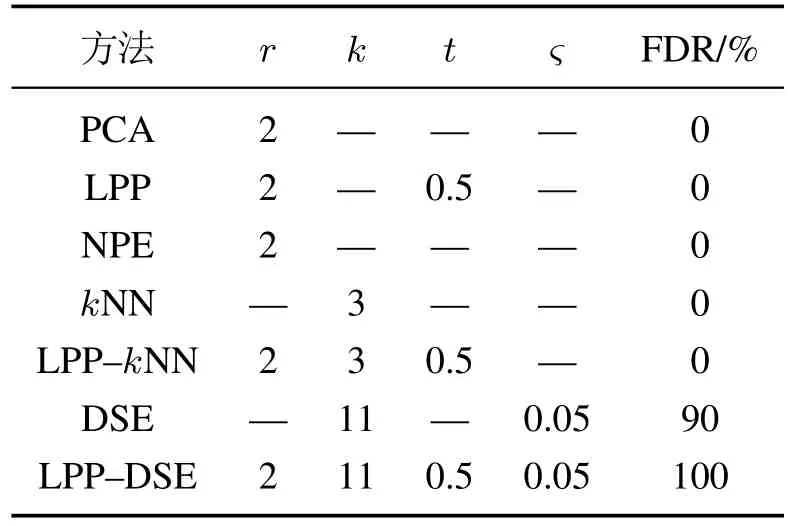
表2 各方法参数确定及故障检测率Table 2 Parameter determination and FDR of methods
PCA,LPP和NPE的FDR均为0.作为典型的线性降维算法,它们可以将数据根据不同规则映射到低维空间.对多模态过程进行监控时,T2被作为监控统计量,而低维空间中的多模态数据不符合统计量的分布假设,因此PCA,LPP和NPE检测故障失效.考虑到数据的多模态特征,kNN被用于测试该例.kNN故障检测率为0的原因是不同模态疏密程度差异较大,控制限完全根据稀疏模态确定,因此密集模态的小尺度故障被检测为正常.LPP-kNN算法虽然降低了检测过程的计算量,但降维后数据模态疏密程度依旧差异较大,因此LPP-kNN检测率为0.针对疏密程度不同的多模态过程,DSE被用来进行检测.DSE利用样本与其近邻的标准误差来判定样本状态为正常还是故障.但当原始数据中变量存在异常值时会影响DSE统计量的稳定性,如图4(a)所示,这会导致控制限确定不合理从而造成故障漏报现象,因此其故障检测率为90%.
根据LPP-DSE对该例的检测结果,本节对已检测出的故障进行诊断,如图7所示.由图7(a)可知,特征空间中的变量1对故障的贡献较大.根据式(11)对异常变量进行回溯,原始空间中的变量1被诊断为异常变量,如图7(b)所示.除此之外,原始空间变量3由0.5t+0.5s构成,当驱动变量t发生偏移时,变量3理应偏离正常区域,然而图7(b)并未诊断出变量3的异常.未诊断出变量3是因为变量3的分布范围远远小于变量1与变量2的分布范围,因此当变量3发生微小偏移时,偏移幅值被变量1的偏移幅值淹没.
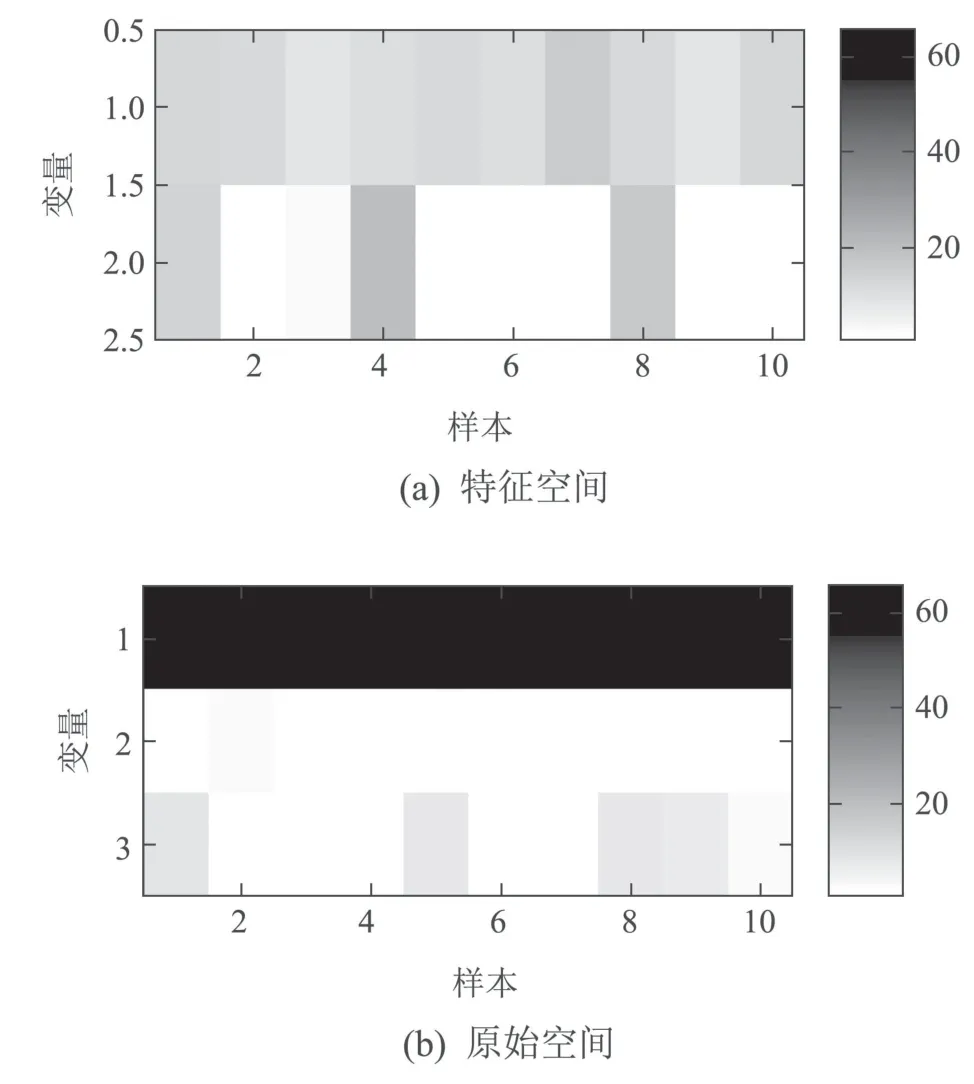
图7 第1类故障的LPP-DSE贡献图Fig.7 Contribution plots of first kind of faults using LPP-DSE
为了验证诊断方法的有效性,将数值例子的故障设置为由驱动变量s的异常变化引起.数据在特征空间的散点图如图8所示,诊断结果如图9所示.
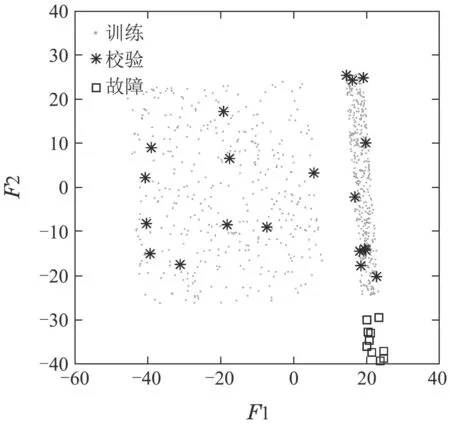
图8 LPP特征空间散点图Fig.8 Scatter plots of samples in FS using LPP
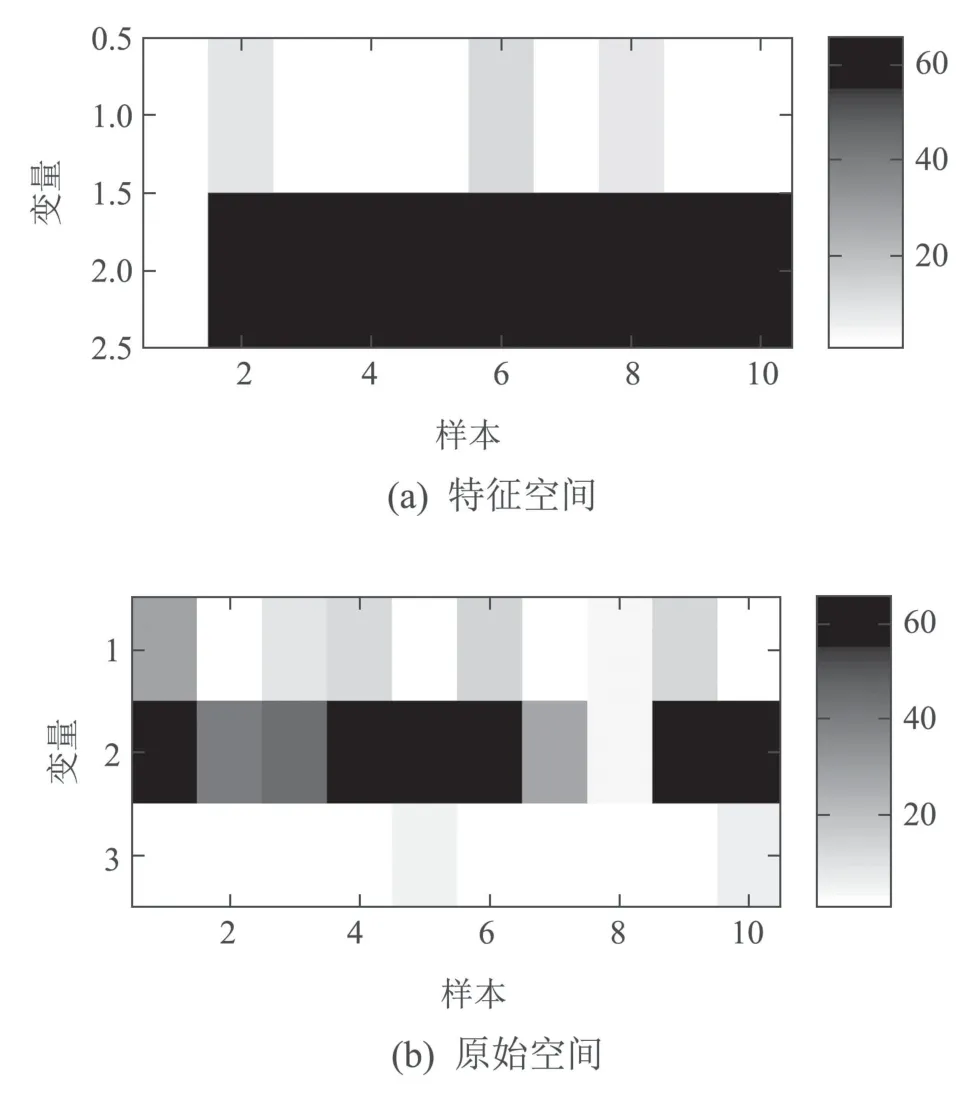
图9 第2类故障的LPP-DSE贡献图Fig.9 Contribution plots of second kind of faults using LPP-DSE
由图9(a)可知,在特征空间中,变量2被诊断为异常变量.由图8可知,特征空间中故障样本的变量2偏离正常区域,两图所反映事实互相吻合.由图9(b)可知,原始空间中的变量2被诊断为异常变量,诊断结果符合故障设置,证明诊断策略有效.
4.2 半导体蚀刻过程
本节数据源自于美国德州的半导体生产中铝蚀刻工艺过程[29].数据集共包含3组实验的108个正常晶片数据与21个故障晶片数据.由于第56个正常晶片存在数据缺失,因此本节只采用107个正常晶片用于建模和校验[3].由于半导体数据为批次数据,因此过程监控前需要将三维数据展开为二维数据.本节利用统计模量分析(statistics pattern analysis,SPA)方法展开数据[30].SPA将每个批次中各变量的均值、方差、偏度与峭度等规则排列为一行作为监控样本.原始半导体数据共有20个变量,通过SPA展开后变量数为80,即过程共包含80个变量.
本节利用PCA,LPP,NPE,kNN,DSE和LPP-DSE对半导体蚀刻过程进行监控,各方法参数设置如表3所示.

表3 各方法参数确定Table 3 Parameter determination of methods
由于PCA,LPP和NPE均利用T2作为统计量,因此半导体数据的多中心特征导致这类方法未能检测出全部故障,检测率如表4所示.由于半导体过程中3个模态的中心与疏密程度不同,如图10所示,因此kNN检测率仅为38.1%.DSE虽然融合了半导体过程的多中心结构,但对于训练样本的边缘点较为敏感,导致控制限被边缘点影响,因此DSE检测率为33.3%.LPP-DSE检测结果如图11所示.LPP将原始80维数据投影到34维特征空间,在保持数据局部结构的前提下不仅降低了计算复杂度,还降低了离群点的影响.DSE通过密度标准误差将3个模态融合为疏密程度近似相同的单模态结构,从而成功检测出21个故障,如图11和表4所示.

图10 变量3的均值与方差散点图Fig.10 Mean and variance scatter plot of variable 3

图11 LPP-DSE检测结果Fig.11 Fault detection results using LPP-DSE

表4 故障检测率Table 4 Fault detection rate
接下来,本节对检测出的故障进行诊断分析.以故障1为例,特征空间中故障1的变量2对统计值的贡献最大,如图12所示.

图12 故障1的特征空间贡献图Fig.12 Contribution plots of fault 1 in feature space
图13为原始空间中变量对统计值的贡献,由图13以及SPA展开时变量的排列可知,故障1中变量13对统计值ρe的贡献最大.根据文献[30]可知,故障1的类型为TCP+50,变量13对应TCP impedance.
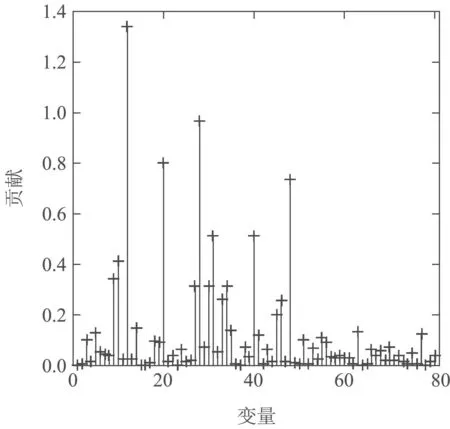
图13 故障1的原始空间贡献图Fig.13 Contribution plots of fault 1 in raw space
图14为训练数据与故障数据变量13轨迹图,进一步验证了故障样本的变量13发生偏移,从而证实了诊断策略的有效性.故障2与故障3的诊断结果分别在图15与图16给出.由诊断结果分析可知,故障2与故障3分别由变量12(RF impedance)与变量11(RF power)异常变化引起,符合故障设置[30].

图14 变量13轨迹图Fig.14 Trajectory plot of variable 13

图15 故障2的原始空间贡献图Fig.15 Contribution plots of fault 2 in raw space
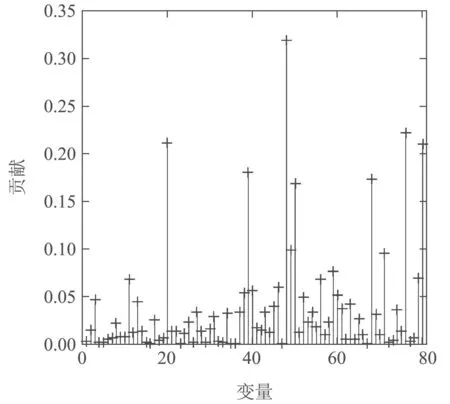
图16 故障3的原始空间贡献图Fig.16 Contribution plots of fault 3 in raw space
5 结论
本文提出了一种基于密度标准误差的局部保持投影故障检测策略以提高多模态过程的故障检测率.该方法既继承了LPP降维后保持数据结构的优点,又降低了过程监控的复杂度;DSE通过计算降维后样本的密度标准误差将各模态的离散程度调整到同一尺度.通过仿真实验以及结果分析验证了LPP-DSE的有效性.
由于本文中参数ς对于样本的密度影响较大,因此下一步研究方向为减少参数ς对于检测结果的影响.
