教育数学观下的解题探索*

刘家琪 胡 康

(江苏省扬州大学数学科学学院,225002)

在基础教育课程改革中,教育数学关注数学学科内容改革,致力于对数学学科材料进行改造、创新优化,揭示各类数学知识之间的紧密联系,发现数学规律形成的优化过程,选择最优呈现形式.作为新的数学教育观的反映,教育数学也发掘普适性解决数学问题的方法,让学生轻松地学习数学知识的同时,掌握数学本质,培养数学能力,提高数学学科素养.本文通过具体例子,从改变呈现方式、灵活切换处理和寻求本质等几个方面阐述教育数学观下的数学解题[1].

一、改变呈现方式

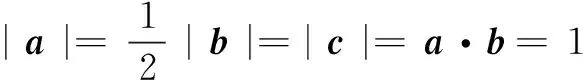
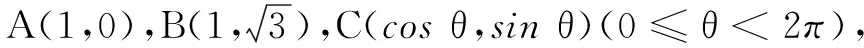
思考新教育数学观提倡重新思维[1].求模长问题并不一定非要通过坐标解法,有时数形结合解题更为简便,可以省去大量繁琐的计算及技巧性较高的代数式转化.此题目标式前后两个模长的系数不一致,我们可以改变问题的呈现方式,结合圆的条件,利用阿波罗尼斯圆的性质,通过改变向量达到调整模长系数的效果,从而将问题转化为模长一致的情况,最终构造出理想的几何模型进行求解.

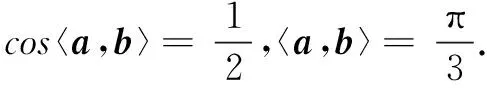
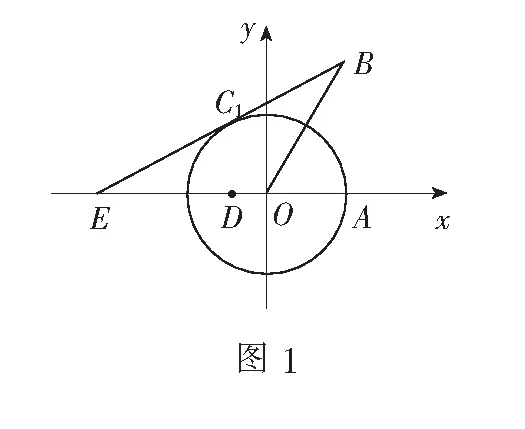
如图1,由两点间直线段最短,知B,C,E

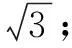
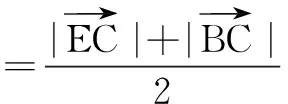
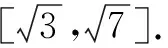
二、灵活切换处理

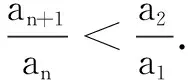
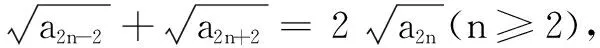
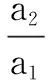
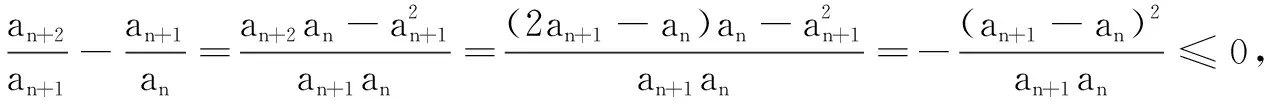
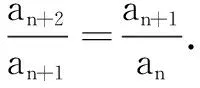
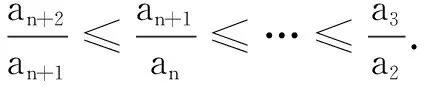
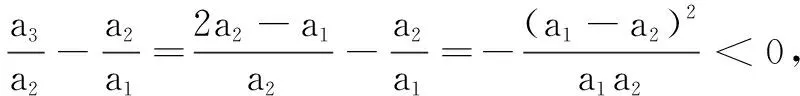
三、寻求本质

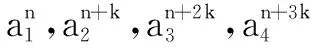
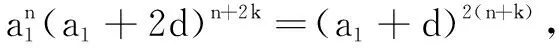
4ln(1+3t)ln(1+t)

=ln(1+3t)ln(1+2t)

+3ln(1+2t)ln(1+t).

(*)

由此作差构造函数,将等式问题转化为函数零点问题,经过复杂计算和四次求导得方程(*)只有唯一解t=0,从而假设不成立,即不存在a1,d及正整数n,k符合题设.

思考本题参数较多,用函数观点考虑数列问题时,可抓住等差数列{am}的通项公式为项数m的一次函数这一本质,以m为自变量将等式问题转化为函数问题,避免常规方法繁杂的计算,通过一次求导就能分析出函数的单调区间,轻松找出矛盾所在[2].

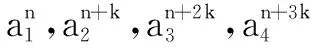
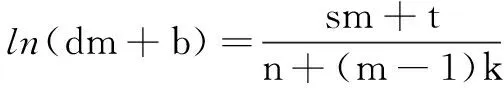
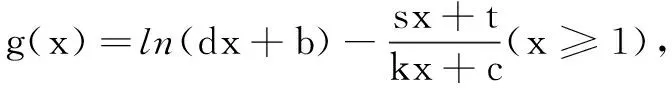
综上,不存在a1,d及正整数n,k满足题设条件.

教育数学侧重于优化改造数学素材本身,使其更适合于数学学习.在数学解题领域,数学教育注重技巧,思维高度,知识广度;而教育数学希望有普适性解决问题的方法,力争低起点、适量知识,但能抓住本质,同时避免繁杂的计算.以上几个案例的分析,让我们初步领略到教育数学视角下解题的优势.