在变式训练中提升学生的思维能力——以一道最值问题的教学为例

李富国

(江苏省苏州丝绸中等专业学校，215228)

一、问题背景

数学思维的训练和能力的提高离不开解题,解题是学生掌握数学知识的主要途径,也是检验学生理解知识,运用知识的有效形式.在课堂教学中,经常碰到一些形式简单、知识点丰富、解答方法灵活的问题,对促进学生思维发展、提高解题能力大有裨益,具备较高的研究价值,值得我们进行教学反思.笔者对一道课堂上引起师生共鸣的最值问题加以剖析,希望抛砖引玉.

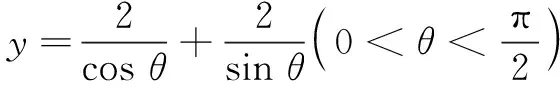
本题结构简单,形式对称,学生利用基本不等式很快得出了正确答案.

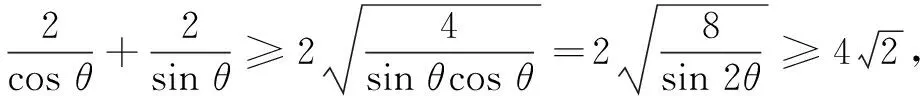
为了进一步提升学生的思维能力,培养思维的严谨性,使学生明确用不等式求最值时,不等式中的等号需能成立,笔者设置了如下变式题.

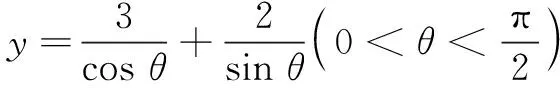
设计意图打破原题型的对称性表征,从结构上对函数表达式进行改造,将问题引向深入,有利于克服学生解题过程中的机械性模仿,活跃学生思维形式与观察问题的角度,有效提升学生的数学抽象、逻辑推理等核心素养.

二、思维碰撞

果不其然,学生在例1解法的“示范”作用下,由基本不等式出发展开思路,在错解中不断修正逻辑缺陷,在思维碰撞的火花中走出困境,最终成功得到了答案.通过这种具有强烈对比性、相似性、差异性的问题,对挖掘学生思维的深刻性和延伸学生思维广阔性有着无比优越的好处.

问题给出后,首先有学生给出如下解答.

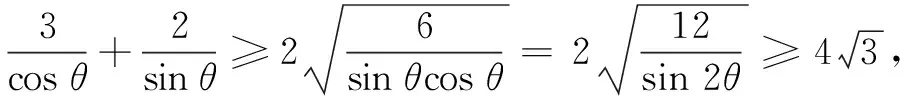
很快,有其他同学质疑.

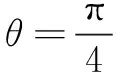
师:相同的方法竟无法确定正确答案,如何改进?

(此时的教学情境使学生陷入了不愤不启与不悱不发的氛围.笔者的提问,也使学生的大脑思维机器处于高速运转中.)

很快,有学生提供了新的解题思路.

至此,问题似乎得到了完美的解决,无懈可击!突然,有学生提出不同意见.

师: (笑问)为什么?

设计意图学生验算推理的过程,实际上是观察与归纳总结的过程.推理的缩短、方法的改变,有利于学生概括和思维能力的提高,培养学生思维的敏捷性和批判性.

正当大家感觉很失望到时候,笔者加以思维引导.

师:由不等式入手,看来有些困难重重!(进一步追问)求函数的最值,除了不等式法,还有什么方法?

经笔者点拨,学生达成共识,如果将y看成θ的函数,用函数的思想和方法解答可使问题完美解决,形成了如下解答.

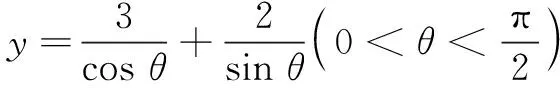
设计意图在解决一类复杂和抽象函数问题时,若使用常规的初等数学方法无法解决问题,导数思想和方法经常可以发挥非常大的作用.在解决问题遇到困境时,改变观察问题的角度,可以锻炼学生的转化与化归思想的运用,培养思维的深刻性.

三、拓展提升

此时,趁着学生思考的热度,可以帮助学生延续思维的发散性,拓宽学生的知识面,更好地解决实际问题.

师:回顾上述解题过程,变式题在用不等式法解题时之所以遇到困难,其主要原因是例1的函数表达式中分子的对称性被打破,导致对后续解题过程产生较大影响.要消除这种差异,回归平衡状态,我们可以借用不等式理论中另一个著名的不等式——权方和不等式.

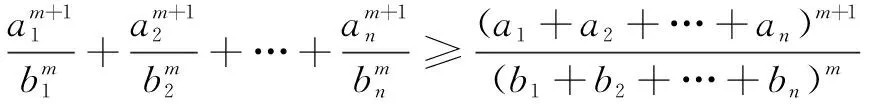
(此结论的相关证明过程可鼓励学生课后通过网上阅读、查资料等方式进行学习)

师:借助权方和不等式,变式题该如何解答?

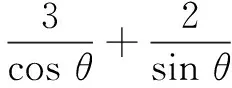
众生:这真是妙解!

(课堂沉浸在一篇喜悦气氛中)

设计意图常言道:学无止境.数学知识的学习和数学思维能力的发展,不能仅仅满足于课堂,需要延伸的社会,伴随人的一生不断成长.延伸课本知识,激励学生课外拓展,体现了教育的人格培养功能.

四、课后反思

纵观上述教学,四种解法从不同的思维角度,利用不同的数学知识与方法得到了不同的探索.解法3和解法4得到了正确的答案,而解法1和解法2却得到错误结果,错误的结果并不可怕,可贵的是在这先后的解题探讨过程中,学生的思维一直在不停地运转,从基本公式的运用,基本方法的选择,到最后解题结果的自我反思.在高境界的课堂教学过程中,学生一定积极思考,虽然思维往往有一定局限性,但学生创造性的思维火花却经常出现,即使是一些片面的、不成熟的,甚至是不正确的思想,教师都要及时捕捉并加以启发引导.本节课学生的思维始终处于一波未平,一波又起的过程中,这种跌宕起伏的课堂氛围,始终在为学生创造一个宽松适合的学习氛围.相信广大教师若能持之以恒,学生的思维能力和数学素养一定可以得到有效提升!