巧用向量化解几何体中点的坐标表示问题

吴志鹏 陈玉兰

(福建省德化第一中学，362500)

通过建立空间直角坐标系,把空间几何体中的点用坐标表示,进而利用空间中直线的方向向量、平面的法向量进行求角或求距离的运算,这是利用空间向量进行解题的思路.但近年来一些立体几何问题中,在表示点的坐标时,有些点不能直接观察获知,即出现难以用坐标表示的“难”点,增加了问题求解难度. 如何突破此类难关,本文总结求点坐标的一些方法,供读者参考.

一、定点问题

1. 确定不能直接标记坐标的点

例1如图1,在三棱柱ABC-A1B1C1中,BC=BB1,BC1∩B1C=O,AO⊥ 面BB1C1C.

(1)求证:AB⊥B1C;

(2)若∠B1BC=60°,直线A1B1与平面BB1C1C所成的角为30°,求二面角A1-B1C1-B的余弦值.

解(1)因为AO⊥平面BB1C1C,所以AO⊥B1C;因为BC=BB1,所以四边形BB1C1C是菱形,BC1⊥B1C.又AO∩BC1=O,所以B1C⊥平面ABC1,从而B1C⊥AB.

(2)因为A1B1与平面BB1C1C所成的角为30°,A1B1∥AB,所以AB与平面BB1C1C所成的角为30°.因为AO⊥平面BB1C1C,所以AB与平面BB1C1C所成的角为∠ABO=30°.

评注建立坐标系后,点A1的坐标不能直接进行标记,此时利用向量的三角形法则运算、向量共线、向量相等等运算,轻松获得点A1的坐标,解决问题.当然,也可以通过棱柱的两底面平行,用面ABC的法向量替换面A1B1C1的法向量进行计算.

2. 确定不能标记位置点的坐标

评注本题球心坐标很难直接进行标记,此时假设球心O(x,y,z)，建立关于x,y,z的方程组,变几何问题为代数问题,这也是在空间几何体中求点坐标常用的一种方法.

二、动点问题

动点问题是空间中求点的坐标的一个难点.由于动点的坐标要满足一定的约束条件,有必要先求出动点的轨迹方程,再根据其方程假设出动点的坐标,并利用向量共线、模相等、夹角关系等获得动点的坐标.

1.动点在某坐标面内与坐标轴垂直的直线上

例3如图3,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥面ABCD,PA=AB,E为线段PB的中点,F为线段BC上的动点.

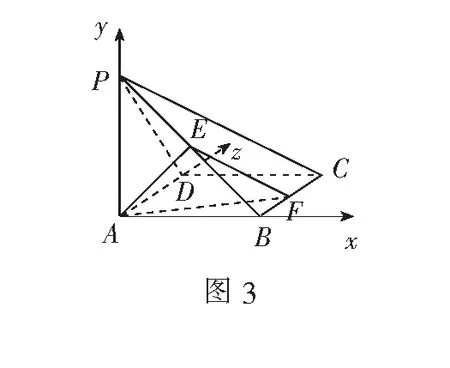
(1)求证:平面AEF⊥平面PBC.

(2)试确定点F的位置,使平面AEF与平面PCD所成的锐二面角为30°.

解(1)略.

故当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30°.

评注利用点F在坐标面xAy上,且BC⊥AB,设点F的坐标时只需引入单参数,降低问题求解难度.

2. 动点在某坐标面内的直线上

(1)证明:平面PAC⊥平面ABC;

解(1)略.

3.动点在空间结构中的直线上

例5在∆ABC中,AB=BC=2，∠ABC=90°，点E,F分别为AB，AC的中点,将∆AEF沿EF折起,使点A到达点P的位置,且PB=BE，如图6所示.

(1)证明:EF⊥平面PBE；

(2)设N为线段PF上的动点,求直线BN与平面PCF所成角的正弦值的最大值.

解(1)略.

(2) 由(1)知EF⊥面PBE,进而面PBE⊥面BCFE.取BE的中点为O,由PB=PE,可知PO⊥BE，所以PO⊥平面BCFE.

设BN与面PCF所成角为θ,则

评析动点N在线段PF上,但此时线段PF所在的直线并不在某一个坐标平面中,利用向量共线关系可方便地将动点N的坐标用参数λ表示,使问题求解得以顺利进行.