高速列车作用下季节性冻土区桥墩及周围场地的动力响应

郑海忠 严武建，2 石玉成，2 卢育霞，2 王平，2 李福秀

（1.中国地震局兰州地震研究所中国地震局（甘肃省）黄土地震工程重点实验室，兰州 730000；2.甘肃省岩土防灾工程技术研究中心，兰州 730000）

随着列车速度和载重的大幅提高，铁路沿线的振动问题更加突出。特别是在季节性冻土区，由于长期的冻融循环作用，铁路路基发生变性破坏，影响列车的运行安全。列车荷载作用下，地面振动特性的研究主要集中在现场实测分析和数值模拟计算2方面。夏禾等［1］对铁路桥梁以及铁路附近地面和建筑物的动力响应进行了2 次现场测试，发现地面和建筑物的振动随着列车速度的增加而增大，距离线路越远地面和建筑物的振动越小，但在距线路一定范围内有一个振动放大区。高广运等［2］分析了秦沈铁路沿线不同列车编组和速度对地面振动的影响。陈建国等［3-4］对京广铁路某区段附近列车引起的地面振动进行现场测试，分析地面振动的特点及衰减规律。王子玉等［5］对季节性冻土区铁路路基振动加速度进行现场监测和振动分析，发现冬季土体冻结，其刚度和强度增大而阻尼比减小，振动衰减缓慢；春融季由于土体含有大量的水分，甚至处于饱和状态，土体强度减弱，加速度峰值在纵向和竖向减弱，水平方向稍有增强。董连成等［6］对多年冻土区列车荷载作用下的动力响应进行分析，对比客车和货车运行引起的路基振动特性。吴志坚等［7-8］对列车荷载作用下多年冻土区的振动特性和土体蠕变特性进行研究，发现列车振动从路基中传播会发生大幅度的衰减；在重复列车荷载作用下土体发生蠕变，且在列车运行的第1年沉降最大，随着时间的增加蠕变基本保持不变。刘维宁等［9］建立了列车-轨道-衬砌结构-地层系统的三维有限元模型，研究地铁列车引起地面振动的传播规律。翟婉明等［10］采用有限单元法结合车辆-轨道耦合动力学，建立列车-轨道-土体三维有限元分析模型。Hung等［11-12］建立地铁运行引起土体振动的2.5D 有限元-无限元模型，并考虑轨道不平顺动力特性。

目前，对列车荷载作用引起的振动传播特性的研究主要集中在路基和地面，且都是针对同一场地，而对桥墩和不同基础场地的振动传播特性研究较少，季节性冻土区桥墩在不同基础场地的研究更是鲜有涉及。冻土场地具有冻胀性和融沉性，与常规场地存在明显差别。

本文选取哈大高速铁路沿线桥墩及周围不同场地为研究对象进行现场振动测试，利用ABAQUS 有限元软件分析场地弹性模量和几何参数变化对振动传播的影响。

1 现场测试概况

哈大高速铁路线路全长921 km，是我国目前在最北端的季节性冻土地区设计建设标准最高的一条高速铁路，全线采用无砟轨道，最高速度目标值是350 km/h。选取哈大高铁沿线铁岭—四平段桥墩及周围不同场地进行现场测试，该测区冬季极其严寒，最大冻结深度可达2 m 左右，土质为冻胀敏感性土。测试仪器采用中国地震局工程力学研究所研制的891-Ⅱ型测振仪，该仪器的加速度测试范围为0～2.0g。在本次测试中规定水平向x分量为列车运行的方向，水平向y分量垂直于铁路线，垂直向z分量为重力方向。

为了研究桥墩及周围不同场地的振动特性，共布置了3个测点（图1）：1#测点布置在桥墩左侧的基础场地上，距桥墩底端水平距离0.5 m；2#测点布置在桥墩顶端支座垫石上；3#测点布置在桥墩右侧堆积填土上，距桥墩水平距离0.1 m；堆积填土高1.8 m，长3 m。

图1 测点布置（单位：m）

2 加速度信号时域分析

CRH2C型列车通过时不同测点z方向加速度时程曲线见图2。可见：①1#测点和3#测点的振动方向（正向和负向）基本无对称性，且3#测点正向的加速度峰值与负向峰值相差较大；2#测点的振动方向有很好的对称性，正负向的加速度峰值基本相等。②1#—3#测点的加速度峰值分别为33.5，23.1，64.6 cm/s2，1#测点和3#测点比 2#测点分别放大了 1.45，2.80 倍，说明在列车荷载作用下，场地对振动有放大作用，不同场地对振动的放大特性不同。③列车经过时振动有8个明显的周期性峰值（图2（b）），主要是列车轮对周期性经过产生的，且该列车由8 节车厢组成。相邻2 个峰值出现的时间间隔大约为0.3 s，而我国高速铁路的车厢长度为25.5 m，推算列车运行速度约为85 m/s。

3 加速度信号的EMD分解与频域分析

3.1 EMD分解

图2 不同测点z方向加速度时程曲线

Huang 等［13］深入研究了瞬时频率的相关理论，创造性地提出了固有模态函数（intrinsic mode function，IMF）的概念和经验模态分解（EMD）法，建立时频分析的新方法——Hilbert-Huang Transformation（HHT）。该方法指出，任意信号x（t）都可分解为有限个固有模态信号（intrinsic mode signal，IMS）或固有模态函数IMFi（t）和残余函数r（t），其表达式为

在列车经过时对桥墩左侧基础场地1#测点的加速度响应信号进行EMD 分解，见图3。可见，随着IMF阶数的增加，振动信号的频率和振幅越来越小。

3.2 信号滤波处理

由于周围其他环境激励的影响，难免会混入一些不必要的振动，使得现场所测振动加速度数据不能直接使用，需要进行滤波处理，而周围环境激励引起的振动以低频振动为主［14］。因此，本文利用EMD分解并结合相关性分析对测试数据进行滤波处理。

EMD 可以将原始数据按照频率由高到低的次序分解成有限个IMFj，对每一阶IMFj与n个原始数据x进行相关性分析求出其相关系数，其数学表达式为

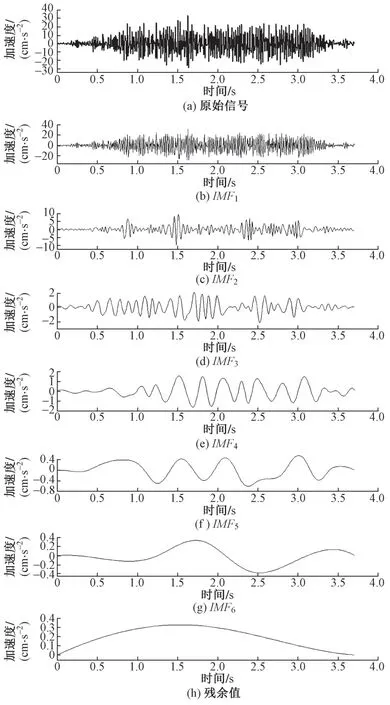
图3 1#测点的加速度响应信号的EMD分解结果

ρxIMFj=1，表示第j阶IMFj与原始数据x完全相关；ρxIMFj=0，表示第j阶IMFj与原始数据x完全无关；|ρxIMFj|在 0～1 取值，表示第j阶IMFj与原始数据x有某种程度的相似。

因此，为了从有限个IMF振动信号中提取有用的信号成分，利用原始数据与每一阶IMFj的相关系数ρxIMFj建立了条件值κ［15］，即

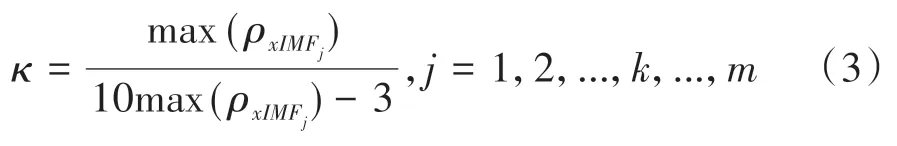
式中，m为IMF的总阶数。

当ρxIMFk≥κ时，表示前k阶IMF与原始数据的相关性强需要保留下来，k+1～m阶的IMF则剔除。根据振动加速度信号EMD 分解各阶IMF的相似度，本文将κ适当减小。对前k阶IMF进行重构，得到与原始数据相关性很强的新信号x˜(t)，即

将各阶IMF信号划分成相关性强和相关性弱的信号（图4），对相关性强的前3阶IMF信号（IMF1～IMF3）进行重构可以得到新的有用信号。

图4 各阶IMF与原始数据的相关性

3.3 频域分析

将相关性强的各阶IMF振动信号进行傅里叶变换，进一步分析桥墩和周围不同场地的振动特性，见图5。可知，列车振动的频率主要集中在10～80 Hz，且随着IMF阶数的增加，高频成分减少。图 5（a）中 3 个测点都在35 Hz 左右频谱出现了峰值，这与轴距为2.5 m 的高速列车以85 m/s 运行速度通过该桥墩的频率对应（f= 85/2.5 = 34 Hz），说明列车运行引起的振动主要受列车轴重的控制；在桥墩右侧的堆积填土上振动在65 Hz时出现了峰值，使得高频成分突出，且频谱峰值的大小为：3#测点＞1#测点＞2#测点。此外，图5（b）和（c）中3个测点的频谱峰值在20，10 Hz左右，这与轨道的不平顺功率谱峰值位置相同，说明列车运行产生的低频振动主要由轨道不平顺控制［16］，且频谱峰值的大小为：3#测点＞2#测点＞1#测点。

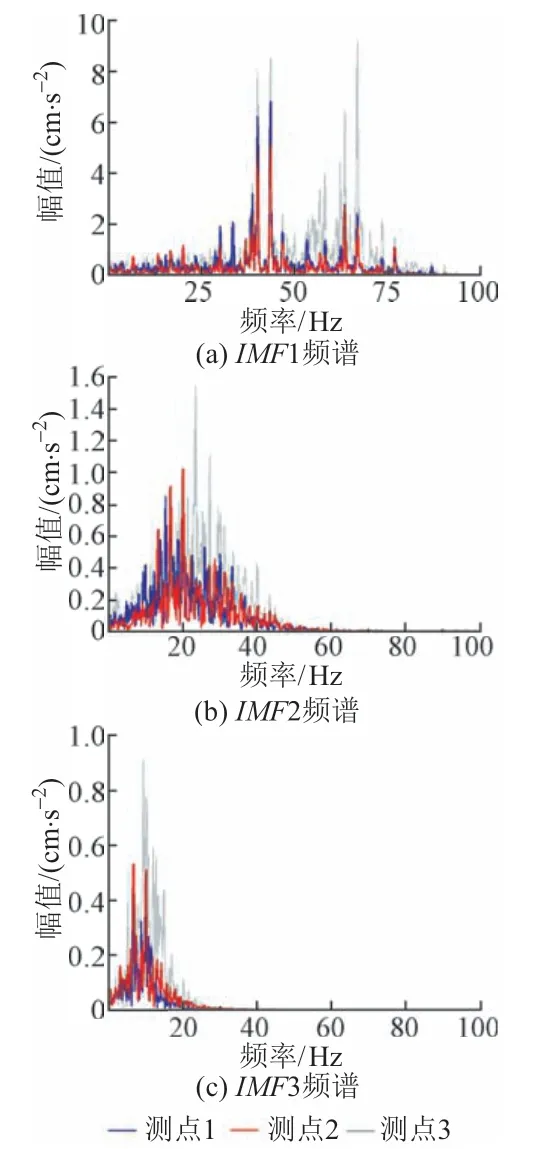
图5 不同测点的各阶IMF振动信号频谱

4 振动数值计算分析

基于现场测试情况，利用有限元数值软件ABAQUS 建立桥墩-桩基-周围场地模型。本文将桥墩顶端支座垫石2#测点的实测加速度时程作为列车振动加速度边界条件，评估列车荷载作用下振动的传播特性。

地面振动主要受场地土体Rayleigh 波速和厚度的影响，波速的大小直接与场地的弹性模量有关［17］。建立桥墩右侧堆积填土在不同弹性模量、高度和长度的模型，采用数值模拟的方法分析堆积填土弹性模量和几何参数变化对振动传播的影响。

4.1 数值模型参数

桥墩和周围场地模型如图6所示。该模型主要包括2 部分：①桥墩，高8.5 m，采用钻孔桩，桥墩和桩均为钢筋混凝土材料，混凝土强度等级为C30。由于钢筋的作用，可将混凝土的力学参数适当提高，即弹性模量为35 GPa，泊松比为0.2，密度为3 500 kg/m3。由于在列车荷载作用下桥墩和桩发生弹性变形，所以假设桥墩和桩为理想弹性材料。②土体，分为4层，服从摩尔-库伦破坏准则，其物理力学参数如表1 所示［18］。本文仅考虑季节性冻土区土体处于冻结和非冻结季时的振动特性，未分析春融时的振动特性。土体物理力学参数包括冻结土体和非冻结土体。

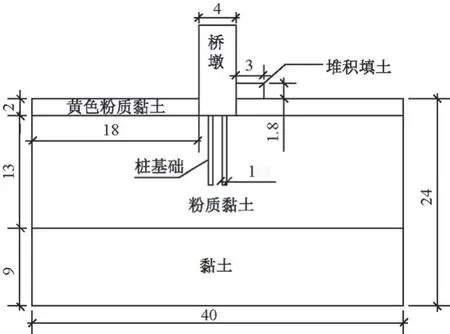
图6 桥墩和周围基础场地模型（单位：m）

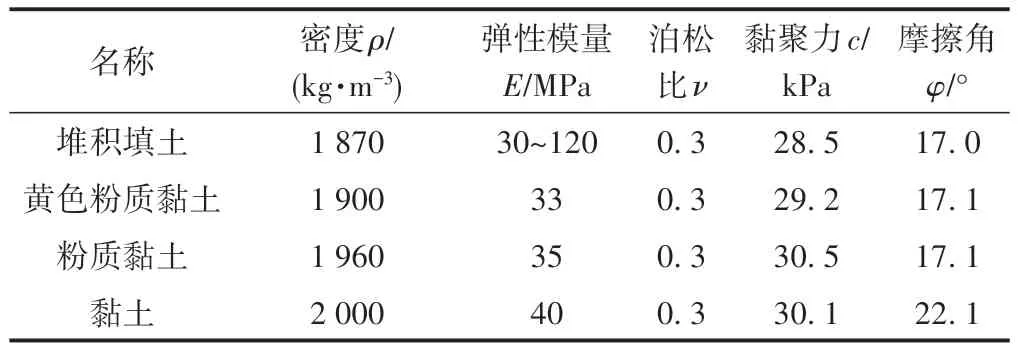
表1 测试区土体的物理力学参数

为了准确计算桥墩和钻孔桩对土体的影响，在桥墩左右两侧土体网格划分比较密集，模型中最大的网格尺寸为1 m×1 m，满足要求［19］。为了防止土体边界对振动波的反射作用，模型土体两侧为CINPE4 无限元单元，模型底端为固定边界，土体和桥墩采用CPE4R 单元。为了分析堆积填土对桥墩左右两侧振动传播特性的影响，分别布置不同的测点（图7）。测点 a—测点 e 距桥墩墩底水平距离R分别为 0，1，3，5，8 m。

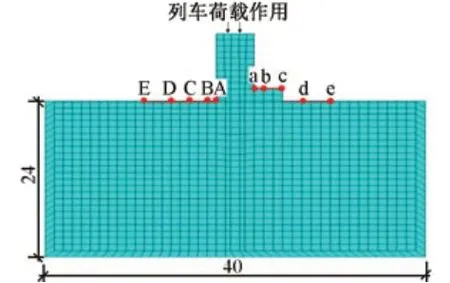
图7 有限元数值模型和测点布置（单位：m）

4.2 数值计算结果分析

为了验证模型的正确性，对3#测点（参见图1）的实测值与计算值进行对比，见图8。可知，实测值与计算值基本一致，能够反映真实情况，说明模型正确可行。

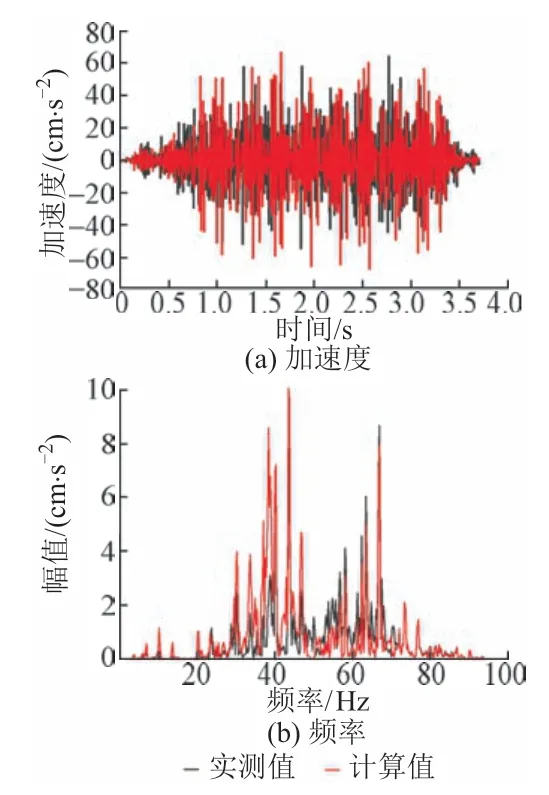
图8 实测值与计算值对比

计算堆积填土的弹性模量E分别为30，60，90，120 MPa 时距桥墩墩底水平距离的加速度峰值，分析右侧场地振动传播以及未堆积填土侧振动传播随距离变化的情况，见图9。

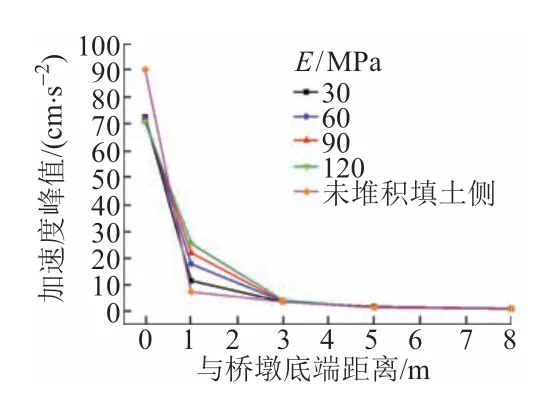
图9 堆积填土弹性模量对振动加速度峰值的影响

由图9 可知：①桥墩两侧的振动加速度峰值随R的增加呈衰减趋势；R=0～1 m时振动加速度峰值迅速衰减，R=1～3 m 时衰减速度减缓，R＞3 m 时衰减速度更缓。②R=0时，堆积填土上的振动加速度峰值小于未堆积填土侧，且随着堆积填土弹性模量的增大略有减小；0＜R＜3 m时，堆积填土上的振动加速度峰值大于未堆积填土侧，且随着弹性模量的增大而增大；R＞3 m时，桥墩左右两侧位于同一场地，不受堆积填土的影响，两侧振动加速度峰值基本相等。这是因为振动波传播到堆积填土的边界上会发生反射作用，使得振动增强，明显大于未堆积填土侧；随着堆积填土弹性模量增大，振动波的传播速度加快，衰减效应减缓。

计算堆积填土的厚度h分别为0，0.8，1.8（实际厚度），2.8和3.8 m时的振动加速度峰值，见图10。

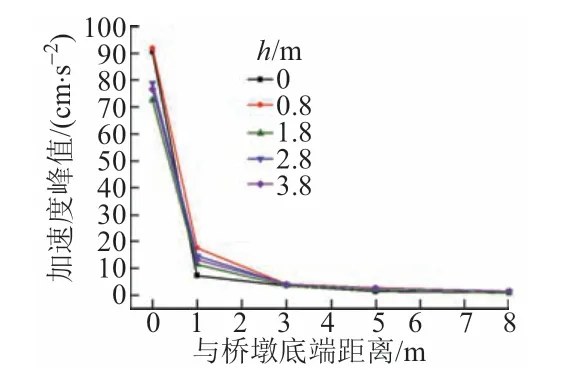
图10 堆积填土厚度对振动加速度峰值的影响

由图10可知：①h=0～1.8 m 时，R=0处的振动加速度峰值随填土厚度的减小而增大，说明填土厚度越小，桥墩与土体的相互作用越强；②h=1.8 m时，R=0处的振动加速度峰值达到最小值；③h＞1.8 m时，R=0处的振动加速度峰值明显增大，但随着厚度的增大又呈减小趋势。这是因为当堆积填土的厚度达到一定程度时，由于土体阻尼作用，振动能量快速消耗，振动减小。R=1～3 m时，堆积填土上的振动加速度峰值明显大于未堆积填土侧，且随着堆积填土厚度的增大呈现减小趋势。R＞3 m 时，堆积填土厚度的变化对振动加速度峰值基本没有影响。

计算堆积填土的长度L分别为2，3（实际长度），4，5 m时的振动加速度峰值，见图11。

图11 堆积填土长度对振动加速度峰值的影响

由图11 可知：①在R=0 处L=3 m 时堆积填土侧的振动加速度峰值达到最小值；②在R=3 m 处L=2 m时堆积填土侧的振动加速度峰值达到最大值；③在除L=3 m 外，长度变化基本不影响振动加速度峰值；R=3 m 时，随着堆积填土长度的增大振动加速度峰值减小，而R=5 m时，随着堆积填土长度的增大振动加速度峰值增大。这是因为当堆积填土的长度增加到一定程度时，振动波在传播过程中明显受到土体阻尼的影响，振动迅速衰减，而在堆积填土的边界附近，由于反射和折射作用使得振动增强。

5 结论

1）在列车荷载作用下，桥墩和周围场地的振动特性明显不同，且不同场地振动特性不同。场地对振动存在放大作用，堆积填土的放大作用更强烈。

2）利用EMD 分解和相关性分析滤掉周围环境激励的影响，并对相关性强的各阶IMF 信号进行傅里叶变化，发现桥墩和场地的振动频率集中在10～80 Hz，且振动在35 Hz 左右出现峰值，这与列车轴重作用的频率一致。由于存在堆积填土，3#测点的振动向高频移动，主频约65 Hz。

3）堆积填土对振动的传播特性有明显的影响，堆积填土侧的振动强于未堆积填土侧。堆积填土的弹性模量和几何参数对地面不同位置的振动程度有明显的影响。