铁路大跨度钢管混凝土拱桥弹性稳定性分析

2020-09-04张继权季日臣

铁道建筑 2020年8期

张继权季日臣

（兰州交通大学土木工程学院，兰州 730070）

钢管混凝土拱桥因其外形美观、跨度大、受力合理、施工简便等优点被广泛运用，我国建成的钢管混凝土拱桥数量多、跨度大［1］。由于拱肋以受压为主，随着钢管混凝土拱桥跨度的增大，宽跨比减小，拱肋横向刚度也变弱［2-4］。对于大跨度拱桥，其稳定问题也日益突出，有必要对影响稳定性的主要因素进行分析。

1 工程概况

银川至西安线银吴铁路银川南特大桥为客运专线，双线铁路桥，线间距为4.6 m。为跨越银川绕城高速采用1 孔128 m 简支系杆拱，简支拱位于直线上，纵向位于平坡及竖曲线上，拱轴线为二次抛物线，理论拱轴线方程为y=0.8x-0.006 25x2，矢跨比f/L=1/5，理论计算跨度L=128 m。拱肋采用外径130 cm、壁厚20 mm 的钢管混凝土空腹哑铃形截面，上下两钢管中心距2.6 m，拱肋截面高3.9 m。拱肋上下钢管之间连接缀板厚20 mm，拱脚缀板间距由130 cm 渐变至70 cm，拱脚缀板间除拱脚面以外2.0 m 范围及吊杆处隔仓灌注混凝土外，其余均不灌注混凝土。全桥设置6 组K 形横撑，每道横撑均为空钢管结构，横撑构造见图1。2 道拱肋共设34 对吊杆，第1 对吊杆距离支点14.4 m，其余吊杆中心间距均为6.2 m。每处吊杆均采用钢绞线整束挤压吊杆，规格为GJ15-17，双吊杆之间纵向间距50 cm，每处吊点系梁设0.35 m厚的隔板。系梁采用预应力混凝土简支箱梁，横截面为单箱双室截面，梁长132.5 m，系梁除梁端局部加高至3.5 m外，其余梁高均为3 m。跨中系梁顶宽15.5 m，底宽13.5 m，拱脚一定范围内梁底加宽至16.1 m，梁顶加宽至16.6 m。系梁跨中边腹板厚55 cm，中腹板厚40 cm，拱脚处分别加厚至185 cm 和130 cm。系梁跨中顶底板厚度分别为40 cm 和35 cm，端部分别加厚至100 cm和80 cm。

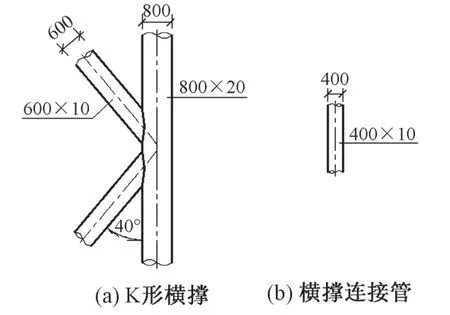
图1 拱肋横撑大样图（单位：mm）

本文通过MIDAS/Civil建立有限元模型，分析了该桥在成桥运营阶段不同荷载工况作用下的稳定性，并通过改变结构设计参数来确定提高稳定性的最佳参数取值。

2 稳定分析的相关理论

结构失稳是指在外力作用下结构的平衡状态开始丧失稳定性，在外力扰动下变形迅速增大，最后使结构遭到破坏［5］。对于钢管混凝土系杆拱桥，拱肋是最容易失稳的部位。结构失稳从空间失稳形态上可分为面外失稳和面内失稳，钢管混凝土系杆拱桥则以面外失稳为主；从失稳性质上可以分为第一类失稳（分支点失稳）和第二类失稳（极值点失稳）［6-7］。第一类失稳采用线弹性屈曲分析，第二类失稳采用非线性弹塑性屈曲分析。本文以线弹性屈曲分析为主。

在分析第一类稳定问题时，假设材料是无限弹性的，并在小挠度的前提下不考虑由于结构构件的安装制作误差、材料的缺陷、荷载能力的偏差等初始缺陷对结构的影响。根据线弹性屈曲理论［5，8］，用有限元平衡方程来表达线弹性失稳现象。在考虑几何初始刚度矩阵下的线形屈曲平衡方程为

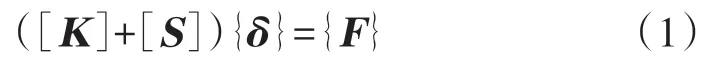
式中：［K］为弹性刚度矩阵；［S］为几何刚度矩阵；｛δ｝为荷载｛F｝作用时的位移。

根据式（1）可知，随着荷载的增加，结构位移增大，当｛F｝增加λ倍时，几何刚度矩阵也增大λ倍，结构的平衡方程［9］为

如果λ足够大，则结构进入随机平衡状态。假设｛δ｝+｛Δδ｝为另一种平衡状态，式（1）依然成立，即

若使式（2）、式（3）均成立，则有

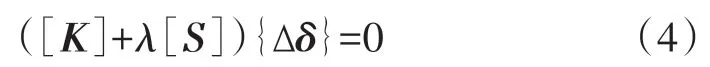
当｛Δδ｝有非零解时，则

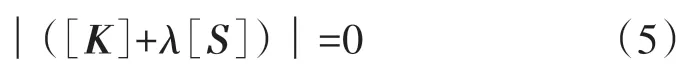
式（5）就是第一类稳定问题的控制方程。求解特征值后，将其从小到大排列，并与结构各阶稳定系数对应。对于工程实际，只有最小稳定系数有意义。

3 有限元模型的建立

采用MIDAS/Civil 建立银吴铁路银川南特大桥128 m 钢管混凝土系杆拱桥模型（图2），该桥为外部静定、内部超静定结构，因此只模拟其上部结构。全桥共有355 个节点，374 个单元，其中系梁、拱肋、横撑、K形横撑均采用梁单元模拟，吊杆用桁架单元模拟；钢管混凝土拱肋为哑铃形截面，采用施工阶段联合截面。

图2 系杆拱桥空间有限元模型

4 弹性稳定性分析

对于大跨度钢管混凝土拱桥，弹性稳定分析方法简单有效，也是目前稳定分析最常用的方法。对全桥成桥运营状态下的稳定性进行特征值分析，考虑2 种荷载工况组合下的稳定性：①工况1，恒载（自重+二期恒载）；②工况2，恒载（自重+二期恒载）+最不利活载。

计算有限元模型在成桥运营状态下前20 阶的稳定安全系数，本文只列出2 种工况下前3 阶稳定安全系数（表1）及对应的失稳模态特征（图3）。

表1 稳定性计算结果

图3 拱桥前3阶失稳模态

由表1及图3可知：

1）前3 阶失稳都是拱肋的面外侧倾失稳，说明增强拱肋的横向刚度尤为重要，以防止发生面外侧倾。

2）2 种工况下第1 阶稳定安全系数在均8.962～10.042，符合拱桥第一类稳定安全系数大于4～5 的要求［10-12］，说明该桥横向稳定性较好。

3）对比2 种工况的稳定安全系数，可以看出整体稳定性以自重和二期恒载为主，活载对全桥稳定性影响相对较小。

5 钢管混凝土拱桥稳定性影响因素

在桥梁设计中通过选择合理的结构参数来提高拱桥的整体稳定性是至关重要的。本文分析成桥运营阶段工况2（恒载+最不利活载）作用下拱肋横撑形式、矢跨比、吊杆非保向力作用对拱桥稳定性的影响，并给出合理的建议。

5.1 横撑形式对结构稳定性的影响

改变横撑形式对拱肋面外稳定影响较大，合理的横撑形式可以明显提高拱桥整体刚度和稳定性［13］。该桥共设6道K形横撑，拱顶两侧对称布置3道。将K形横撑分别换为无横撑、I 形横撑及米字形横撑，对比4 种横撑形式对结构稳定性的影响。4 种体系屈曲计算结果见表2，第1阶屈曲模态见图4。

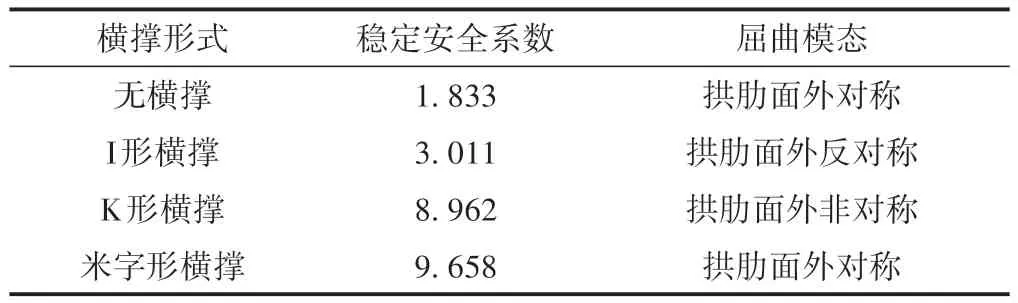
表2 屈曲计算结果

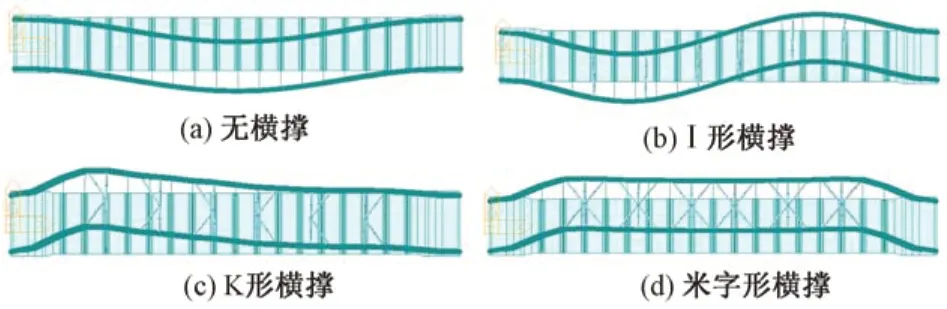
图4 4种体系的第1阶屈曲模态

由表2及图4可知：

1）无横撑及I 形横撑结构稳定安全系数较小，不能满足稳定要求；采用K 形横撑使结构稳定安全系数明显提高，米字形横撑结构的稳定系数最高，二者均能满足稳定要求。

2）相比无横撑结构，采用I 形横撑后结构稳定安全系数提高了64%；在I形横撑基础上增加2道斜撑形成K 形横撑，稳定安全系数比I 形横撑提高了198%，对稳定安全系数的提高最为明显；米字形横撑比K 形横撑稳定安全系数提高了8%。原因是拱肋之间的连接结构对拱圈的抗弯刚度起到关键性作用，横撑可以将2 片独立的拱肋连接成一个空间结构体系，使其具有较大的横向刚度，横向稳定性随之提高。I 形横撑对提高拱圈稳定性的作用不太明显，在采用有斜撑的K 形横撑和米字形横撑后，对拱桥稳定性的提高比较明显。因此，在选择横撑形式时优先考虑这2种横撑。

5.2 矢跨比对结构稳定性的影响

矢跨比对主拱圈的受力有很大影响，是拱桥线形设计的重要参数。在保持拱肋截面、刚度等参数不变的情况下，通过改变矢高来改变矢跨比，分析矢跨比分别为1/7，1/6.5，1/6，1/5.5，1/5，1/4.5，1/4，1/3.5，1/3共9种情况下的稳定安全系数，分析结果见图5。

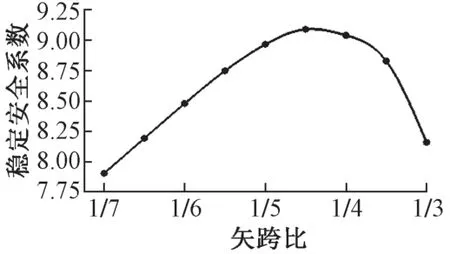
图5 不同矢跨比下稳定安全系数

由图5可知，随着矢跨比的增大，稳定安全系数呈先增大后减小的趋势，与文献［14-15］结论基本一致；矢跨比在1/5～1/4 时稳定安全系数达到了峰值，在1/4.5 时最大。在拱肋抗弯刚度和跨径相同的情况下，若矢跨比很小则拱弧较短，拱肋轴力大，稳定安全系数较小。随着矢跨比的增加，拱弧变长，拱肋轴力变小，稳定性增加；但不是矢跨比越大越好，该桥在矢跨比大于1/4.5 之后稳定安全系数开始减小。综合考虑安全性、拱肋材料用量、建筑高度、施工难易程度和美观性后，矢跨比选择为1/5～1/4较为合理。

5.3 吊杆非保向力对结构稳定性的影响

吊杆是连接拱肋和系梁的主要构件。在其他条件不变的情况下去掉部分吊杆，将吊杆力等效为节点集中力施加在原吊杆与拱肋、系梁连接的位置，对比4种方案下吊杆非保向力对结构稳定性的影响。方案1：去掉所有吊杆，将吊杆力等效为节点集中力。方案2：去掉2，2′，3，3′，4，4′，6，6′，7，7′，8，8′位置吊杆，将吊杆力等效为节点集中力；1，1′，5，5′，9 位置保持不变。方案3：去掉2，2′，4，4′，6，6′，8，8′位置吊杆，将吊杆力等效为节点集中力；1，1′，3，3′，5，5′，7，7′，9 位置保持不变。方案4：所有位置均保留吊杆（与原模型一致）。吊杆位置布置参见图2。

经计算，4 种方案下吊杆非保向力作用下结构的稳定安全系数分别为6.758，7.789，8.240，8.962，且均为拱肋面外非对称失稳模态。由此可知：随着吊杆数量的增加，拱桥的稳定安全系数也逐渐增大；与方案1 的无吊杆形式相比，方案4 结构的稳定安全系数提高了32.6%。这是由于吊杆非保向力的作用，当拱肋有发生侧向位移的趋势时，吊杆发生倾斜，吊杆张力产生了与拱肋位移趋势相反的水平分力，阻止其侧向位移，从而减缓了拱肋的侧倾失稳。随着吊杆数量的增加，吊杆非保向力作用越来越明显。对于下承式双拱肋拱桥，吊杆将拱肋与系梁连成整体，增强了拱桥整体稳定性，相对于裸拱，稳定性更好。