大跨度上承式钢管混凝土拱桥整体稳定性研究

陈佳 胡文军

（1.中铁大桥勘测设计院集团有限公司科研院，武汉 430056；2.中铁大桥勘测设计院集团有限公司第二设计院，武汉 430056）

钢管混凝土拱肋这种特殊的结构形式使钢与混凝土相互作用，提高了拱桥结构抗压承载力，使之跨越能力更大，但随之带来了稳定问题［1］。GB 50923—2013《钢管混凝土拱桥技术规范》规定钢管混凝土拱桥应进行空间稳定性计算，并对弹性稳定特征值作出了规定。大跨度结构的实际稳定安全系数往往远低于弹性稳定特征值，只满足规范中“弹性稳定特征值不小于4.0”的规定，并不能保证结构安全［2］。因此，对大跨度桥梁的第二类稳定安全系数进行分析非常重要。文献［3-7］对上承式钢管混凝土拱桥的稳定性及影响因素做了研究，但大跨度铁路钢管混凝土拱桥尤其是跨度达到500 m 的铁路钢管混凝土拱桥工程实例较少，关于其非线性稳定性的研究也较少。

本文以一座四线铁路大跨度上承式钢管混凝土桁式拱桥为对象，采用线弹性、材料和几何双重非线性有限元分析方法，对多种荷载组合下的结构稳定性能进行计算，分析不同参数对大跨度上承式钢管混凝土拱桥稳定性的影响。该桥主跨500 m，矢跨比为1/4.76，拱轴线为悬链线；主拱由两片四肢全桁式拱肋组成，拱肋平面向内倾形成提篮拱（图1）。拱肋上下弦管直径1.8 m，钢管材料为Q345，壁厚30～60 mm，内灌C60 混凝土。弦管之间通过钢管横联、工字形钢竖杆和斜杆连接形成桁架结构。拱肋截面的宽度和高度都自拱顶向拱脚逐渐增大，以提高结构刚度。

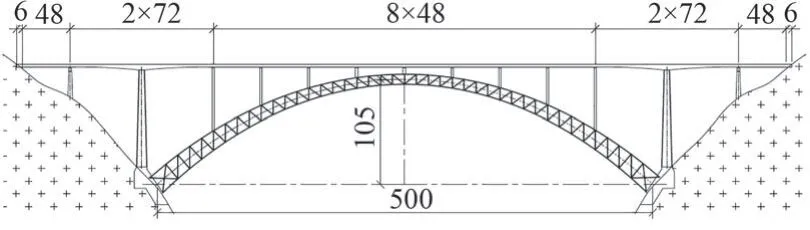
图1 桥梁布置（单位：m）

1 稳定性分析理论

结构失稳问题一般分为2 类：第一类失稳为分支点失稳，即达到某个荷载时，除了原来存在的平衡状态外出现第二个平衡状态，数学处理上是求解特征值问题。求解时假设材料为线弹性，不考虑结构变形二次效应和初始缺陷，因此第一类失稳安全系数通常也称为弹性稳定安全系数。第二类失稳为极值点失稳，考虑初始缺陷、结构变形二次效应（几何非线性）以及材料的弹塑性本构关系（材料非线性）。第二类稳定问题与极限承载力问题具有相同的力学意义。

第一类失稳是理想化情况，实际工程中的大多数失稳都是第二类失稳。由于特征值问题求解方便，在许多情况下弹性稳定问题的屈曲临界值是第二类稳定安全系数的上限，因此研究弹性稳定问题仍有着重要的工程意义。

2 稳定计算模型

2.1 有限元模型

采用ANSYS 建立计算模型。采用双单元法［7］模拟钢筋混凝土拱肋，在拱肋同一个位置建立2个单元，分别赋予钢管、混凝土属性，保证2个单元在节点处变形协调，不考虑二者的相对滑移。拱肋与拱上钢立柱均采用梁单元beam189 模拟。假定主梁、混凝土边墩保持线弹性，不考虑施工过程对结构极限承载力的影响。约束拱肋底部3 个方向的线位移，各边墩底部固结，主梁与拱上立柱之间施加运动耦合约束。

2.2 本构关系

对拱肋钢管约束核心混凝土的本构关系，为考虑高应力水平下混凝土材料非线性，采用文献［8］基于“约束效应系数”得出的混凝土应力-应变关系模型：

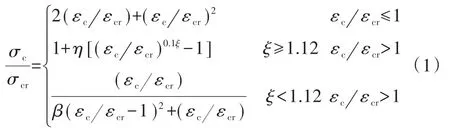
式中：σc，εc分别为核心混凝土的应力、应变；σcr，εcr分别为核心混凝土的峰值应力、应变；ξ为约束效应系数，该系数与钢管混凝土截面的含钢率、钢材屈服强度以及混凝土轴心抗压强度有关；系数η，β与约束效应系数和核心混凝土抗压强度有关，详见文献［3］。

钢材的应力-应变关系采用两折线理想弹塑性模型确定。材料计算参数按规范GB 50923—2013取值。

2.3 荷载组合

计算考虑恒载、列车活载和风荷载。其中恒载包括自重、二期恒载；列车活载根据结构受力特点取轴力最不利工况；静风荷载考虑纵、横2 个方向的风荷载。在不同荷载组合作用下的稳定安全系数见表1。

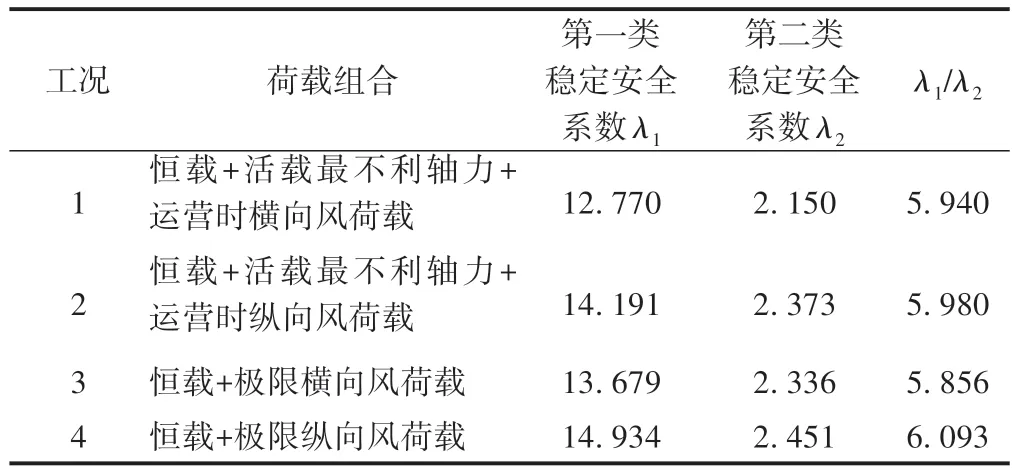
表1 在不同荷载组合作用下的稳定安全系数

在桥梁结构稳定分析时，通常对于荷载稳定安全系数存在2 种不同的计算方法：①将恒载与活载及其他作用荷载同时缩放；②恒载系数不变，只缩放活载和其他作用荷载。为便于分析对比，本文统一按前一种方法计算。

3 计算结果及参数分析

3.1 计算结果

由表1 中的第一类（弹性）稳定计算结果可知，桥梁的弹性稳定安全系数λ1在12.7～14.9，大于规范限值4.0，满足安全要求。通过第2类（双重非线性）稳定分析可知，桥梁的非线性稳定安全系数λ2在2.1～2.5，大于钢材的材料安全系数1.75，且该系数是恒载、活载与风载共同作用下的结果，而实际上恒载的变化是很有限的。对比文献［4］中的结果可知，该桥的结构稳定安全是有保障的。

两类稳定安全系数的计算结果趋势相同，但比值较大，λ1∶λ2在5.8～6.1。包含横向风的荷载组合比包含纵向风的荷载组合更为不利，最小失稳系数都发生在荷载组合工况1。

在荷载组合工况1 作用下，结构的第一阶弹性屈曲模态为拱肋侧向失稳，见图2。结构在承载能力达到极限状态濒临破坏时，背风侧拱脚处下弦管压坏，拱肋面内与侧向耦合失稳，见图3、图4。

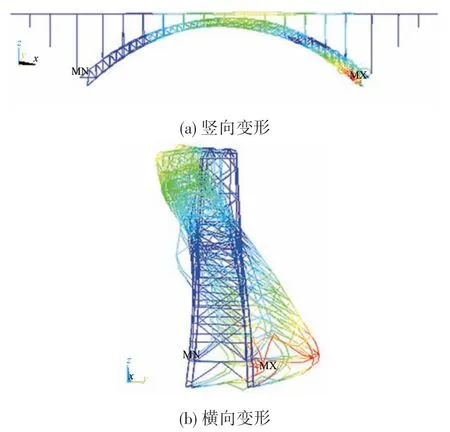
图2 工况1结构侧向失稳模态（第一类稳定分析）

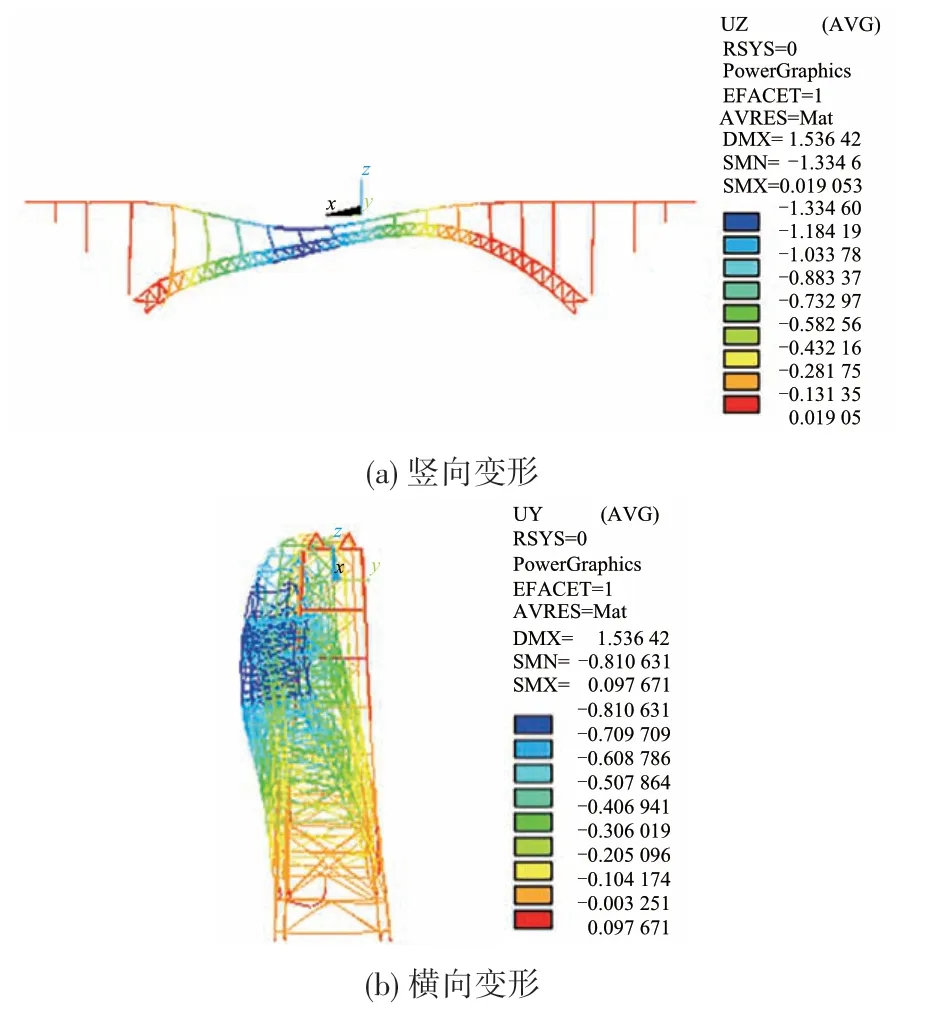
图3 工况1失稳结构变形（第二类稳定分析，单位：m）

图4 工况1失稳结构应力（第二类稳定分析，单位：kPa）

3.2 参数分析

取荷载组合工况1进行双重非线性分析，研究初始缺陷、核心混凝土强度以及拱肋截面含钢率3种因素对结构极限承载能力的影响。为方便比较，以下各表中的影响系数皆以桥梁原模型参数为基准计算得到。

3.2.1 初始缺陷

实际桥梁施工可能产生放样误差，GB 50923—2013规定，钢管拱肋架设轴线偏位允许偏差为L/6 000，其中L为拱肋跨度。桥梁的第一阶弹性屈曲失稳为整体面外侧向失稳，将该形变乘以面外扰动量得到结构初始位移，通过修改模型节点坐标的方式计入初始缺陷。面外缺陷对结构稳定性能的影响见表2。可知，缺陷使结构的稳定安全系数有所降低，但降低幅度很小且低于1%。

表2 面外缺陷对结构稳定性能的影响

3.2.2 核心混凝土强度

钢管内核心混凝土强度的取值直接影响到拱肋的屈服应力，而屈服应力是衡量材料非线性行为的重要指标。核心混凝土标号取C45～C60，对结构稳定安全系数的影响进行分析。核心混凝土强度对结构稳定性的影响见表3。可知，随着混凝土强度的降低，结构的稳定性能也逐渐降低，当混凝土强度等级从C60变化到C45时，稳定安全系数减低了8%。如不考虑核心混凝土的约束效应，稳定安全系数则降低了11.4%，说明钢管对混凝土的约束作用能够大大提高结构的承载能力。

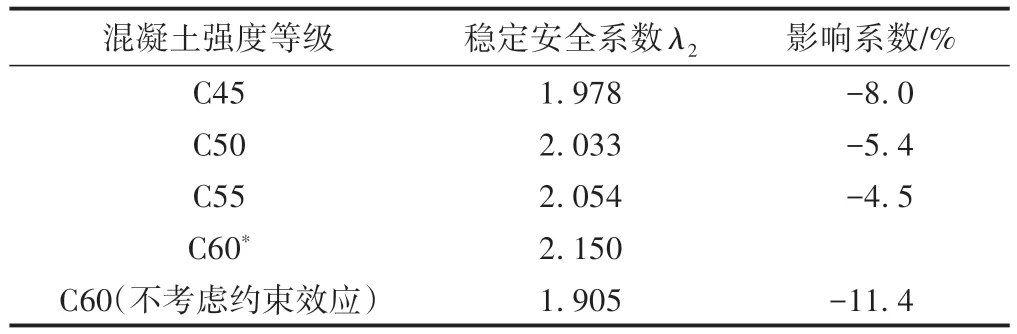
表3 核心混凝土强度对结构稳定性的影响

3.2.3 拱肋截面含钢率

由式（1）可知，拱肋截面含钢率是影响钢管对核心混凝土约束效应的重要参数。根据GB 50923—2013截面含钢率ρc宜为0.04 ～0.20的要求，通过改变含钢率的大小来研究其对结构稳定性能的影响。桥梁拱肋的钢管厚度由拱顶至拱底逐渐增大，截面含钢率在0.070～0.148，以下分别通过增大（或减小）钢管厚度来改变截面含钢率，并根据式（1）相应调整约束效应系数进行分析。

拱肋截面含钢率对结构稳定性能的影响见表4。可知，随着拱肋截面含钢率的提高，结构的稳定安全系数也随之增大。当含钢率在原模型的基础上提高20%，即钢管厚度增加6～13 mm 时，含钢率增加到0.084～0.178，结构的稳定安全系数增加了9.98%。

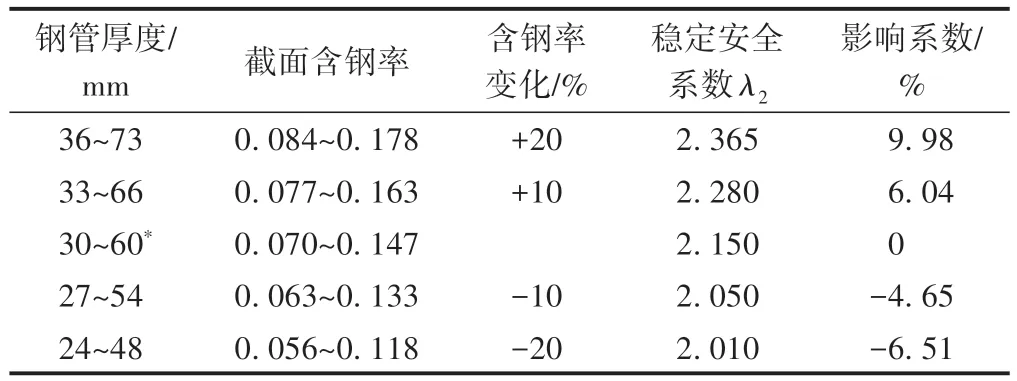
表4 拱肋截面含钢率对结构稳定性能的影响

不同截面含钢率下拱顶处的荷载安全系数-横向位移曲线见图5。可见，高含钢率下结构达到极限荷载时的变形较大，这是由于随着含钢率的提高钢管承受的荷载比例相应增大，且核心混凝土受到的约束效应也逐渐增强，使结构的强度和塑性变形能力得到较大提升。

由以上参数分析可知，混凝土强度和拱肋截面含钢率对结构极限承载能力影响较大，可通过适当提高这2 个参数使结构获得更好的性能。但也有学者指出，钢管内混凝土强度过高可能导致结构发生脆性破坏；含钢率过高亦会降低组合材料的经济性能［6］。

图5 不同截面含钢率下拱顶处的荷载安全系数-横向位移曲线

4 结论

本文以一座大跨度上承式钢管混凝土桁式拱桥为研究对象，在多种荷载组合工况作用下，对结构第一、二类稳定性能进行计算分析，研究探讨了初始缺陷、混凝土强度和截面含钢率对上承式钢管混凝土拱桥稳定性的影响。主要结论如下：

1）结构稳定安全系数满足规范要求。第二类安全系数最小为2.15，仅为第一类稳定安全系数的1/5.8。

2）第一、二类稳定安全系数的计算结果趋势相同，包含横向风的荷载组合比包含纵向风的荷载组合更为不利。

3）混凝土强度和截面含钢率对结构稳定性能影响较大，初始缺陷影响很小。可通过适当提高混凝土强度和截面含钢率使结构获得更好的性能，但应注意混凝土强度过高可能导致的脆性破坏，以及含钢率过高对经济性能的影响。