基于RBF-PID的热风回流焊温度控制
2020-09-03雷翔霄唐春霞徐立娟
雷翔霄,唐春霞,徐立娟
(1.长沙民政职业技术学院 电子信息工程学院,湖南 长沙,410004;2.湖南大学 电气与信息工程学院,湖南 长沙,410082)
电子产品的质量和性能稳定性在很大程度上取决于电路板的焊接质量。电路板的焊接已由小批量手工焊接发展为大批量机器焊接,目前企业常用的焊接设备主要有回流焊、波峰焊等。回流焊是表面组装工艺的核心工艺,亦是目前应用较广泛的批量生产焊接技术,批量的电路板通过传送带缓慢送至回流焊机的炉膛当中,在几分钟内成百上千个焊点自动完成焊接。回流焊机的焊接温度直接影响电子元器件的焊接质量和电路板的性能,据统计,因回流焊机焊接温度不当而引起的焊接缺陷主要有虚焊和元器件损坏等[1]。由此可见,提高回流焊机的温度控制精度对提高焊接质量起着举足轻重的作用,回流焊机的焊接温度精度与系统本身参数和控制算法有相当紧密的关系,研究回流焊机的数学模型和选用合适的温度控制算法有重要的工程实践意义。
常规PID控制具有结构简单,响应速度快等优势,广泛应用于温度控制、水位控制、速度控制等工业控制中。但常规PID控制器的参数确定依赖于技术人员的经验,未能对PID参数进行在线自整定,故在非线性、时变性和滞后性系统中的控制精度不高。温度控制系统作为典型的时变性和滞后性系统,当采用PID控制时,需要针对被控对象进行参数整定。众多研究者对PID参数在线整定进行了大量的研究,提出了各种整定算法,如临界灵敏度法、基于增益优化的整定法、ISTE最优设定方法以及各种优化算法。汪洋和王琪[2]分析了中频炉温度控制系统的数学模型,选用模糊免疫PID控制,对中频炉的PID控制参数进行在线调节,取得了满意的控温精度。郑辉[3]利用能量补偿预测和热量迭代算法改进常规PID控制算法,并将其在MATLAB中进行仿真实验,取得了一定的成效。马玉国[4]将二维模糊PID算法应用于回流焊机温度控制系统中,在实物验证中,控温精度为±2℃。戴建华[5]采用西门子S7-200PLC与EM231模拟量模块作为控制器,设计模糊自整定PID控制,在HW-RF8800C型再流焊机上进行实际控制,控温效果令人满意。曾驰鹤[6]选用西门子S7-200PLC作为主控器,设计BP神经网络PID算法应用于回流焊温度控制系统中,在MATLAB仿真中取得了良好的效果。
热风回流焊温度控制作为温度控制的一种,同样具有非线性和滞后性特点。鲁五一等[7-8]等通过积分分离PID控制算法对该系统进行仿真和实验验证,取得了较好的成效。回流焊精确数学模型可以从热力学的角度建立,但该模型的建立需要了解工艺过程,建立过程复杂并且实用性不强[9]。
径向基神经网络(radial basis function,RBF)为具有单隐含层的3层前向网络,具有较强的自学习和自适应能力,在逼近能力、分类能力以及学习速度等方面都优于BP神经网络;能够以任意精度逼近任意连续函数以及克服局部最小值的能力。本文在分析回流焊机工作过程中的热平衡,建立回流焊机的简要数学模型的基础上,设计基于RBF-PID控制算法对回流焊机的温度进行控制。该算法充分发挥了PID控制结构简单、响应速度快的优点和RBF神经网络的自学习、以任意精度逼近任意连续函数以及克服局部最小值的能力,根据外界变化适时在线调整PID控制算法的3个参数,在实际控温过程中提高了系统的控温精度和稳定性。
1 回流焊机温度系统数学模型建立
回流焊机的内部结构如图1所示。炉胆内部从左到右分为8个温区,其中1和2温区为预热区,进入回流焊机的待焊接电路板在此区域进行预热;3,4和5温区为保温区,预热后的电路板在此区域充分受热均匀;6和7温区为回流区,即焊接区;最后的第8温区为冷却区。带柱链条带动待焊接的PCB电路板匀速通过炉胆部位。
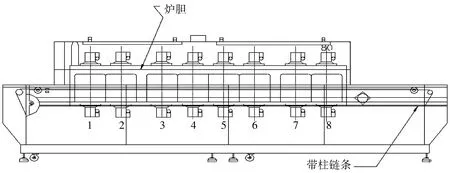
图1 回流焊机结构示意图
为简化回流焊温控系统的数学模型,做如下假设:
1)炉胆与炉膛之间用隔热石棉隔开,不考虑彼此之间的热量交换;
2)同一温区的空气成分一致,即同一温区中空气的物理参数一致,空气在同一温区的上下对流过程中,只存在质量的交换,不存在热量交换;
3)同一温区为一整体,内部各点的温度一致,不考虑温区边缘微小的温度变化。
根据热力学第一定律,将某一温区看作1个整体,则流入、流出该温区的能量守恒。现以第4温区为例推导系统的热平衡方程,有:
Q4入=Q4出
(1)
Q4入=ChHh(t)(t-Td)
(2)
(3)
Vb(t)=vst
(4)
式中:Q4入和Q4出分别为第4温区的输入、输出热量;Q3-4,Q4-5和Q炉壁分别为第4温区向第3温区、第5温区和炉壁的辐射热;QPCB和Q链条分别为PCB板带走的热量和链条带走的热量;T5,T4和T3分别为随时间变化的第5温区、第4温区和第3温区的瞬时温度;Ch为回流焊加热源的传导系数;Hh(t)为回流焊加热设施输出的函数;ρ为空气密度,1.2 kg/m3;Cρ为炉胆内气体定容比热容,1.005 J/(kg·℃)[10];hc为回流焊机保温层与炉胆温区内气体的热交换系数;Ac为回流焊机保温层的面积,m2;Vin为PCB板流动时所带动的回流焊机炉胆内的空气流动率,m3/s;ρb为PCB基板的密度,1.9 g/cm3;Cb为PCB基板在20℃的定容比热容,1.28 kJ/(kg·℃)FR-4铜材质[11];Vb为单位时间内通过回流焊机第3温区的PCB板的体积,m3;v为回流焊机传送带的速度,m/s;S为PCB板的截面面积,m2;t为时间,s;。
综合式(1),(2),(3)和(4)并做适当变换得到回流焊第四温区的温度动态模型关系为
(5)
现场测试得知,回流焊机工作期间,其外表面的温度基本维持在30~40 ℃不变,即回流焊机的保温层工作良好,炉胆内的温度对外辐射的能量恒定且较少,因此,在实际温度控制时将它作为一个恒定量,不予以考虑,则式(5)可变化为
(6)
整理式(6)得
(7)
H(t)=ρCρVin(t)+ρbCbVb(t)
(8)
将式(8)代入式(7),则有
(9)
H(t)取决于回流焊保温区的炉胆内气体定容比、第4温区炉胆体积、PCB的材质、PCB板的面积和传送链条的速度等。
在一个生产班组中,PCB的材质和大小基本一致,由于前述工序所耗时间大体相当,故传送链条的速度基本相同,因此,可将H(t)看做一个常数,用一个近似参考值κ代替,有
(10)
式(10)两端进行Laplace变化并整理得:
(11)
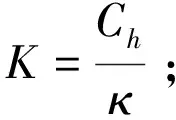
2 RBF-PID控制算法
2.1 RBF神经网络
RBF神经网络是由输入层、输出层和隐含层构成的3层前向网络,具有最强逼近能力和克服局部极小值的能力。输入层与隐含层之间的映射关系为非线性映射,输入层分别对应目标温度rin,实测温度yout和温度偏差ek,隐含层与输出层之间的映射关系为线性映射,输出层分别对应PID中的比例系数kp,积分系数ki和微分系数kd,通过参数动态调节找到近似最优的PID参数,获取最佳逼近性能,网络结构见图2。

图2 径向基神经网络结构图
网络输出为
(12)
其中:W=[wi1,wi2,…,wi5]T为神经网络权矢量;H=[h1,h2,…,h5]T为径向基矢量;φ为线性激活函数;hi为高斯核函数,见式(13)[12]所示。
(13)
其中:x为输入向量;Ci为径向基函数的中心,与输入向量x的维数一致。
取神经网络的目标函数为[13]
(14)
RBF神经网络的输出权值,节点中心和节点基宽参数采用文献[12]所用迭代算法,见式(15)~(17)。
wj(k)=wj(k-1)+η[y(k)-ym(k)]+α[wj(k-1)-wj(k-2)]
(15)
(16)
(17)
其中:η为学习效率;α为动量因子,且η,α∈[0,1]。
2.2 RBF-PID控制系统设计
RBF神经网络有极强的自学习、自适应能力,能收敛到全局最优解,故可用于在线调整PID控制器的参数,从而弥补PID控制器参数未能随外界参数变化而变化的不足,构成一个具有自适应、自调节能力的控制器。诸多研究者将径向基函数神经网络与PID控制算法结合并应用于控制系统中,取得了良好的效果[12,14-15]。基于此,文中将RBF与PID结合应用于回流焊温度控制系统中,系统控制原理图如图3所示。
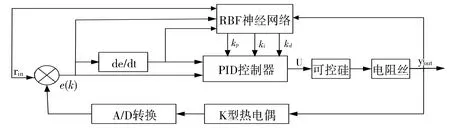
图3 系统控制原理图
热风回流焊机k时刻的输入为r(k),输出为y(k),则系统的误差为
e(k)=r(k)-y(k)
(18)
则增量式PID控制算法可表示为
Δu(k)=kp[e(k)-e(k-1)]+kie(k)+kd[e(k)-2e(k-1)+e(k-2)]
(19)
(20)
其中:
(21)
由式(19),(20)和(21)可得热风回流焊机温度控制的输出增量为
(22)
3 回流焊温度控制系统实验结果分析
将前述构建的RBF-PID控制算法应用于回流焊机保温区3,4和5温区的温度控制中,第3区的目标温度为100 ℃,第4温区的目标温度为110 ℃,第5温区的目标温度为120 ℃。选取RBF网络基函数σ=0.65,加权系数w1=0.01,w2=0.02,w3=0.01,学习效率η=0.3,动量因子α=0.05。
3.1 稳态性能实验
回流焊机的稳态实验为回流焊机中无PCB板焊接时的实验,此时,回流焊机链条保持不动,由于回流焊机的保温效果相对较好,对外几乎不产生热辐射,回流焊机的温度控制实验结果如图4所示,第3和4温区的目标温度为270 ℃,第5温区的目标温度为280 ℃。

图4 系统稳态实验曲线图
3.2 动态试验
回流焊机链条的速度为0.05 m/s,PCB板的长×宽为200 mm×100 mm,PCB的上料速度恒定。实验结果如图5所示。
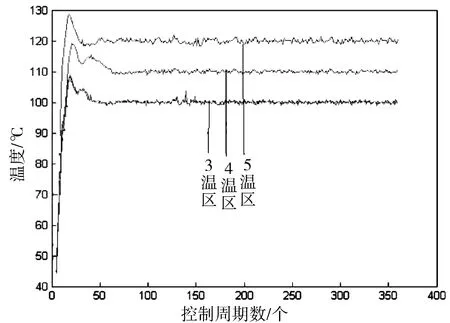
图5 回流焊3,4和5温区的实验曲线图
从图5可看出,在采用RBF-PID控制算法的回流焊温度控制系统中,系统的超调量为9%,稳态误差为±1.5 ℃,比文献[4]中的稳态误差要小。当回流焊的第三温区在140个控温周期时受到干扰,能在5个控温周期内重新达到稳定。RBF-PID控制能使回流焊温度输出较好的跟踪给定温度值,在PCB焊接过程中,系统的温度稳定性较好,系统的收敛速度和控制精度等方面都得到较大提高。
4 结论
本文利用热平衡原理,以回流焊某一温区为对象推导了回流焊机的温度控制数学模型,采用RBF-PID控制算法对回流焊机温度控制系统进行实验验证,结果表明RBF-PID控制能充分发挥神经网络具有较强逼近任意非线性函数的映射能力和自学习能力,提高了回流焊机温度控制的动态响应速度和控温精度,具有较强的工程实践意义。
