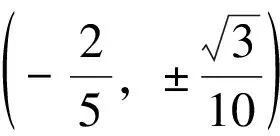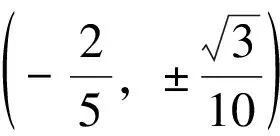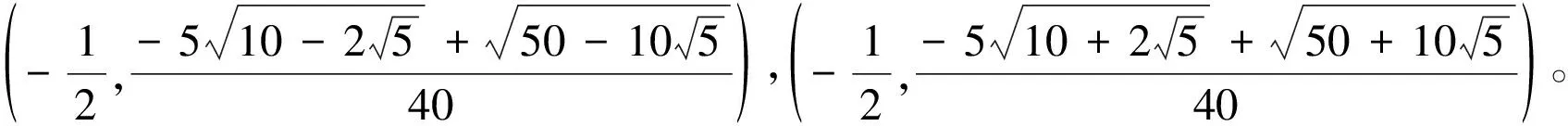一类平面九次微分系统的广义中心条件与极限环分支

刘灿辉,杜超雄

(长沙师范学院 数学科学学院,湖南 长沙,410100)

本文主要研究如下一类平面九次微分系统的广义中心条件与极限环分支问题:

(1)

其中：

P0=y(3x4+12x5+20x6+16x7+6x2y2+56x3y2+104x4y2+72x5y2+3y4+12xy4+84x2y4+96x3y4+40xy6),

P1=3x5+14x6+24x7+18x8+6x3y2+42x4y2+84x5y2+68x6y2+3xy4-6x2y4+32x3y4+72x4y4-2y6-28xy6+12x2y6-10y8,

P2=5y(1+2x)3(x2+y2)2,

P3=-5(1+2x)2(x+x2-y2)(x2+y2)2,δ,A10,B10∈R。

平面多项式微分系统的极限环分支问题往往与Hilbert第16问题紧密相关。对于n次系统分支出的极限环数目也称之为Hilbert数。多项式微分系统的Hilbert数的研究是一个热点问题,SHI[1]得出二次多项式系统可分支出4个极限环；YU等[2-3]得出三次系统的Hilbert数不少于12,LIU和LI[4]得出三次系统的Hilbert数不少于13,这是目前关于H(3)的最好结果。对于其他类型的微分系统的极限环分支问题,研究结论众多,如文献[5-10]。可能由于计算的复杂性,对于高次系统Hilbert数的研究结论相对较少。

本文将着力于讨论上面的九次系统的极限环分支问题,并给出其同步Hopf分支的实例,得出该系统可以分支出15个极限环,其中包含由4个初等奇点分支出的12个小振幅极限环和由无穷远点分支出的3个大振幅极限环。此外,还给出了其广义中心条件。本文的结论是对现有结论的有益补充。

1 焦点量的计算方法

本文主要采用文献[5]中关于焦点量的计算方法,具体如下。

考虑以下Poincaré型实系统：

(2)

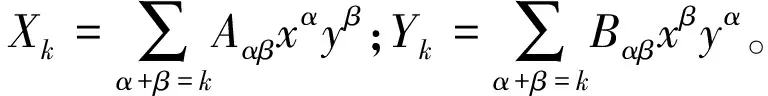
系统(2)|δ=0经变换

(3)

化为如下复系统:

(4)

这里z,w和T为复变量且

显然，系统(4)的系数满足共轭关系，即:aαβ与bαβ互为共轭复数。其中,

α≥0,β≥0,α+β≥2,aαβ=Aαβ+iBαβ,bαβ=Aαβ-iBαβ。

这里称系统(2)|δ=0与(4)互为伴随系统,定义见文献[5]。

引理1[5]对系统(4),可逐项确定形式级数:

使得

其中：μm是系统(4)原点的第m个奇点量,与系统(2)|δ=0用Poincaré形式级数法求得的第m个焦点量v2m+1有关系，v2m+1～iπμm,m=1,2,3…。

在引理1中,记号“～”表示代数等价,定义见文献[5]。

对充分小的h和ε,若h=h(ε)是Δ(h,ε)的1个零点,则h=-r(π,h(ε),ε)也是Δ(h,ε)的1个零点,从而在实域内Δ(h,ε)的正负零点成对出现。

基本条件1[5]存在自然数N,m和一串与ε无关的λ0,λ1…,λk…，使

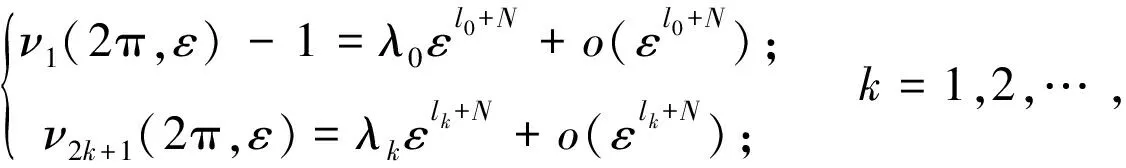
lm=0,λm≠0。

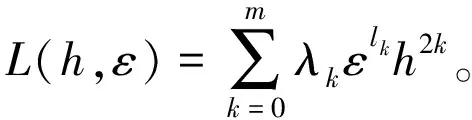
引理3[5]对于系统(2)而言,

1)若基本条件1成立,则系统(2)当0<|ε|≪1时，在原点充分小的邻域内至多可由焦点或中心点扰动出m个极限环。

2)若基本条件1成立且基本条件1中λkλk-1<0,(k=1,2,…m),以及lk-1-lk>lk-lk+1,k=1,2,…,m-1,则当0<|ε|≪1时，其弱分支函数L(h,ε)恰有m个正零点,即

相应地,系统(2)的原点可分支出m个极限环,其位置分别在圆x2+y2=(-λk-1/λk)εlk-1-lk的附近。

2 系统(1)的广义焦点量与广义中心

为了研究系统(1)的极限环分支问题和广义中心问题,焦点量的计算显得很关键。但是对于系统(1),其形式并不满足系统(2)的标准形式,故无法直接利用系统(2)的焦点量的计算方法来进行计算,因此，这里有必要先作几个合适的变换。

通过Bendixson倒径变换

(5)

与时间变换

dt=5(x2+y2)4dτ

(6)

系统(1)变成了如下的实系统:

(7)

在变换公式(5)和(6)下,系统(1)的无穷远点和4个初等奇点

对于系统(7),有下列结论。

定理1系统(7)是一个关于点(-1,0)Z5等变对称的多项式系统。

证明系统(7)|δ=0在变换u=x-1,v=y下变成了如下系统：

(8)

系统(8)在旋转变换

下保持不变,因此，系统(8)是关于原点Z5等变对称的多项式系统,它有5个关于原点等变对称的具有相同拓扑结构的奇点:

又因为系统(8)是系统(7)在变换u=x-1,v=y下得到的,因此,系统(7)是一个关于点(-1,0)Z5等变对称的多项式系统。证毕。

Q 1:燃烧室输出到水浴的热量;Q 2:水浴传递给管程内LNG的热量;C:水的热容;T 1:水浴温度;T 2:管程LNG的温度;R:水浴传热热阻;Gp 1:主被控对象(NG出口温度);Gp 2:副被控对象(水浴温度);Gc1:主回路控制器;Gc2:副回路控制器;τ:副被控对象时滞;τ1:主控对象存在时滞;J(s):燃料气的干扰;E(s):入口LNG的干扰;GE(s):入口LNG的传递函数;Ge(s):前馈补偿通道函数;Y 1(s):主回路的输出;Y 2(s):副回路的输出。

由于平移变换不改变系统的拓扑结构,因此，研究系统(7)的原点和4个初等奇点的极限环分支与中心问题，只需要先考虑系统(8)的5个相应奇点的对应性质，且在Bendixson倒径变换下,系统(1)的分支行为和广义中心条件与系统(7)是保持一致的。一般来说,中心问题是相对于初等奇点来讨论的,对于具有可积性的无穷远点或者在初等变换下可化为可积的初等奇点,可以称之为广义中心。那么,如果系统(8)的5个奇点是5个中心时,系统(1)的无穷远点和4个初等奇点为5个广义中心。相似地,由于系统(8)是系统(1)通过初等变换而得到,故系统(8)的奇点的焦点量可以称为系统(1)的对应奇点的广义焦点量。

为了研究系统(1)的极限环分支行为和中心焦点问题,不妨先计算其广义焦点量。通过变换:

系统(8)变为

(9)

根据引理1的计算方法,可以得到系统(9)|δ=0的原点的前三阶奇点量。

定理2系统(1)的无穷远点和4个初等奇点的前三阶广义奇点量为系统(9)|δ=0原点的前三阶奇点量,其表达式如下:

由引理2～3和定理2,可以得到如下定理。

定理3系统(1)的无穷远点和4个初等奇点的前三阶广义焦点量为系统(8)|δ=0原点的前三阶焦点量,其表达式如下:

分析定理3中焦点量的结构,可以知道以下结论。

定理4系统(1)的无穷远点和4个初等奇点的前三阶广义焦点量为0(或者系统(8)|δ=0的原点的前三阶焦点量为0)的必要条件是B10=0。

焦点量为0是奇点成为中心的必要条件,有必要找出其充分条件。进一步可证明定理4中的条件也将成为系统(1)的无穷远点和4个初等奇点成为广义中心的充要条件。

定理5系统(7)|δ=0的5个初等奇点为同步中心的充要条件是B10=0。

证明根据定理4知道,必要条件显然成立。

下面证明充分性。当B10=0时,系统(7)|δ=0变成了

(10)

系统(10)有如下形式的通积分:

3(10u2+45u3+60u4+29u5+5u6+40v2+145uv2+70u3v2+15u4v2+25uv4+15u2v4+5v6)+3iv(v4-10u2v2+15v2+5u4-45u2-30u)+25A10(3u2+7u3+12u4+6u5+u6-3v2+3uv2+12u2v2+12u3v2+3u4v2+v6)-25iA10v(-6u+3u2-v2)=C(C为常数)。

因此,当B10=0时,系统(7)|δ=0的5个初等奇点为同步中心。证毕。

进一步,由于系统(7)是系统(1)通过变换公式(5)和(6)得到的,因此，有如下结论。

定理6系统(1)|δ=0的4个初等奇点和无穷远点为5个同步中心的充要条件是B10=0。

3 系统(1)的极限环分支

上面的计算已经得出系统(1)的前三阶焦点量表达式,下面考虑其极限环分支问题。

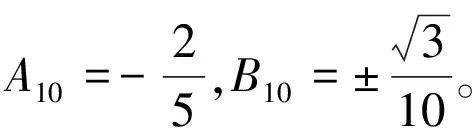
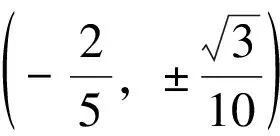
(11)

证明在上面形式的扰动下,系统(7)的5个细焦点的焦点量分别为

v1(2π,ε,δ)=c0ε6+o(ε6),

v3(2π,ε,δ)=c1ε4+o(ε4),

v5(2π,ε,δ)=c2ε2+o(ε2),

v7(2π,ε,δ)=c3+o(1),

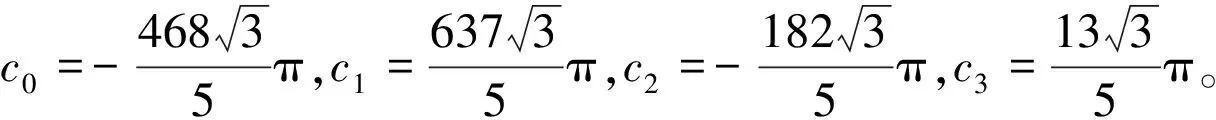
d(εh)=r(2π,εh)-εh=

(v1(2π,ε,δ)-1)εh+v2(2π,ε,δ)(εh)2+v3(2π,ε,δ)(εh)3+…=

πε7h[g(h)+εhG(h,ε)]

(12)

其中：g(h)=c0+c1h2+c2h4+c3h6=c3(h2-1)(h2-4)(h2-9)。

根据(12)和隐函数存在定理,d(εh)有3个简单正零点,它们靠近g(h)的零点1,2,3。因此，系统(8)的原点可以分支出3个极限环,这3个极限环分布在圆u2+v2=m2ε2(m=1,2,3)的周围。证毕。

由系统(1)与系统(7)及系统(8)的关系,可以得到下面定理。