三角形五元十字混合阵列弹丸落点定位方法
2020-09-02张鸿涛纪春佳
王 洋,张鸿涛,纪春佳
(1.中北大学,山西 太原 030051;2.北方华安工业集团有限公司,黑龙江 齐齐哈尔 161046)
0 引言
弹丸回收是武器试验和射击检测中一项重要的工作。目前靶场对于弹丸回收的常用方法有光学法和人工搜索法两种[1]。光学法是利用光学仪器以及基站坐标对弹丸落点进行定位,但易受到温度、湿度及地形等环境影响,产生较大的误差[2]。人工搜索法是通过耗费大量人力来寻找弹丸,不仅强度大、效率低,还有非常高的风险,甚至有时会找不到弹丸。目前快速准确定位落点的研究主要是有源主动式探测和无源被动式探测两种[3]。有源主动式探测是通过辐射电磁波为主要途径,通过基站信号发射器发射特定的探测信号,再经过接收基站接收反馈信号,完成对目标的定位;无源被动式探测是通过被动接收外部的信号完成对目标的定位。因为无源被动式探测技术不会主动发射信号,隐蔽性高,因此可以完成一些隐秘性较高或抗干扰能力弱的任务[4-5]。
通过声传感器定位是被动式探测常用方式,原理是依靠声传感器阵列收集弹丸落地的声响,通过计算确定弹丸落点[6-7],不仅加快了对弹丸落点的定位,极大地减少了人力物力的消耗,降低了危险性,还提高了定位精度。分析了基于五元十字阵的单基阵和双基阵对弹丸落点的定位精度,定位误差较大[8]。针对靶场弹丸回收试验中弹丸落点定位精度低的问题,提出基于三个五元十字阵列组成三角形混合阵列的定位方法。
1 五元十字阵列定位
1.1 五元十字单基阵定位
1.1.1五元十字单基阵模型
图1为单基阵的排列图(本文不考虑俯仰角)。四个传感器与中心传感器的间距都为D,建立直角坐标系,中心传感器位于原点,即O(0,0)。边缘传感器坐标分别为P1(D,0),P2(0,D),P3(-D,0),P4(0,-D)。设T为弹丸落点,则T与中心传感器O的距离为r,与边缘传感器的距离为r1,r2,r3,r4。传感器接收从声源T传来的声音信号,中心传感器与边缘传感器接收到信号的时间差为τi(i=1,2,3,4),设声速为c时,声波距中心传感器与边缘传感器的距离差为di(i=1,2,3,4),则有di=c×τi。
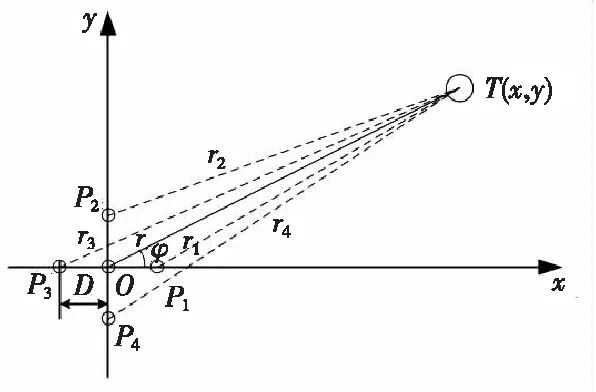
图1 单基阵模型Fig.1 Single array model
根据阵列的几何关系得:
(1)
将式(1)展开相互抵消可以得到:
(2)
由于弹丸落点较远,声波距中心传感器与边缘传感器的距离差di远小于弹丸落点,可得:
(3)
(4)
1.1.2误差分析
基阵选择同一型号的传感器,因此设定每一个传感器的时延误差都相同,即每个传感器的时延标准差都相同,στ=στ1=στ2=στ3=στ4。五元十字定位法主要是通过接收声源到传感器时的距离和方位角进行对声源的定位。
根据误差传播理论可得,五元十字单基阵定位的距离标准差[9]为:
(5)
由式(5)可以看出,基阵对声源距离误差标准差与距中心传感器的距离、声速、传感器间的距离以及时延误差标准差有关。
设定c=343.6 m/s,στ=50 μs,图2所示为距离误差随着传感器间距D以及声源与中心传感器距离的变化图。
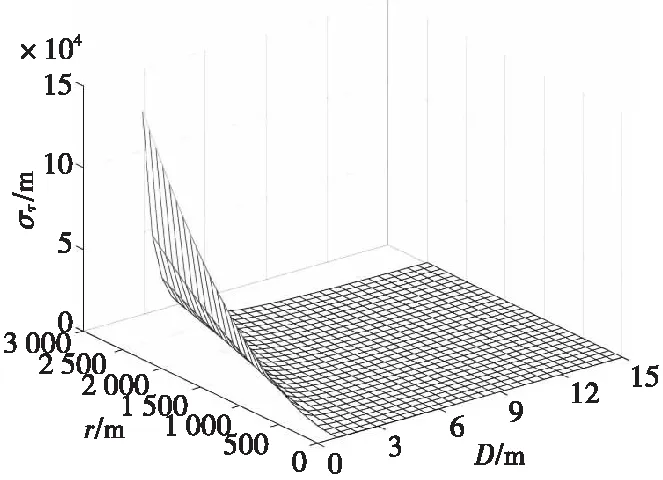
图2 距离误差随间距和距离变化关系Fig.2 The relationship between distance error and distance
随着传感器间距的增大,误差逐渐变小,当传感器间距为9 m时,声源距离r=2 000 m时,距离误差σr=1 000 m。而随着声源距离的增大,对于距离的测量出现了较大的偏差。取特定的间距D=3 m,6 m,9 m,12 m,距离误差随间距变化关系如图3所示。

图3 距离误差随间距变化关系Fig.3 The relationship between distance error and distance
由图3可以得出结论,五元十字单基阵定位对于距离的定位误差较大,无法满足1%的精度要求。
与测距误差相似,方位角误差标准差:
(6)
由式(6)得,方位角误差标准差与声速、传感器间距以及时延误差标准差有关。图4设定στ=50 μs,方位角误差标准差随声速以及传感器间距变化的变化图。
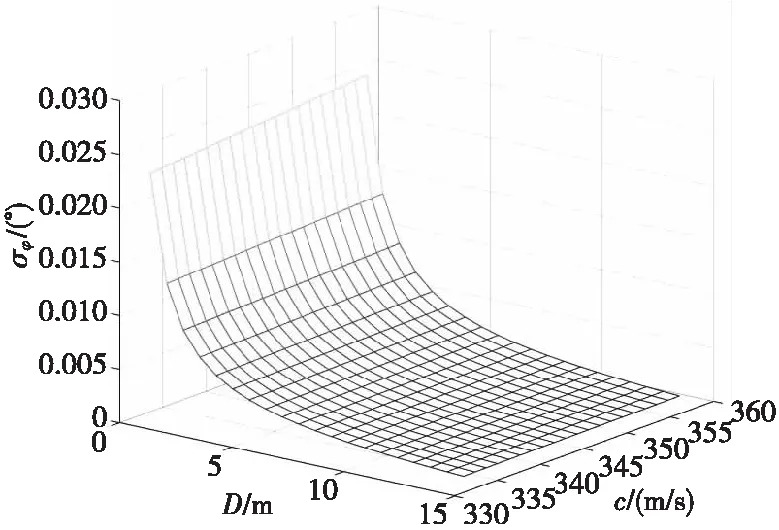
图4 方位角误差与间距和声速变化关系Fig.4 The relationship between azimuth error and the variation of spacing and sound velocity
由图4得,方位角的偏差与声速呈正比,随着声速的增加方位角误差标准差增大。传感器间距对方位角定位影响较大,在传感器间距D>6 m时逐渐趋于平缓,而在D≥9 m时方位角误差标准差稳定在0.002 3°上下浮动。因此增大传感器间距可以有效地提高方位角的定位精度。
由上述分析可知,五元十字单基阵对于声源定位时,当声源距离r≥1 300 m,误差σ>500 m,无法达到1%的定位精度要求,单基阵不能准确地对弹丸落点定位。
1.2 五元十字双基阵定位
1.2.1五元十字双基阵模型
由于单基阵不能准确地定位落点的位置,因此采用双基阵对落点进行定位[7-8],由于五元十字定位法可以较为准确地定位出方位角,因此可以通过两个五元十字阵列组成双基阵,分别确定每个基阵的方位角,通过延长线交叉的方法提高定位精度。

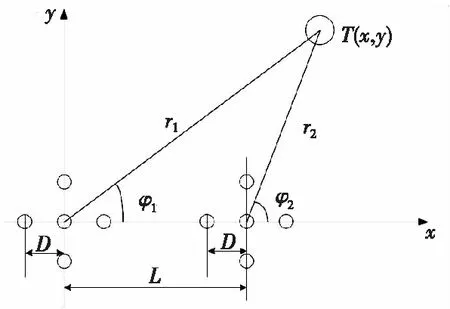
图5 五元十字双基阵模型Fig.5 Double array model
观察图1与图5可知,图1与图5具有相同的几何关系,则由式(3)可得:
(7)
由式(7)得出五元十字双基阵的落点(x,y)的计算方程:
(8)
由式(8)可知,可以由两个基阵的方位角通过计算得到声源的位置。
1.2.2误差分析

通过图5几何关系可得:
(9)
因此通过误差传播理论[9]可知,测距的标准差为:
(10)
式(10)中,设定声速c=343.6 m/s,传感器间距D=9 m,στ=50 μs,两基阵中心传感器间距L=30 m,可以得到图6。由图6可知:在传感器间距与延时误差为定值,第二基阵方位角在φ2=(5°,175°),且当落点在距离基阵1 500 m时,可将误差控制在1.5%;但是当方位角在φ2=(-5°,5°)∪(175°,185°)时,尤其在φ2=0°及φ2=180°时,误差会快速增大。由表1可知,当弹丸落点在一定范围内,双基阵可以基本准确的对弹丸落点定位,但当弹丸落点在特定的范围时,双基阵不能准确定位。
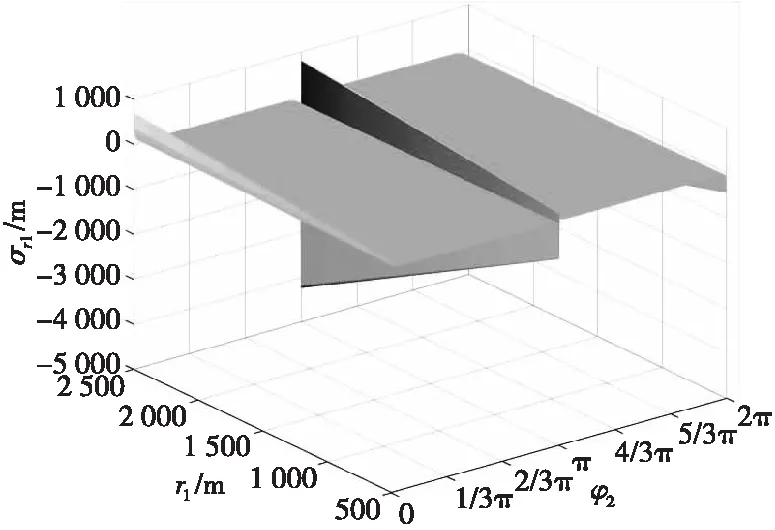
图6 双基阵测距误差分布Fig.6 Distance measurement error distribution of double base array

表1 双基阵误差
2 混合阵列定位
通过上文的分析,可知双基阵定位精度不能达到1%,不能满足弹丸落点定位要求。因此针对上文分析的问题,提出了一种基于三角阵和五元十字阵的混合阵列,通过三个中心传感器组成三角阵,当弹丸落入特殊范围时可以通过三角阵和五元十字阵组成得混合阵列对弹丸落点进行准确定位。
2.1 混合阵列定位模型
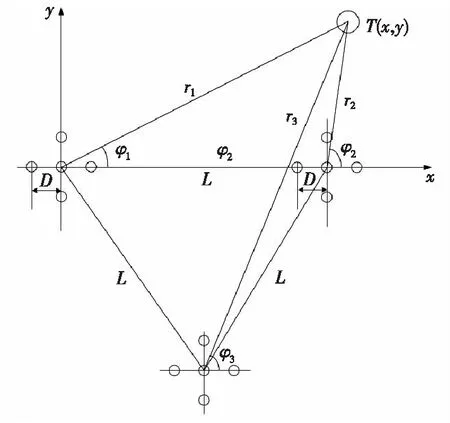
图7 混合阵列模型Fig.7 Hybrid array model
第一基阵与第二基阵不变,相距L,第三基阵的中心传感器与第一、第二基阵中心传感器组成边长为L的正三角形。第三基阵传感器间距为D,与前两个基阵组成三角阵,弥补了某些范围内无法准确定位弹丸落点的缺点。
由三角阵原理得:
(11)
结合式(11)以及图7的几何关系,带入方位角可得:
(12)
合并式(12)可得:
(13)
通过观察图7可得:
(14)
由式(14)得混合阵列对弹丸落点的预测坐标为:
(15)
2.2 误差分析
混合阵列是由三个五元十字阵列组合而成,误差分析与单、双基阵类似,不同的是要将三个五元十字阵列的中心传感器组成三角阵,通过两种阵列组合来实现对弹丸落点的全域定位。设定声速c=343.6 m/s,传感器间距D=9 m,στ=50 μs,两基阵中心传感器间距L=30 m。
通过误差传播理论可知,测距的标准差为:
(16)
3 仿真试验
通过上述分析,混合阵列对于弹丸靶场内全域定位有较高的精度。因此模仿靶场真实发射弹丸,对落点进行定位,并与真实落点进行比较,通过比较可以得到实际位置与预测位置的相对误差,当精度达到1%时,就可以确认混合阵列可以对弹丸进行准确定位。
3.1 试验过程
设定三个基阵的传感器间距均为D=9 m,各个基阵στ=50 μs,中心传感器间距L=30 m,声速c=343.6 m/s,设定一些落点。为了模仿真实靶场发射弹丸,炸点距离第一基阵中心传感器距离范围在500~2 500 m之间。
图8为模拟靶场真实弹丸发射的落点(*为落点)。通过对一些特殊区域以及边缘地的落点定位可以更加准确的检测混合阵列对于弹丸落点定位是否准确。
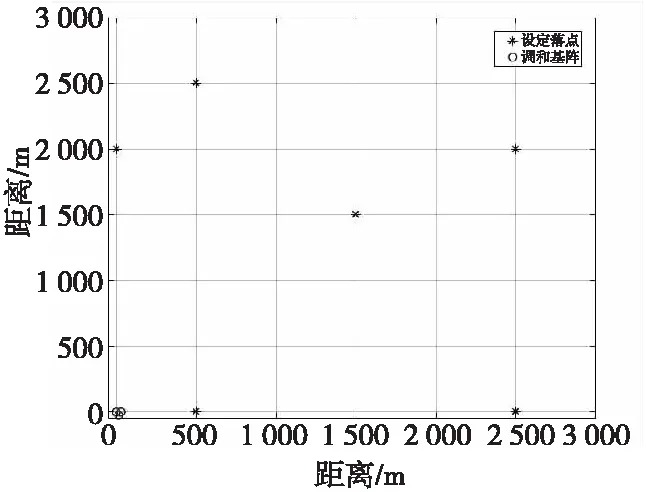
图8 模拟弹丸落点位置Fig.8 Simulate the location of the impact point of the projectile
3.2 试验结果分析
根据上述试验,可以得到每个边缘传感器与各自基阵中心传感器接收到信号的时间差,根据上文推算式(14)、式(15),可以计算出弹丸落点的位置,与模拟设定的落点进行比较,即得到了落点定位的误差值。通过混合阵列定位落点坐标如表2所示。
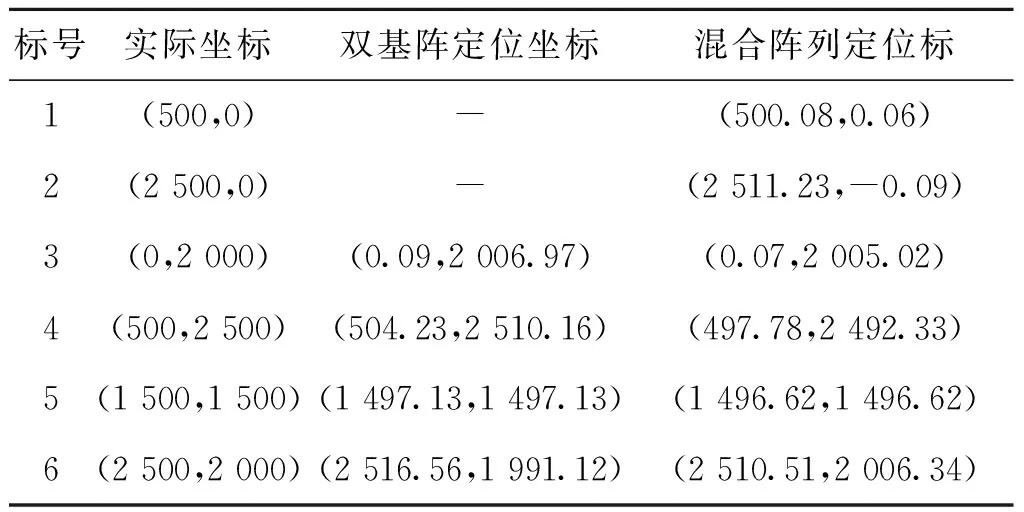
表2 各个落点坐标
通过表2可以看出,双基阵在φ2=(5°,175°)时定位精度与混合阵列相近,但是无法对φ2=0°附近区域进行定位,落点定位距离如图9所示。
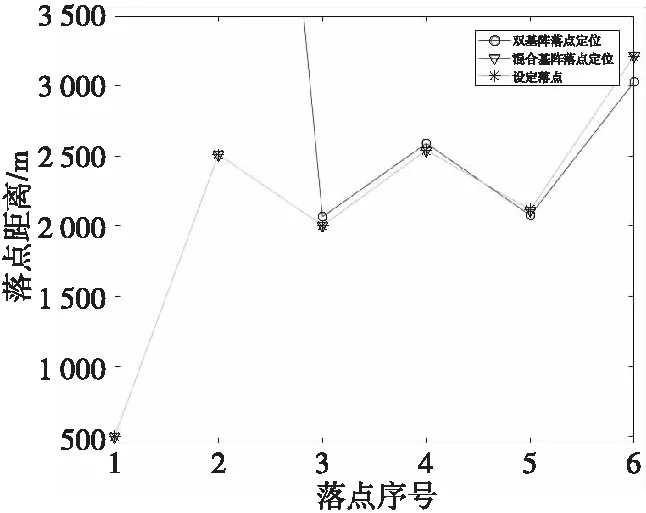
图9 两种基阵落点距离对比图Fig.9 Comparison of landing point distance between two kinds of array
通过表2可得模拟落点的距离、方位角以及混合阵列定位落点的距离和方位角,以此来求出距离以及方位角误差,如表3所示。

表3 混合阵列距离以及方位角误差
通过表3得出,落点在φ2=(-5°,5°)∪(175°,185°)时,距离误差还是比较大,但方位角在φ2=(5°,175°)误差可以达到精度要求。随着方位角向90°靠近时,方位角误差逐渐变小。通过分析可以得出,混合阵列确实解决了五元十字双基阵对于特殊区域内定位不准确的问题。
但是表中数据均是在理想环境下进行仿真试验得到的,考虑到在真实靶场发射弹丸时风速、温度、湿度以及气压对弹丸落地时声波传输的影响,误差会有一定的变化。
4 结论
本文提出了基于三个五元十字阵列组成三角形混合阵列的定位方法。该方法通过将三个五元十字阵列的中心传感器放置成为三角形阵列,以此组成混合阵列对弹丸落点定位,解决了五元十字单基阵定位精度低、双基阵对于特殊范围落点定位误差大的问题。理论推导以及理想环境下仿真试验结果表明,混合阵列对弹丸落点的定位精度误差在1%以内,满足靶场对弹丸落点的全域定位精度要求。由于本文是在理想环境下进行的仿真试验,因此针对实际靶场存在风速、温度、湿度以及气压等影响因素的定位算法还有待进一步研究。
