基于改进深度置信网络的故障诊断方法

陈子兆，矫文成，孙慧贤，李月武

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

故障诊断[1]是指在系统运行过程中，通过各种监测手段判别其工作是否正常，分析指出系统当前所处的状态，便于管理人员维修的一种技术诊断方法分为基于图论的方法[2]、基于专家系统的方法[3]、基于解析模型的方法[4]、基于数据驱动的方法[5]等。基于深度置信网络的故障诊断方法便是基于数据驱动方法中较为常用的一种。

深度置信网络(deep belief network)是一种具有高维数据训练能力的多层神经网络模型[6]。其通过训练多层限制波尔茨曼机(restricted boltzmann machine)对输入数据特征进行学习和识别，已成功应用于文本检测[7]、序列预测[8]、情感分析[9]等领域。在故障诊断[10]领域，基于深度置信网络的故障诊断方法也已经在模拟电路[11]、机械轴承[12]、风力电机[13]等方向展露风采。美中不足的是，该故障诊断方法仍存在着诸多关键问题亟待解决，其一是深度置信网络(DBN)出现过拟合后，导致故障诊断的准确率下降的问题，目前较好的解决方法是Hinton教授提出dropout策略[14-15]和添加稀疏正则项[16]策略；其二是训练小样本数据时，网络模型训练不充分导致准确率低的问题，现阶段主要有迁移学习、强化特征提取、重复训练数据集、增加数据集数据量等解决方案。

迁移学习也称为归纳学习，是将某个领域上学习到的知识应用于不同但相关的领域中的一种学习策略，文献[17—19]中便成功将迁移学习应用于小样本数据集上。但是由于无法确定迁移学习中原域和目标域的界限，所以迁移学习在故障诊断中的应用也十分有限。在强化特征提取的解决方案中，文献[20]受神经科学启发，在深度置信网络中添加一层胶质细胞层，强化相邻的隐藏层神经元的激活概率，从而优化学习过程中的关联性和特征提取能力。

针对深度置信网络对小样本故障数据集故障诊断时准确率低的问题，本文提出了基于改进深度置信网络的故障诊断方案。

1 原理介绍

1.1 深度置信网络

受限玻尔兹曼机(RBM)作为深度置信网络模型的基本单位，是由可视层v和隐藏层h构成的双层神经网络。类似于热动力学，其能量函数定义为：

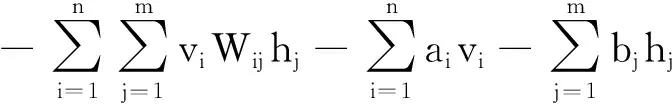
(1)

式(1)中，θ=[Wij,ai,bj]分别表示可视层与隐藏层之间网络权重、可视层偏置和隐藏层偏置，n为可视层节点数，m为隐藏层节点数。

限制玻尔兹曼机的本质是一种概率生成模型，可见层与隐藏层的联合概率分布和可见层的概率分布可表示为：

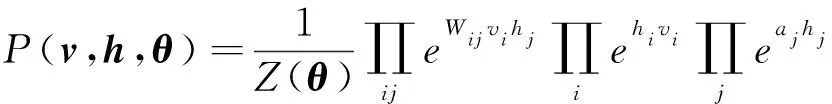
(2)

由此可以推导出隐藏节点的激活概率与可视节点重构激活概率分别为：

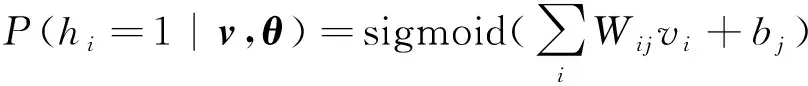
(3)

而传统的深度置信网络模型(图1)是由多层限制波尔茨曼机堆叠构成的。其在训练过程中采用了对比散度(CD)算法、贪婪学习算法、梯度下降算法(GD)等方法，训练目标是使误差函数最小。深度置信网络训练的本质就是求取最大似然概率的过程。

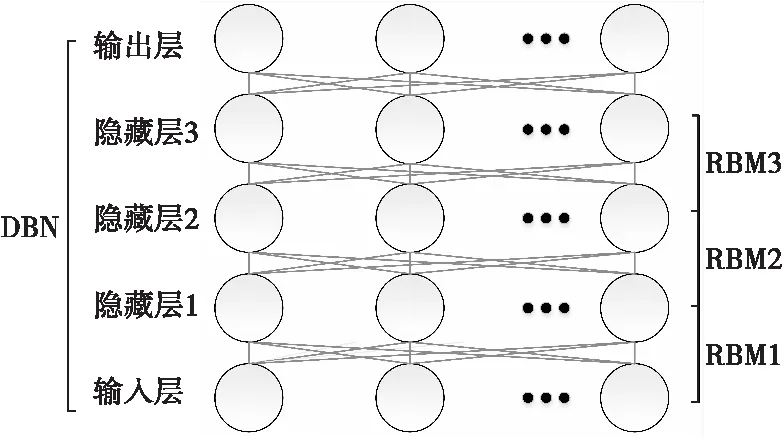
图1 DBN(3 hidden layer)结构模型图Fig.1 Structural model of DBN(3 hidden layer)

1.2 自适应谐振神经网络

自适应谐振(adaptive resonance theory)神经网络是一种无监督学习网络模型，在学习无标签数据方面具有较大的灵活性。自适应谐振(ART Ⅰ)神经网络模型如图2所示，其中比较层C负责对匹配程度与参考阈值进行比较；识别层R依据比较层的比较结果做出对应的操作，复位信号Reset、逻辑控制信号G1和G2作为神经网络的控制信号。

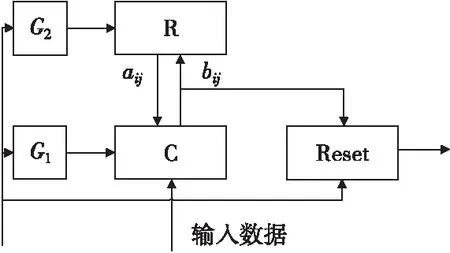
图2 ART Ⅰ结构模型图Fig.2 Structural model of ART Ⅰ

自适应谐振神经网络训练步骤可以分为匹配阶段、比较阶段、搜索阶段和学习阶段四个阶段，具体训练流程如下：

1) 匹配阶段

当输入数据X通过比较层C前向传递至识别层R时，与识别层R神经元前向权值bij进行匹配度计算：

(4)

选择具有最大匹配度的竞争获胜神经元：

(5)

2) 比较阶段

使得识别层R中获胜的神经元j激活，将其相连的反向权值aij与该输入数据X进行相似度计算：

(6)

因为输入数据X为二进制数据，N0实际表示获胜神经元的代表向量与输入模式向量之间向量同为1的次数。计输入模式向量中的非零个数为N1。设定门限阈值ρ，如果两者比值大于ρ则进入学习阶段，否则进入搜索阶段。

3) 搜索阶段

网络进入搜索阶段，使得竞争获胜的神经元持续受到抑制，并且重复匹配阶段和比较阶段，直至大于门限阈值ρ。如果所有神经元都无法满足要求，则在网络中增加一个神经元并用该输入模式向量作为该神经元的代表向量，然后进入匹配阶段。

4) 学习阶段

学习阶段主要是对获胜神经元的权值向量进行调整，使得再次出现该模式相似的输入数据时获得更大的共振和相似度。修改反向权值aij和前向权值bij公式如下：

(7)

1.3 改进ART-DBN模型的探讨与分析

自适应神经网络在学习无标签数据方面具有极大的灵活性。其通过强化特定神经元的连接权值，使得网络学习过程中具有相似特征的数据聚成一类，达到对无标签数据分类的目的。深度置信网络在学习过程中，通过逐层激活神经元，提取数据深层特征，从而对标签数据进行学习和无标签数据进行识别。当面对相同或相似输入数据时，因为具有相似的有效特征，各隐藏层层激活的神经元应当大致相同。

受到两种模型的启发，本文尝试将自适应谐振神经网络模型与深度置信网络模型相结合，将自适应谐振神经网络的训练过程与深度置信网络训练过程相结合，提出了一种改进的网络模型ART-DBN，通过利用自适应谐振神经网络对无标签数据的学习和分类优势，强化深度置信网络隐藏层中相关神经元节点的激活概率，进一步强化深度置信网络的特征提取和分类能力，最终达到提升深度置信网络分类准确率，改善网络训练效果的目的。

网络模型整体设计的思路是对相似度较大且差异度大的隐藏层神经元进行权值强化，使得其相似度进一步增大而差异度减少，从而强化对数据特征的提取能力；对相似度较大而差异度较小的隐藏层神经元，因为其激活概率较大且模式代表向量与输入模式向量类型相似，故而跳过对其权值的调整。

同时为了避免特征向量全1或者全0时出现差异度全局过小而陷入死循环，首先应当对初始化特征代表向量进行0或1的随机赋值；再者考虑到输入数据与权值参数的维度和度量上不一致，在相似度度量指标上选取用余弦距离替代欧式距离；最后因为以匹配度为调整指标的网络模型中，权值参数在调整过程中会使得相似程度和匹配程度不断增大，最终使得多次权值参数的更新只是针对同一个或几个神经元，反而导致准确率极度下降，所以我们抛弃了匹配度而选择差异度作为调整指标，以期对更多的神经元进行优化。

综上所述，改进网络模型的RBM结构如图3所示，在每一层RBM中添加了一层由星形表示的ART层，ART层由与隐藏层节点数相同的ART神经元组成，ART神经元分别与对应的隐藏层节点相连，与可视层神经元节点全连接。对此，符合要求的隐藏层节点便可通过ART层影响整个RBM，进而影响由ART-RBM堆叠构成的ART-DBN。

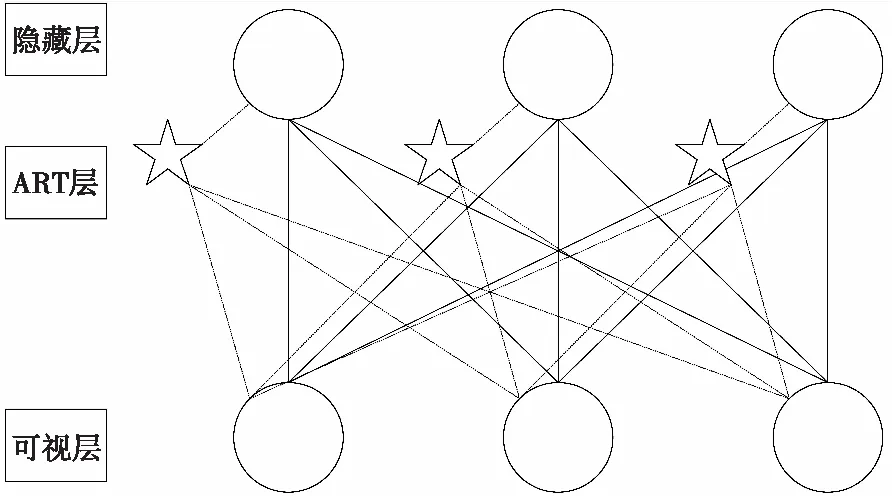
图3 ART-RBM结构模型图Fig.3 Structural model of ART-RBM

2 基于改进模型的故障诊断方法

2.1 改进模型的故障诊断方法

深度置信网络作为一种基于数据驱动的故障诊断方法，能够自动从复杂的原始故障数据分布中提取有效的特征向量，通过自带的Softmax分类器对故障类型进行分类诊断。基于数据驱动的故障诊断方法需要在庞大的故障数据支持下才能较好地完成诊断任务，但是在实际应用中，因为设备发生故障的几率微小，而发生故障时因为设备损坏又难以获取数据等原因，导致能够采集得到的故障数据极其稀少，极大程度地影响着故障诊断结果的准确率。因此本文提出了一种基于改进深度置信网络模型的故障诊断方法，图4直观地表示出基于传统深度置信网络的故障诊断方法和基于改进深度置信网络的故障诊断方法的区别。

图4 两种故障诊断方法的对比Fig.4 Comparison of two fault diagnosis methods

与基于传统模型的故障诊断方法相比，改进方法将传统的DBN模型替换为改进的ART-DBN网络模型，同时使用改进的训练规则对整个改进ART-DBN模型进行训练调优。待改进模型训练完成后，以优化后的权值参数和网络结构对输入的原始故障数据进行特征提取、分类识别，完成对故障类型的识别诊断。

2.2 ART-RBM训练规则

传统的DBN采用一步对比散度(CD-1)算法训练RBM模型，在此我们仍遵循Hinton教授在文献[21]给出训练RBM的相关建议，同时结合ART神经网络的训练规则，提出ART-RBM的训练规则。

改进的ART-RBM训练规则如下：

步骤1 输入训练数据v1，计算隐藏层激活状态h1：

h1←sigmoid(Wijv1+bj)

对隐藏层神经元赋值0或1：

ifh1> 0到1之间随机数

thenh1= 1

elseh1= 0

依据CD-1算法重构可视层神经元：

v2←sigmoid(Wijh1+ai)

对隐藏层神经元赋值0或1：

ifv2> 0到1之间随机数

thenv2= 1

elsev2= 0

再次计算隐藏层激活概率h2：

h2←sigmoid(Wijv2+bj)

步骤2 根据CD-1算法更新网络参数：

Wij←Wij+Wv

ai←ai+av

bj←bj+bv

步骤3 计算输入数据与隐藏层神经元之间的相似度：

选取相似度最优的隐藏层神经元：

Sk←Fmax(Scos(j))

步骤4 选取最优隐藏层神经元的特征代表向量与重构后的输入向量v2计算差异度：

对满足不同条件差异度的神经元采取不同的措施：

ifσ>ρ

thenWik←Wik+kασWik

Wi,j≠k←Wi,j≠k-kασWik

dik←dikv2

else抛弃最优神经元，重新搜索

步骤5 重复迭代直至达到最大网路迭代次数epoch。

2.3 ART-DBN训练规则及其故障诊断应用

作为构成ART-DBN模型的基础单元，改进的ART-DBN训练规则与传统DBN训练规则的流程相似，ART-DBN也是采用贪婪学习算法的方法逐层训练ART-RBM，而后采用反向传播算法对ART-DBN模型全局调优。不同的是将传统的DBN网络中针对RBM预训练步骤更新为针对ART-RBM的预训练步骤。故而基于ART-DBN网络模型的故障诊断方法如图5所示。

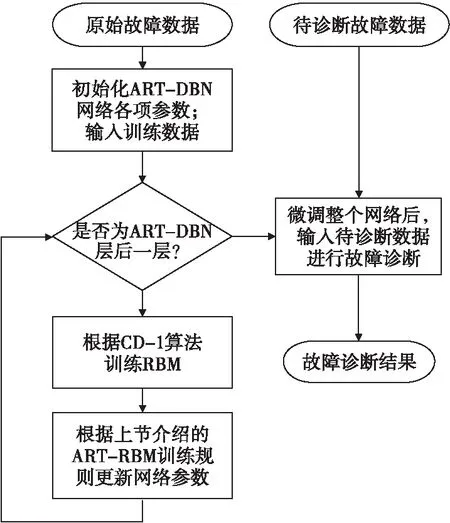
图5 基于ART-DBN网络的故障诊断图Fig.5 Fault diagnosis based on ART-DBN network

ART-DBN网络模型通过对原始故障数据的训练和学习，完成对已知故障类别的识别，然后将待诊断的故障数据输入网络模型中，由模型提取待诊断故障数据的特征向量并进行识别诊断，完成对待诊断故障数据的诊断工作。

3 实验分析

本章首先在三种网络公开数据集上，将提出的ART-DBN网络模型与传统的神经网络模型、文献[17]所提出的改进网络模型(以下简称SP-DBN)等进行对比实验，以观察提出的ART-DBN网络模型的性能优劣；然后将所提出的网络应用于实际的小样本数据集故障诊断以检验模型的实时性和实用性。

3.1 参数选取

实验中设定的各项基本参数为：学习率α为0.01，稀疏正则化参数λ为0.000 5，冲量p为0，批训练量batchsizes在ORL数据集下为30，在MNIST和CIFAR-10数据集下为100，网络搜索次数epoch在ORL数据集下为1 000次，在MNIST和CIFAR-10数据集下为3 000次。实验开发环境为Matlab R2015b。

3.2 特征可视化实验

本节首先对所提出的ART-DBN网络、传统的DBN网络和稀疏DBN网络三种模型在ORL数据集上进行可视化操作，以检验三种模型的特征提取能力。实验一中，三种模型均选取可视层节点数为784和隐藏层节点数为100的RBM网络结构，模型学习得到的可视化图形如图6所示。

图6 特征可视化图Fig.6 Feature visualization

从图6可以看出，三类网络结构与原图相比，传统的DBN网络模型对特征提取较差，特征点分布的杂乱无章，无法人眼识别出所提取的内容；稀疏的DBN网络模型对特征提取较好，围绕着原图形的亮点出现有规则的分布，人眼对少数图片能识别出所提取的内容；ART-DBN网络模型对特征提取最好，特征点基本与原图形相吻合，人眼大致能识别出所提取的内容。

由此可以得出所提出的ART-DBN网络模型通过添加ART层强化某一种类型的神经元，使得网络模型对某一类图形特征提取的能力显著提高，能够较好地学习输入图片中所包含的特征数据并且能较完整地还原出原图形。

3.3 MNIST数据集下对比实验

MNIST数据集包含10组，每组7 000张，共70 000张手写黑白照片。本文选取其中每组6 000张照片，共60 000张照片作为训练数据集用以训练网络，选取余下的每组1 000张照片，共10 000张照片作为测试数据集用以测试网络性能。

在MNSIT数据集下，本小节进行了两组实验以验证ART-DBN网络模型的优越性。实验二为双隐藏层数200，100条件下，不同差异度取值的准确率比较，实验结果如图7所示。实验三为固定差异度条件下，不同双隐藏层节点数的准确率比较，实验结果如表1所示。

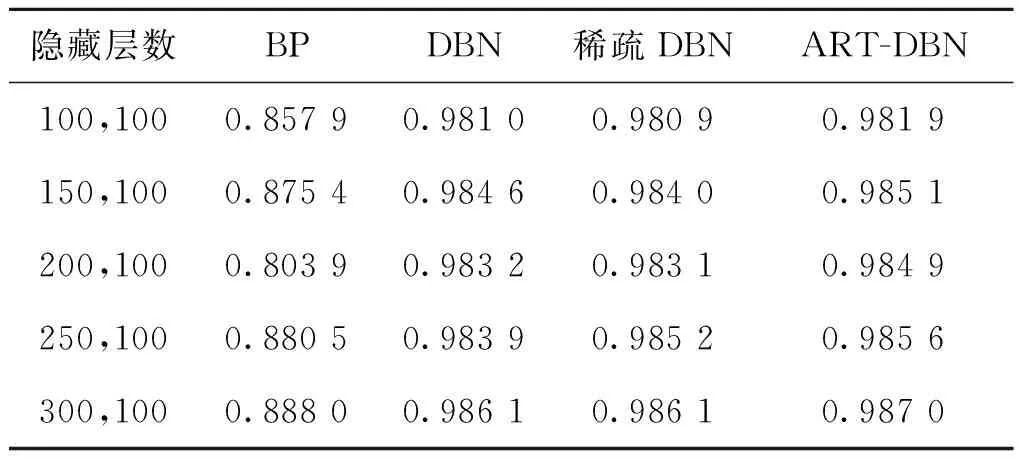
表1 MNIST数据集上四种模型的准确度

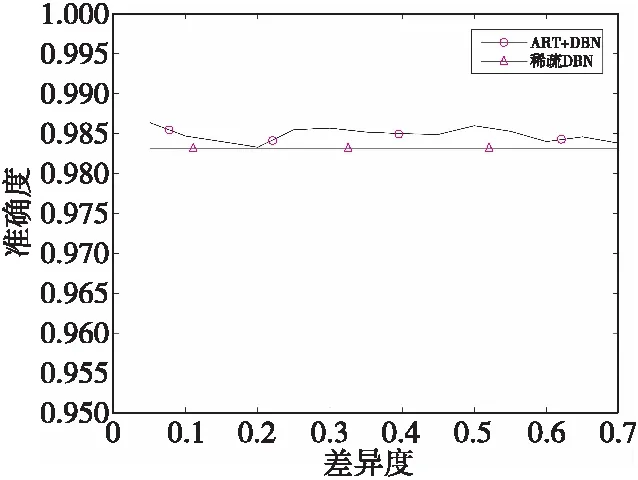
图7 MNIST数据集上差异度变化图Fig.7 Different degrees on MNIST

从图7可以看出，本文提出的ART-DBN网络模型的准确率始终高于稀疏的DBN网络模型的准确率，说明了MNIST数据集下改进的DBN较稀疏DBN网络更加优异，同时可以看出ART-DBN网络模型在200，100双隐藏层条件下，准确率处于98%左右。选取差异度σ为0.45，具有一定的代表性。

表1为ART-DBN网络模型与BP、传统DBN、稀疏DBN三种网络模型不同隐藏层数条件下的对比实验，其中ART-DBN网络模型中的差异度σ根据实验四赋值为0.45。从表1中可以看出，BP网络模型表现最差，稀疏DBN与传统DBN网络模型其次，ART-DBN网络模型表现更为优异。实验证明了BP神经网络对于大数据量的学习与分类已不相适应，同时在MNIST数据集上，ART-DBN网络模型较传统的DBN网络模型和稀疏的DBN网络模型准确率更高。但是由于传统的DBN网络模型识别准确率已经达到98%，提升准确率的幅度不是很大。

3.4 CIFAR-10数据集下对比实验

CIFAR-10数据集包含10组，每组6 000张，共60 000张彩色图像。本文提取所有彩色图像RGB三色作为特征数据，可视层神经元节点数为3×1 024个。本文选取其中每组5 000张图片，共50 000张图片作为训练数据集用以训练网络，选取余下的每组1 000张图片，共10 000张图片作为测试数据集用以测试网络性能。

在CIFAR-10数据集下，本小节进行了两组实验以验证ART-DBN网络模型的优越性。实验四为双隐藏层数100，100条件下，不同差异度取值的准确率比较，实验结果如图8所示。实验五为固定差异度条件下，不同双隐藏层节点数的准确率比较，实验结果如表2所示。

从图8可以看出，在双隐藏层数为100，100的条件下，变化差异度的取值，ART-DBN网络模型较稀疏DBN网络模型表现略有下降，准确率略有降低。分析原因可能是由于隐藏层数较少，网络参数的更新调整使得网络出现的正常范围内波动。因为CIFAR-10数据集的可视层节点数为3 072，较一般数据集偏多，为此选取差异度为0.35，降低差异度的取值是为了使得ART层更易满足差异度阈值，从而极大程度对神经元的权值更新调整。

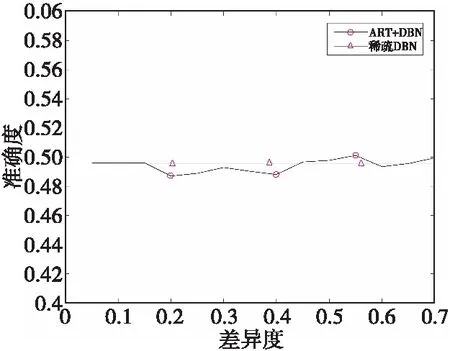
图8 CIFAR-10数据集上差异度变化图Fig.8 Different degrees on CIFAR-10

表2为ART-DBN网络模型与BP、传统DBN、稀疏DBN三种网络模型不同隐藏层数条件下的对比实验结果，其中ART-DBN网络模型中的差异度σ根据实验四赋值为0.35。从表2中可以看出，BP网络模型表现最差，稀疏DBN与传统DBN网络模型其次，ART-DBN网络模型表现更为优异。因为对CIFAR-10数据集的学习，一般的深度神经网络学习后准确率为50%左右，而BP神经网络属于浅层神经网络，准确率有所下降。实验证明了通过添加ART层的改进神经网络较传统DBN和稀疏DBN在准确率上有所改善。

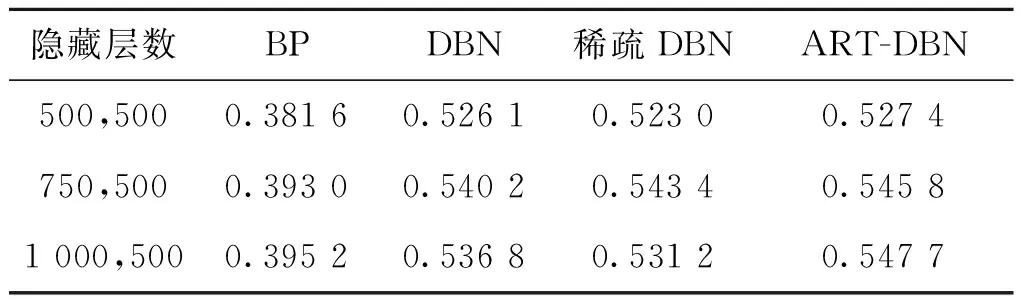
表2 CIFAR-10数据集上四种模型的准确度

3.5 小样本故障数据集的对比实验

小样本故障数据集是对军内某通信控制装备的正常状态和六种故障状态下的时域波形图采样1 000点并均值归一化后得到的数据集，包含7组，每组200～1 000组数据不等，共计4 042组。本文选取每组80%左右数据，共3 470组数据作为训练数据集用以训练网络，选取余下的数据，共572组数据作为测试数据集用以测试网络性能。

在武器装备故障数据集下，本小节进行了两组实验以验证ART-DBN网络模型的优越性。实验六为固定差异度条件下，不同双隐藏层节点数的准确率比较，实验结果如表3所示。实验七为固定网络参数条件下，各网络模型对故障数据集分类准确率上限的测试，实验结果如表4所示。

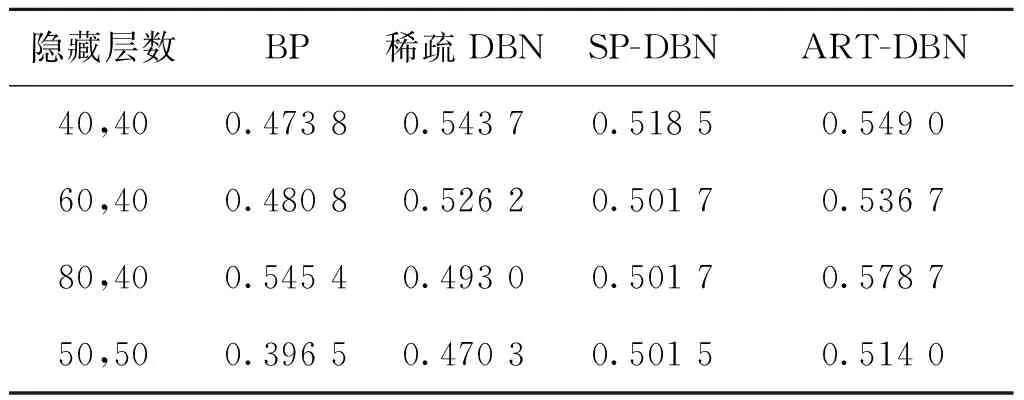
表3 故障数据集上四种模型的准确度

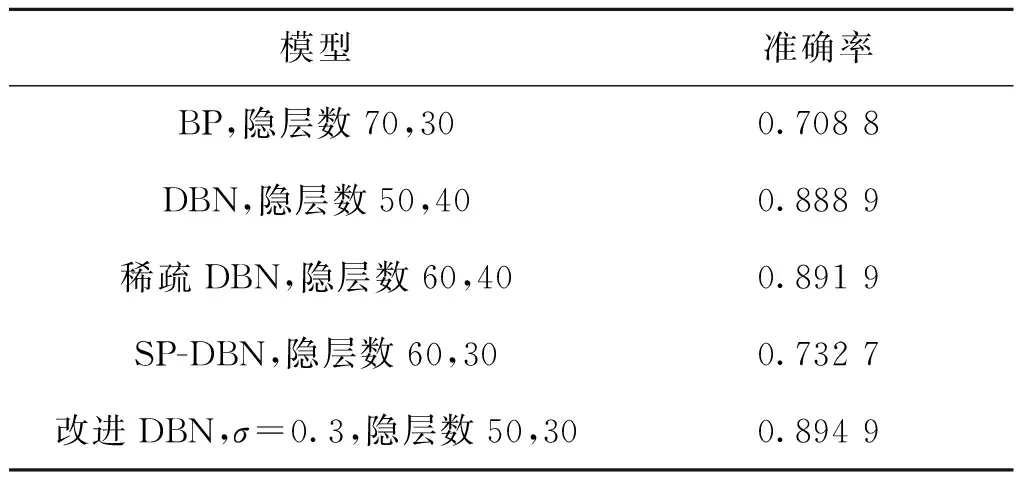
表4 故障数据集上准确度的上限

表3为ART-DBN网络模型与BP、稀疏DBN、SP-DBN三种网络模型不同隐藏层数条件下的对比实验结果，其中ART-DBN网络模型中差异度σ赋值为0.7。从表3中可以看出，本文改进的DBN模型对装备故障数据集的学习和分类能力强过传统的BP、DBN网络模型。但是由于本文未对时域波形图采取如小波变化等方法的特征提取，所以准确较低。

表4为装备故障数据集下，五种网络模型准确率上限的测试实验结果。通过反复实验尝试，得出改进DBN网络模型的准确率上限为90%左右，较其他四种网络模型有一定改善，在武器装备故障诊断领域的表现优于其他四种网络模型。

3.6 小样本故障诊断的性能分析

为了更好地评价改进的方案，我们引入准确率、召回率、精确率等指标全面衡量其性能优劣。如果以P(Positive)和N(Negative)分别代表真实的正常数据和故障数据的数量，以T(Ture)和F(False)代表模型判断正确和错误的数量，那么TP则表示模型判断为正常数据，实际也是正常数据的数量；TN则表示模型判断为故障数据，实际也是故障数据的数量；FP则表示模型判断为故障数据，但实际却是正常数据的数量；FN则表示模型判断为正常数据，但实际也是故障数据的数量。需要说明的是上述三种指标适用于基于二分类的机器学习方法，但在此处我们将所有的不同类型的故障数据统称为故障数据，因此该指标参数同样适用于本实验。

由此即可定义：

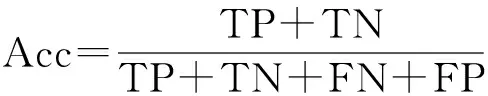
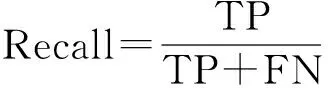
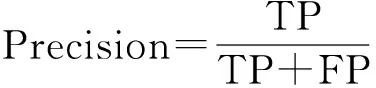
实验八为对上述三种模型在隐藏层为100-40条件下各识别结果的统计，结果如表5。

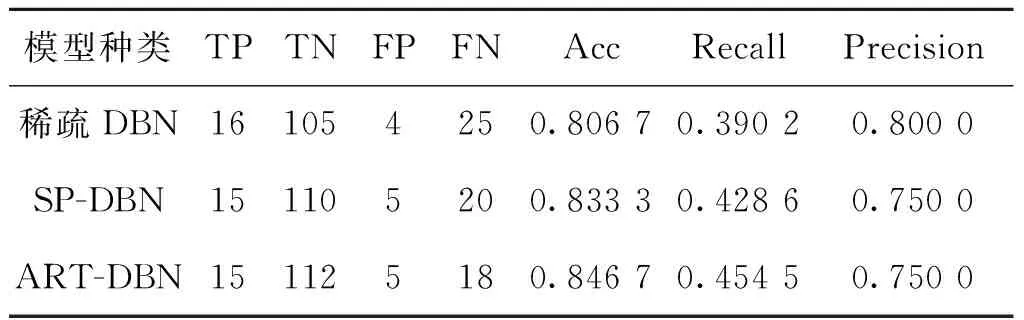
表5 故障数据集上各模型指标对比表

从表5可以得知：改进模型的召回率为45.45%，精确率为75%。分别与其他两种模型对比发现，改进模型在召回率上表现最好，说明对于正常样本，改进模型能起到很好的识别作用，同时计算得出在所有故障样本中，改进模型识别为故障样本的比例为95.73%，漏警概率为54.55%，在三种模型中表现最好。通过实验可以证明小样本数据集的故障诊断，改进模型性能优于其他两种模型，一定程度上解决了小样本故障数据集下网络训练效果差的问题。

3.7 小样本故障诊断的训练时间分析

不可否认的是通过在网络中额外加入了一层用于强化特征提取的ART层，会导致网络训练的时间额外增加，故此又进行了一组实验以测算改进模型用于故障诊断所耗费的时间。实验九为在通信控制设备故障数据条件下的网络训练耗时测算实验，实验结果如表6所示。

从表6可以看出改进网络模型较传统模型训练时间延长了2～3倍，但对于故障诊断领域，适当牺牲训练时长而换取更好的训练效果和更高的分类准确率是值得的。

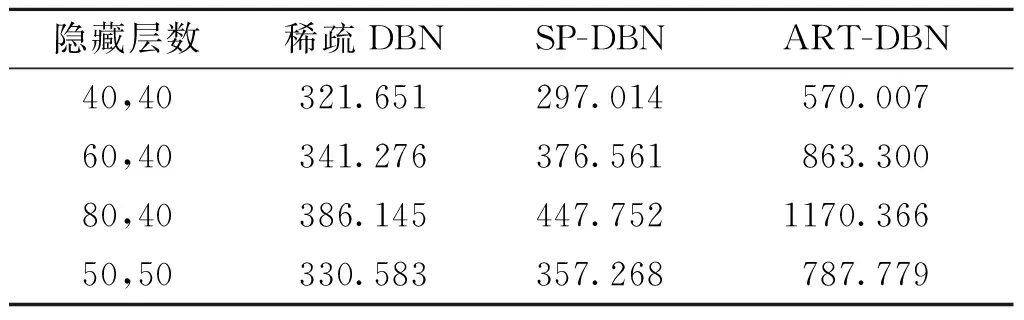
表6 故障数据集上的训练耗时

4 结论

本文提出了基于改进深度置信网络的故障诊断方法。该方法通过将深度置信网络与自适应谐振神经网络结合，优化网络特征提取的能力，提升网络学习和分类能力以减少网络训练对数据的依赖程度，利用ORL，MNIST和CIFAR-10等网络公开数据集测试改进的深度置信网络模型的性能，并将改进网络模型应用于小样本故障数据集上。实验验证结果表明，较基于传统网络模型的故障诊断而言，基于改进模型的方法通过添加新的隐藏层，强化了模型特征提取能力，提高了故障诊断的准确率。