雷达侦察截获效能评估的马尔科夫动态修正方法

雷震烁，刘松涛，温镇铭，葛 杨

(海军大连舰艇学院信息系统系，辽宁 大连 116018)

0 引言

面对现代战场电磁环境日益复杂的严峻形势，雷达对抗效能评估技术越来越受到重视，其中雷达侦察截获效能评估是衡量系统侦察能力的重要指标。侦察截获效能评估即在对抗发生前定量估算侦察系统对雷达信号获取能力的过程[1]。传统评估一般采用建立静态模型的方式，即模型建立完成后仅通过输入参数的变化影响评估的结果，模型本身不再进行修正。

目前对于静态评估模型的研究已取得了一定进展。文献[2]通过窗口函数结合概率论分析了系统前端截获概率，得出捷变频雷达前端截获概率公式。文献[3]通过构建评估指标数学模型并分析雷达侦察性能，形成了作战效能评估理论框架。文献[4]针对导引头雷达捷变频信号窄带搜索问题，提出均匀分布与高斯分布两种侦察方式模型并进行效能评估。文献[5]对相控阵雷达波束及扫描特征分析，建立了相控阵侦察截获概率模型。文献[6]建立了自适应对抗模型结合机器学习算法实现雷达效能评估。文献[7]以雷达系统自身的数据及战时环境作为评估参数，得出侦察截获效能预期评估方法。然而，考虑到战场数据反馈速度的不断提高和复盘技术的持续优化，在对抗中会实时产生许多有价值的数据，这些实时数据在传统雷达侦察截获效能评估时并没有得到有效利用。本文针对此问题，提出了雷达侦察截获效能评估的马尔科夫动态修正方法。

1 传统雷达侦察截获效能评估

对雷达信号的侦察主要分为发现和识别两个方面，前者包括信号的搜索与检测，后者包括信号的分析和辨识[8]。传统雷达侦察截获效能评估主要针对发现雷达信号的过程，选择前端截获概率作为评估指标，此处侦察系统选择定向天线。

在侦察系统与被侦察雷达(下文简称雷达)空域频域对准的情况下，设侦察系统在雷达所在空域频域驻留时长为t，侦察系统回访时间间隔为T，雷达主瓣及其有效旁瓣在侦察系统方向上的单次照射时长为τ，雷达照射时间间隔为S。对于固定周期扫描雷达，τ和S为固定值，对于随机扫描雷达，τ和S为随机值。将侦察系统驻留时长t与雷达单次照射时长τ的重叠时间作为侦察系统有效侦收时长，如图1所示。当有效侦收时长大于最短截获时长λ时，视为侦察系统成功截获雷达信号。

传统评估模型选取t，T，λ，τ作为评估参数，以截获概率作为指标进行雷达侦察截获效能er评估，表示为[7]：

(1)

式(1)中，P为侦察系统截获固定周期扫描雷达概率，当τ>T+2λ时，雷达单次照射时长覆盖侦察系统搜索周期，侦察系统一定可以截获雷达信号，即P=1。当τ≤T+2λ时需要根据侦察系统截获信号条件计算，表示为：

(2)

E(P)为侦察系统截获随机扫描雷达概率的数学期望，表示为：

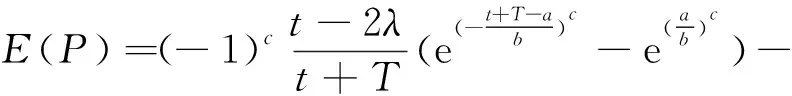
(3)

式(3)中，a，b，c为Weibull分布参数，通过Weibull分布函数对随机值τ进行拟合。

评估过程中t，T，λ可由侦察系统直接获得，τ可由侦察系统积累历史数据通过数学拟合的方法推算得出，因此参数都由侦察方获得，可在对抗发生前进行效能预期评估。

2 马尔科夫动态修正方法

对雷达侦察截获效能评估的马尔科夫动态修正方法包括四个步骤：数据预处理、相关性分析、模型建立和误差分析，流程如图2所示。

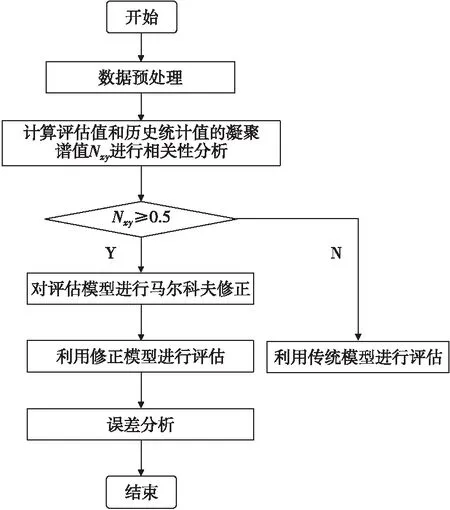
图2 马尔科夫动态修正方法Fig.2 Markov dynamic correction method

1) 数据预处理。为利用历史统计值对评估值进行修正，需要将数据维度统一，同时补全空缺数据。当空缺数据前后三个时刻都为已知数据时，用非邻均值代替空缺数据，表示为：

(4)

否则用趋势比例值代替空缺数据，表示为:

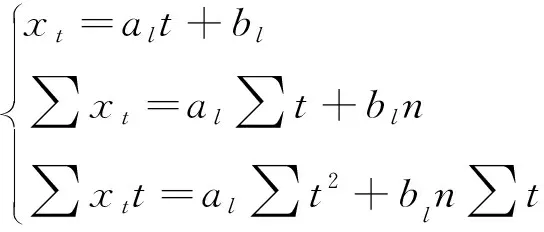
(5)

式(5)中，al，bl为拟合参数，n为时刻数，一般取3即可。

2) 相关性分析。计算评估值和历史统计值的凝聚谱值，若凝聚谱值较大，说明相关水平较高，利用历史统计值修正评估值可以提高评估准确度，详见第2.1节。

3) 模型建立。根据相关性分析结果，建立雷达侦察截获效能评估的马尔科夫修正模型，包括参数预处理、模型构造与应用和误差预测与消除，详见第2.2节。

4) 误差分析。为直观表示各评估方法的优劣，采用百分比误差eAPE、平均百分比误差eMAPE和均方差eMSE进行误差分析，误差数值越小说明评估方法越准确，表示为：

(6)

(7)

(8)

式(6)—式(8)中，pr为截获效能统计值，er为该方法截获效能评估值，g为样本点数。

2.1 评估值和历史统计值的相关性分析

凝聚谱值能描述两个数据序列的相互关系即相关性。在应用时，往往先将两个数据序列在频域上进行预处理，按不同的时间尺度选取两个数据序列中的部分数据构成两个新序列，对这两个新序列进行相关性分析计算。凝聚谱以两个数据序列X=x1，x2，…，xn，Y=y1，y2，…，yn为输入；X，Y的自相关系数Rxx，Ryy，落后相关系数Rxy，Ryx[9]分别表示为：

(9)

(10)

(11)

(12)

式中，k为落后阶数，k=0，1，…，n为数据序列的长度。

两个数据序列时间谱ch(f)，qh(f)表示为：

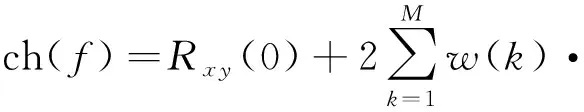
(13)

(14)

式中，f为谱频率，M=n/3为截断点数量，w(k)为权系数，表示为：

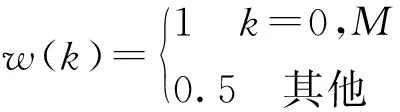
(15)

则X，Y的单谱、交叉谱表示为：

(16)

(17)

Sxy(f)=ch(f)+iqh(f)

(18)

二者凝聚谱Nxy(f)[10]表示为：

(19)

凝聚谱值越大，表明两个原数据序列的相关性越强。将其归一化后，相关性水平与凝聚谱值的对应关系如表1所示。基于此认为凝聚谱值高于0.5，即二者至少处于显著相关的程度时，适宜采用马尔科夫链动态修正方法。由于战场态势的差异，不同对抗过程中评估值与历史统计值相关性差异较大，建立模型前应进行交叉谱分析。

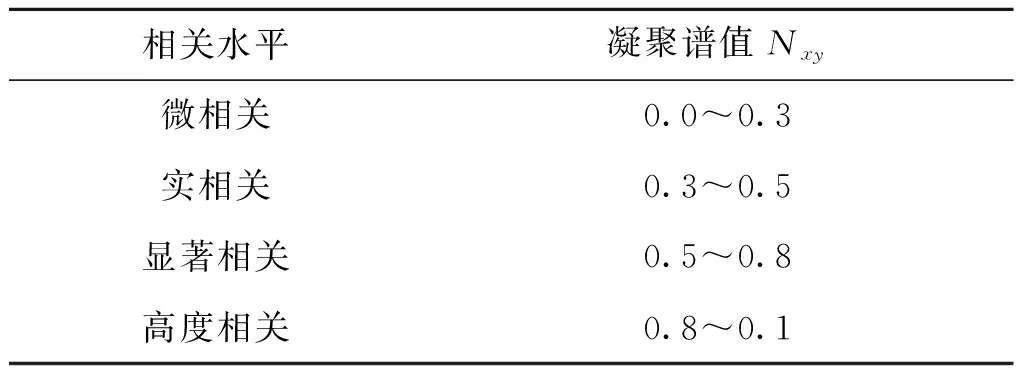
表1 相关性水平与凝聚谱值对应关系

2.2 马尔科夫动态修正模型

马尔科夫过程即序列在T时刻的状态由且仅由T-1时刻的状态决定，表示为：

Pr{XT+1=iT+1|X1=i1,X2=i2,…,XT=iT}=
Pr{XT+1=iT+1|XT=iT}

(20)

式(20)中，Pr为状态转移概率，XT为T时刻状态变量，iT为XT具体状态，XT+1为T+1时刻状态变量，iT+1为XT+1具体状态。

雷达侦察截获效能具有纵向相似性，即t时刻侦察截获效能与t-1时刻侦察截获效能关联度较高，因此历史统计值序列、评估值序列都可以视为马尔科夫状态链。为了在评估时将历史统计值因素考虑在内，构造以评估值作为主状态链、历史统计值作为辅状态链(以下简称主链和辅链)的双马尔科夫链模型，如图3所示。图中X1，X2，…，XT表示主链X状态变量；Y1，Y2，…，YT表示辅链Y状态变量；t时刻的马尔科夫修正值受传统侦察截获效能评估模型和辅链t-1时刻状态变量共同影响。

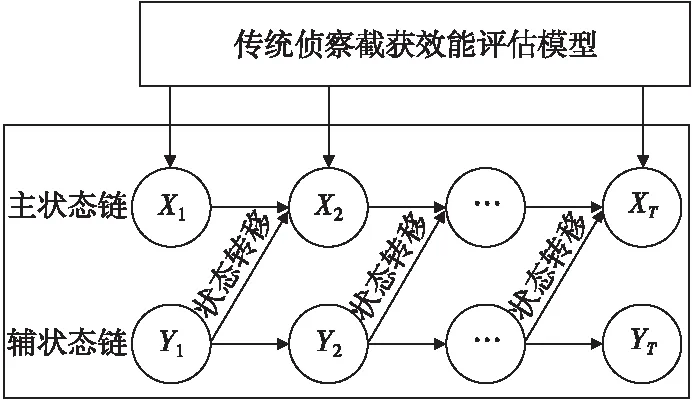
图3 双链马尔科夫过程Fig.3 Double-chainmarkov process

模型具体分解为划分状态区间、构造主链状态向量、构造辅链状态向量、构造转移概率矩阵集合、计算辅链预测值、计算主链马尔科夫修正值和误差预测消除7个步骤。以对t=i时刻侦察截获效能进行评估为例进行说明。

1) 划分状态区间。采取无监督等宽离散化方法[11]将评估值和历史统计值数值区间划分为M个子区间，映射为状态集合S。

2) 构造主链状态向量Xi。依据传统评估模型计算评估值，得到t=1，2，…，g时刻评估结果并将其离散化。Xi表示t=i时刻评估值状态，评估值所在列元素为1，其余为0。

3) 构造辅链状态向量Yi-1。依据外部系统获取历史统计值，得到t=0，1，2，…，g时刻统计值并离散化，设链头t=0时刻(即评估开始的前一时刻)历史统计值为0。本文假设t时刻外部系统可以完成对t-1时刻雷达侦察截获效能历史统计值的采集，实际中若部分时刻无法完成统计值采集，则利用前文提到的数据预处理方法进行补全空缺数据。Yi-1表示t=i-1时刻历史统计值状态，历史统计值所在列元素为1，其余为0。

4) 构造转移概率矩阵集合A。A包含A1，A2，…，AM等M个状态转移概率矩阵，其中Am表示辅链t-1时刻状态为m时，t时刻M个状态的转移概率。对辅链前一时刻处于状态m时，当前时刻状态进行数学统计，以频率表示各状态转移概率p，转移概率矩阵集合Am表示为：

(21)

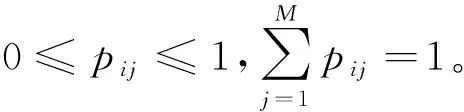
5) 计算辅链预测值hi。取各状态区间上下限平均值构建数值列向量V=[v1,v2,…,vm]进行离散还原，vj即第j个元素，表示为：

(22)

式(22)中，vmaxj为第j个区间上限，vminj为第j个区间下限。

辅链预测值hi表示为：

hi=Yi-1×AYi-1×V(i=1,2,…,g)

(23)

式(23)中，AYi-1为辅链状态为Yi-1时的状态转移概率矩阵。

6) 计算马尔科夫修正值Zi，表示为：

Zi=(1-σ)Xi+σhi

(24)

式(24)中，Xi为t=i时的评估值，σ为辅链权重参数，一般取0.5为宜。

7) 为减小模型误差，对模型进行误差预测和消除。首先进行数据回测，将t-1时刻马尔科夫修正值与t-1时刻历史统计值比较计算百分比误差eAPE；而后，划分误差状态区间并建立误差状态转移矩阵，当误差小于或等于2%时认为产生了正常误差，高于2%时认为产生严重误差，得到误差状态序列；最后，以单链马尔科夫模型预测t时刻修正值误差状态。由于雷达侦察截获效能本身的波动性较大，所以当已经连续出现两次严重误差，且对下一时刻误差预测依旧为严重时，才认为模型产生较大误差并进行消除，经误差消除后的修正值ZiN表示为：

(25)

式(25)中，eAPEN为预测百分比误差。

综上，马尔科夫动态修正模型流程如图4所示。

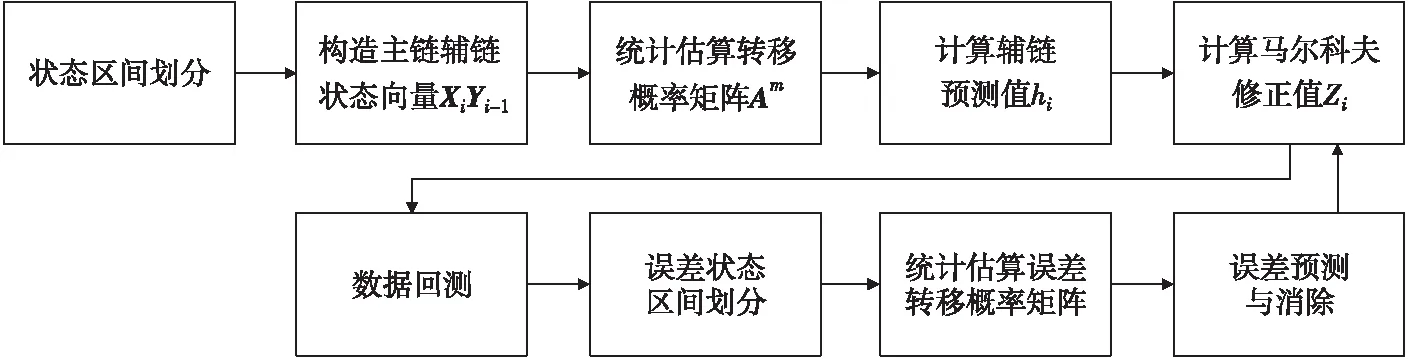
图4 马尔科夫动态修正模型Fig.4 Model of markov dynamic correction

3 仿真实验

通过仿真实验，模拟侦察系统截获雷达信号的过程。过程中利用外部系统获得截获概率历史统计值并作为实际侦察截获效能，利用传统侦察截获效能评估方法得到评估值[7]，利用本文方法得到马尔科夫修正值，对三者进行比较分析，验证本文方法准确性。共设计两个实验场景：场景一为侦察系统侦察1部雷达信号，验证单雷达情况下评估参数规律变化时，马尔科夫修正方法效能评估的准确性；场景二为侦察系统侦察16部雷达信号，验证多雷达情况下，马尔科夫修正方法综合效能评估的准确性。

3.1 单雷达侦察截获效能评估

本场景设计为侦察系统侦察1部雷达信号，当评估参数变化时，验证马尔科夫修正方法效能评估的准确性。此处变化的评估参数可选择侦察系统驻留时长t、侦察系统回访时间间隔T、雷达单次照射时长τ和最短截获时长λ中的任意一项。由于选择最短截获时长λ时，传统评估值准确性较差，可更好地体现本文方法的改进效果，故选择最短截获时长λ作为变化的评估参数，雷达选择随机扫描雷达。

仿真过程中每次实验的时间长度设定为2 000 s，侦察系统驻留时长t=97 ms，侦察系统回访时间间隔T=501 ms，雷达单次照射时长τ为随机产生的数据，通过Weibull分布进行拟合，如图5所示，雷达照射时间间隔设为指数分布，分布均值为1 020 ms。最短截获时长λ以1 ms为步长在区间[5,50] ms内递增变化。以30个样本点为周期计算侦察截获效能的统计值与传统评估方法评估值凝聚谱Nxy=0.845，属于高度相关，可以使用本文方法。

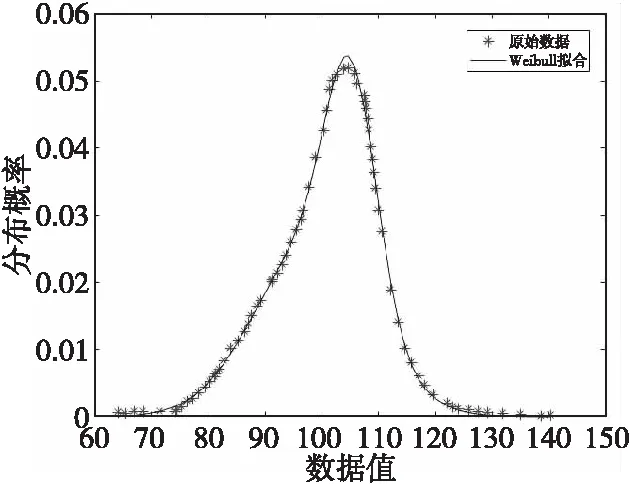
图5 原始数据概率分布与Weibull分布拟合Fig.5 Fitting of original data probability distribution and Weibull distributionn

将侦察截获效能的历史统计值、传统模型评估值和本文方法得到的马尔科夫修正值进行比较。同时引入支持向量机(SVM)评估值和神经网络评估值作为参考，训练集选取样本数的70%，SVM选取BRF径向基核函数，惩罚系数c和核函数参数g由粒子群算法优化得到，神经网络选择BP神经网络，传递函数选择tansig，中间层神经元个数设为13。所得结果以及绝对百分比误差，如图6所示。

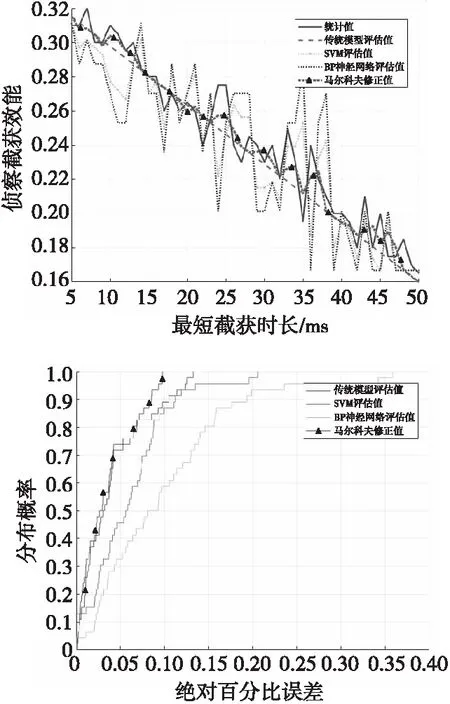
图6 单雷达侦察截获效能评估结果Fig.6 Results of interception effectiveness evaluation of single radar reconnaissance

为去除奇异值影响，计算最小百分比误差时选取样本中误差最小的90%，计算平均百分比误差和均方误差时选取全体样本。由仿真结果可知，传统模型评估值90%以上与统计值百分比误差在11.2%以内，平均百分比误差为4.0%，均方误差为1.896×10-3。SVM评估值90%以上与统计值百分比误差在12.4%以内，平均百分比误差为5.9%，均方误差为3.183×10-3。BP神经网络评估值90%以上与统计值百分比误差在19.1%以内，平均百分比误差为9.9%，均方误差为4.634×10-3。马尔科夫修正值90%以上与统计值百分比误差在7.1%以内，平均百分比误差为3.5%，均方误差为1.198×10-3。本文方法误差较小，评估效果更精确。

3.2 多雷达综合侦察截获效能评估

本场景设计为侦察系统侦察16部雷达信号时，验证马尔科夫修正方法综合效能评估的准确性。16部雷达中，4部为静止固定周期扫描雷达，4部为运动固定周期扫描雷达，4部为静止随机扫描雷达，4部为运动随机扫描雷达，如图7所示。

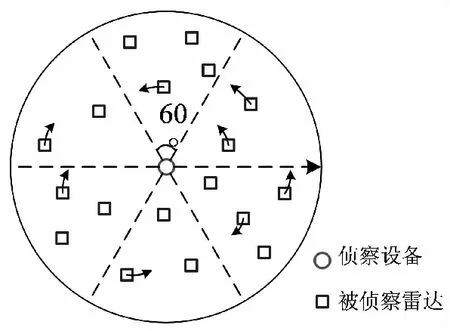
图7 多雷达综合侦察截获效能评估仿真场景Fig.7 Simulation scene of comprehensive interception effectiveness evaluation of multi-radar reconnaissance

将场景简化为二维模型，设侦察系统极坐标为(0，0)，雷达极坐标为(ri,θi)，其中ri取值范围为[150,400] km，θi取值范围为[0,360]°，运动雷达以250 m/s的速度以侦察系统为圆心顺时针或逆时针运动，雷达频点为S波段(2～4 GHz)内随机值。侦察系统空域扫描范围为360°，每个瞬时视场为60°，频域扫描范围为S波段，每个瞬时扫描频段带宽500 MHz，因此侦察系统共有24个搜索区间，对其依次进行扫描，每个驻留时长扫描其中一个区间。

仿真时间长度设定为5 000 s。侦察系统的侦察策略选择权重扫描策略，即16部雷达中有8部为一般目标权重为1，另8部为重要目标权重为2。侦察系统最短截获时长λ=5 ms；各搜索区间驻留时长t=100 ms，搜索区间中每多一个一般目标驻留时长增加100 ms，每多一个重要目标驻留时长增加200 ms；各搜索区间回访时间间隔T为其余23个区间驻留时长t的总和。固定周期扫描雷达单次照射时长τi取值范围为[10,100] ms，照射时间间隔Si=10τi；随机扫描雷达单次照射时长τ为随机产生的数据，通过Weibull分布进行拟合，照射时间间隔为指数分布，分布均值为500 ms。以30个样本点为周期计算侦察截获效能统计值与传统评估方法评估值凝聚谱Nxy=0.752，属于显著相关，可以使用本文方法。

综合侦察截获效能的统计值Pall和评估值eall由各雷达侦察截获效能组合而成，表示为：

(26)

(27)

式(26)、式(27)中，K为总雷达个数，ncap为第i部雷达被截获次数，Nsend为第i部雷达照射雷达次数，wi为第i部雷达权重系数，W为总权重系数，er为第i部雷达效能评估值。

将雷达综合侦察截获效能的历史统计值、传统模型评估值和本文方法得到的马尔科夫修正值进行比较，由于实验一中SVM，BP神经网络方法误差较大，此处不再引入进行对比。所得结果以及绝对百分比误差，如图8所示。

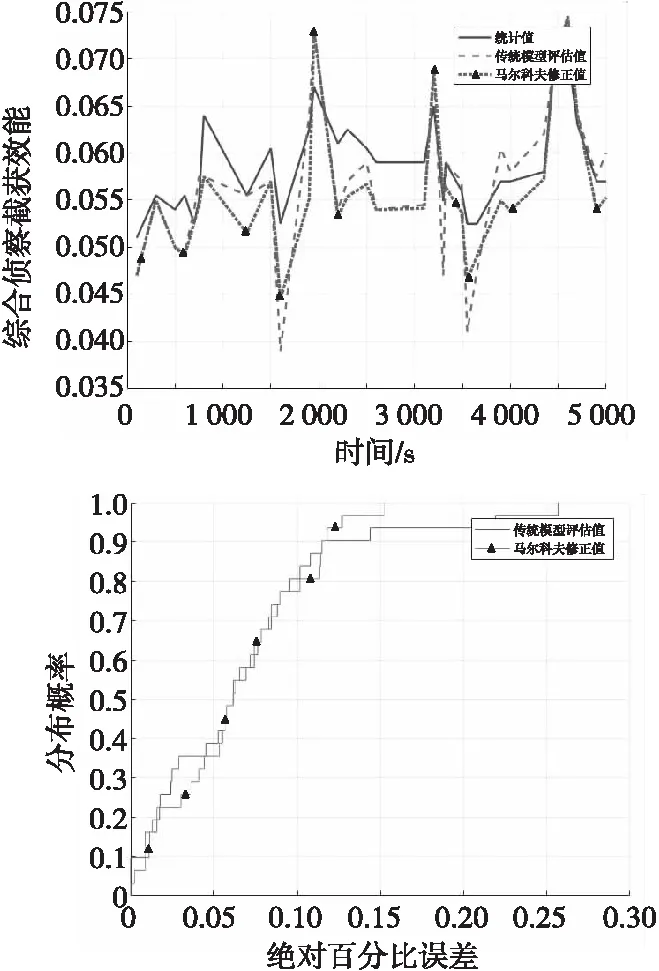
图8 多雷达综合侦察截获效能评估结果Fig.8 Results of comprehensive interception effectiveness evaluation of multi-radar reconnaissance

由仿真结果可知，传统模型评估值90%以上与统计值百分比误差在14.0%以内，平均百分比误差为6.7%，均方误差为0.012 1。马尔科夫修正值90%以上与统计值百分比误差在12.0%以内，平均百分比误差为6.2%，均方误差为0.009 8。本文方法误差较小，评估效果更精确。

4 结论

本文提出了雷达侦察截获效能评估的马尔科夫动态修正方法。该方法在进行数据相关性分析的基础上，构造双链马尔科夫模型将历史实际评估结果因素加入效能评估模型中，得出马尔科夫修正值。在仿真实验中，得到以下结论：1) 仿真场景中，评估值与历史统计值凝聚谱值分别为0.845和0.752，表明两种仿真场景下，两者高度相关和显著相关，满足本文方法应用的前提条件。2) 在对单雷达侦察截获效能、多雷达综合侦察截获效能进行评估时，本文方法与传统评估方法相比精度更高，能较好地评估雷达侦察截获效能。后续还应对以下问题进行研究：1) 评估值与历史统计值相关性较低时，如何优化评估方法。2) 对模型进行误差预测和消除时，如何自动寻优避免引入人为误差。