基于轮廓特征的物体分类识别算法研究

邓秋君

（中山大学南方学院信息工程系，广州510970）

0 引言

图像物体分类识别是当今计算机视觉和模式识别领域中的研究热点。有效的物体分类算法被广泛应用于日常生活、工业应用和军事活动等领域。轮廓是物体的最显著的特征之一，因此利用物体的轮廓特征对物体进行分类具有十分重要的研究意义。本文研究了两种基于轮廓特征的图像分类算法，包括基于转角特征的图像分类算法和基于上下文特征的图像分类算法，并将其应用于对水产品（虾）的分类以及手势的识别中。

基于轮廓特征的物体分类识别研究是机器视觉领域研究的重要课题之一，国内外学者对基于轮廓特征的物体分类识别的方法展开了广泛研究，提出了大量描述轮廓特征的方法。

2002 年，Belongie 等人提出了一种基于形状上下文的描述算子，该算子用于目标物体匹配和分类[1]。上下文算子是用于测量两物体形状之间相似点集的一种对应，其基本思想是通过一个有限子集来获得描述对象形状内部或者外部轮廓上的点；然后进一步求出在对数极坐标系中每个点的形状上下文的直方图特征；文献[14]中最后采用相似度的计算方法来衡量待测物体与模板物体之间的相似度，进而对物体进行分类识别。2007 年，Ling 等人提出了基于内部距离形状上下文（inner distance shape context）的物体分类算法[2]。该算法使用物体形状内部距来衡量物体轮廓点上之间的形状上下文差别，该算法在对动物关节体目标及不闭合轮廓形状物体的分类识别中取得了较好的匹配效果。Shotton 等人于2008 年提出利用聚类来构造轮廓的分段库[3]，将提取出来的目标物体边缘信息进行聚类，通过对多种相同种类的目标物体进行处理后，可以得到描述物体局部特征的轮廓分段库，进而通过物体的局部特征来匹配和分类物体。

目前国内在计算机视觉研究领域中，基于轮廓特征的物体分类识别算法在相关方面的研究取得了一定的进展和成果。

2003 年，Zhang 等人提出了谱描述算子[4]。该算子是在变换域描述轮廓特征，通过频谱变换来解决分类处理过程中遇到的难点。2009 年，Bai 等人提出了一种基于主动轮廓骨架模型的物体轮廓描述的算法[5]。文献[5]首先提取出物体轮廓骨架信息，用相同种类的物体训练得到骨架树；接着描述物体轮廓和骨架之间的对应关系；最后用得到的对应关系对物体进行检测和识别。2014 年Wang 等人提出了一种基于轮廓片段集形状鲁棒性的分类方法[6]。该方法是一种紧凑的形状表示方法，即用轮廓片段来进行描述物体形状。在形状描述的过程中，首先使用离散曲线化方法使得每个物体形状的外轮廓分解为凸的轮廓片段；然后利用上下文特征对每一段轮廓片段进行描述，并且使用局部线性编码的方法把轮廓片段编成形状码；最后利用空间金子塔的方法来对物体进行有效的识别分类。

以上为国内外专家学者提出的一些描述物体轮廓特征的方法，这些描述轮廓特征的方法涉及到轮廓区域的方法、变换域的方法以及轮廓上点之间位置关系的方法，它们都有各自的特点。描述物体形状轮廓时，需要根据物体的形状特征选取合适的轮廓描述符。

在提取完上下文轮廓特征之后的匹配过程中，物体会出现旋转不变性问题。而本文中在提取物体轮廓特征之前，用最佳拟合椭圆的方法把物体的轮廓进行旋转，将轮廓主轴归一到竖直方向，从而解决了旋转不变性问题，最后在分类中得到较好的物体分类。

1 算法实现

1.1 算法描述

要上下文描述的是物体轮廓上每个点之间相对分布的关系。基于上下文物体的分类识别的算法研究可以有效的实现物体形状的匹配。本节主要介绍了基于上下文特征的物体分类识别算法的研究，用直方图来表示上下文的特征；在提取轮廓特征的基础上需要对物体进行匹配识别，采用相似度的计算方法来衡量物体形状之间的相似性，判断两者的相似程度。在形状匹配的过程中首先需要计算形状匹配代价矩阵，利用匈牙利算法对匹配代价矩阵进行处理，找到两物体之间最佳的轮廓匹配点；然后采用薄板样条函数对待测物体进行形状扭曲；最后通过计算两个物体形状上下文距离和弯曲能量来衡量两个物体的相似性。物体上下文特征本身具有一定的旋转不变性，但是在实际生活中，由于受到外界因素的影响，同样物体的轮廓形状可能会因为转换角度或者噪声等影响而发生形变。如果单纯的应用上下文特征来进行识别，准确率会很低。本文采用薄板样条函数（Thin Plate Spline）[7]来模拟两个物体的形状差异，把这个差异描述成一种物体形状到另外一种物体形状的形变，即通过转换把一个形状上的点映射到另外一个形状上去，这有助于后面的识别分类。但是由于使用了TPS，上下文特征使物体轮廓失去了旋转不变性，所以本章提出在进行特征提取之前使用最佳拟合椭圆模型（The Best Fitting Ellipse）[8]的方法对物体的主轴进行竖直归一化处理，这样解决了物体的旋转不变性，提高了物体分类识别率。

该算法应用于手势识别的研究中，选取的数据集为手势图像，采用上下文特征来描述物体轮廓，利用相似度的计算方法来衡量物体的相似性，进而对物体进行分类。基于上下文的物体分类识别算法框架如图1所示，接下来论文将会对算法流程图中每一步进行详细的阐述。

图1 基于上下文的物体分类识别算法框架图

1.2 图像预处理

图像预处理是对图像进行分割，获得二值图。对于背景颜色一致的图像可以采用简单的阈值处理办法。本章处理的数据集是手势图片，我们要得到手势的形状，可以采用肤色检测的方法来处理彩色图像。本章采用的手势形状数据集是摄像机采集到的彩色图片。在图像预处理中，采用肤色检测模型的分割算法[9-10]对彩色图像进行分割。该分割算法是Hsu 提出的一种肤色检测模型[9]，它是基于YCbCr空间椭圆的肤色建模方法，该方法是将YCbCr坐标空间转换到YCb’Cr’坐标空间中，即采用非线性的变换方法将分段色彩变换到另外的色彩空间并用YCb’Cr’来进行表示。在对图像变换后得到Cb’Cr’所在的区域要通过椭圆模型来对肤色的分布进行描述。其中椭圆的公式可以用式（1）-（2）表示：

其中：

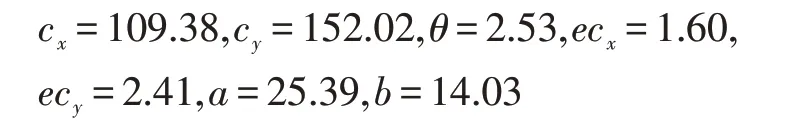
对待测手势图像中的像素经过非线性变换转换到YCb’Cr’空间中，在YCb’Cr’空间中通过检测判断像素的Cb’Cr’值是否在式（2）所描述的椭圆中，如果检测判断的结果在椭圆内，那么就认为此处的像素为肤色点；反之就为背景点。色检测模型的分割算法能够很好地对本节实验图像数据进行分割。

1.3 轮廓提取

图像进行预处理之后需要提取物体的轮廓。假设轮廓点集P={P1,P2,P3,...,PM} ，我们得到的轮廓点集需要能够最大程度的描述物体整体形状，目的是为了让物体形状轮廓边界点质心坐标，和实际物体的质心坐标能最大限度接近。在缩减物体轮廓点的过程中，首先计算物体的质心坐标，假设物体的质心坐标为(x0,y0)，我们通过对轮廓点集P={P1,P2,P3,...,PM} 进行处理，得到如下公式：

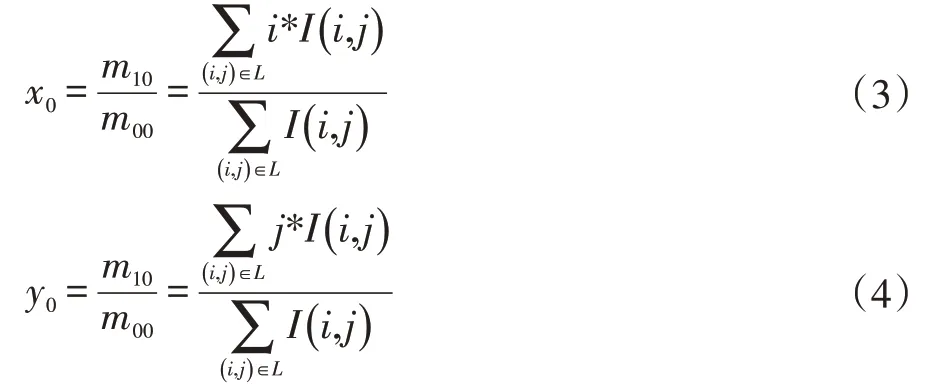
其中L表示物体的形状轮廓，(i,j)是物体轮廓形状的像素点坐标，m10为一阶矩，m00为零阶矩。当坐标(i,j)在形状轮廓区域L中，I(i,j)为1；当(i,j)不在形状轮廓区域L中时，则I(i,j)为0。假设给定的边界点数目为M，选取公式（3）和（4）计算出物体轮廓边界点的质心坐标，并计算该质心坐标与物体实际质心坐标之间的距离，接着不断重复上述过程，最后得到前后两次质心距离最小的M 值。如果M 值越大，说明物体形状轮廓包含的信息就越多，描述物体形状也就越准确，但是会使得计算量变大；如果M 值太小，不能完整地描述物体轮廓信息，并影响匹配效果。因此，选择合适的轮廓点数来描述物体的轮廓至关重要。一般情况，根据经验，在选择上下文特征描述符时，物体的轮廓点数M 的取值在80-160 之间。

1.4 最佳匹配椭圆模型的方法

本文是基于上下文特征的物体分类识别算法的研究。在对物体进行相似度计算时，由于物体在实际生活中，同样的形状会因外界的影响而发生形变。因此在使用上下文特征对物体进行分类识别时，需要使用TPS 对图像轮廓进行弯曲变形以匹配标准摸板物体，提高物体的识别度。但是在使用TPS 后会出现新的问题就是物体会失去旋转不变性，使得相同物体的形状在转换不同的角度后不能很好地进行匹配。因此对于出现的这个问题，本节提出在提取轮廓特征之前采用最佳拟合椭圆模型的方法（The Best Fitting Ellipse）[8]把所有物体轮廓的主轴归一到竖直方向，进而解决最后匹配识别时，采用薄板样条函数（TPS）使得物体轮廓失去旋转不变性的问题。

最佳匹配椭圆模型旋转轮廓：假设对待测物体进行轮廓边缘提取，通过简化轮廓点边缘，得到n 个轮廓点。这n 个轮廓点形成查询对象，使用最佳拟合椭圆模型的方法对查询对象的取向进行标准化，把物体形状轮廓旋转归一到竖直方向。图像f(x,y)的p+q阶几何矩阵定义为：

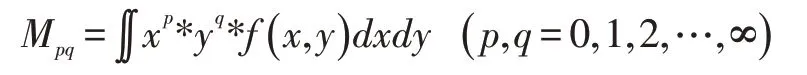
将图像视为灰度值关于空间坐标，零阶矩μ00是图像灰度f(x,y)的总和，二值图像的则表示目标的面积μ00=∬f(x,y)dxdy。一阶矩(μ01,μ10)用于确定图像质心(Xc,YC)：Xc=μ10/μ00;Yc=μ01/μ00;若将坐标原点移至Xc和Yc处，就得到了对于图像位移不变的中心矩。

一阶矩找到幅度分布的质心：

二阶矩描述图像的大小和方向，原始图像完全等价于恒定的辐照度椭圆形，具有确定的尺寸、取向和偏心率，并以图像质心为中心：

图2（a）椭圆的参数中，a 为椭圆的长轴，b 为椭圆的短轴，θ为长轴方位椭圆倾角，θ为主要求的参数。图2（a）为椭圆图，图3（b）为尺度和旋转不变性变换方法举例图。

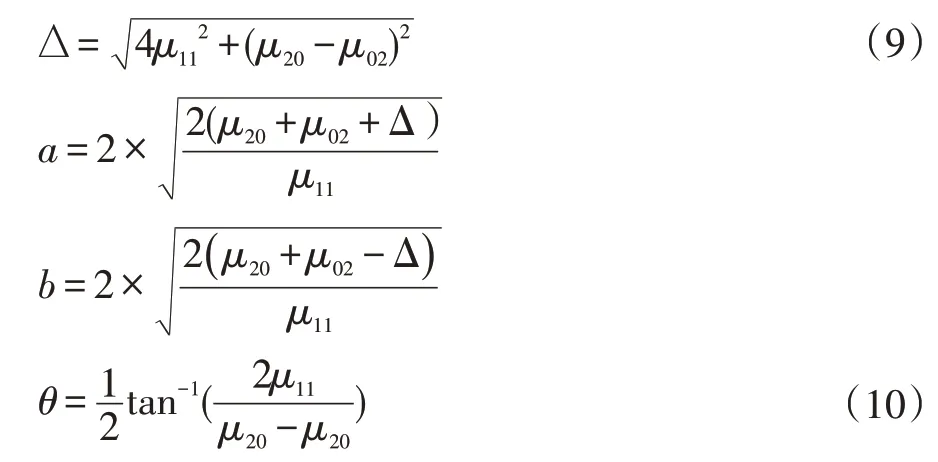
通过式（7）-（9），采用最佳拟合椭圆建模可以得到椭圆的长轴与短轴。

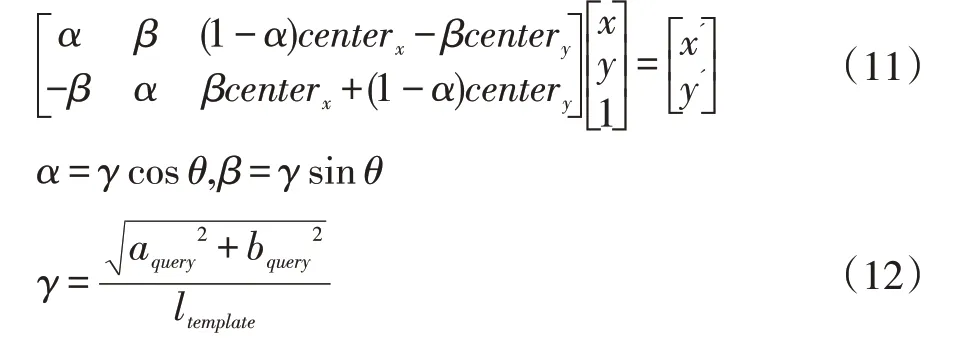
ltemplate是最小矩形模板图像形状的对角线长度。因此查询形状f(x,y)可以通过（10）转化为归一化形状f(x',y' )，而该形状f(x',y' )上轮廓点即为后面待测物体用来描述形状上下文特征的点，图2 为椭圆和尺度、旋转不变性方法示意图。

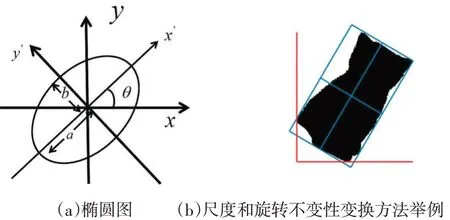
图2 最佳拟合椭圆模型示意图

我们最后会得到旋转变化后的新的轮廓坐标，用于后面进行轮廓特征的提取。如图3 是使用最佳椭圆拟合的方法（BFE）对物体进行旋转的结果。

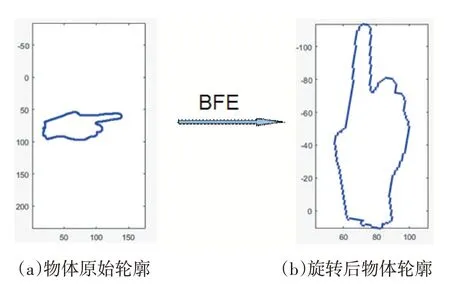
图3 BFE旋转物体轮廓示意图

1.5 形状上下文

1.5.1 对数极坐标建立

采用BFE 的方法对轮廓进行旋转之后，得到新的轮廓坐标。我们把新的轮廓坐标记为：

P={P1,P2,P3,...,Pn} ，对于整个特征点集P，分别以其中的每个特征点P1,P2,P3,...,Pn作参考点，依次计算该点与其余的N-1 个点构成的向量分布直方图，最终得到N个向量分布直方图，并以N*(N-1)大小的矩阵存储。这样，对于任一轮廓目标，可以用N*(N-1)大小的矩阵表示其形状信息，N*(N-1)大小的矩阵即为点集P 的形状上下文，它描述了整个轮廓形状的特征。如图4（c）物体上轮廓点采用极坐标系，将向量的极半径和极角离散化的在空间具体分布描述出来，并且使越临近Pi的点权值越大。

以特征点集中任意一点Pi为参考点，在Pi为圆心、R为半径的局域内按对数距离间隔建立n个同心圆。本方法使用由12 个角度和5 个环组成的对数极坐标系，把空间化分为60 个区域，每个区域的值大小不同。这样原图每个点都可以对应一个维数为60 的向量。轮廓上点的形状上下文这个60 维向量来描述。其计算为（13）：

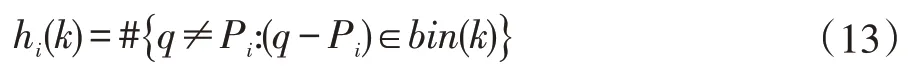
其中k代表极坐标系中的顺序代号，值取0 到60，#表示统计第k个区域轮廓点的个数，q-Pi表示属于点Pi的形状直方图的第k个分量。由于每个轮廓点的对数极坐标空间都有60 个区域，所以点Pi的直方图也就有60 个属性。由公式（a），可以计算出点集P={P1,P2,P3,...,Pn} 的每个点与除它之外的N-1 个点构成的直方图，最后可以得到N个形状直方图。可以用N*60 矩阵表示这个物体的形状信息。矩阵的描述如下：

其中i表示轮廓上的每个点,N 为轮廓上总的点的数目。

图4 B字母上下文轮廓描述

1.5.2 形状直方图

以图5（a）中三角形，长方形和（b）中五角形包围的点为极坐标中心。对于每一个点由r和θ确定的极坐标区域，如果该区域内包含的点越多，则其在由θ和log(r)组成的直角坐标系中，所对应的区域颜色就越深。

利用上下文特征的匹配算法，要求我们对第一个形状上的轮廓点Pi都要在第二个形状上找到一个最优的匹配点。如图5 所示给了字母B，对他们进行匹配，但两者的形状相同。图5（a）和（b）分别对应两个字母的轮廓点集，经过对数极坐标变换可以得到图5 中标注的三个点的形状上下文直方图。即（c）（d）（e）分别为三角形，长方形和正方形所对应轮廓点的上下文直方图。

图5 B字母轮廓点上对应的直方图

从B 字母轮廓上的点对应点可以观察到（d）中正方形轮廓点和（e）中五角星轮廓点对应相似，它们所对应的直方图也相近。

1.6 基于上下文的相似度计算方法

1.6.1 计算匹配代价矩阵

根据上述所描述的方法，可以得到每个物体上下文的形状直方图。要判断第一个物体形状轮廓上的点Pi与第二个物体形状轮廓上的点qj之间的相似度，需要用一个量来衡量，因此可以计算两个物体之间的匹配代价。参考文献[1]计算上下文匹配代价值的方法，对于两个物体轮廓上的采样点间匹配相似度的定量计算，可以进行如下描述：假设有一物体轮廓上采样点集为P，它上面的任意一点为p，另一个物体上的轮廓采样点集为Q 上，它上面任意一点为q。物体轮廓上p,q点处物体形状上下文分别为Hp,Hq。采样点集P,Q为：

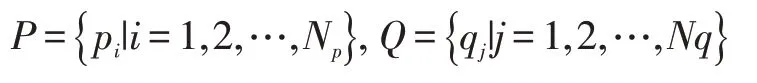
定义点P 与点集Q 之间匹配相似度为字母C，用式（14）定义定义最小匹配相似度：

同样，点Q 与点集P 之间的最小匹配相似度为：

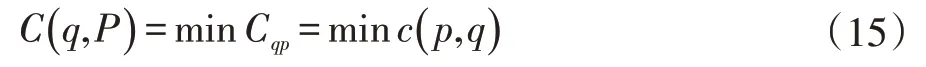
归一化物体形状上下文，使得：

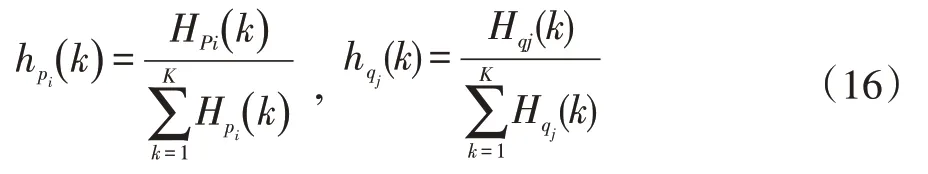
其中，K 用来表示扇形区域块的数量，用统计量表示两个物体之间的相似度：

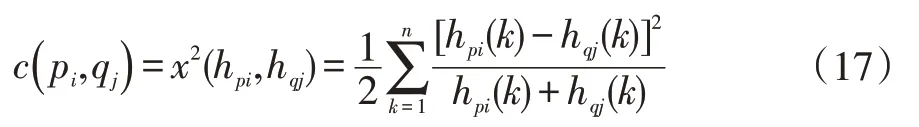
其中hpi(k)表示第一个物体轮廓上点pi的形状上下文直方图，hqj(k)则表示第二个物体轮廓上点qj的形状上下文直方图，c(pi,qj)为定义的轮廓上点的匹配代价，可以利用上下文直方图进行表示，并且服从卡方分布，由上述公式（17）表示。

从（17）式子可以看到，对于两个形状不同的轮廓，选择其中一个物体为参照，计算出参照物体轮廓上点pi和第二个物体形状轮廓上任意点的上下文匹配代价。并且可以知道c(pi,qj)的值越小，说明两个物体联系越紧密，相似度越高。

为了找到第二个物体轮廓上点与参照物体轮廓上pi最优匹配的点，由上述提到的公式（17）可以计算出一个大小为n*n 的两物体形状上下文的匹配代价矩阵C。接下来对两物体进行匹配，形状匹配是为了找到可以充当置换匹配π，让轮廓上点的匹配代价和形状匹配代价能够最小。用公式（18）来对形状匹配代价进行表示：

1.6.2 匈牙利算法

两物体轮廓上点的匹配是一一对应的，并且可以看成是二分图匹配。二分图简单来说是把一幅图中的点分成两组，两组点集间存在对应关系，如图6 所示。二分图的最大匹配问题一般采用匈牙利算法来解决。对于两物体轮廓上形状点集之间对应点的匹配问题，可以看成是二分图匹配问题。把匹配代价值最小的那个点当作是最相似的对应点，通过使用匈牙利算法找到最佳对应点集的匹配。

匈牙利算法是我们所知道的解决线性任务分配问题中的一种典型的方法[11-12]，它是用来解决二分图最大匹配问题的经典算法。匈牙利算法的主要思想是寻找增广路，当找不到增广路的时候，该匹配就是一个最佳匹配。增广路指的是从一个未匹配点出发，经过交替路，如果到达的是另外一个匹配点，则这条交替路为增广路。交替路指在二分图中从未匹配点开始反复经过匹配边和非匹配边的路径。对于一个匹配，如果我们可以找到一条增广路，然后把匹配变成非匹配边，非匹配边变成匹配边，这样就可以多一个匹配。找最大匹配的过程其实是找增广路，当找不到增广路时，该匹配就是一个最大匹配。图6 为二分图示意图。

图6 二分图示意图

图6 是两个字母B 利用匈牙利算法得到的双向匹配图。

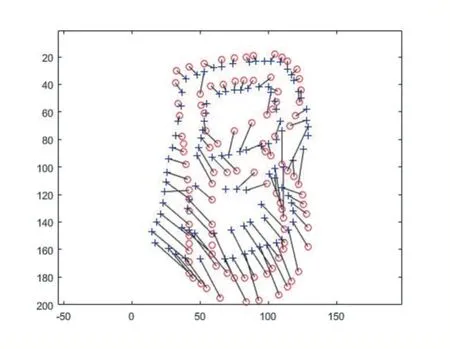
图7 匈牙利算法匹配图

利用匈牙利算法进行匹配时，是基于两物体代价矩阵。如果计算的结果越小则说明两物体相似度越高，反之，则越低。

1.6.3 薄板样条（TPS）变换模型

薄板样条是一种插值方法。以我们常见的一元函数为例，插值是对所给定的点的序列(xi,yi)(i=1,2,…,n)，可以构造函数s(x)使得s(xi=yi),那么薄板样条函数[13]则是在一个二维区域上定义一个三次多项式的插值函数，其实质是自然函数的推广。TPS是通过所有的控制点来形成我们需要的物体的曲面模型[14]，具有很好的抵抗弯曲能力。两个物体形状上的差异可以通过TPS 把它们描述成一种物体形状到另外一种物体形状的形变，TPS 几乎可以近似所有物体的形状。

假设对于已知的点集(xi,yi,zi)i=(1,2,…,n) 可以构造函数表示为s(x,y)使得：

其中(x,y)表示为平面坐标，z表示三维的高度坐标。TPS 的物理意义：假设在二维空间中，有两个物体，对应的点集分别为Q点集和P点集，其表示如（19）。

其中P为原形状，Q为待测形状，Q点集中的N个点用一个TPS 变换来模拟形变，保证这N个点可以正确匹配。

现在需要找到一个函数f使得Q点集映射到P点集，通过f完成两物体轮廓上点的匹配。为了找到合适的f需要定义一个弯曲能量函数，并且使弯曲能量函数最小。薄板样条f最小弯曲能量用式（20）表示。

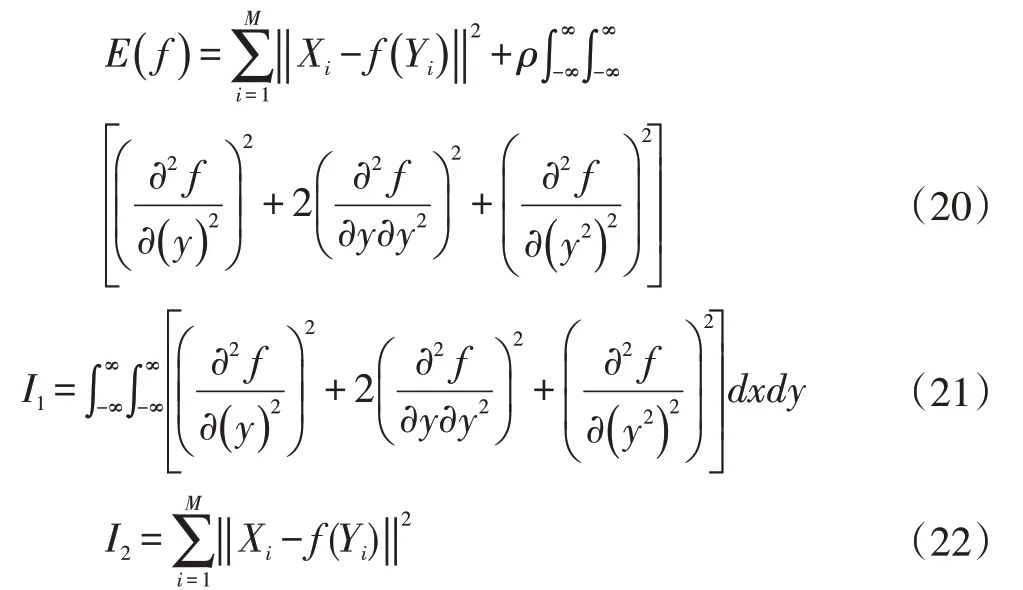
其中Xi表示P点集，Yi表示Q点集；y1表示横坐标，y2表示纵坐标。I2表示点集P与点集Q映射过来点之间的误差或者接近程度，I1表示弯曲函数f的复杂程度，ρ是调节函数f复杂程度的参数使得E(f)最小。当ρ-0 将得到对应的精确匹配。

一般来说，在开始的估算中会包括一些能够减少变换过程中估算的误差，这时需要通过迭代来变换一些点的对应关系和估算转换的过程，通常会选用固定的迭代次数。根据实验经验一般选取3 次为最佳。

1.6.4 形状距离计算

对物体进行分类识别时，需要采用形状匹配算法[15]。物体轮廓上采样点集相似匹配度的定量计算[16]，需要采用Hausdorff 哈夫曼距离Modified Hausdorff Distance（MHD）来作为两轮廓点集之间的匹配测度[17]。MHD 不需要在物体轮廓匹配前进行相应的排序，所以有计算简单的优点，并且两物体轮廓之间的匹配速度较快，具有很好的匹配能力。两物体轮廓点集之间的匹配相似度表示为C(P,Q)-max(Cpq,Cqp),其中Cpq和Cqp表示为对应轮廓点集之间的相似度，用式（23）表示：

在本实验中，采用了上下文的特征描述符，并且在计算相似度的过程中，使用了TPS 对产生形变的物体进行扭曲，使得物体能够进行更好的匹配。实验过程中，通过计算两物体轮廓特征点之间的形状距离和弯曲能量，来衡量物体的相似性，如果计算所得到的数值越小则说明两个物体联系越紧密，相似度就越高。

本文是把两个物体形状上下文距离和弯曲能量加权和作为形状的匹配距离。已知两个物体形状上下文距离，可以用式（24）得到形状映射代价：

该式中T(*)是估计TPS 形状的转换。

如果用If 表示弯曲能量，其中If=E（f），affcost 表示形状映射代价，SCcost 表示形状匹配代价，则最后计算形状距离D=n1*If+n2*affcost+n3*SCcost,通过D的大小来衡量两物体的相似程度，D越小说明两个物体越相似；反之，说明两者相似程度越小。其中n1,n2,n3分别对应弯曲能量，形状映射代价和形状匹配代价的权重，通过改变三者权重的数值得到匹配效果。

2 实验结果与分析

在实际生活应用中，针对生活中驾驶员驾驶汽车接听电话时，会出现因手离方向盘接听电话而造成交通事故的问题，我们可以通过定义手势的形状来控制电话接听功能。在手机中定义几种手势形状来对应电话接听功能，在这个过程中图像只与手势形状轮廓有关。在应用的过程中只需要用手机来对手进行拍照，通过手的形状轮廓来找到对应手机的功能，这样能够避免在行车的过程中，可以不通过手拿手机使用其功能造成不安全隐患的问题。同时也可以应用在人机交互方面，通过电脑摄像头拍照取样处理。主要通过定义几种手型来做二维码，即图形验证码。当网页上出现验证码可以通过定义几种不同的手型来对应相应的验证码。进而能够保障账号的安全，防止暴力破解密码以及广告商注册，发帖和评论。这些可以体现在生活的应用中，所以本章通过选取手型数据集作为实验数据。

本节内容的主要是通过图1 的算法流程完成实验的操作，该实验流程包含了基于上下文特征的物体分类识别算法整个步骤。本实验目的是为了验证本章算法的实效性，看它是否能够解决物体在分类识别过程中因旋转而影响分类效果的问题，并且运用该算法对手势形状进行分类并分析观察它的分类效果。

本文的手型数据集是通过自己用数码相机拍摄采集的，其中相机采用的是索尼（SONY）DSC-RX1002020万有效像素黑卡数码相机，它具有等效28-100mm F1.8-F4.9 蔡司镜头1080P 视频。

本文首先对TPS 算法进行实验演示，对比不同的迭代次数对物体的形状匹配代价，形状映射代价和弯曲能量的影响，因为它们是最后衡量物体相似性的度量。接着进行旋转不变性验证实验，采用的数据集一组是选取5 张手型图片作为匹配模板图，每一张图分别进行12 种不同角度的旋转得到12 张待测图，总共得到60 张待测图，然后用匹配算法来对物体进行分类识别得到匹配结果，通过实验来说明此算法能够解决旋转不变性问题。其次，对实际生活中的图像进行分类识别，选取26 张不同的手势作为匹配样本，用650张包含26 种匹配样本手势形状的待测数据图像进行分类识别，获得识别效果。最后，选用MPEG7 中的5种不同形状的样本图来进行测试，通过实验来说明该算法对形状差异较大的物体识别效果。图8、图9 是部分样本数据集。

图8 五种手型数据集

图9 部分手势数据集

生活中物体的形状会因为外界的各种原因而发生形变。例如，对于手势形状而言，同样一种手型由于手的胖瘦，旋转移动都会使手发生形变，这会影响到物体分类识别的效果。由于TPS 可以有效地模拟待测物体的形变，能够对待测物体进行扭曲以匹配标准模板物体，所以实验中首先展示TPS 的形变模型：

图10 中为选取的两物体手型，实验中对它们进行TPS 模拟形变，（a）是匹配模板物体图，（b）是待测物体图，图11（c）中蓝色和红色标记点的坐标形成的图分别是采样点为100 的模板图和待测图。

图12 为原始两个物体形状没有进行TPS 变换时，物体轮廓的相对位置图。接下来对提取后的物体轮廓用TPS 进行扭曲形变，选取图10 中（a）和图9 中（b）进行分析，根据上文中阐述的方法选点后进行8 次迭代，正规化参数为ρ=1,下面迭代图中用红色圆圈描述的手型是匹配标准图，蓝色圆圈描述的手型是待测图使用TPS 经过不同迭代次数后的扭曲形变图。仿真效果如图13-图17。

图10 物体标准模板和待测图

图11 物体原始图与采样点图

图12 两物体轮廓位置图

图13 第一次迭代

图14 第二次迭代

图15 第三次迭代

从上面的仿真图可以看出，两幅图像在迭代的过程中每次自动调整轮廓点数，并且每次迭代后轮廓匹配相对的点数目发生了细小的变化，这是由于在匹配中通过轮廓上的点循环进行的，每次仿射变换后轮廓上相对应点的位置会发生变化，这使得在下次迭代时候，轮廓上点的匹配位置不同。随着迭代次数的增加，物体形成的匹配代价值在减小。为了验证迭代次数是否对结果产生较大的影响，在上面基础上继续迭代。

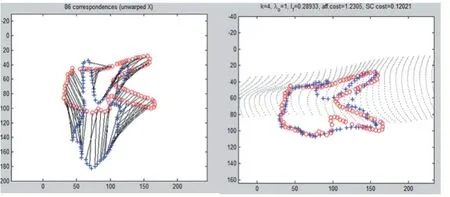
图16 第四次迭代

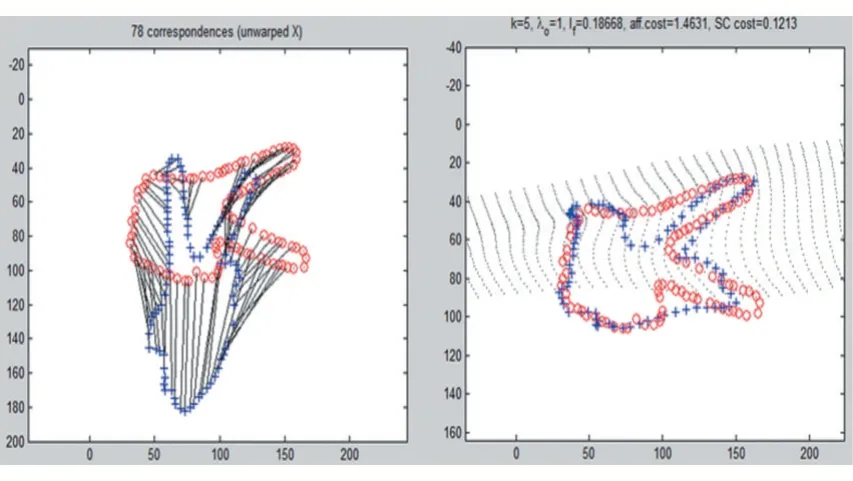
图17 第五次迭代

后面三次迭代就不在一一列举了，在这次TPS 演示试验的过程中总共进行了8 次迭代，得到数据如表1所示。其中If 表示弯曲能量，affcost表示形状映射代价，SCcost表示形状匹配代价。

表1 数据统计

从表1 可以看到随着实验过程中不断增加迭代次数，物体轮廓对应点趋势不断在变化，物体的最小弯曲能量If 不同，但是物体的形状匹配代价在经过第三次之后保持在0.12 左右。

接下来对三组不同的数据，使用该算法来进行实验分类。

（1）旋转变化图片识别

本组实验是为了检测本文算法对旋转变化图像的识别效果。本文选取5 张模板图和5 组数据集进行实验，每组数据集有13 张样本图。实验通过每一组数据集与标准模板的5 张图进行匹配，并得出相应的匹配结果。

其中数据集1 是由图18 中的（a）图通过旋转不同的角度而来，数据集2 是由图18 中的（b）图通过旋转不同的角度而来；同理，数据集3,4,5 分别由图17 中的（c）（d）（e）通过旋转不同的角度而来。

每组数据集有13 张待测物体。

图18 实验匹配模板图

图19 待测数据集1

图20 待测数据集2

图21 待测数据集3

图22 待测数据集4

图23 待测数据集5

实验过程中分别用5 组数据集来与标准模板图进行匹配，最后衡量相似度的距离采用E=3*If+affcost+SCcost。从实验结果来看，每组数据集与标准匹配模板进行匹配得到的匹配率均为100%，匹配度高。说明本文提出的算法能够有效的解决物体旋转性原因引起的匹配识别问题，并且得到很好的分类效果。

（2）手势分类识别

本实验采用26 种不同手型的样本图作为匹配标准，如图24；待测数据为650 张包含26 种手型的测试图，如图25，该图只是待测数据集中的一部分。实验过程中用650 张待测物体手势图与26 种标准模板图进行匹配，实验采用的衡量相似度距离为E=n1*If+n2*affcost+n3*SCcos。其中当n1 =3,n2 =1,n3=1 最后测得的识别率为87.07%，说明该算法能够对手势样本进行有效的分类，在生活中对手势的分类有一定的可行性。

图24 标准匹配图

图25 待测数据

（3）形状差异较大的物体分类

本实验中选用的是MPEG7 种5 种形状各异的物体作为匹配样本，13 种包含5 种匹配样本形状待测物体图，这13 种待测物体与匹配模板物体相比，不仅位置发生了变化，而且也发生了形变，但是他们的形状是一样的。本实验主要是检验本文算法扩展到形状各异的物体分类识别中，观察其分类效果。

图26 匹配结果图

图26 实验最后的数据，图中我们知道图最左边一竖行的五张图是进行二值化后的匹配模板图。表的第一行是12 种形状各异待测物体二值图，在进行实验的过程中，对第一行12 幅图中的每一幅图分别与表中左侧的5 幅图进行匹配，通过计算相似度距离E=SCcost得出相应的结果。图26 中每一列最小值即为两者的匹配对应，即两物体形状距离越相似，匹配代价就越小；反之，则越大，从实验结果来看，匹配率达到了92%左右，匹配率很高。说明本算法能够对形状各异的物体进行有效的分类识别。

3 结语

本文介绍了基于上下文的物体分类识别算法的内容，阐述了最佳拟合椭圆模型算法。它是在提取完物体的轮廓之后，对其进行旋转把图像的主轴归一到竖直方向，主要是为了解决物体分类过程中因位置的变化而使得分类效果变差的问题；接着提取物体的上下文特征，对其进行匹配代价矩阵的计算，通过匈牙利算法来对两物体轮廓上点的最佳匹配，然后使用TPS 对物体进行模拟形变；最后通物体形状距离来衡量两物体的相似性。在实验结果与分析中首先展示了TPS 的形变模型，主要是为了对比不同的迭代次数对物体的形状匹配代价，形状映射代价和弯曲能量的影响；接着进行了三种类型的实验。一是识别旋转变化的图片，目的是为了说明该算法能够解决旋转不变性问题；二是对手势数据集进行识别实验，说明该算法对生活中手势分类问题有一定的可行性；三是形状差异较大的物体分类实验，匹配率很高，表明本算法能够对形状各异的物体进行有效的分类识别。通过三种实验类型结果分析，可以看出本文提出的算法可以有效地对物体进行分类识别效果。