考虑驾驶员预测特性的带有上匝道的宏观交通流模型
2020-09-01巫威眺
翟 聪,巫威眺
(1.佛山科学技术学院交通与土木建筑学院,广东佛山528000;2.华南理工大学土木与交通学院,广州510640)
0 引 言
随着汽车保有量的增加,交通拥挤和交通安全问题变得日益严峻,为有效改善交通现状,学者们提出众多交通管理与控制策略,如公交优化调度策略[1]和车辆控制策略[2].为深入理解交通拥挤形成的原因,学者们相继提出各类交通流模型,包括以元胞自动机模型、跟驰模型为代表的微观交通流模型[3-7];以连续模型为主的宏观交通流模型[8-10].考虑到微观交通流模型注重车辆个体的描述,当道路车辆数较多,研究因素较为复杂时会导致模型不易求解;宏观交通流模型仅需要求解几个参量构成的偏微分方程或方程组,不受车辆数限制,计算时间较少,且注重道路车流整体影响,结合微观和宏观模型的优点,并对两类模型的缺点进行互补,1998年,日本学者Natagani[11]提出格点流体动力学模型,描述单车道上交通流的演化过程.自此,格点流体动力学模型成为宏观交通流理论分析的热点,诸多研究基于此模型进行改进,以分析不同因素对交通流的影响[12-17].
上述各类改进模型都假设道路是封闭的,即不存在匝道的影响,实际上,高速公路路段存在着很多入口匝道,其余道路上的车辆可以由入口匝道汇入主路,高速公路入口匝道车流对高速公路主路车流存在较大影响.2015年,孙棣华等[18]提出带有入口匝道的格点交通流模型;王涛[19]分析主线双车道上交通拥挤演化模式;在未来车联网环境下,文献[20-21]指出驾驶员能够准确获取道路上车辆的具体信息,对下一时刻道路交通状态进行有效预测.然而,在考虑有匝道影响的格点流体动力学模型下,却鲜有涉及对驾驶员预测性的深入研究.为此,本文构造考虑有匝道效应和驾驶员预测性的新格点流体动力学模型,分析匝道流率和驾驶员预测时长对交通流稳定性的影响.一方面可以对研究高速公路入口匝道处交通拥堵成因进行理论分析;另一方面,也可以对高速公路入口匝道处交通拥堵形成和传播进行再现.
1 模型建立
1998年,学者Natagani[11]给出最初版本的格点流体动力学模型,表达式为
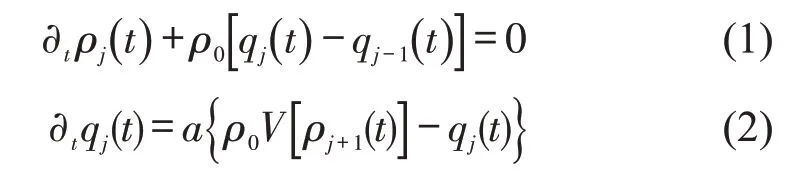
式中:ρj(t)和qj(t)分别为格点j在t时刻的瞬时密度和流量值;ρj-1分别为格点j和后方格点j-1处的瞬时密度;ρ0为平均密度;a为驾驶员灵敏度值;V(·)为最优速度函数,其函数表达式为
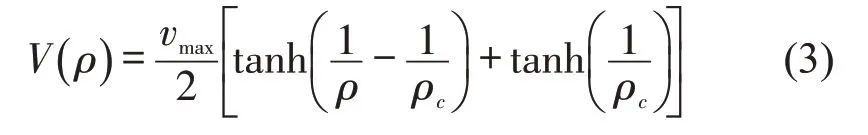
式中:vmax和ρc分别为最大速度和临界安全密度.
式(1)是守恒方程,式(2)是运动方程.
随着交通智能化的发展,驾驶员能够获取更多的周围车辆信息,这些信息有助于驾驶员充分了解当前道路交通状况,作出准确的预测.为研究驾驶员预测性对交通流稳定性的影响,Wang[20]在Natagani[11]模型基础上改进,提出新的格点模型,其中模型的守恒方程保持不变,在运动方程中引入预测项,公式为

式中:τ0为驾驶员的预测时间为前方格点j在未来预测时间t+τ0下的密度与当前时间t下的密度差值;β为权重项.模型中最优速度V(·)不仅与格点j在t时刻的密度相关,还与未来时间段内密度变化有关.
以往研究对驾驶员的预测性进行分析,主要是在单车道、双车道条件下,没有分析匝道上汇入流量对交通流的影响,文献[18,19]论证高速公路匝道流量对主路车流稳定性存在显著影响.为此,本文提出考虑有入口匝道和驾驶员预测性影响的新格点流体动力学模型.新模型的运动方程与式(4)一致,在守恒方程中引入入口匝道流量影响.图1为一类主线上带有匝道汇入的路段示意图.
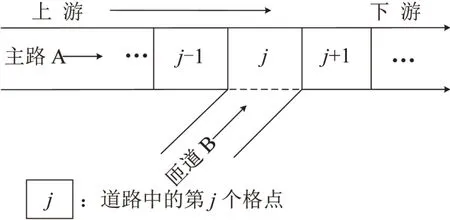
图1 带匝道的交通系统原理图Fig.1 Schematic of on-ramp traffic system
图1中,路段A为主路,路段B为匝道(引道),当匝道B的车流汇入主路A时,使得主路上格点j处的密度要高于后方j-1处的密度,因此,格点j处的交通流入量定义为新模型的守恒方程为
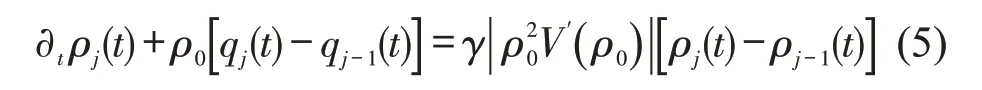
式中:γ为格点j处的匝道流入率为无维量纲变量.
为便于后续分析,对ρj+1(t+τ0)进行泰勒展开,同时忽略高阶非线性项,为此转化为
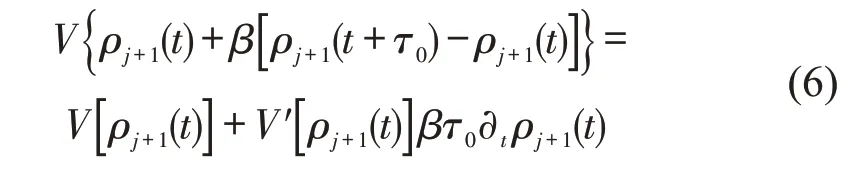
将式(6)带入式(4),可得
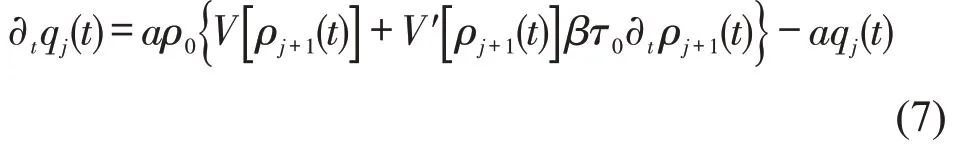
综合式(7)和式(5),消除中间变量qj(t),同时,为便于阅读,在每个表达式中省略时间变量t,得到

2 线性稳定性分析
假设系统处于稳定状态,即初始密度为ρ0,最优速度V(ρ0),可知稳定状态的解为
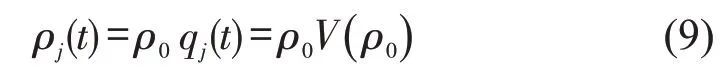
假定yj(t)为稳定状态下的微小扰动,为此,格点j的密度为

将式(10)带入式(8),则变为
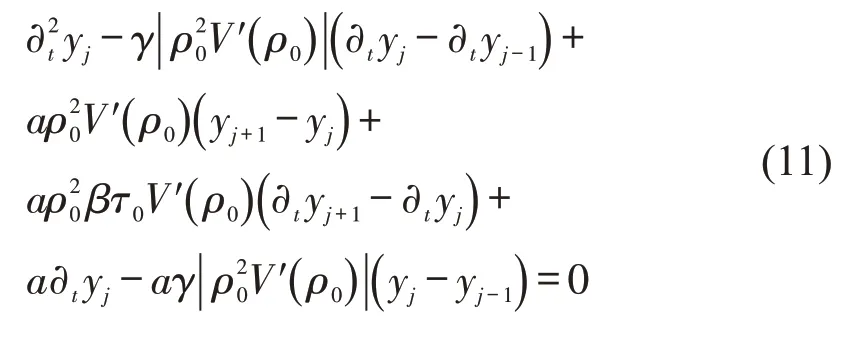
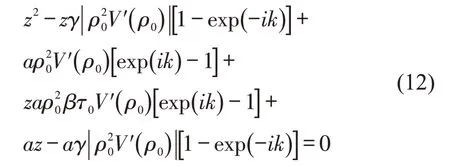
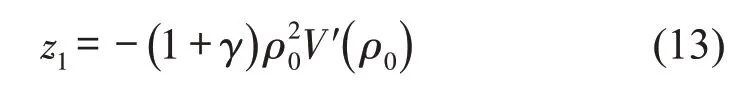
进一步的,将式(13)带入式(12)可得关于(ik)2的二阶项系数为
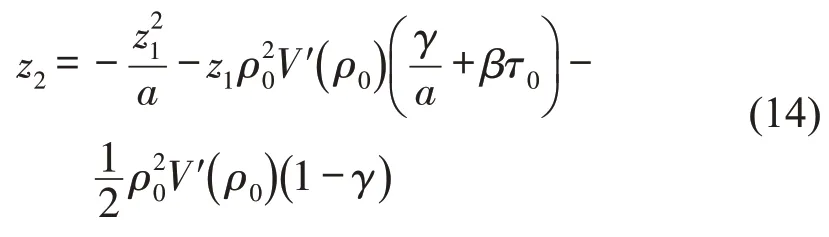
如果z2为负值,则上述均匀交通流变为不稳定交通流,因此,中性稳定条件可以由z2=0 给出,即
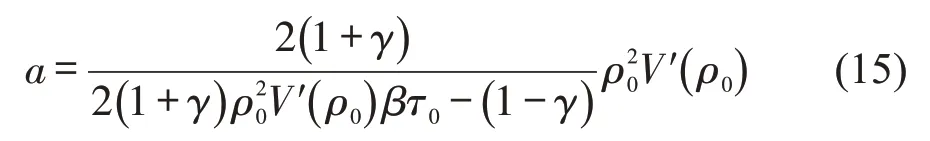
综上所述,得到交通流的稳定性条件为
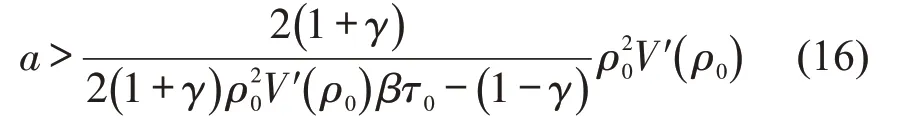
当β=0或τ0=0时,式(16)稳定性条件退化为
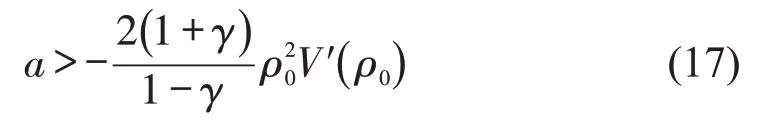
此结论与文献[18]的结论一致.进一步,当γ=0,式(17)与Natagani 格点模型的结论一致,具体为
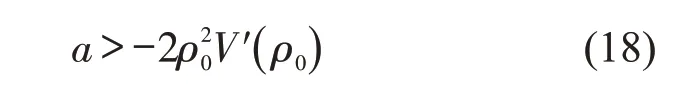
因此,本文的结论可视为上述文献[10,18]结论的一般化形式.
3 非线性稳定性分析
为研究中性稳定曲线附近交通拥堵的演化情形,引入空间变量j和时间变量t,在ε满足0<ε <1下定义慢变量X和T.
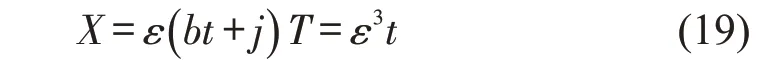
式中:b为待定常数.设密度ρj为

将式(19)和式(20)带入式(8),并展开至ε的5阶项,得到
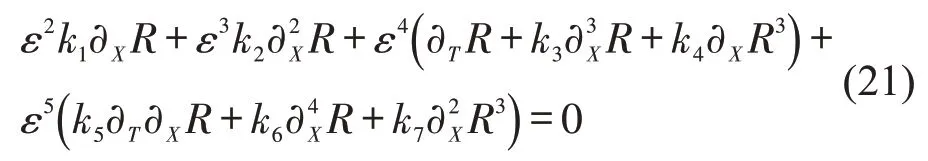
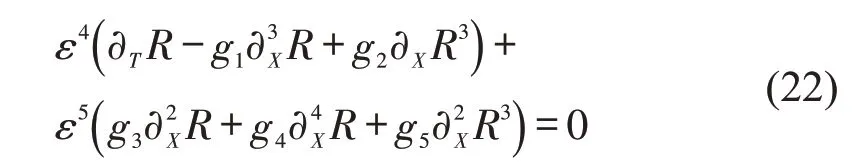
为得到标准的mKdV方程,做变换为
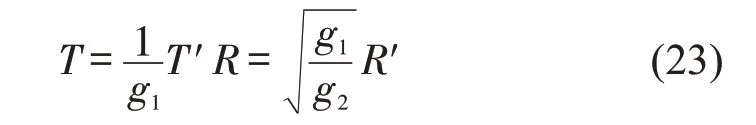
将式(23)带入式(22),可得含有校正项的mKdV方程为
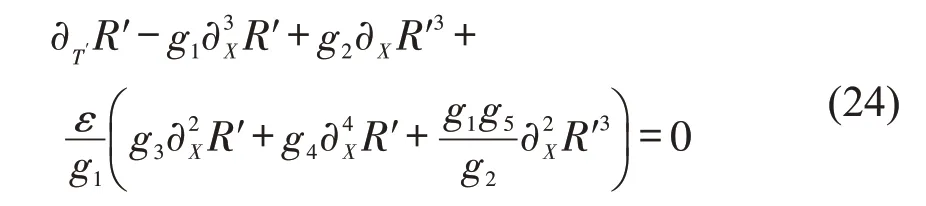
忽略其中校正项,对式(24)mKdV 方程求解,得扭结—反扭结解为
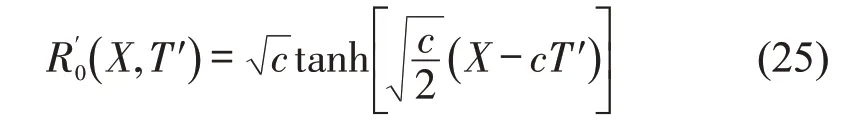
为获取扭结—反扭结解的传播速度,必须满足条件为
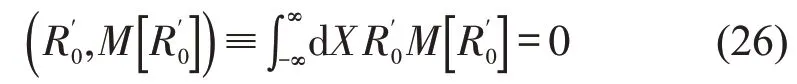
求解式(26),得到关于密度波的传播速度为
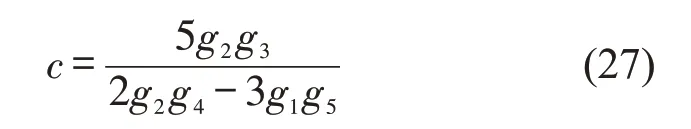
综上,可得扭结—反扭结密度波解为
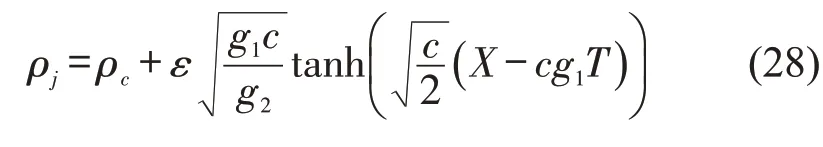
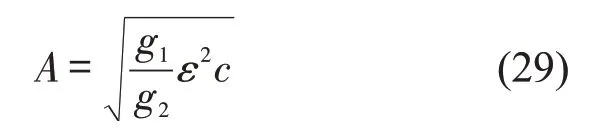
扭结—反扭结密度波解表示共存相,包含低密度区域的自由流运动相和高密度区域的阻塞相,自由流运动相的密度为ρ=ρc-A,阻塞相的密度为ρ=ρc+A.图2为不同参数下密度—灵敏度的相位图,由图2可知:随着参数γ不断增大,即匝道汇入车流流率加快,临界点逐渐上升,表明主线交通流的稳定性区域被压缩,即稳定性变差;相反,随着参数τ0不断增大,驾驶员的预测时间变长,临界点逐渐下降,即主线车流稳定性进一步增强.
为进一步探究参数γ、τ0与临界点ac之间的关系,图3、图4分别从二维、三维角度量化三者之间的关系.由图3可知,参数γ与临界点ac呈现正比例关系;参数τ0与临界点ac表现出完全相反的趋势,图4从三维角度验证上述的结论.
4 仿真算例
为验证上述理论分析的结论,本文在周期性边界条件下,对式(12)进行如下的仿真分析,其中,驾驶员的灵敏度系数a=2,平均密度ρ0=0.25,数值模型的初始条件设置为
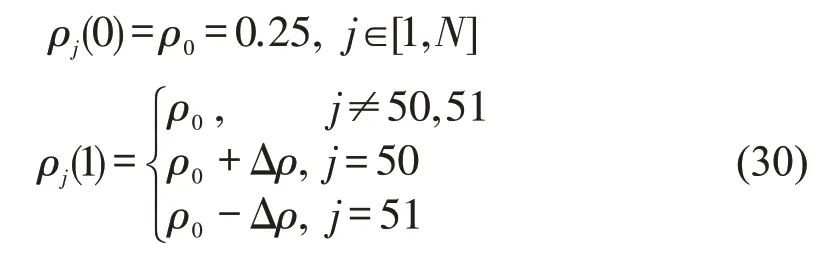
其中,Δρ=0.05,N=100.
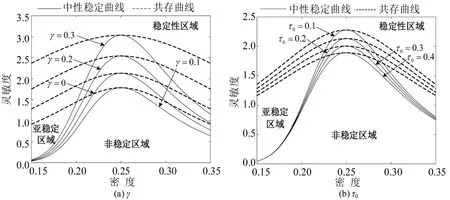
图2 在不同参数下中性稳定曲线和共存曲线的演化情况Fig.2 Evolution of neutral curve and coexist curve under different parameters
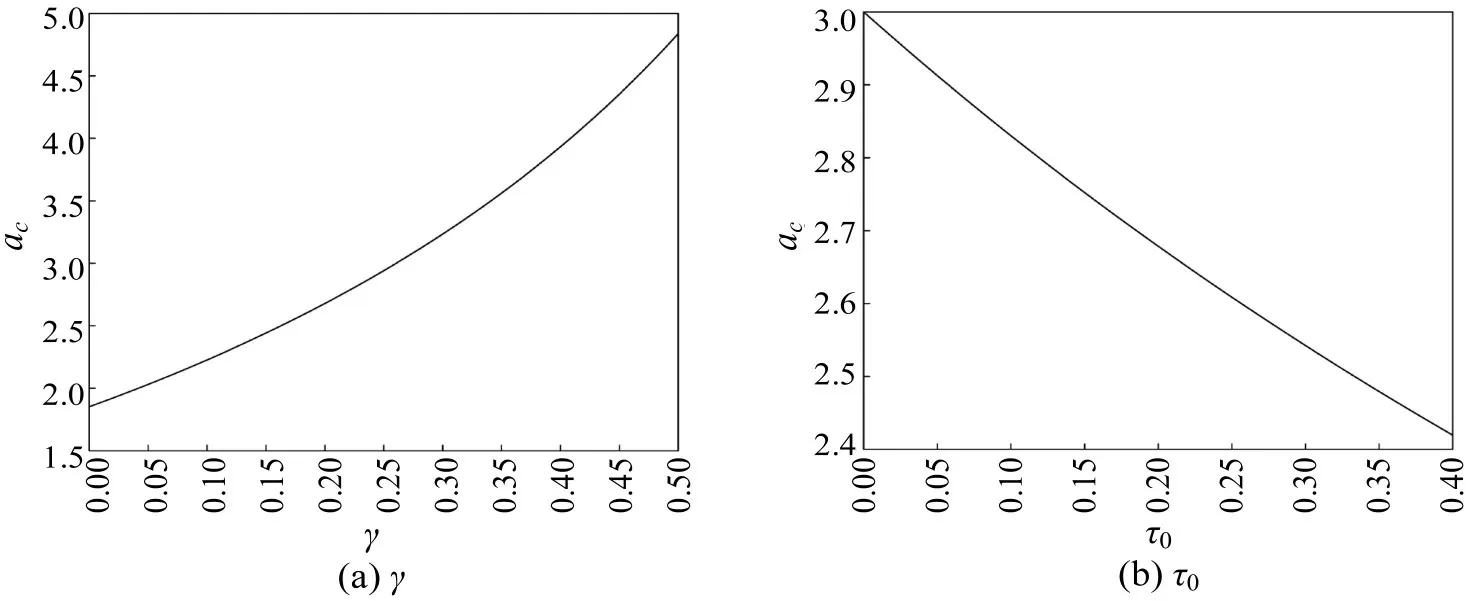
图3 在不同参数下临界灵敏度的取值情况Fig.3 Critical sensitivity against with different parameters
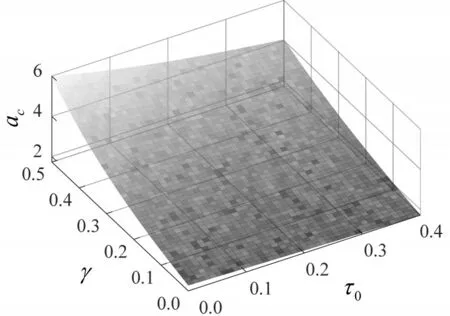
图4 不同参数对(γ,τ0)下临界灵敏度取值情况Fig.4 Sensitivity of critical points under different situations(γ,τ0)
图5为在t=104s后不同参数γ下的密度时空演化图,由图5可知,交通流均演化成阻塞交通流,这是因为稳定性条件(8)未满足,为此初始干扰随时间的演化波动幅度逐渐增大,最终演化成阻塞流.
图6为图5在t=10 300 s时刻下的瞬时密度分布情况.图6中各子图都存在着不同程度的波动幅度,其中,图6(d)的密度波动幅度远高于图6(a),因此,参数γ的增大会一定程度上加剧交通拥堵的出现.
图7为不同参数γ下格点j=50在时间区间t= 60 000~70 000 s 内磁滞回线曲线情况.通过判断磁滞回线曲线所围封闭区域面积的大小判断交通流的稳定性,一般的,所围面积越大,表明交通流稳定性越差.由图7可知,随着参数γ的不断增大,所围面积也逐渐增大.由图5~图7可知,参数γ对交通流的稳定性存在显著影响,且该影响是负向的.
图8为在t=104s后在不同参数τ0下的密度时空演化图.由图8可知,由于稳定性条件(8)未满足,为此图8(a)~(c)中交通流演化成阻塞交通流;当τ0=0.9时,上述稳定性条件(8)得以满足,图8(d)中走停波几乎消失,此时交通流重新恢复到均匀流.
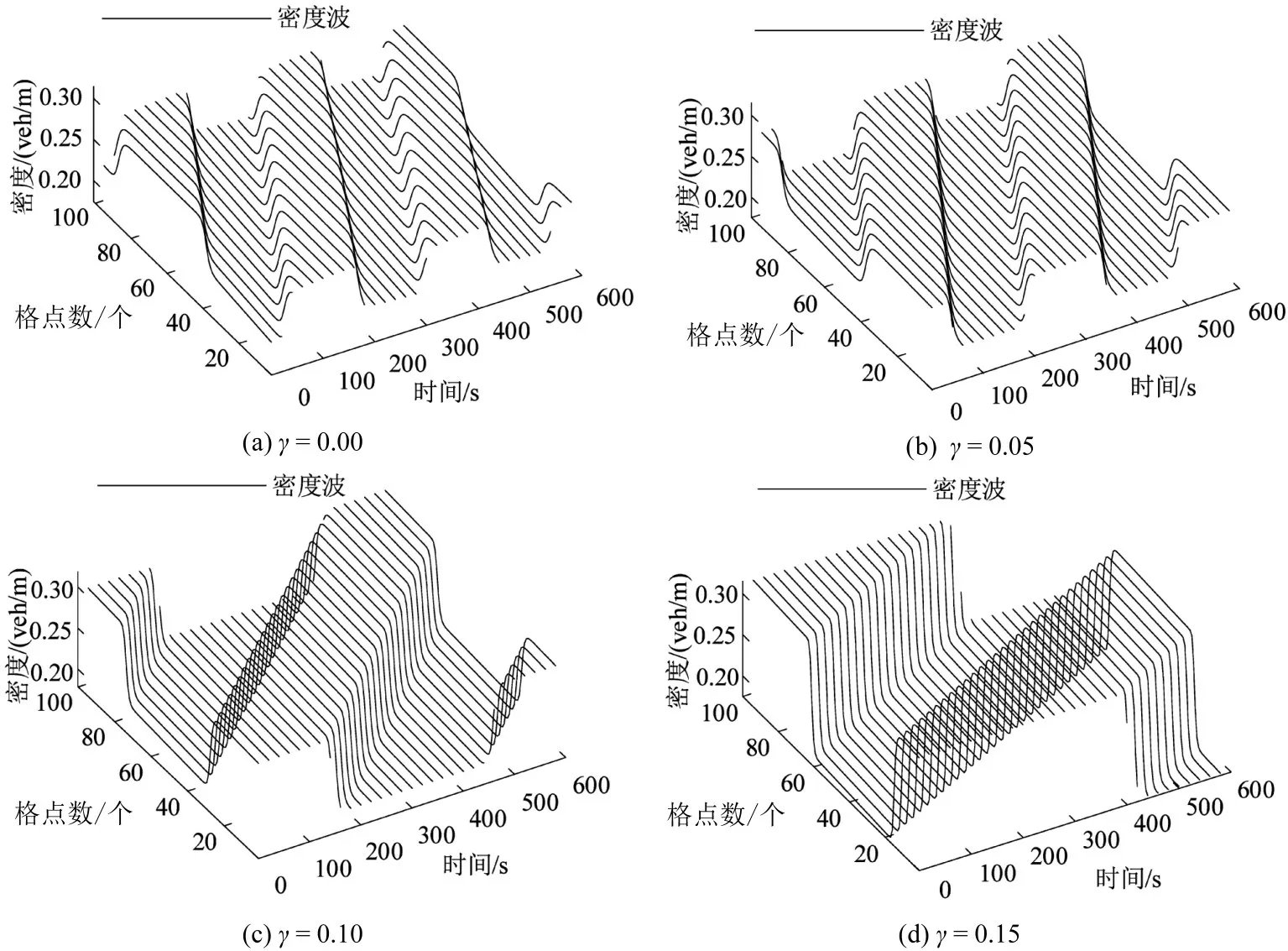
图5 在不同参数γ 下密度波随时间的演化情况Fig.5 Evolution of traffic flow density under different parameter γ
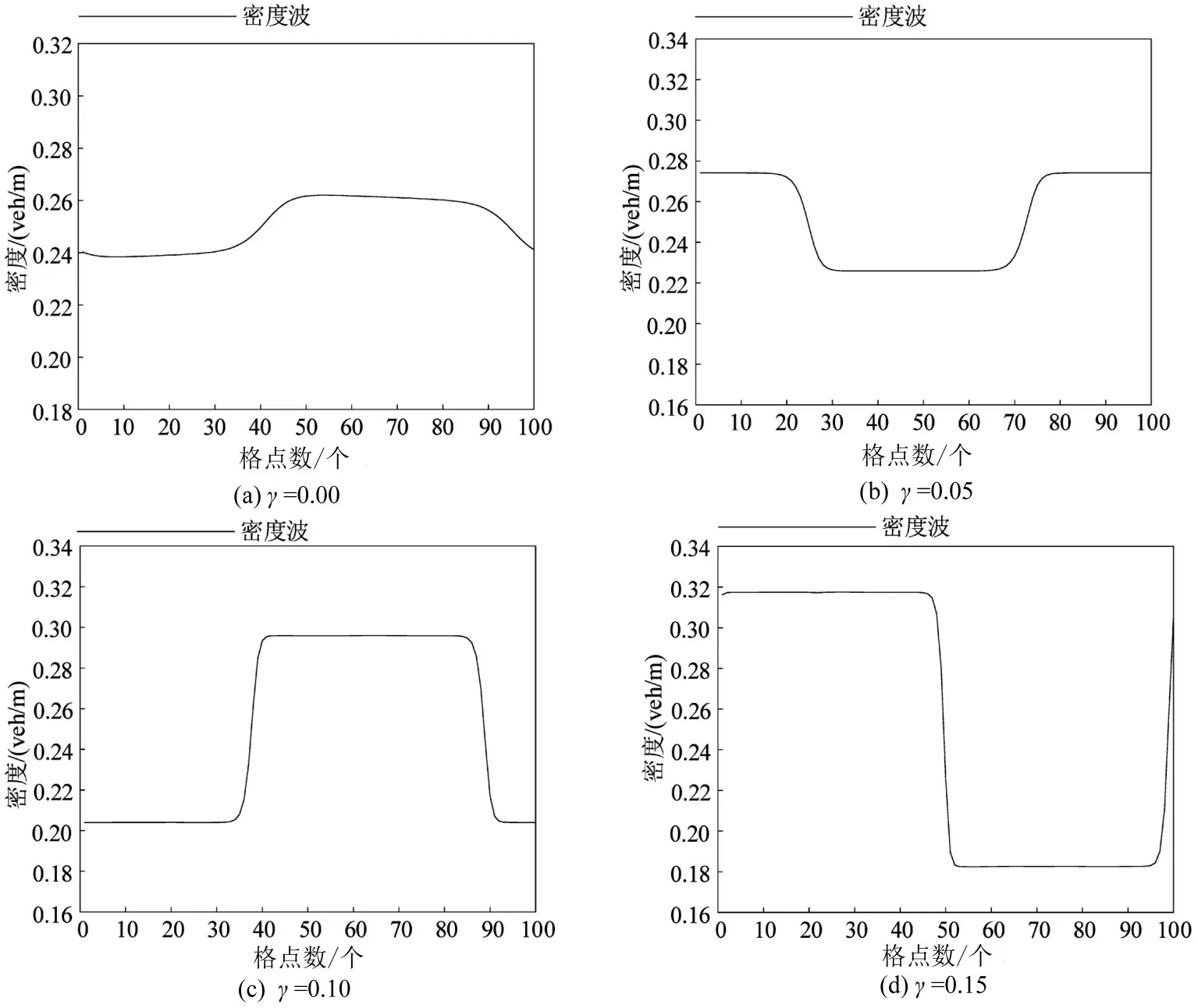
图6 在不同参数γ 下道路上各格点在t= 10 300 s时的瞬时密度分布情况Fig.6 Instantaneous distribution of traffic flow density with different values of parameter γ under t=10 300 s
图9为图8在t=10 300 s时刻下的瞬时密度分布情况.随着参数τ0的不断增大,密度震荡幅度逐渐消失,在图9(d)中密度震荡幅度为0,此时交通流满足稳定.
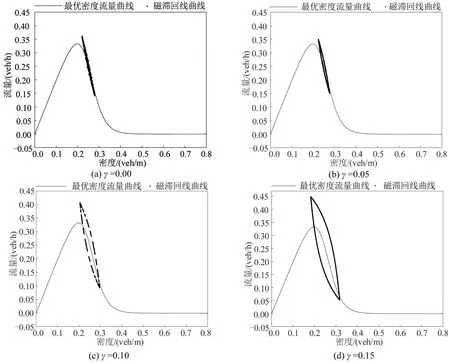
图7 不同参数γ 下新模型的磁滞回线曲线Fig.7 Hysteresis loop curve of new lattice model under different values of parameter γ
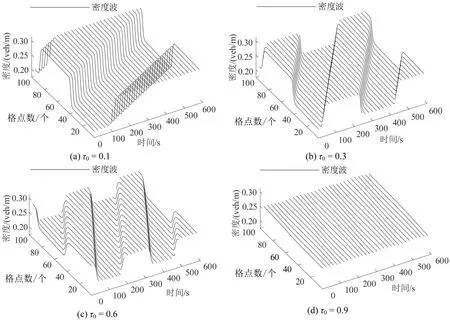
图8 在不同参数τ0 下密度波随时间的演化情况Fig.8 Evolution of traffic flow density under difference parameter
图10为不同参数τ0下格点j=50在时间区间t= 60 000~70 000 s 内磁滞回线曲线情况.随着参数τ0的不断增大,磁滞环逐渐向内回缩,在图10(d)磁滞环收敛于一点,综合图8~图10可得,参数τ0对交通流的稳定性存在显著影响,且该影响是正向的.
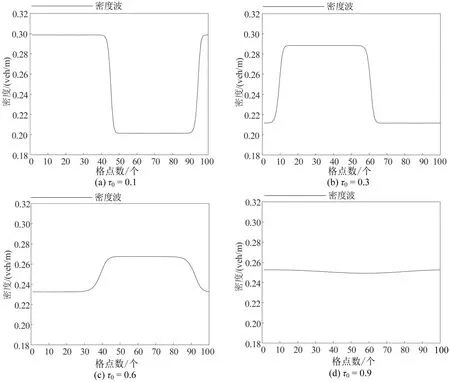
图9 在不同参数τ0 下道路上各格点在t=10 300 s时的瞬时密度分布情况Fig.9 Instantaneous distribution of traffic flow density with difference parameter τ0 under t=10 300 s
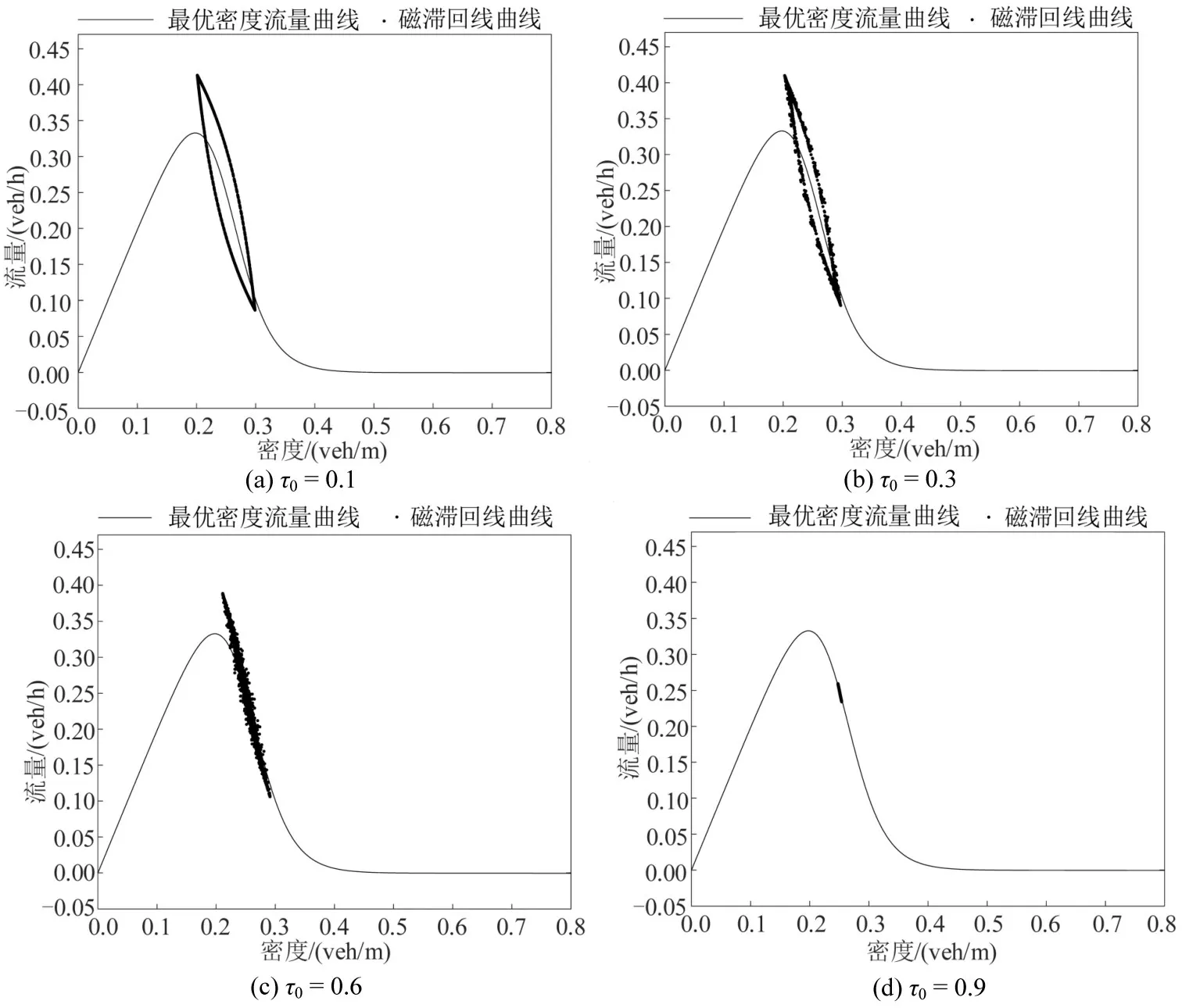
图10 不同参数τ0 下新模型的磁滞回线曲线Fig.10 Hysteresis loop curve of new lattice model under difference parameter τ0
5 结 论
本文通过考虑驾驶员的预测时长和匝道流率对主路交通流的影响,构建新的格点流体动力学模型,基于线性稳定性理论获得新格点模型满足稳定的充分条件,同时基于非线性稳定性分析方法获得关于临界点附近的mKdV 方程,通过求解该方程得到可用于描述交通拥挤演化特性的扭结-反扭结孤立波解,最后以仿真算例验证理论分析的主要结论,即增大匝道流率系数γ会破坏交通流的稳定性,而驾驶员的预测时间τ0与交通流稳定性呈现正比例关系,参数τ0越大,交通流的稳定性越强,交通拥堵越不可能发生.因此,参数γ、τ0对于高速公路主路交通流稳定具有重要影响.
本文研究仍存在一些可拓展之处,例如研究假定所有车辆是同质的,没有分析车辆差异性的影响,因此后续研究可探究异质交通流;另外,研究主要基于仿真算例,缺乏实际数据进行验证,未来将着重对这两点问题进行深入研究.
