基于出行数据的城市公交网络可达性研究

2020-09-01于文涛张可孙会君屈云超

交通运输系统工程与信息 2020年4期

于文涛，张可，李静，孙会君*，屈云超

(1.北京交通大学a.综合交通运输大数据应用技术交通运输行业重点实验室，b.轨道交通控制与安全国家重点实验室，北京100044；2.北京市运输管理技术支持中心，北京100073；3.北京市交通运行监测调度中心(TOCC)，北京100073)

0 引言

可达性是评估交通便利程度的有效指标.生活在具有良好可达性区域的人们，能够获得更多的医疗、教育等机会.城市公共交通具有良好的可达性，同时，能够降低能耗消耗和环境污染，促进城市交通可持续发展.因此，科学评估公交可达性对于城市土地利用、交通网络设计、公交线路调整等具有重要作用.

可达性基础理论发展的比较完善.1959年Hansen[1]将可达性定义为机会相互作用的潜力，可达性研究迅速发展，出现多种可达性的定义及与定义相匹配的模型.交通可达性可以简单理解为：两点之间交通可达的难易程度.经典的可达性模型包括：潜力模型、累计机会模型、效用模型、时空棱镜模型.潜力模型考虑阻抗衰减特性，但是模型中摩擦系数难以确定；累计机会模型考虑阻抗阈值的影响，容易理解并被普遍使用；效用模型主要研究人的出行行为，不易于直观理解；时空棱镜模型用于研究个人出行可达性，需要个人出行数据，对数据要求较高.随着时代发展，研究背景发生变化，通过对上述模型进行变形以适应新的形势，从而使可达性的研究更加深入与细化.

早期公共交通可达性主要基于路网特征、时刻表数据等信息进行评价，之后逐渐向大数据、在线地图方向发展.陈艳艳等[2]利用公交车站、线路等相关指标，结合权重系数评估区域公交可达性.Fayyaz 等[3]采用基于潜力模型的WATT模型评估公交时空可达性.Chen等[4]采用在线地图最短路出行时间评估公共交通可达性，由于在线地图访问次数受限，且非直接数据，研究大城市公共交通可达性时难以获取全面数据.随着POI(Point of Interest,兴趣点)数据的广泛应用，江世雄等[5]构建地铁网络图计算Dijkstra最短路，提出两阶段可达性模型评估地铁可达性，可以提升可达性计算效率.

现有研究一般采用网络最短路径的结果评估公共交通可达性[6]，但最短路反应的是潜在可达性而不是实际可达性，因为实际出行中出行者不一定按照最短路出行，基于实际出行数据评估可达性的研究较少，同时，可达性时间计算中常常忽略线路对等待时间的影响，或者采用调查问卷获取数据并将每个站的等待时间和换乘时间设置为定值[5,7].本文采用换乘时间阈值拼接刷卡数据，直接获取起讫车站出行时间；考虑线路对可达性中出行时间的影响，提出考虑流量和线路的等待时间计算方法，建立两阶段机会模型，以北京市为例，评估公交网络实际可达性.

1 模型构建

1.1 车站服务可达性

通常情况下，公交服务范围内的POI是人们出行的起讫点.将公交车站的服务可达性定义为公交车站服务范围内的机会数，如图1所示，将两点间的欧式距离作为阻抗，服务半径dH范围内的POI计入可达性.

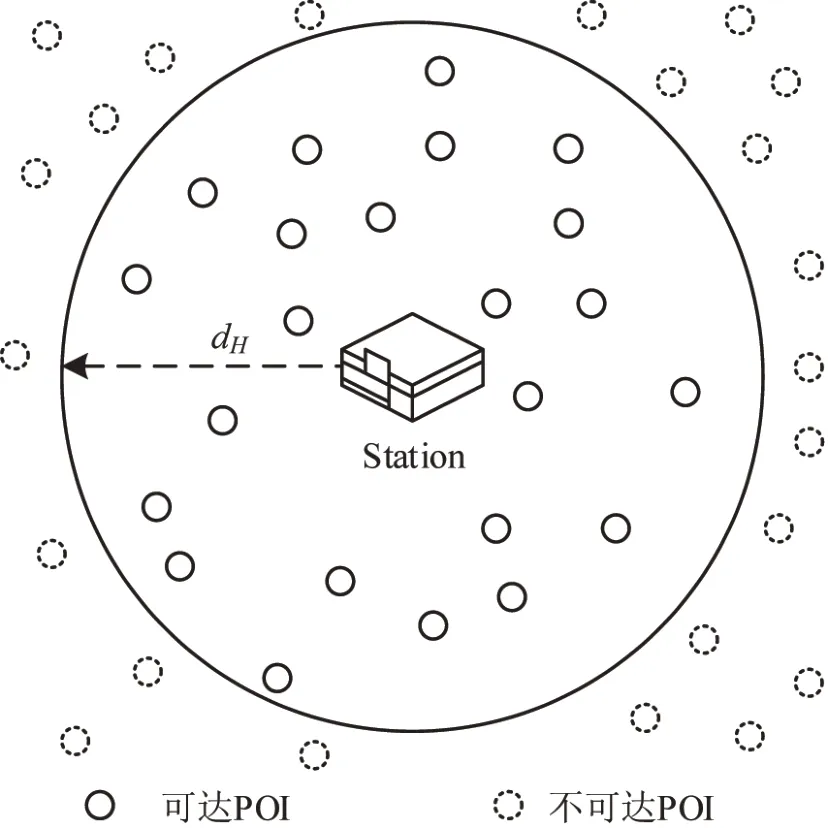
图1 公交车站服务可达性Fig.1 Bus station service accessibility

第1阶段采用机会模型计算车站服务可达性，计算公式为

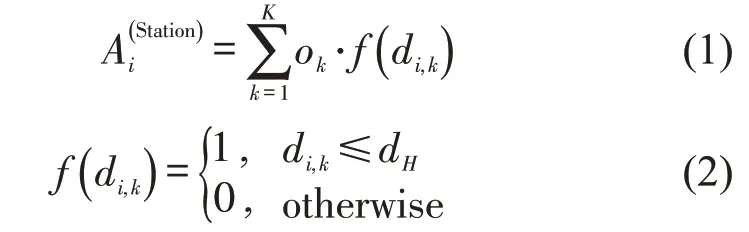
1.2 公交网络可达性

在公交网络可达性评估中，将车站服务可达性作为机会指标，采用车站间平均出行时间作为阻抗，第2阶段为避免摩擦系数的影响，采用机会模型进行网络可达性评估，计算公式为

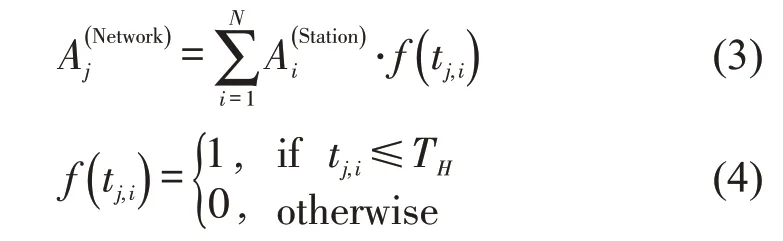
1.3 等待时间

出行时间是可达性评估的关键要素，包括等待、乘车、换乘等时间，考虑车站服务和网络可达性评估中车站线路数目和发车频率对车站等待时间的影响，以及相同起讫车站之间可以通过换乘不同的车站到达，所以无法采用特定车站对之间的等待时间.图2可以得到车站对1至2和1至4的等待时间，但车站对1至5 不能直接求出，因为无法确定出行者是从车站2 还是从车站4 换乘.因此，提出考虑流量和线路的等待时间计算方法，通过等待时间研究线路数目对可达性的影响程度.

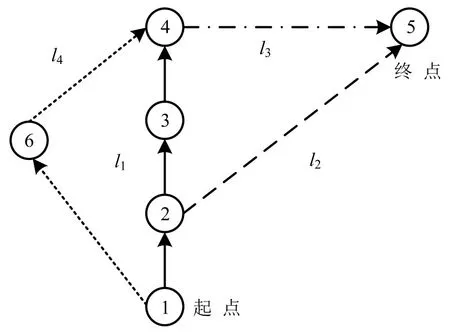
图2 多线路示意图Fig.2 Schematic diagram of multiple bus lines

为便于计算，假设公交发车时间间隔服从均匀分布，计算公式为

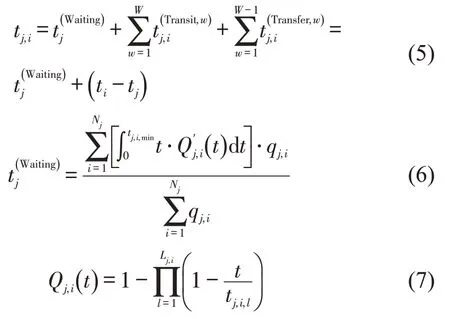
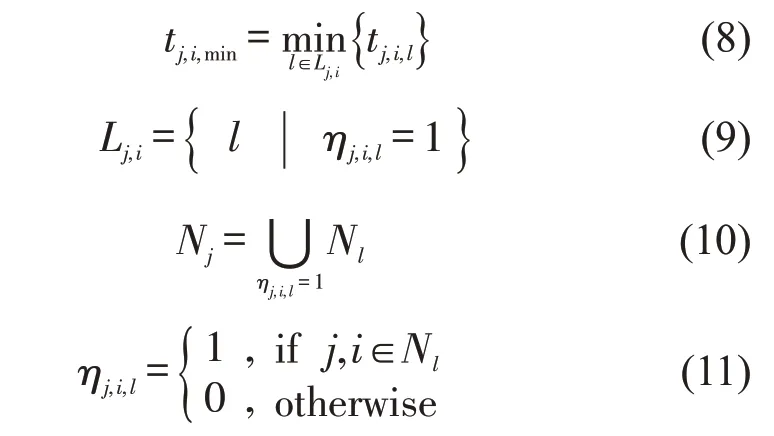
1.4 换乘判定

基于车站的刷卡数据计算起讫车站间的通行时间，需要考虑换乘时间的影响，采用换乘时间阈值的方法，可以剔除时间长的二次活动的数据，降低二次活动的影响，解决将车站换乘时间设置为定值的问题.换乘衔接时间阈值一般不超过30 min[8]，本文将换乘时间阈值设置为30 min，利用该时间阈值判定换乘是否成功，如果成功，认为是一次换乘出行，进行数据拼接，按照起讫车站的时间差计算出行时间的均值；否则，认为是两次出行，保留两次数据.

1.5 等待、换乘时间影响评价

对等待与换乘时间进行差异性设置，研究其对不同等级车站可达性水平的影响程度.影响数量M(levele)和影响比例φ(levele)，计算公式为

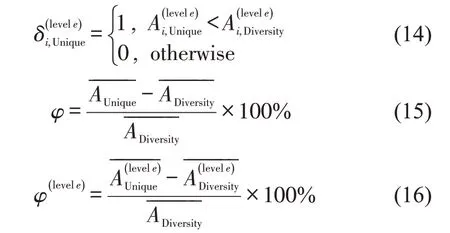
2 数据

采用北京公交2015年8月3∼7日的公交刷卡数据，有效车站3 076个，车站服务范围设为600 m[7].采用投影坐标系EPSG:3 857计算POI与车站间的欧氏距离，选取北京市五环作为研究主体，发车时间间隔数据通过图吧网站(http://bus.mapbar.com)和高德APP 获取，采用高德地图中的POI 数据共计807 308个.数据清洗中删除下车时间早于或等于上车时间的数据及交易不完整数据.

3 结果分析

3.1 车站服务可达性

第1阶段车站服务可达性评估结果如图3所示，结果显示：越靠近城市中心，车站的服务可达性越大，而且沿地铁变化趋势明显.

3.2 公交网络可达性

利用第1阶段的结果进行第2阶段的公交网络可达性评估，将出行时间阈值设定为1 h，如图4所示.结果显示：同公交车站服务可达性具有相似性，越靠近市中心，车站网络服务可达性越大，且沿地铁变化趋势明显.

为分析服务和网络可达性间关系，绘制两者关系散点图，如图5所示.结果显示：两者之间相关性不强；皮尔逊相关系数为0.33，表明两者存在正相关性.进一步分析相关性随出行时间的变化，如图6所示，结果显示：两者之间相关性随出行时间由0.58向0.33递减，表明出行时间越短，两者之间的相关性越大，因为距离越近，车站自身的服务可达性比重越大.

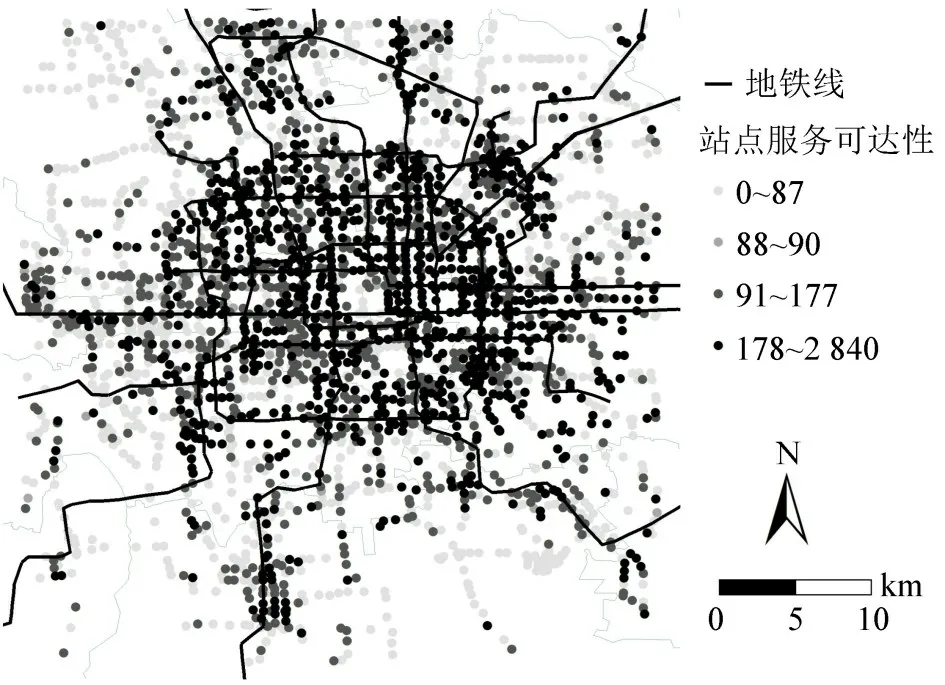
图3 车站服务可达性Fig.3 Station service accessibility

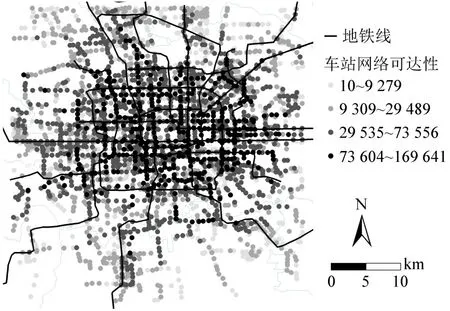
图4 1 h 网络可达性Fig.4 One-hour network accessibility

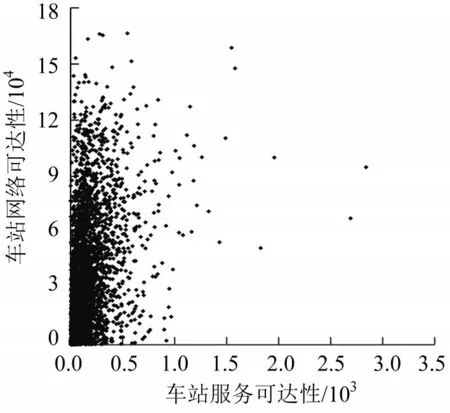
图5 两阶段可达性的相关性Fig.5 Correlation between two-stage accessibility

图6 可达性相关性与出行时间的关系Fig.6 Correlation along with travel time

3.3 等待、换乘时间影响评价

评估等待时间、换乘时间差异性设置对网络可达性的影响，如图7所示，结果显示：出行时间越短，等待时间的影响程度越大；出行时间较短时，高可达性的车站，其线路多、发车频率快，等待时间小于5 min，从而等待时间5 min 定值可达性在短时间内影响较为明显；随出行时间增长，人们能够获得更多的机会，其影响比例逐渐减小.

5 min 换乘时间差异性设置对可达性的影响比例先增大后减小，原因在于10 min 短时间出行时，人们换乘时间多小于5 min，5 min 定值可达性要劣于30 min 阈值可达性，之后随着出行时间的增长，5 min定值设置可达性要优于30 min阈值可达性，在30 min时出现拐点，一方面换乘时间阈值设定为30 min，超过阈值的出行被判定为不可达，另一方面随出行时间增长，人们能得到更多机会，其影响比例逐渐减小.

分析等待时间差异性对不同可达性等级车站的影响.将车站按照网络可达性均匀划分为五个等级，计算1 h内10 min间隔的等待时间随线路变化的差异性设置网络可达性大于等待时间5 min定值设置网络可达性优势车站的数量由表1可知：等待时间定值设置对不同可达性等级车站的影响程度不同.首先，优势车站数目均值为2 034，占总数66.12%；其次，总体趋势上对高可达性区间产生影响的车站数量较多，网络可达性越高的车站，其等待时间相对越短，随网络可达性从高向低变化，优势车站数目均值由612向72递减，可达性越高的车站其等待时间小于5 min的可能性越大.由表2的影响比例可知：等待时间差异性设置对高可达性区间车站影响比例最大，传统的定值设置方法会低估高可达性车站的可达性水平，说明考虑流量和线路的等待时间计算方法具有现实意义.设置网络可达性优势车站的数量由表3可知：优势车站数目均值为1 321，占总数的42.95%；其次，总体趋势上是对高可达性区间产生影响的车站数量较多，网络可达性越高的车站，其换乘时间相对越短；随网络可达性由高向低变化，总体趋势上优势车站数目随之减少，优势车站数目均值由287向198变化.最后，由表4中的影响比例可知：换乘时间定值设置对高可达性区间车站影响比例较大，且出行时间越短，可达性影响比例越大；等待时间差异性设置的影响比例随出行时间的增长而先增加后逐渐减小.

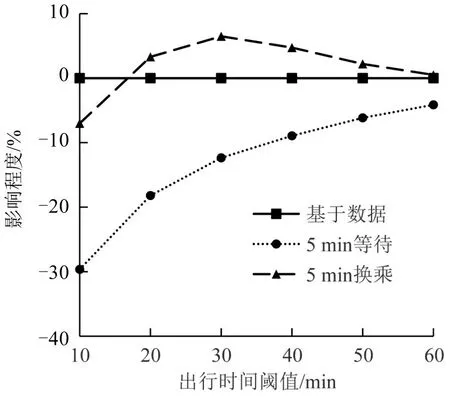
图7 φ 变化趋势Fig.7 Trend of φ

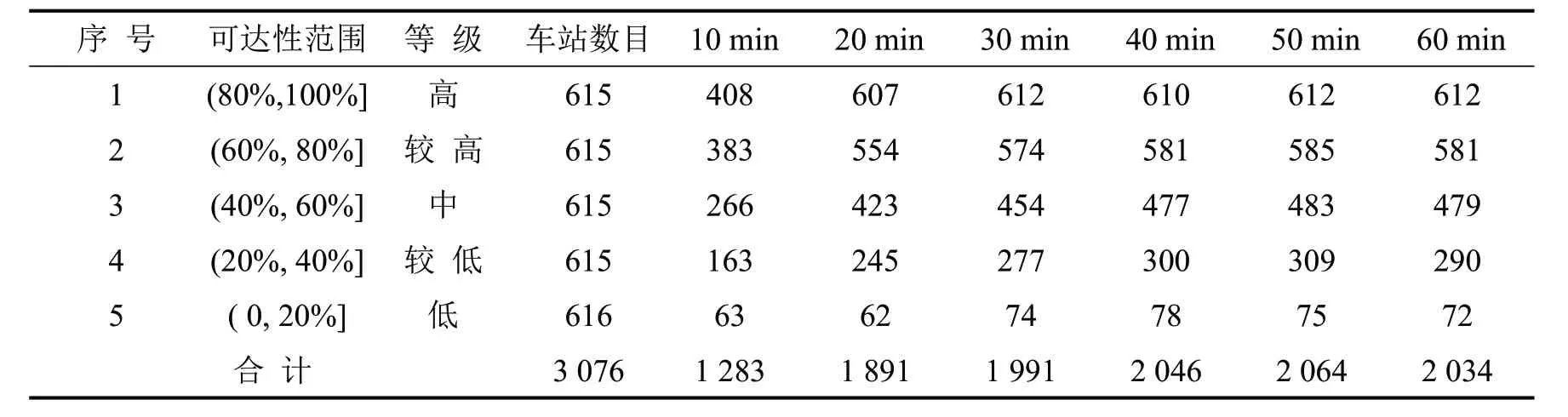
表1 等待时间的影响数量Table1 Number of stations impacted by waiting time

序号12345合计可达性范围(80%,100%](60%,80%](40%,60%](20%,40%](0,20%]等级高较高中较低低车站数目615 615 615 615 616 3 076 10 min 408 383 266 163 63 1 283 20 min 607 554 423 245 62 1 891 30 min 612 574 454 277 74 1 991 40 min 610 581 477 300 78 2 046 50 min 612 585 483 309 75 2 064 60 min 612 581 479 290 72 2 034

表2 等待时间对可达性影响比例Table2 Impact ratio of waiting time on accessibility

序号12345合计可达性范围(80%,100%](60%,80%](40%,60%](20%,40%](0,20%]等级高较高中较低低车站数目615 615 615 615 616 3 076 10 min-61%-50%-27%-10%0-30%20 min-51%-26%-12%-3%1%-18%30 min-35%-18%-7%-2%0-12%40 min-27%-12%-5%-1%0-9%50 min-18%-8%-4%-1%0-6%60 min-12%-6%-3%-1%0-4%

表3 换乘时间的影响数量Table3 Number of stations impacted by transfer time

序号12345合计可达性范围(80%,100%](60%,80%](40%,60%](20%,40%](0,20%]等级高较高中较低低车站数目615 615 615 615 616 3 076 10 min 207 173 110 62 26 578 20 min 240 268 268 230 124 1 130 30 min 156 204 191 208 150 909 40 min 168 189 184 214 162 917 50 min 230 233 222 221 200 1 106 60 min 287 297 264 275 198 1 321

表4 换乘时间对可达性影响比例Table4 Impact ratio of transfer time on accessibility

序号12345合计可达性范围(80%,100%](60%,80%](40%,60%](20%,40%](0,20%]等级高较高中较低低车站数目615 615 615 615 616 3 076 10 min-14%-11%-6%-2%-1%-7%20 min 9%5%1%1%0 3%30 min 15%9%5%3%1%6%40 min 10%6%4%2%1%5%50 min 4%3%2%1%0 2%60 min 1%0 1%1%0 1%

3.4 可达性与线路的关系

根据每个车站通过的线路数目，采用皮尔逊相关系数分析网络可达性与线路数目之间的关系，由图8可知：线路数目与网络可达性之间呈现正相关性，说明线路越多的车站可达性越高；两者之间的相关性随出行时间的增加而逐渐增强.基于数据可达性结果的相关系数与5 min 换乘的相关系数十分接近，而5 min等待在短时间出行时差别较大，说明等待时间定值设置在评估短时间公交网络实际可达性时不合理性最为明显.

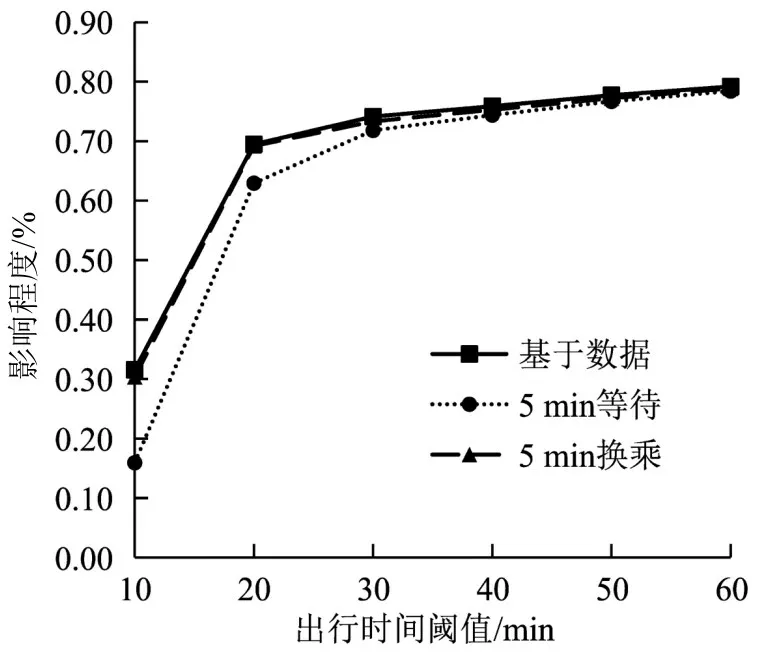
图8 网络可达性与线路数目相关性Fig.8 Correlation between network accessibility and number of lines

分析换乘时间差异性的影响.计算1 h内10 min间隔的根据换乘时间阈值判定基于数据换乘时间差异性设置网络可达性大于换乘时间5 min 定值

4 结论

大城市交通拥堵日益严重，公共交通成为主流出行方式，合理评估公共交通的可达性具有重要意义.本文基于多源数据，提出考虑线路和流量的车站等待时间计算方法，从出行数据中直接提取起讫车站的出行时间，建立两阶段机会模型，从出行数据的角度评估公交网络实际可达性；为避免摩擦系数的影响，第2阶段可达性评估采用机会模型评估公交网络实际可达性，反映线路对可达性中出行时间的影响，有利于识别公交系统实际使用中的薄弱环节，通过网络设计、线路优化提高系统可达性.由于出行时间具有不确定性，公交可靠性的研究是下一步的研究方向.