基于图卷积网络的路网短时交通流预测研究
2020-09-01陈喜群周凌霄
陈喜群,周凌霄,曹 震
(浙江大学建筑工程学院,杭州310058)
0 引 言
随着我国经济发展和城市化进程推进,城市规模逐步扩大,交通拥堵带来的经济损失、环境污染、能源浪费等问题日益加剧,给交通出行者和相关管理部门带来极大不便和困扰.
智能交通系统(Intelligent Transportation Systems,ITS)是缓解交通拥堵问题的有效手段[1].交通流预测是实现交通系统智能化的关键所在,短时交通流预测可以帮助交管部门识别交通流演化态势,提前制定短时交通管制措施,有效缓解交通拥堵,还可以帮助出行者了解路网运行状况,进行路径规划.国内外文献就单个路段或固定检测点位的交通流预测做了广泛研究,但对于大规模路网交通流的预测相对较少,同时,现有模型较少将路网拓扑结构融入预测模型中,因而模型的现实解释意义不强,预测精度有待提高.因此,本文提出基于图卷积网络的交通流预测框架,旨在通过提取交通流时空相关性和路网拓扑结构,实现路网短时交通流预测,实现城市级复杂路网交通流预测,同时考虑路网拓扑结构的影响,提高交通流预测精度.
1 路网短时交通流预测研究现状
国内外有关交通流预测研究大多集中于单点或单一路段上,通常采用ARIMA等参数模型以及机器学习等非参数模型进行预测.例如,Ahmed等[2]首次将ARIMA模型应用于高速公路短期流量预测.Wu等[3]应用支持向量回归(SVR)进行旅行时间预测.由于城市交通环境的复杂性,目前针对城市路网短时交通流预测的相关研究还有待深入.
近年来,学者们将传统模型应用于路网层面,取得较好的效果,Cheng 等[4]提出一种自适应k 近邻(k-NN)模型用于短期路网交通预测;Du等[5]基于传统的交通波模型设计旅行时间预测算法.许多学者借助深度学习强大的非线性数据挖掘能力,提出基于深度学习的路网交通流预测模型,Ma等[6]提出基于卷积神经网络(Convolutional Neural Network,CNN)的方法预测路网交通流量.Yu 等[7]提出基于长短时记忆网络(Long-Short Term Memory,LSTM)的方法,用于高峰期路网交通流预测.根据现有研究经验,混合模型往往比单一模型具有更好的预测效果,Sun 等[8]应用图形拉索(Graphical Lasso)和神经网络融合算法进行路网规模的流量预测;Yu 等[9]融合CNN和LSTM 实现北京路网交通速度预测.
传统深度学习模型虽然具有较高的精度,但未考虑路网拓扑结构带来的影响.图卷积网络(GCN)的兴起为路网交通流预测模型带来新的机遇.Li等[10]提出图卷积循环神经网络(GCRNN)用于预测路网交通速度,并应用于高速公路路网预测;本文提出的模型应用在包含多种道路类型的城市路网,且预测时间间隔更短.Zhang等[11]提出带注意力机制的图卷积网络预测模型,称为AGCSeq2Seq,具有较高的预测精度,混合模型结构相对较复杂,待标定参数数量多;相较而言,本文构建的模型更加简洁,测试路网范围更大.
鉴于ITS和人工智能的快速发展,目前虽已有许多预测算法,每种算法都有其优点和缺点,但由于各种复杂因素的影响,例如路网拓扑结构、交叉口信号控制和交通事故等,大规模城市路网交通流预测仍然是具有挑战性的科学问题.
2 基于GCN的路网短时交通流预测模型
GCN能同时对节点特征信息与图结构信息进行端到端的学习,是对图数据进行处理建模的很好选择[12].本文提出的路网短时交通流预测模型是在基本GCN的基础上进行构建,模型框架如图1所示,在传统图卷积网络基础上形成3个模块:邻接交通流信息提取模块、相关交通流信息提取模块和历史信息提取模块.分别得到矩阵和,通过不同的权重P1、P2和P3加权求和获得最终的输出.
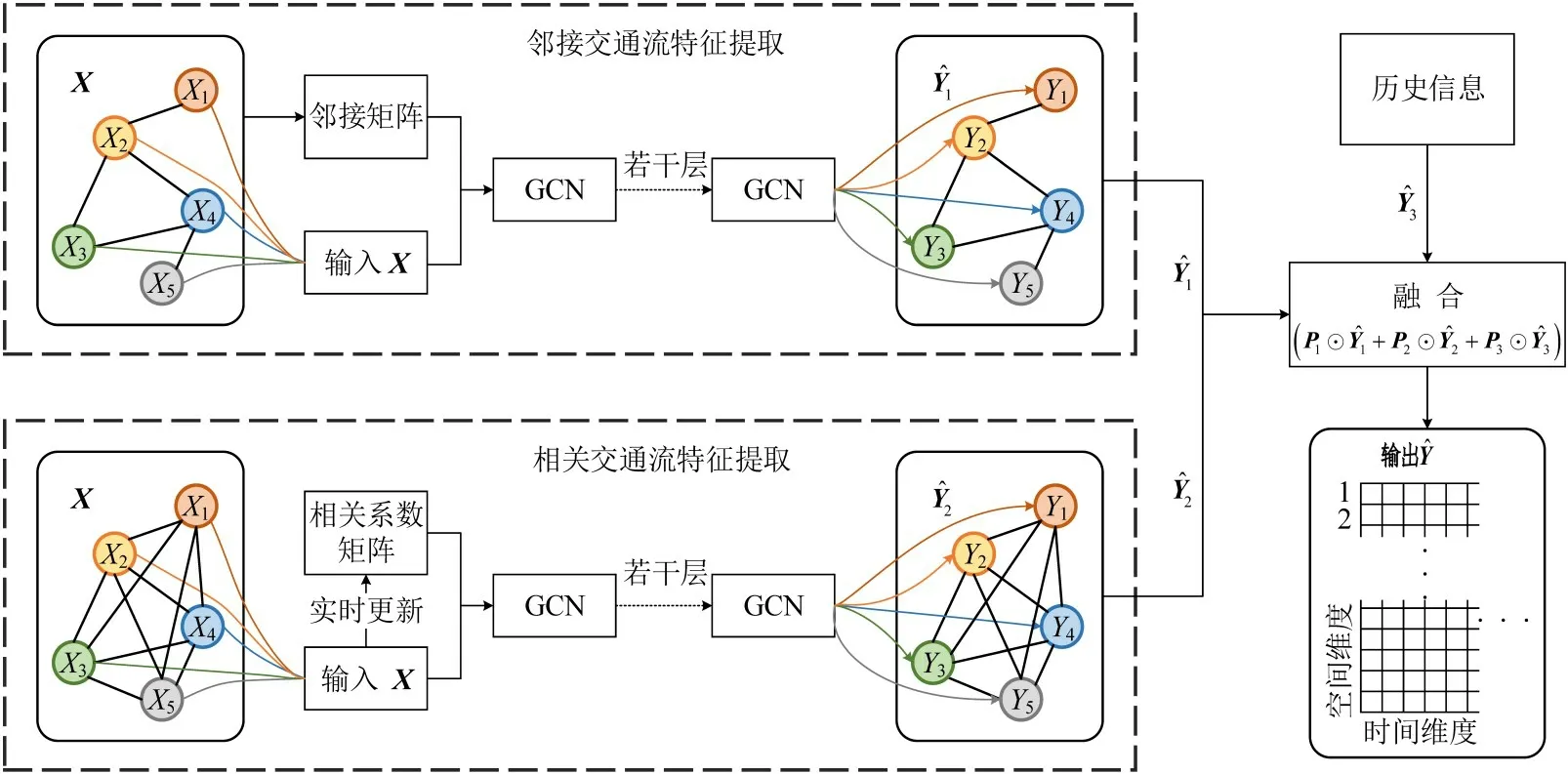
图1 图卷积路网交通流预测模型框架Fig.1 Framework of network-wide traffic prediction model based on GCN
图1所示框架的3个组成模块内容如下:
(1)邻接交通流信息提取(模块I).模块I 考虑路网拓扑结构,输入是由各个路段交通流时间序列堆叠而成的矩阵X.通过各个路段的实际地理位置提取邻接矩阵,若路段在地理上存在上下游链接关系,则认为其邻接.在模块I中,将邻接矩阵A(k)和交通流矩阵X输入图卷积网络进行特征提取,得到最终的输出.其中,A(k)表示k阶邻接矩阵,对于节点i,其k阶邻表示至多经过k个节点即可到达i的所有节点集合.
(2)相关交通流信息提取(模块II).模块II 考虑交通流之间的时间和空间相关性,将图卷积网络中的邻接矩阵A(k)替换为相关矩阵C,其中,C由X通过一系列变换得到,即

式中:f(·)为相应的函数映射,可以是皮尔逊相关系数计算函数,也可以是其他机器学习方法.获取相关系数矩阵C后,和交通流矩阵X输入图卷积网络进行特征提取,得到输出.
(3)历史信息提取(模块III).提取历史上同一时刻的交通流信息,将直接构建成与输出同等尺寸的矩阵.
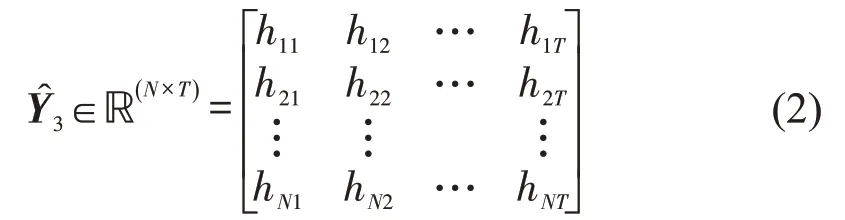
式中:hnt(n=1,2,…,N,t=1,2,…,T)为一定时间之前(如一天、一周、一个月等)路段n在t时刻的历史交通流信息.
(4)矩阵融合.矩阵和通过不同的权重P1、P2和P3加权求和得到输出为
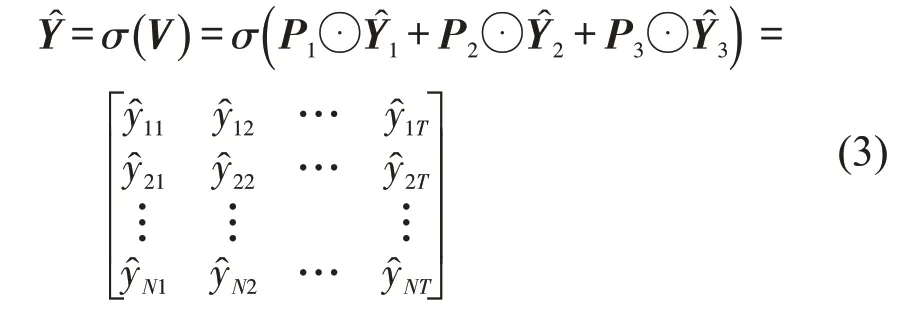
式中:为最终输出;⊙为哈达马(Hadamard)乘子,为矩阵相应位置的数值相乘;表示路段n在t时刻的预测交通流信息.
本文所采用的GCN模型的优势是考虑路网拓扑结构,通过图卷积网络提取出各个节点之间的关系.模型识别出具有关联性的节点,其对应路段在现实中是相邻或存在交通流的相互影响.为可视化这种相关关系,利用节点颜色和大小代表该节点与其余所有节点的相关系数:取绝对值的平均值,即通过提取这些节点之间的相关关系,识别出重要节点对上下游的影响,提高模型的预测精度和可解释性,模块II考虑交通流之间的相关系数矩阵,提取路网交通流之间隐式的相关关系,再结合显式的路网拓扑邻接关系,实现准确的短时交通流预测效果.
3 案例应用与结果分析
为测试构建的图卷积网络交通流预测模型,分析美国马里兰州包含多种道路类型的城市路网,如图2所示,包含高速公路、快速路、主干道和次干道等道路类型,数据来源于区域综合交通信息系统(RITIS).表1为实际路网统计信息,共包含582个路段,单个路段的长度范围为0.010~4.323 km之间.获取的交通流参数是路段平均速度,数据集包含2017年1月1日∼3月31日城市道路网各个路段每5 min的平均速度.
使用前两个月的速度数据作为训练集,剩余的一个月数据用作测试集.使用前60 min 速度数据预测未来30 min的路网速度.激活函数采用ReLU函数,即:Re LU(x)=max{0,x}.
图2 实际测试路网示意图Fig.2 Illustration of test road network
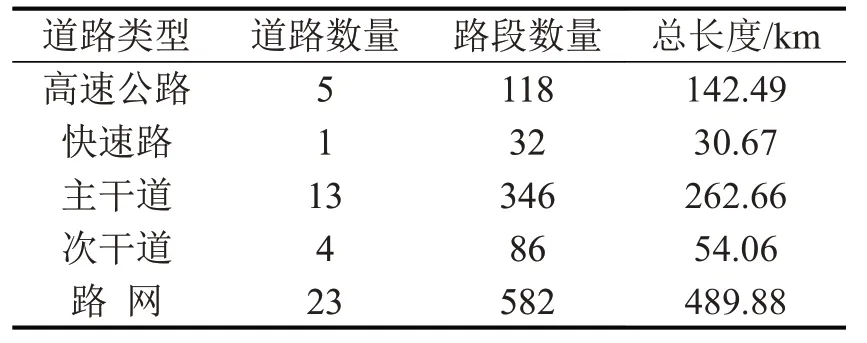
表1 路网基础信息描述Table1 Description for road network
图卷积网络的超参数主要包括:邻接矩阵的k值、隐含层的层数和隐含层神经元个数.在路网案例中,模块II 隐含层数为1层,隐含层神经元个数设定为32,相关矩阵按皮尔逊相关系数计算.
模型共训练80 epoch,采用均方根误差(Root Mean Square Error,RMSE)作为损失函数,计算平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)用以评价模型性能.RMSE和MAPE的定义为
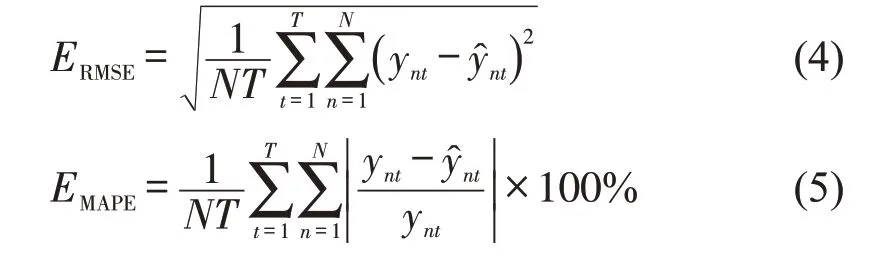
式中:N为路段数量;T为预测的时间间隔;ynt和分别表示速度的真实值和预测值.
图3和图4分别为不同k值和隐含层层数对模型测试误差和效率的影响(仅改变模块I的参数).由图3可知,k值从0 变为1时,预测精度有显著提高,因为,当k=0时,图卷积网络退化为全连接网络,仅考虑交通流相关性,未考虑路网拓扑结构;当k值逐渐增大时,模型精度有所提升,因为较大的k值能使模型捕获更多相邻路段之间的空间相关性;随着k值继续增大,模型的性能提升效果不明显,因为随着阶数的上升,路段之间距离变大,相互间的影响削弱,更多阶近邻的加入使得模型引入部分不甚相关的数据;在同时考虑模型精度和复杂度的情形下,本文选择k=5.由图4可知,随着隐含层数的增加,RMSE和MAPE先下降后逐渐上升.表明在该案例中,较浅层的图卷积网络结构即可捕获复杂的相关关系,随着深度的增加,模型可能出现过拟合问题.
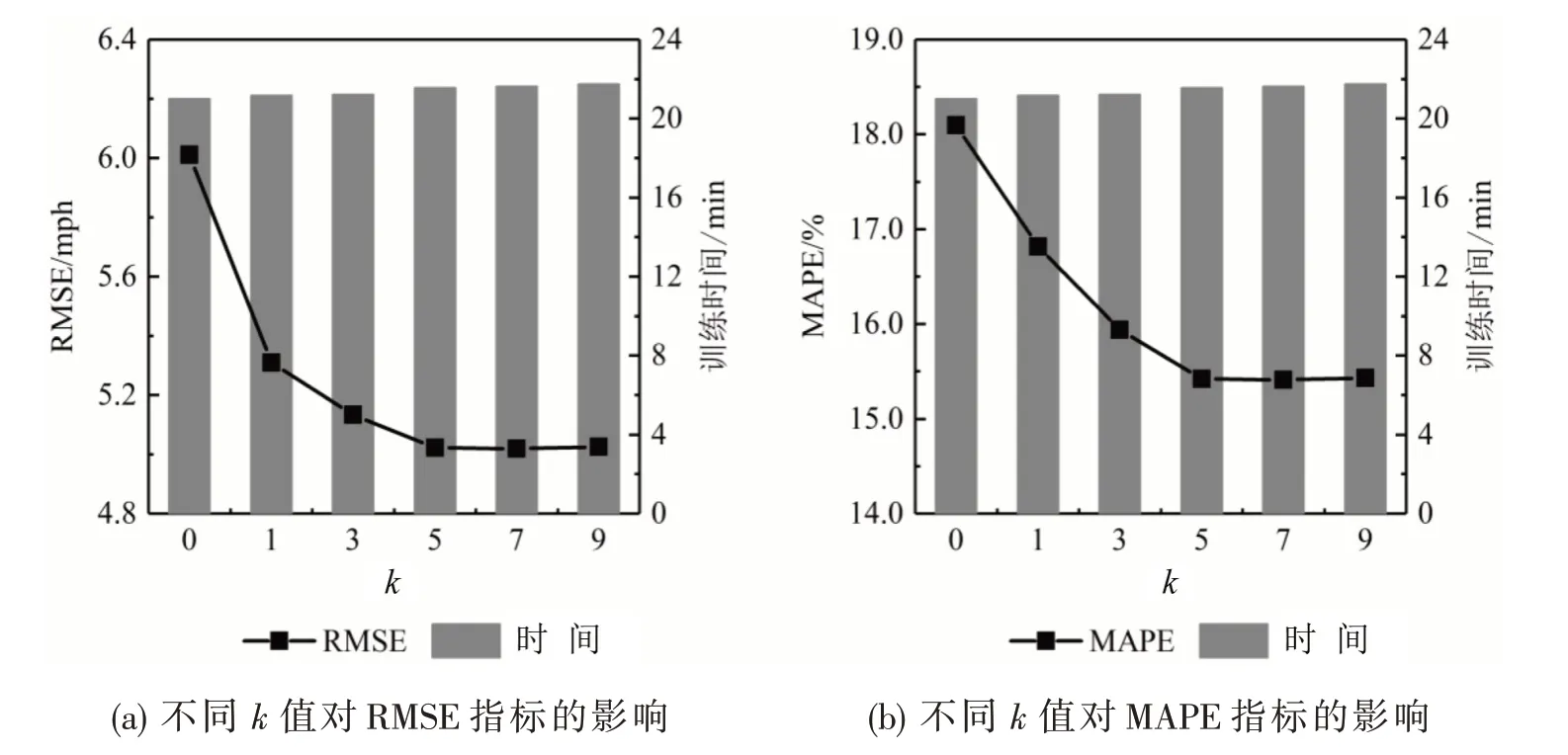
图3 k值对模型性能的影响(1层隐含层)Fig.3 Impacts of k value on model performance(1 layer)
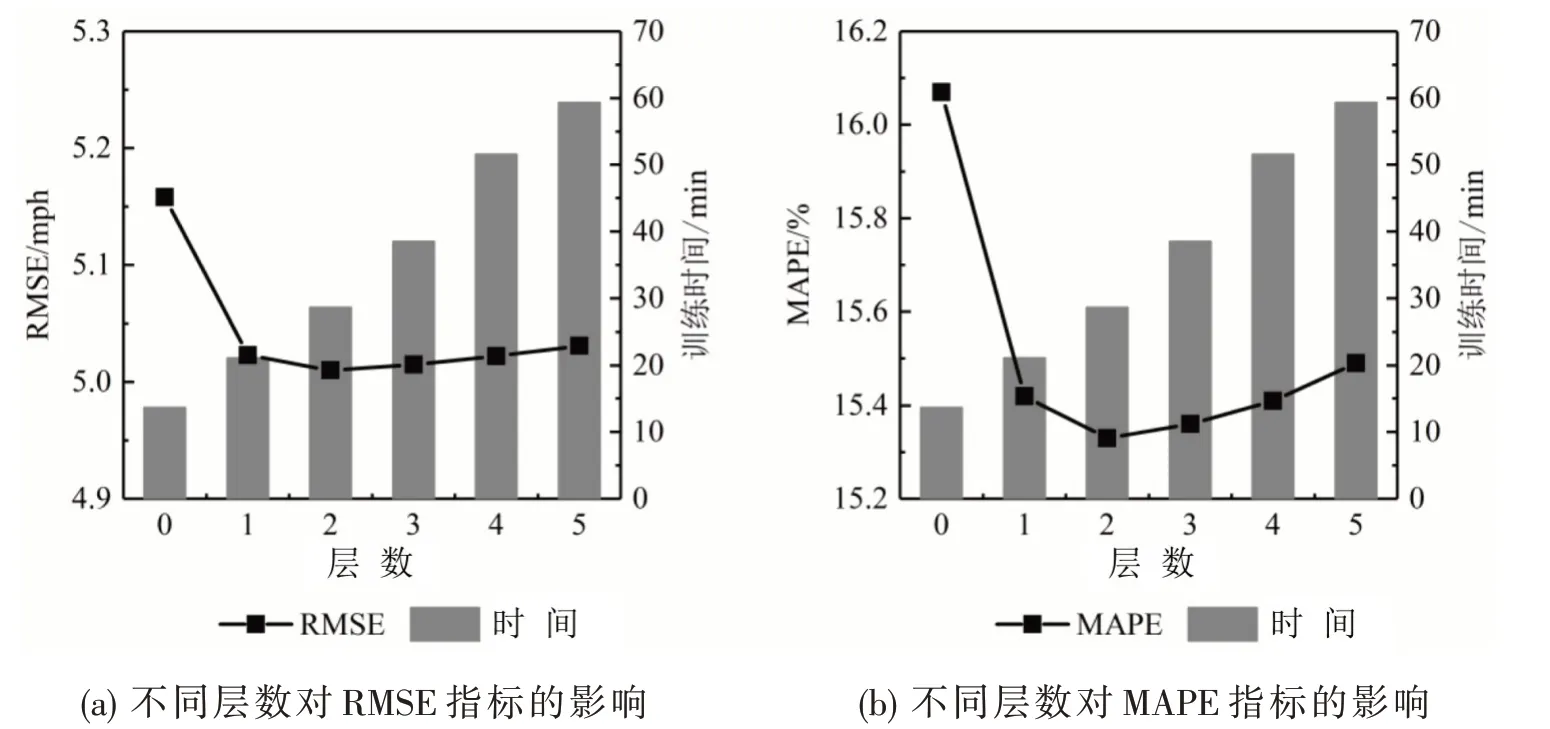
图4 隐含层数对模型性能的影响(k=5)Fig.4 Impacts of number of layers on model performance(k=5)
采用时空深度张量神经网络模型(STDTNN)[13]、历史平均(HA)、自回归移动平均模型(ARMA)、随机森林(RF)、卷积神经网络(CNN)、长短时记忆网络(LSTM)、融合CNN和LSTM(FCL)等现有的模型与GCN模型进行对比,预测性能如表2所示.结果表明,GCN模型在精度指标上均优于基准模型,且在保证精度的条件下,展现出较高的效率.仅考虑相关矩阵的模型也呈现出较好的结果,说明不仅邻近交通流之间存在相关性,一些看似不相关的路段交通流也存在潜在相似性,这通常由路网结构、道路周边区域规划等相似性导致,因此,考虑潜在交通流时空相关性对模型精度也会产生重要影响.同时考虑邻接矩阵和相关矩阵的GCN模型具有更好的效果,表明考虑路网拓扑结构和交通流相关性可以有效地提升模型精度.
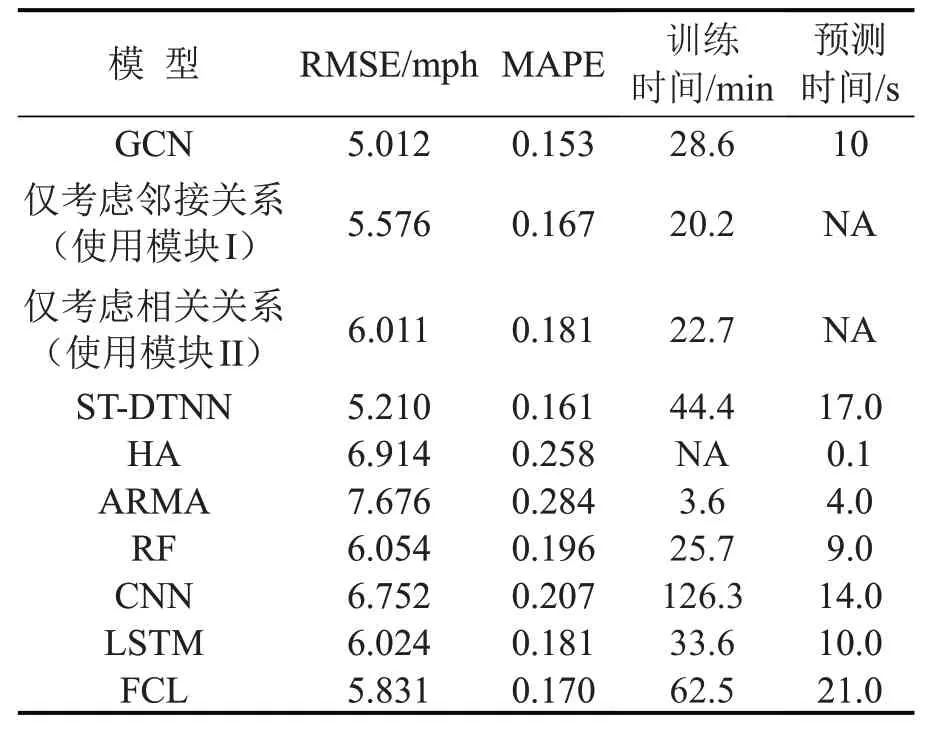
表2 模型预测性能对比Table2 Prediction performance comparison of different models
为测试GCN模型多步预测的效果,同时预测未来30 min(即6步)的路网速度演化规律,表3和表4为不同预测步数下GCN模型的预测误差.结果表明:预测误差随着预测步长的增多而增加,增加量在5‰以内,时间最接近的未来交通速度与当前交通流状况最相关,最容易预测;比较不同道路类型上的多步预测性能,由于主次干道有行人、信号交叉口和分支道路的影响,所以相对更难预测,同时,主次干道的车速较小,其相对误差相应较大.
为进一步测试模型预测效果,提取每天上午07:00-09:00和下午17:00-19:00 早、晚高峰预测结果,将真实速度和预测速度绘制成散点图,45°线表示真实值和预测值相同,越接近45°线精度越高.如图5所示,直方图表示数据在x轴和y轴上的投影,大多数散点接近45°线,且在±10 mph(±16 km/h)范围内,皮尔逊相关系数 PCC(Pearson Correlation Coefficient)为0.857,表明GCN模型在早、晚高峰时期也能保持良好的预测性能.
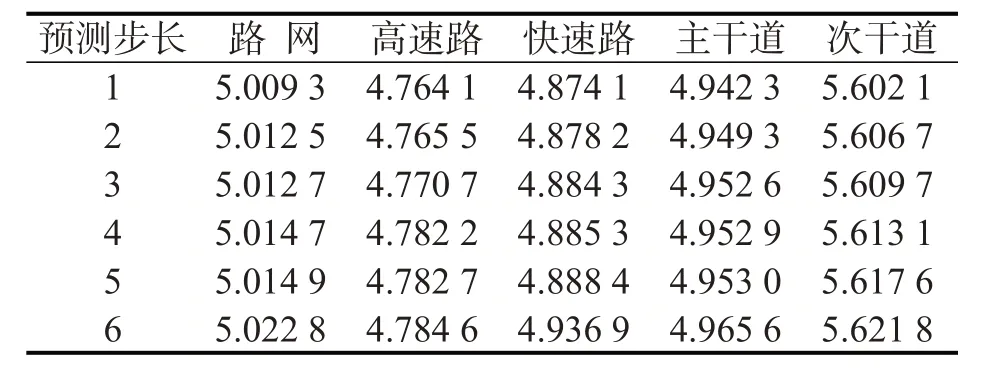
表3 多步预测误差表(RMSE)Table3 Multi-step prediction performance of the GCN model (mph)
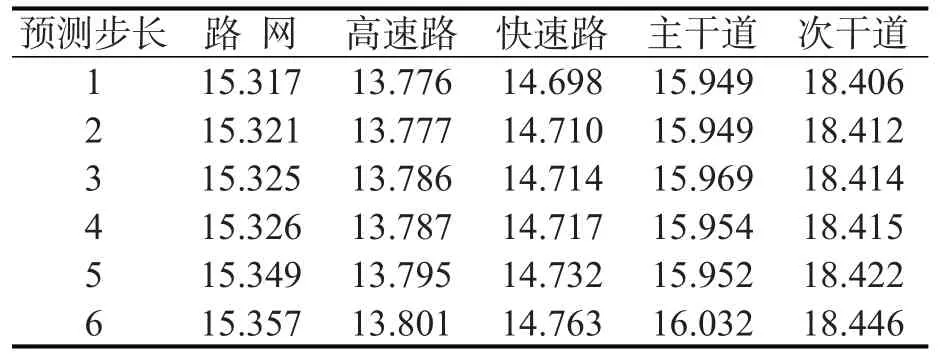
表4 多步预测误差表(MAPE)Table4 Multi-step prediction performance of the GCN model (%)
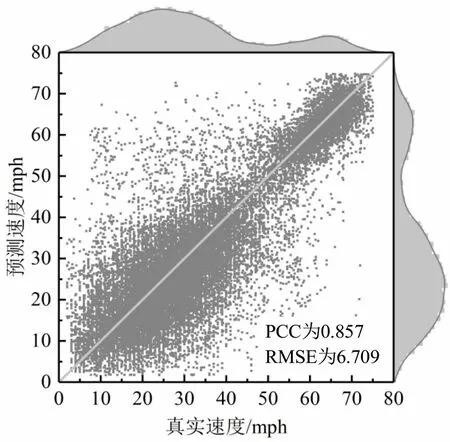
图5 早、晚高峰时期模型预测结果散点图Fig.5 Prediction performanceof GCN modelat peak hours
GCN模型考虑路网拓扑结构,图6和图7可视化这种相关性,颜色越深,表明该节点与其余节点越相关.图6为相关系数大于一定阈值的节点拓扑结构,以真实地理位置进行布局,可以发现模型和现实存在一定的匹配关系;节点代表每一条路段,节点大小和颜色代表与该路段有关联的路段数量,节点间的边代表两个路段之间的相关系数,越接近深色,相关系数越接近于1;不少路段与其他路段存在强相关性,通常为高速路的立交桥和主次干道的交叉口,这些路段在现实中也是对上、下游产生重要影响的关键节点.图7为所有节点的真实地理位置图,图7呈现出和图6相类似的结果.
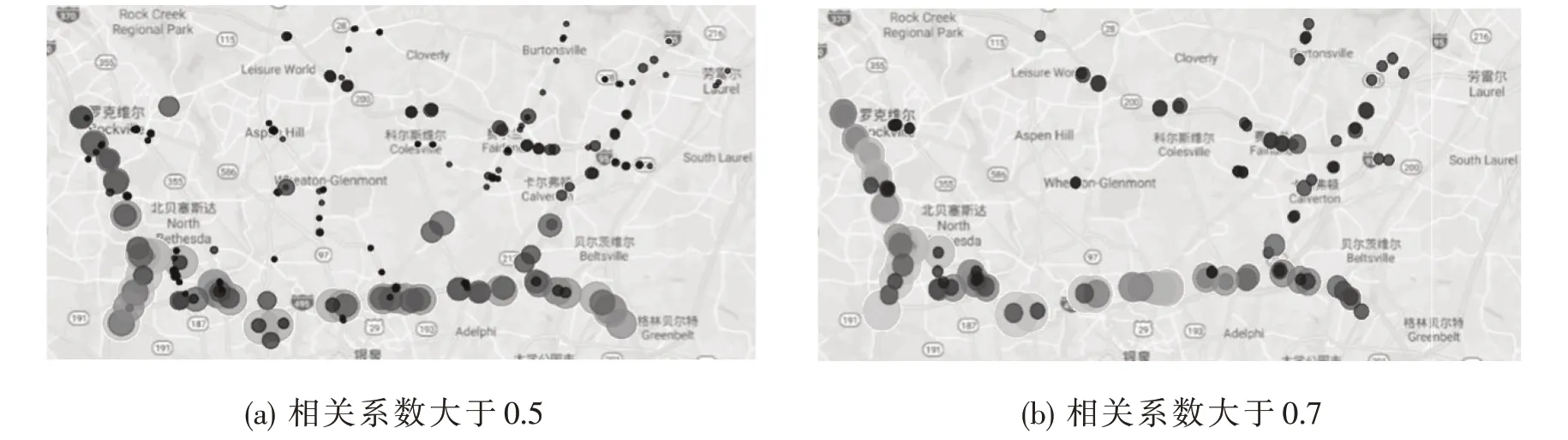
图6 相关节点拓扑结构图Fig.6 Graph topology of correlated nodes
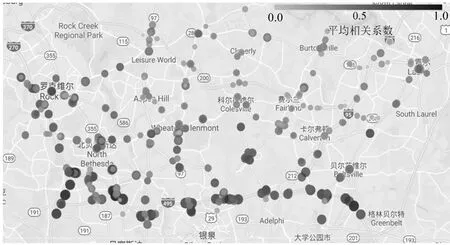
图7 各相关节点真实地理位置图Fig.7 Geographical layout of correlated nodes
4 结 论
本文提出用于路网交通流预测的GCN模型框架,采用真实大规模城市路网浮动车数据对GCN模型进行测试,通过实验确定合适的超参数,可视化路网各节点之间的相关性,并将这种相关性嵌入GCN模型框架中,利用GCN模型独特的邻接矩阵设计,使得模型同时考虑真实的路网拓扑结构和交通流的时空相关性,具有较高的预测精度、预测效率和现实解释意义.通过与现有模型进行对比发现,GCN模型在预测精度和计算效率上均有所提升,其中RMSE为5.012,MAPE为0.153.本文探究模型在多步预测下的预测结果,不同道路类型的预测结果以及早、晚高峰时段下的预测结果,GCN模型均具有较好的表现.GCN模型改进路网交通流预测框架,其高效和高精度特性为实际交通管控和路径规划场景应用奠定基础.后续研究可以在混合模型、超参数寻优等方面进行深入.
