城市干线短交织区元胞自动机多级换道决策模型
2020-09-01王玉婷谢济铭张媛媛
彭 博,王玉婷,谢济铭,张媛媛,唐 聚
(1.重庆交通大学a.山地城市交通系统与安全重庆市重点实验室,b.交通运输学院,重庆400074;2.昆明理工大学交通工程学院,昆明650224)
0 引 言
交织区是城市道路交通网络的重要构成部分,由于两股或多股同方向车流在有限长度范围内先后合流、分流,使得车流呈现高度紊乱状态.根据HCM 2010等文件中的术语规范,交织区长度一般不小于150 m,而在地形地貌等条件限制下,部分干道交织区长度明显小于150 m,行经车辆需要在更短的距离内进行跨越多条车道的复杂换道行为,这极易形成交通拥堵瓶颈.
为提高交织区交通通行效率,国内外学者对交织区交通运行特性展开了大量研究,例如,Marczak[1]建立了基于合流和分流叠加的高速公路交织区交通流模型;孙剑[2]探究了城市快速路交织区通行特征及影响因素,提出了通行能力模型.从更微观的视角来看,交织区特殊的交通流特性很大程度上源于复杂的换道行为,许多学者对此展开了较为深入的研究,例如:马新露[3]引入驾驶员性格参数和选择换道概率,建立了城市道路多路合流的元胞自动机模型;陈永恒[4]建立了快速路合流区车辆汇入的多次决策间隙选择模型;邓建华[5]构建了车辆状态更新次序随机的多车道换道模型;Yuan[6]基于驾驶模拟器的实验数据,研究了入口交织区和出口交织区连续变换车道时的强制换道行为;Xiang[7]引入动态换道概率,针对车辆换道强度过大等现象提出了改进的BL-STCA模型.
上述研究对高速路/快速路交织区[1-2]、合流区[3-4]等展开了换道行为建模分析,但对于多车道短交织区(交织区长度明显小于150 m,单向至少3车道的交织区构型)还较少进行针对性研究.此外,既有研究中的元胞自动机仿真测试[3,5,7]大都取元胞尺寸为7.5 m或5 m,步长为1 s,这对于复杂交织区车辆行为刻画的时空尺度及换道条件还不够精细;数据方面,也主要利用驾驶模拟器[6]、美国NGSIM[8]等展开研究,较难反映我国真实的车辆换道特征.
综上所述,本文针对典型城市干线多车道短交织区,利用无人机视频提取全样本高精度车辆轨迹数据(时间精度0.1 s、空间精度0.1 m),构建精细化的短交织区元胞自动机多级换道决策模型,并进行实测分析与模型对比验证.
1 模型构建
1.1 分区设置
采用分区建模的思想,形成三大分区,如图1所示.(1)上游,受交织区换道影响较小的上游区域,为分区Z1;(2)交织影响区域,交织区及受交织影响较明显的邻近区段,进一步划为分区Z2~ZN-1,为本文研究重点;(3)下游,受交织区换道影响较小的下游区域,为分区ZN.各分区Zk相对独立,分别构建其换道决策模型.

图1 多车道短交织区Fig.1 Multi-lane short weaving area
1.2 换道决策模型框架
考虑到上下游和交织影响区车辆行为及几何条件等差异性,建立换道决策模型框架如图2所示.对于跟驰行为,本文加速、减速、慢化过程与STCA模型[7]保持一致,并在位置更新时考虑了速度和位移小数部分影响[9].

图2 模型框架Fig.2 Model framework
一般而言,对于交织区研究范围的任意车辆,在保证安全的前提下均期望以更高的速度行驶.因此,车辆在行驶过程中,若与前车间距足够大,会首先考虑加速行驶;若与前车间距较小、可能追尾前车,则会考虑减速或换道.根据上下游和交织影响区车辆行为、交通流运行及几何条件等差异性,构建了图2所示的换道决策模型框架.
1.3 上下游换道决策模型
在上下游路段,车辆根据本车与邻近车辆的速度及间距,选择自由度更大的车道行驶,即行车更安全、车前和车后间距更大的车道.在交织区,换道过程包括生成换道动机、判断换道间距条件、目标车道后车速度更新三个阶段,对应变量符号如表1和表2所示.

表1 分区变量Table1 Zone parameters

表2 换道变量Table2 Variables for lane changing
(1)产生换道动机.
当车辆下一时步内行驶距离大于车前间距且速度比前车大,即满足式(1)和式(2)时,产生换道动机.

(2)判断换道间距条件.
判断车辆与紧邻前后车的安全间距是否满足向左自由换道间距条件,即式(3)和式(4),如果满足则进入步骤(3).
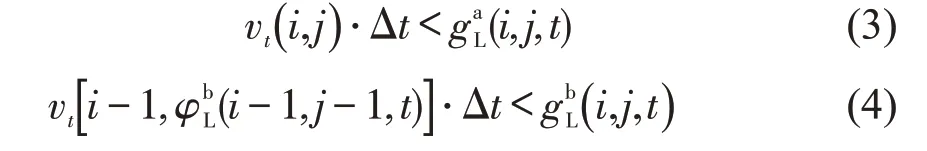
如不满足左侧换道间距条件,则判断是否满足右侧换道间距条件,即式(5)和式(6),如果满足则进入步骤(3).
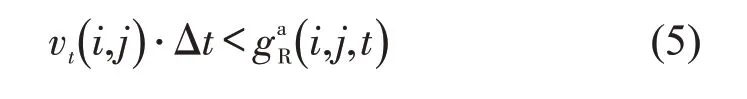
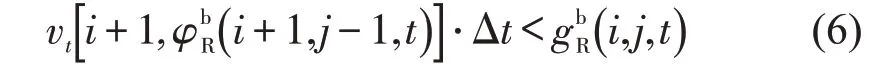
(3)目标车道后车速度更新.
当车辆满足换道动机和向左换道间距时,考虑换道车辆与目标车道后车的速度差及安全间距,向左换道并更新后车辆速度,即

式中:为车辆(i,j)换道后速度,根据ξk进行随机慢化而得.
当满足换道动机和向右换道间距时,向右换道并更新后车辆速度,即

1.4 交织影响区多级换道决策模型
对于城市干线多车道短交织区,车辆需在有限距离内换至目标车道,为了汇入主线或驶入匝道,可能采取减速、低速甚至停车换道等风险较高的行为,以增加换道决策机会及成功换道几率.为有效描述短交织区复杂的换道行为机理,根据多级决策理论[10]主要构建了两阶段换道决策过程,即换道时机决策阶段和换道概率决策阶段.换道时机决策阶段基于安全风险建立了自由型、风险型、强制型等5类逐级决策过程;换道概率决策阶段建立了基于概率的换道行为3步决策过程.
(1)根据车速、间距及汇入汇出比例,判断换道需求.
当车辆行驶受阻,即满足式(9)和式(10)时,产生换道动机.
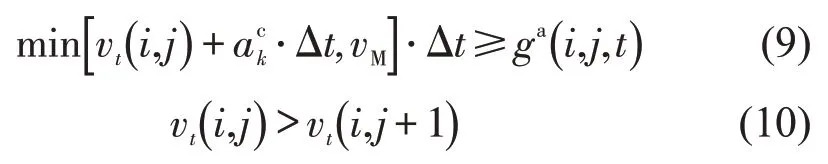
相比上下游区域,车辆在除了寻求更快的通行速度与更大的行驶空间外,还具有汇入汇出主线的路径转换需求.因此,在换道需求规则中,增加考虑了汇入主线和驶入匝道的需求因素.
当车辆(i,j)位于主线时,如果满足式(11),产生汇入匝道需求.

式中:rand(0,1)为0~1之间的随机数.
当车辆(i,j)位于匝道,如果满足式(12),产生汇入匝道需求.

(2)确定换道时机.
针对车辆换道间距、车辆轨迹等数据统计分析发现,交织区车辆换道时面临的安全风险可分为自由型、风险I型、风险II型、强制I型、强制II型5类,其安全风险依次递增.车辆会以安全风险较低为目标实施换道,根据换道强度及安全风险由低到高进行逐步决策.具体如下:
①自由型换道.本车与目标车道前后车的速度差较小、车间距较大,可保证换道时本车和前后车均安全,此时可安全换道,即满足式(13)或式(14)时,进入步骤(3).
向左换道为

向右换道为

②风险I型换道.本车与目标车道前车间距较小、与左后车间距较大,存在追尾左前车的风险,但本车可控制追尾风险,即满足式(15)或式(16)时,进入步骤(3).
向左换道为
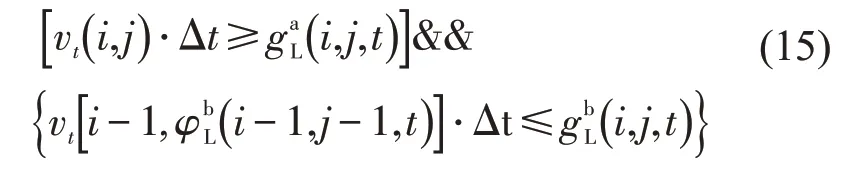
向右换道为

③风险Ⅱ型换道.本车与目标车道前车间距较大、与后车间距较小,存在被目标车道后车追尾的风险,此时本车较难控制被碰撞风险,安全风险略高于风险I型换道,即满足式(17)或式(18)时,进入步骤(3).
向左换道为

向右换道为

④强制I型换道.本车与目标车道前后车辆间距均较小,此时强行换道将与前、后车辆有较大碰撞风险,安全风险明显高于风险II型换道,即满足式(19)或式(20)时,进入步骤(3).
向左换道为

向右换道为

⑤强制II型换道.当车辆处于交织区末端或路况不熟悉等情形下,可能会低速甚至停车伺机换道,此时换道不仅受目标车道前后车辆碰撞风险,还存在被本车道后车追尾风险,安全风险高于强制I型换道,即满足式(21)或式(22)时,进入步骤(3).
向左换道为

向右换道为

据此,可反映短交织区车辆逐步决策选择换道时机的过程,模拟车辆复杂换道行为.
(3)车辆根据向左和向右的换道概率,构建3步决策过程,确定是否换道.
2 数据采集
在高峰时段利用无人机拍摄典型多车道短交织区(交织区长度约70 m)交通视频,提取车辆轨迹2 912条,时间精度0.1 s、空间精度0.1 m.据此提取速度、加速度、车辆跟车间距、密度、换道信息等.
换道信息包括车辆换道位置及方向,是本文的关键数据.采用高阶多项式拟合路缘线函数f(xr)、车辆轨迹函数f(xc),识别f(xr)与f(xc)交点即为换道点,如图3所示,据此计算换道次数.对于换道方向,若f(xc)在换道点的一阶导数大于0,车辆向北换道,否则,向南换道.
3 仿真验证
3.1 参数设置
本文元胞自动机模型采用开放式边界条件,按实测到达率产生车辆进入仿真路段,并细化了元胞尺寸及时间步长,主要参数见表3.为消除暂态影响,根据10 000~13 600时步的运行结果计算所需区域的平均速度、平均流量、平均密度等.
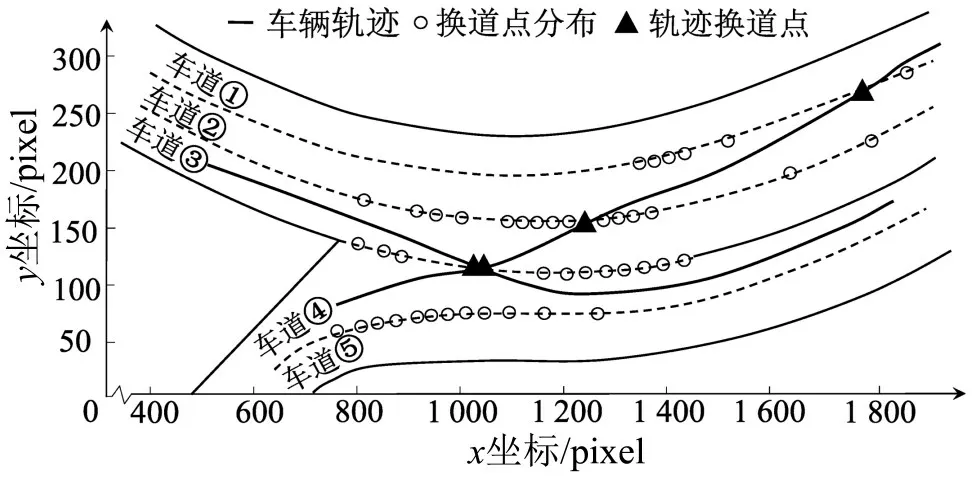
图3 换道信息提取Fig.3 Lane changing feature extraction

表3 元胞空间参数Table3 Parameters of automata space
根据实测车辆间距及微观轨迹数据统计分析,将研究范围划为6个分区,标定和设置分区与未分区建模的参数值,如图4和表4所示.

图4 研究范围分区Fig.4 Zoning strategy of research area
3.2 模型效果分析
本文提出分区建模的交织区多级换道决策模型(模型IV),构建了3个对比模型:未分区换道模型(模型I,可模拟交通特性差异不大的交织区)、分区STCA换道模型[7](模型II,多用于模拟单侧换道问题)、分区多路合流换道模型[3].(模型III,可模拟城市多路合流交织行为),并从流量、时空轨迹、换道规律等方面进行分析.
3.2.1 流量分析
统计实测平均车道流量及各个模型10 000~13 600时步的平均车道流量,对比情况如表5所示,可以看出:①对于平均车道流量,模型I相对误差为38.69%,模型II~模型IV相对误差分别为5.14%、5.02%、1.64%,表明分区建模的3个模型更符合实测数据,本文模型最接近实际值;②从车道流量的分布情况来看,在[±200]范围内,模型I~模型IV 流量占比依次为22.89%、87.69%、87.63%、88.19%,表明考虑分区的模型流量更集中在真实流量附近,未分区的模型I 流量偏大,集中于[1 056,2 000],表明分区建模效果更优.

表4 模型变量取值Table4 Model variable values
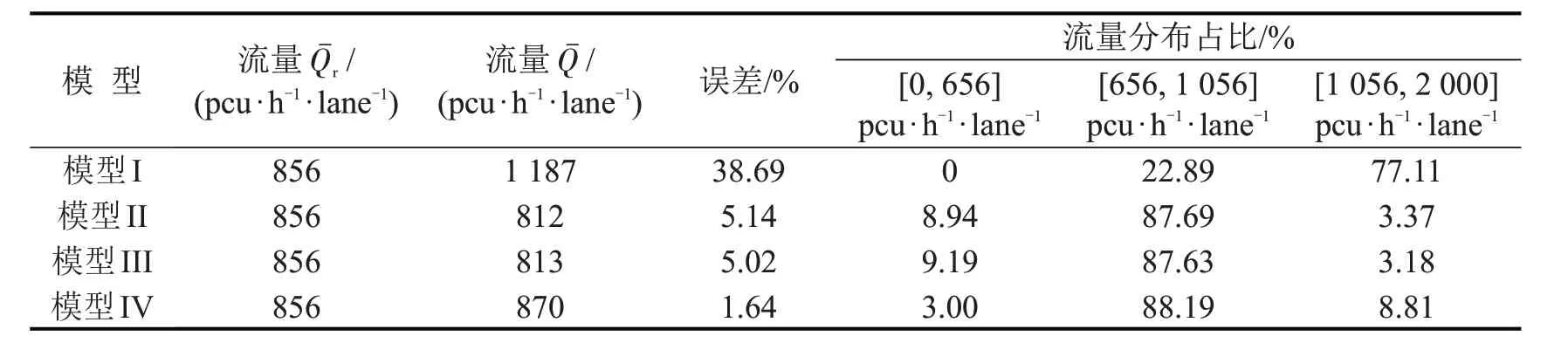
表5 模型流量对比Table5 Traffic volumes comparison among models
3.2.2 时空轨迹图分析
以交织特征最显著的车道3为例,绘制车辆时空轨迹,如图5~8所示,可以看出:(1)模型I时空轨迹在交织区Z3~Z4区域突变明显,堵塞现象较为严重,交织影响区上游与下游速度差异较大,且上游速度明显偏低;(2)模型II时空轨迹在交织区Z3~Z4较为平稳连续,交织影响区上游速度比下游速度略低,交织区堵塞现象不太明显,但在交织区末端时空轨迹发生骤变,与实际交通运行情况不符;(3)模型III时空轨迹变化较为连续顺畅,在交织区Z3~Z4附近未体现出频繁加减速、换道等带来的瓶颈效应;(4)模型IV时空轨迹在交织影响区域上下游Z2、Z5变化较为连续,上游速度略小于下游,同时在交织区Z3~Z4范围具有轨迹紊乱、轨迹线不连续的现象,体现了车辆相互干扰较大、换道频繁等特性.总体上,分区后的模型可更好地反映交织区交通流特性,体现出换道交织带来的渐变瓶颈效应.

图5 模型I时空轨迹Fig.5 Space-time trajectories of model I
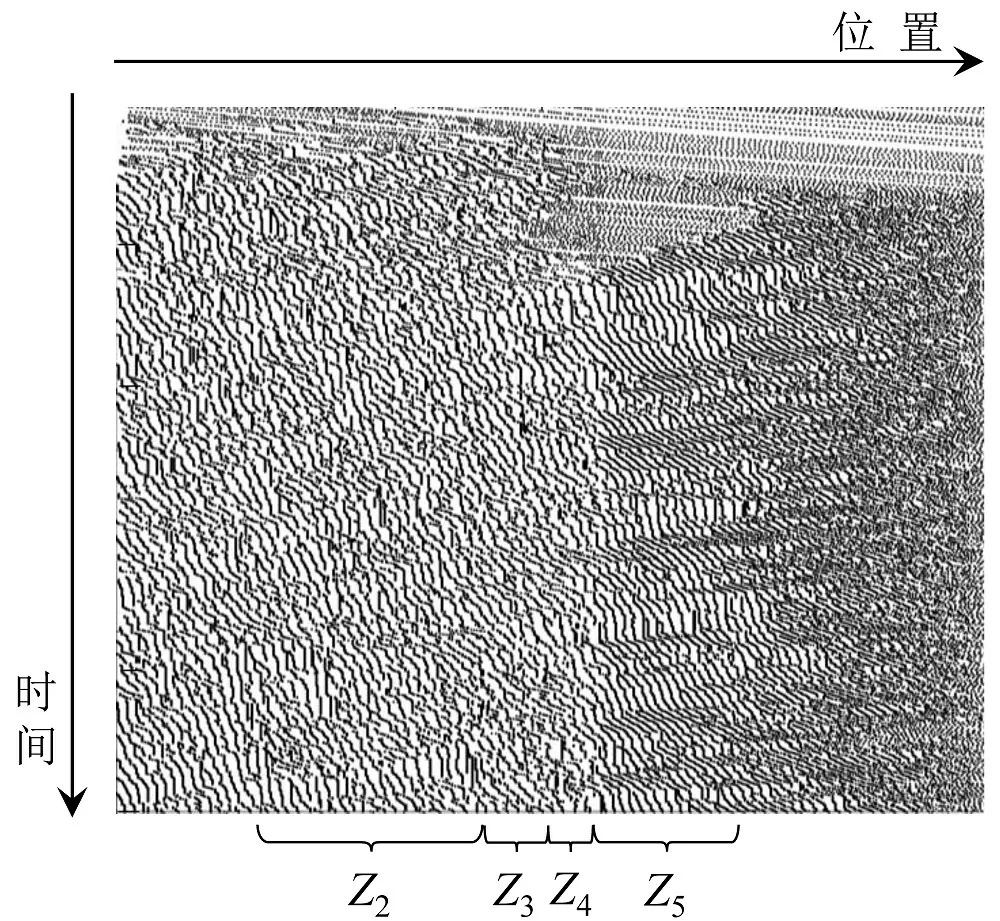
图6 模型II时空轨迹Fig.6 Space-time trajectories of model II
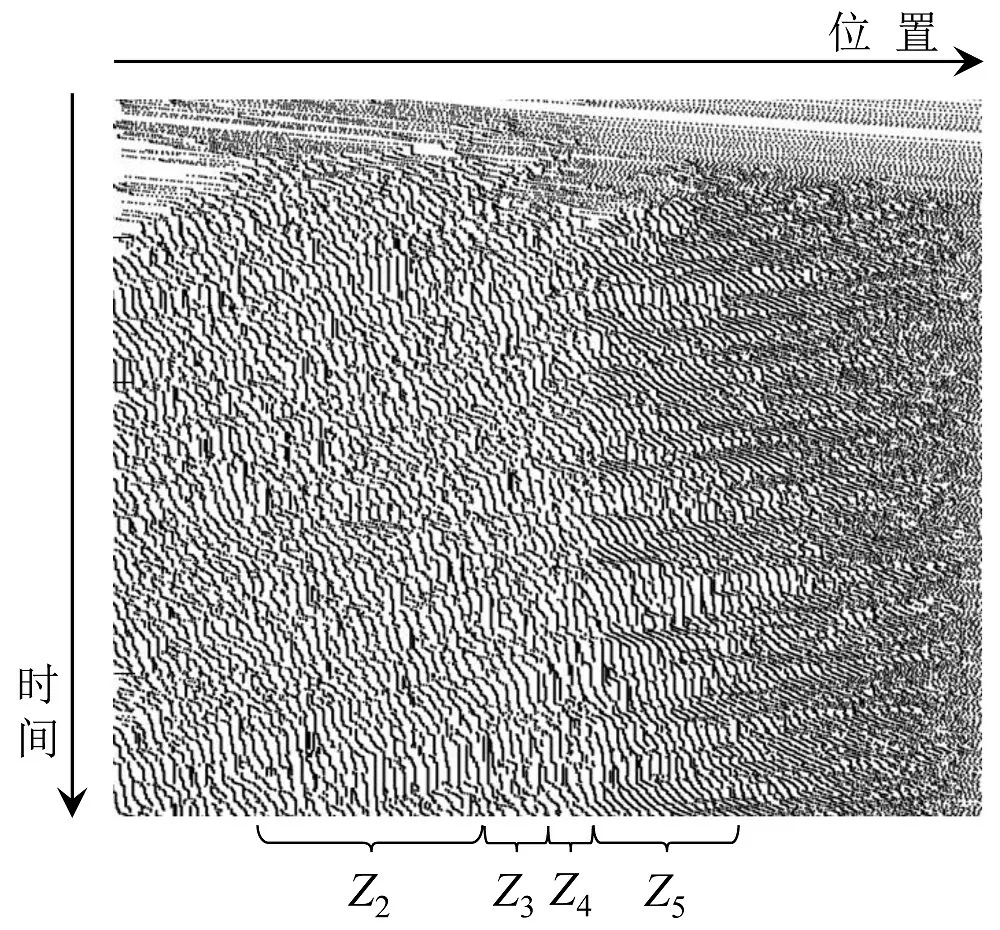
图7 模型III时空轨迹Fig.7 Space-time trajectories of model III

图8 模型IV时空轨迹Fig.8 Space-time trajectories of model IV
表6展示了交织影响区Z2~Z5的车速对比情况,可以看出:(1)模型I~模型IV平均速度误差依次降低,说明分区建模可有效提升仿真准确性;与模型II~模型III 相比,模型IV 速度误差有所减小,说明换道决策细化程度越高,仿真结果越符合实际情况;(2)对于Z2、Z3~Z4的平均速度,优劣排序依次为模型III、模型IV、模型II、模型I,模型III对合流区车辆行为模拟较好、模型IV与模型III效果相近;对于Z5,模型IV平均速度误差最低(3.89%),显著优于模型I~模型III(15%~40.56%).总体上,经分区建模及决策细化后,可较好地反映各分区速度差异,刻画车辆行经合流区Z2、交织区Z3~Z4、分流区Z5的速度特性.

表6 车辆速度对比Table6 Vehicle speeds comparison
3.2.3 换道规律分析
本文交织区车道4和车道5均为匝道,可考虑为一个整体,暂不讨论二者之间的换道规律,表7统计了其余情形下在10 000~13 600时步的换道次数及误差,其中,模型IV-A、IV-B、IV-C仅换道间距条件与模型IV有所区别:模型IV-A只保留模型IV的自由型与风险Ⅰ型换道条件;模型IV-B在模型IV-A 上加入风险Ⅱ型换道条件;模型IV-C在模型IV-B基础上加入强制Ⅰ型换道条件.
可以看出:(1)模型II、模型III 换道次数平均误差显著高于模型I,说明单独开展分区建模并不能很好地模拟交织区换道情形,还有必要细化考虑换道决策行为;(2)随着模型IV-A、模型IV-B、模型IV-C、模型IV换道决策条件的不断补充,换道次数越来越接近实际值,最终模型IV平均换道次数误差最低,说明精细化的换道规则可有效模拟交织区复杂的换道决策行为过程及结果.
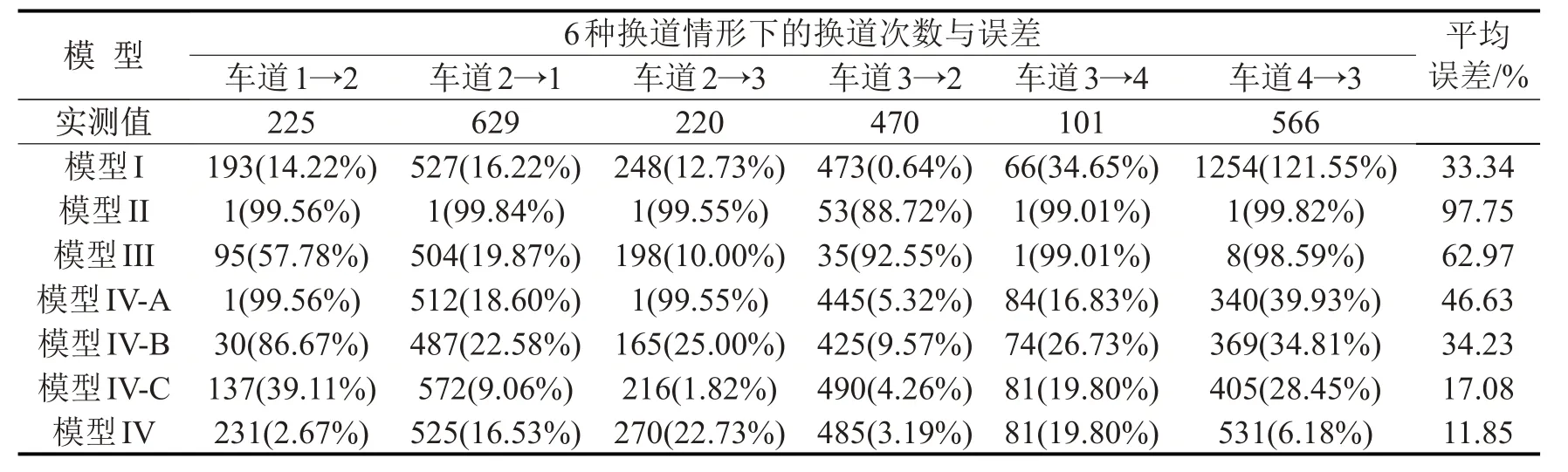
表7 换道次数对比Table7 Lane changing times comparison
4 结 论
本文针对城市干线多车道短交织区,利用无人机视频提取车辆微观轨迹及速度、加速度等交通参数,基于分区建模思想构建了上下游换道决策模型、交织影响区多级换道决策模型.测试表明,本文模型在流量分布、速度分布及换道次数分布等方面均与实际情况比较一致,可有效刻画复杂交织影响区域车辆跟驰及换道决策行为特性.
本研究可细致描述多车道短交织区的复杂换道决策行为,为交织区交通运行评估、通行能力测算及优化管控等提供理论与方法支持.由于交织区交通环境复杂多样、驾驶行为各异,后续研究可进一步增加实测数据、考虑驾驶员特性等,提升模型精度及适用性.
