高中数学主题教学研究热的冷思考

【摘 要】在《普通高中数学课程标准（2017年版）》颁布之后，主题教学成为高中数学教学研究的热点话题。通过近几年的文献分析，研究者发现对内容的深度分析、对情境的合理创设、对“教、学、评”一致性的研究，是当前高中数学主题教学研究中尚未妥善解决的问题，也是需要思考的重要课题。

【关键词】主题教学;内容分析;情境创设;“教、学、评”一致性

【作者简介】任念兵，高级教师，新青年数学教师工作室创始成员，主要研究方向为高中数学课堂教学与命题研究。

【基金项目】上海市浦东新区2018年教育科学研究项目重点课题“基于高中数学核心素养的中观教学设计与实践研究”（A201806）

史宁中教授认为，要落实培养学生数学核心素养的教育目标，至少应当遵循两个原则：一是把握数学知识的本质，二是设计并且实施合理的教学活动。教材编写和教学设计都应充分关注这两个原则。由于数学内容很难通过一节课或一个知识点就把数学的本质表述清楚，因此，在教学设计中，应当把一些具有逻辑联系的知识点放在一起进行整体设计[1]。这个数学教学观点，也就是《普通高中数学课程标准（2017年版）》（下文简称《课程标准》）在教学实施建议中所倡导的整体教学观，主题教学设计正是落实整体教学观的课堂教学实施方案。

主题教学与单元教学、项目学习、深度学习的含义一致（本文统称为主题教学），是相对课节教学而言的，就是从关注一节课、一节课的教学到关注更大范围（如一个单元、一章、一个主题）的教学[2]253-260。类似的提法还有结构化设计、中观设计、学材再重构等，都是着眼于大立意、大情境、大任务、大问题，从关注零散的知识点到关注系统的“知识团”，从碎片化教学走向整体教学。

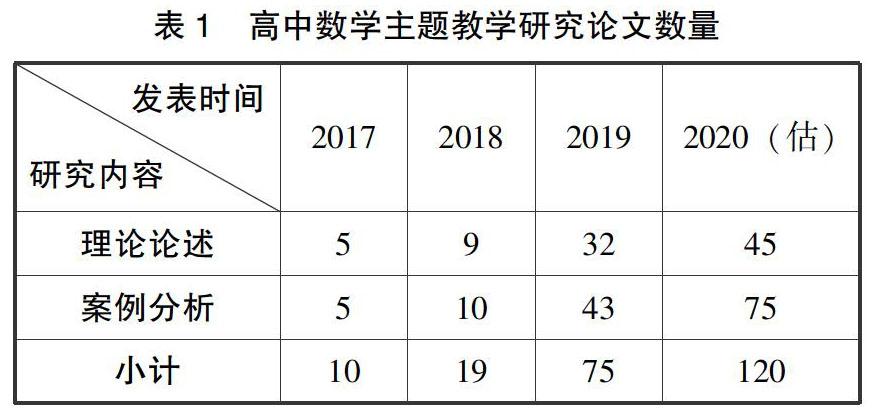
《课程标准》颁布以来，主题教学在一线教师群体中逐渐形成了较为广泛的理念认同，并呈现出如火如荼的研究态势。笔者在中国知网（CNKI）数据库中以篇名含“单元”或“主题”，以及全文含“数学”为检索条件进行搜索，再逐篇筛选出关于高中数学主题教学的论文。其中，将针对某个具体主题进行论述的文章归入“案例分析”类，泛论主题教学的特征、原则等内容的文章归入“理论论述”类。笔者在撰写本文时，由于只检索到2020年1—4月发表的论文，因此将篇数乘以3作为2020年论文数的估计值，统计情况见表1。虽然“单元教学”的提法在20世纪90年代就已经广泛流传开来，但是在高中数学教学领域以“主题”“单元”结构进行整体设计的研究是近几年才开始的，较早发表且具有代表性的论文是2016年吕世虎等发表的《单元教学设计及其对促进数学教师专业发展的作用》。高中数学主题教学的研究论文从2017年开始大幅度地逐年增长，其中有4篇是师范大学的硕士论文。

数学教育类期刊也为主题教学研究热“推波助澜”。例如一些期刊进行“单元教学设计”专题征稿，或者举办“单元—课时教学设计征文大赛”等。近几年中国人民大学复印报刊资料《高中数学教与学》策划主题教学专题，介绍教育教学的研究成果，例如该杂志2018年第12期、2020年第4期刊登有关“单元教学”的文章，2018年第7期、2019年第1期、2020年第1期刊登有关“深度学习”的文章等。各地教研机构也在大力支持和推動主题教学的研究，以“主题教学”“单元教学”为研究内容的省、市级教育科学规划课题如雨后春笋般涌现;上海市教育委员会教学研究室还专门组织人员编写了《高中数学单元教学设计指南》（人民教育出版社，2018），等等。

基于课程标准解读[2]253-260和主题教学论文的研究，笔者就当前主题教学的研究热做一些冷思考，与正在研究主题教学的同行们探讨。

一、对数学内容的深度分析是主题教学成败的关键

理解数学是教师教好数学的前提，从中学数学学科的整体结构、核心内容和重要思想上整体把握和认识数学教学内容，是主题教学研究的首要工作。

注重对教学内容的理解和把握是我国中学数学教师的优良传统，尤其是改革开放以来，涌现出一大批对数学内容解读有创见、教学成绩突出的优秀教师，他们总结出不少教学名言和教学主张。例如北京的孙维刚老师倡导结构教学法，提出“八方联系、浑然一体、漫江碧透、鱼翔浅底”的教学主张，注重新旧知识之间的联系，站在系统的高度把握数学的结构;江苏的李庾南老师践行“自学、议论、引导”教学法近40年，曾荣获首届（2014年）基础教育国家级教学成果奖一等奖，而其成功的秘诀之一就是整体理解教学内容的“学材再重构”;上海的曾容老师强调在教学中要弄清楚“是什么、为什么、还有什么”的问题。“是什么”是追寻数学学科的内在逻辑，研究脉络和研究方法是什么;“为什么”是追问概念、公式的内在动因，为什么要研究这些概念和公式;“还有什么”是追溯核心问题的历史踪迹（纵向联系），追求数学知识的通透理解（横向联系），等等。因此，主题教学具有广泛的实践基础和深厚的历史积淀，当前的主题教学研究在一定程度上是对优良传统的继承、发扬和深化。另一方面，回归学科是近年来国际数学教育界的主流话题和趋势，MPCK、MKT等数学学科教学知识的研究自从20世纪末引入我国后，对数学内容的深度理解成为很多教师的专业追求。因此，优良传统和外来理念的叠加，使得主题教学经《课程标准》的倡导之后，得到了一线教师积极的响应。

主题教学基于对数学内容的整合，对教师理解数学的能力提出较大的挑战。主题教学要求教师具备较高的数学元认知水平，能够对数学理论体系具有广泛的了解，具有用高观点解释初等数学的能力;能够梳理主题（单元）的逻辑脉络（章建跃博士称为数学研究的“基本套路”），并能洞察显性知识背后的隐性知识（又称“默会知识”）。所以，教师能否深度分析数学教学内容，是决定主题教学成败的关键。

比如，在“数列”的主题教学中，教师可以对“等比数列前n项和”做如下“瞻前顾后”的剖析。

（1）“瞻前”分析——为什么不能类比等差数列前n项和公式的推导方法来研究等比数列求和？从形式上看，等差数列前n项和公式的推导方法（倒序相加法）不能简单地类比到等比数列中来。但是等差数列、等比数列求和都是通过消去相同的项，使得和式中的项数减少：等差数列求和的倒序相加法Sn+Sn，实际上是通过“配对”将不同数的和转化为相同数的和，从而减少项数;等比数列求和的方法除了错位相减法（教材选择的方法），还有迭代递推、利用合分比定理、裂项相消等方法。它们都合乎消项的逻辑，但是不太利于类比等差数列求和的思路。Sn-qSn则是通过“错位”消去两式中的公共项，从而减少项数。因此，这些数列求和的方法看似形式不同，但本质上都是通过运算技巧达到消项的目标。

（2）“顾后”分析——如何理解等比数列求和的思想方法对后续学习的价值。从思想内涵上看，数列求和的本质是消项。数列是离散的函数，而连续函数的定积分，根据牛顿-莱布尼茨公式，可以求出原函数后作差，因此从运算技巧上看，数列求和的根本方法是“裂项相消”（差分求和）。等差（比）数列的求和都可以利用适当的裂项技巧来实现相消。在历年的高考数学压轴题中，数列不等式a1+a2+…+an

又如，在“圆锥曲线”的主题教学中，教师可以对“圆锥曲线的性质”做如下纵横联系的剖析。一般地，研究圆锥曲线性质的思路为整体性质→局部特征→与系统环境的关系。整体性质是指圆锥曲线体现出的整体特征，包括对称性、顶点、范围等;局部特征是指圆锥曲线相关要素体现出的特征，比如圆锥曲线上的点与焦点构成的线段（三角形）的性质等;与系统环境的关系是指圆锥曲线与其他曲线的位置关系，典型的问题是圆锥曲线与直线的位置关系，圆锥曲线中某些特殊弦的研究都可以归入这类关系中。椭圆、双曲线、抛物线性质的研究也都遵循这样的研究思路。

相较于教材章节主题，跨章节的主题教学设计，对教师深度分析、整合数学内容的能力提出了更高的要求。从目前已发表的论文来看，涉及跨章节主题基本只有《课程标准》中介绍的“函数单调性”（案例36），鲜见其他跨章节主题的研究。这从另一个侧面说明，整体把握数学内容对于主题教学研究的重要性。

章建跃博士认为，教师对课程内容的理解水平不高，在挖掘数学内容蕴含的育人价值方面缺乏意识和能力，是当前教学设计出现偏差的主要原因[3]。倘若教师缺乏一定的数学元认知能力，那么在主题教学设计中就只能停留在数学内容的表面理解上，在内容分析时依然是堆砌零散的点状知识而不能整合为“知识团”。无论教学设计的外在包装是表格还是所谓的“思维导图”，只要教师不能挖掘内容背后的隐性知识，都将无法帮助学生整体把握内容，不可能真正实现思维的可视化。

就当前高中数学主题教学研究的相关论文来看，深度分析数学内容的文章较少，浮于表面的空泛议论偏多;甚至有“蹭热点”的文章“用新瓶装旧酒”“穿新鞋走老路”，离主题教学的要求相差较远，这是值得有志于主题教学研究的同行们思考的问题。

二、对问题情境的合理创设是主题教学实施的要素

哈尔莫斯说：“问题是数学的心脏。”在数学的发生和发展过程中，问题可以分为两类：一类是促使概念、原理、理论产生的原始的问题，哲学上称为“本原性问题”;另一类是在理论发展过程中派生出来的与自然科学没有直接关系的问题，称为“派生性问题”[4]。任何重要概念、定理的产生都有其背景、根源，这些问题既有可能是本原性的，也有可能是派生性的，它们都可以作为驱动中学数学课堂的问题载体，也是主題教学设计的问题来源。

主题教学重在对内容的深刻把握，但有些隐性知识并不适合“告知”学生，教师需要设计适当的问题串来帮助学生理解知识，于是问题的选取就成为难点所在。因此，合理创设问题情境是主题教学顺利实施的关键。另外，主题教学仍然要通过课时教学去落实，而在每个课时的具体教学过程中，教学流程、方法手段和技术手段等，与过去的课时教学相比并没有实质性变化，最大的区别体现在对教学内容的整合与设计上，因此整合内容、设计主题问题是凸显主题教学特点的重要一维。

在主题教学中创设问题情境，应尽量选取可以在多个课时使用的较为综合性的情境素材，设计主题系列学习活动（问题串），使整个主题的教学显得更为连贯。比如在“数列”主题教学中，谢尔宾斯基三角形就是值得尝试的主题问题。在数列概念引入、等比数列、递推数列、数列求和等课时教学中，教师都可以围绕谢尔宾斯基三角形来创设问题情境。

问题情境的创设没有一定之规，不能生搬硬套，不同类型的数学内容需要用不同的方式来处理，或娓娓道来，或开门见山，或引发认知冲突，或利用逻辑演绎。比如，从具体的例子出发，可以归纳出一般结论、引发猜想，可以打开思路、引出证明，因此从特殊到一般是创设问题情境的常见思路。然而，事物往往具有两面性，在中学数学中也常常会有这样的问题，即抽象、一般的情形可能比具体、特殊的情形更直观、更容易解决，“点到直线的距离”即为一例。很多教学设计类论文在设计“点到直线的距离”课例时，都是先给出直线的方程（系数给定）和直线外一点的坐标，然后求点到直线的距离，试图通过特殊问题的解决寻找一般的思考路径。但实际上，相对于字母表示形式，具体系数形式的直线方程和点的坐标，对于该问题的解决并不能起到简化和启迪思维的作用，两者在思维量上是没有任何本质差异的，有时候具体数字的特殊性反而可能会导致思路的异化（特殊系数下的特殊直线会产生特殊解法）。着眼于“直线与方程”的主题设计，教师可以从内容的内在逻辑联系上开门见山地创设“点到直线的距离”的教学情境，并提出问题，教学片段如下。

师：在解析几何中，用代数方法研究几何对象，用方程表示直线后，通过方程研究两条直线的位置关系——相交、平行和重合。对于相交直线，我们可以定量研究它们的夹角;若两条直线平行，如何定量刻画两条直线的位置关系？

生：用距离定量刻画两条平行直线的位置关系。

师：由于两条直线平行时，一条直线上任意点到另一条直线的距离即为两条平行线之间的距离，因此我们将研究点到直线的距离。

《课程标准》提出，情境创设和问题设计要有利于发展学生的数学学科核心素养，教学情境包括现实情境、数学情境、科学情境，每种情境又分为熟悉的、关联的、综合的。对于主题教学而言，在问题情境创设方面，应着重研究关联的、综合的情境。为高中数学的每个教学主题配套主题问题，这也是需要广大同行冷静思考的系统化工程。

三、对“教、学、评”一致性的思考是主题教学研究的归宿

《课程标准》在实施建议中，不仅提出了“教”的建议，倡导主题教学，而且提出了“重视学”的要求，要求教师把教学活动的重心放在促进学生学会学习上，积极探索有利于促进学生学习的多样化教学方式，丰富作业的形式，提高作业的质量，提升学生完成作业的自主性、有效性。同时，《课程标准》还提出了评价建议、高考命题建议等。“教”“学”“评”构成了教学的完整闭环，主题教学对培育学生的数学核心素养是否有效，也应从“教、学、评”一致性角度进行研究。

对应主题教学，教师可以考虑围绕核心概念或重要方法的“知识团”来命制创新试题，力图让那些注重整体理解数学、把握数学本质的学生能够考出高分，而舍本逐末不求甚解，埋头刷题、大搞题海战术的学生则“望题兴叹”。倘若真能做到这一点，以高考引导教学，以评价来撬动教育改革之锚，主题教学才能真正落实、深入人心，核心素养才能真正落地、遍地开花。

比如，在教学中，教师可以围绕中学数学中的“距离”概念，梳理概念的内涵和外延，沟通初高等数学中距离概念的本质，在高三复习课上设计“距离”主题教学[5]，并相应地配备考查学生对距离概念深度理解的创新题（参见《课程标准》案例23距离问题），检验主题教学的效果。

除了配合主题教学的“评价”研究，有关“学”的研究还比较少，在已发表的论文中，笔者只看到过一篇《高中数学单元作业设计与实施》（李家齐，2019）涉及主题教学中如何“促进学生学会学习”。思考“教、学、评”的一致性，是主题教学亟待研究的重要课题，也是值得同行们冷静思考的第三个问题。

系统的力量在于“整体大于部分之和”，主题教学着力于挖掘数学内在的系统的力量，因而能有效地提高教学效率。当前，高中数学主题教学的研究方兴未艾，广大一线教师以饱满的热情对主题教学进行教学实践和设计研究，而在“教研成果”大量涌现的繁荣、热闹的背后，对教学内容的深度分析、對情境的合理创设、对“教、学、评”一致性的研究等问题，正摆在主题教学研究者面前，需要我们静下心来，在理解教学、理解数学、理解学生上下大功夫才能妥善解决。

参考文献：

[1]史宁中，林玉慈，陶剑，等.关于高中数学教育中的数学核心素养：史宁中教授访谈之七[J].课程·教材·教法，2017（4）：8-14.

[2]史宁中，王尚志.普通高中数学课程标准（2017年版）解读[M].北京：高等教育出版社，2018.

[3]章建跃.数学学习与智慧发展[J].中学数学教学参考，2015（19）：4-10.

[4]曹广福，张蜀青.问题驱动的中学数学课堂教学（理论与实践卷）[M].北京：清华大学出版社，2018.

[5]任念兵，汪健.刍议在高三复习课上“玩概念”：以“距离”概念为例[J].数学通报，2015（7）：27-29.

（责任编辑：陆顺演）