HPM视角下的“扇形的面积”同课异构课例分析

2020-08-31王海雯汪晓勤

中小学课堂教学研究 2020年8期

王海雯汪晓勤

【摘要】扇形的面积直接应用于圆锥的侧面积和全面积的计算，为学生到高中进一步学习立体几何打下基础。研究者以HPM视角下的“扇形的面积”同课异构为课例研究，从宏观和微观两个层面，对教师A和教师B的教学进行比较和分析，关注知识的发展过程和学习的上升过程，希望学生经历概念的形成过程和公式的生成过程，自然地推导出扇形的面积公式，既符合学生的认知规律，又能引导学生领会其中的数学思想和方法，从而使教师获得有益的教学启示，并为HPM课例研究提供参考。

【关键词】HPM;扇形的面積;同课异构

【作者简介】王海雯，华东师范大学教师教育学院在读硕士研究生，主要从事数学史与数学教育研究;汪晓勤（本文通讯作者），华东师范大学教师教育学院副院长，教授，博士生导师，主要从事数学史与数学教育研究。

【基金项目】上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地项目“数学课程与教学中如何落实立德树人研究”（A8）

一、引言

“扇形的面积”是沪教版数学六年级第一学期第四章“圆和扇形”第2节的内容（[DK]“弧长和扇形面积”是人教版数学九年级上册的内容）。扇形的面积直接应用于圆锥的侧面积和全面积的计算，为学生到高中进一步学习立体几何打下基础。在学习本知识之前，学生已经具备了弧长、圆心角、圆的周长、圆的面积等基本公式的几何基础知识，能计算一些与圆有关的简单组合图形的周长和面积。教科书首先以生活中学生熟悉的三色陀螺引入，通过观察红色、黄色、蓝色部分的形状，引出扇形的概念。接着，通过思考扇形面积与哪些量有关，教师引导学生推导出扇形面积公式。一般地，推导扇形面积公式主要有以下两种方法：一种是通过探究弧长、圆心角、扇形占圆中相应量的几分之几，由部分与整体的关系推导出扇形面积公式;另一种是通过求特殊角的扇形面积来探究扇形面积公式。[1-2]

HPM视角下的数学教学关注知识的发展过程和学习的上升过程，希望学生经历概念的形成过程和公式的生成过程，自然地推导出扇形面积公式，既符合学生的认知规律，又能引导学生领会其中的数学思想和方法。目前的教科书以及已有的教学设计是从扇形和圆的面积比例关系得到扇形面积公式，但并未将推导圆面积公式的方法用于扇形，导致扇形面积公式S=1/2lr不易被学生理解。因此，笔者希望通过将数学史融入扇形面积的教学来解决以上问题。

为此，HPM工作室以“扇形的面积”为课题开展课例研究，来自上海市两所不同学校的教师A和教师B各自实施了“扇形的面积”的教学。在课例研究的第一个环节，两位教师首先搜集了19世纪西方早期教科书中关于“扇形的面积”的教学内容，从扇形的定义和扇形面积公式的引入、推导和应用等方面，挖掘有用的史料;其次，教师研读这些史料并对其进行裁剪和加工，结合教材和学情，各自完成教学设计;再次，经过HPM工作室的研讨，两位教师对教学设计进行修正;最后，根据两位教师试讲的效果，HPM工作室对教学设计再次做出修正和完善，并付诸实践。

本文从宏观和微观两个层面对教师A和教师B的教学进行比较和分析，揭示两节课的特点，使广大教师从中获得有益的教学启示，并为HPM课例研究提供参考。

二、扇形面积的历史素材

（一）扇形的定义

扇形是初中平面几何的重要概念之一，现行各版本的初中数学教科书所给出的扇形定义都不同。人教版和沪教版给出的扇形的定义是从圆心角出发，而北师大版、苏教版和浙教版给出的定义则是从一条弧出发。历史上，最早给出扇形定义的是古希腊数学家欧几里得（Euclid）。他在《几何原本》卷三命题10中给出了扇形的定义：由顶点在圆心角的两边和该两边所截一段圆弧所构成的图形，称为扇形。沪教版和人教版的教科书对扇形的定义是由组成圆心角的两条半径和圆心角所对的弧围成的图形。而在西方早期的教科书中，扇形的定义却不尽相同。除了与《几何原本》相似的定义，大多数的美英早期教科书也倾向于把扇形定义为：一条弧和经过这条弧两端的两条半径所围成的图形。北师大版、苏教版和浙教版教科书中的定义与此相同。

（二）扇形面积公式的推导

第一类是分割法，如美国数学家华尔克（T.Walker）在《几何基础》中即采用此法[3]。由于圆的周长可看作是边数趋于无穷的正多边形的周长，内接圆的半径就是它本身的半径，而边数趋于无穷的正多边形可分割成无穷多个近似的小三角形，三角形的面积为底乘以高除以2，因而圆面积等于周长的一半乘以半径。类似地，将扇形分割成无穷多个小三角形，那么扇形面积等于弧长的一半乘以半径。如图1，将扇形分成无限个小扇形，将每个小扇形看作近似三角形，于是扇形面积等于无限个三角形面积之和。

第三类是分割转化法，该方法出自17世纪德国数学家开普勒的《测量酒桶体积的新方法》一书。如图3，将扇形AOB的面积对应到△OGH的面积上，虽较为直观，但不够严谨。有的教科书甚至以引理的形式，直接给出扇形面积公式，并没有给出具体的推导过程。

（三）与扇形相关的问题

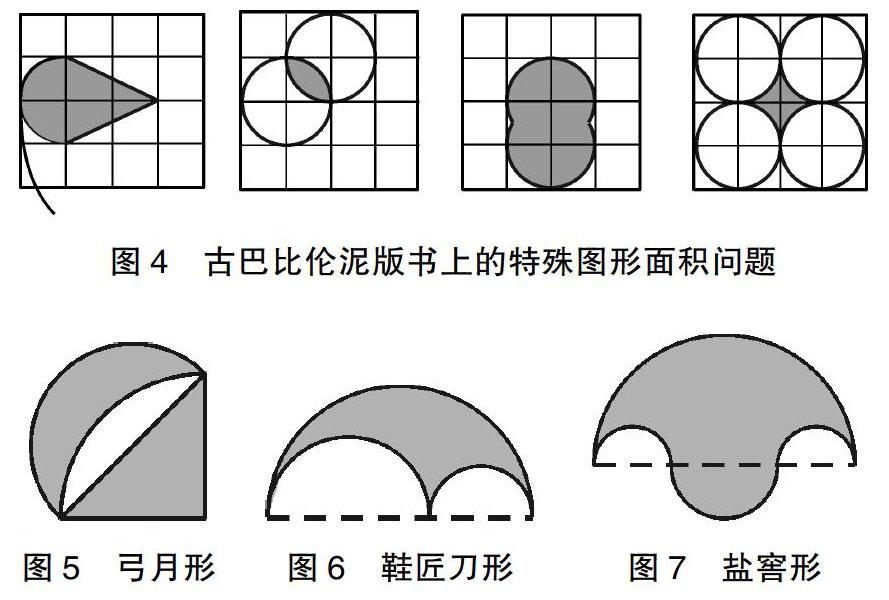
历史上，与扇形面积相关的问题数不胜数。例如古巴比伦时期的泥版书上，记载着一些特殊图形面积计算问题[5-6]，如图4。古希腊数学家希波克拉底（Hippocrates）在研究化圆为方的问题时，发现了与扇形面积密切相关的弓月形。如图5，等腰直角三角形斜边上的半圆与以直角顶点为圆心、直角边为半径的四分之一圆弧所围成的弓月形的面积恰好等于等腰直角三角形的面积。阿基米德（Archimedes）研究过若干半圆所围成的鞋匠刀形和盐窖形等有趣的图形。如图6，大半圆直径上的一点将直径分为两段，而后在每一段上作同侧半圆，那么由三个半圆所围成的图形称为鞋匠刀形。如图7，将大半圆直径分为三段，其中左右两段长度相等，在左右两段分别作与大半圆同侧的半圆，在中间作与大半圆异侧的半圆，那么由这四个半圆所围成的图形称为盐窖形。

16世纪，意大利艺术大师达·芬奇（L.Da Vinci）在他的素描手稿中绘制了很多由圆弧围成的图形（如图8）。其中，图8-a形似银杏叶，由一个半圆和两个四分之一圆弧围成;图8-b形似猫眼，由两个希波克拉底弓月形组成;图8-c由四个蘑菇形组成。

三、两节课的宏观比较

两节课的教学目标基本相同，分别是：（1）认识扇形并理解扇形的概念;（2）掌握扇形面积公式的推导并运用公式进行相关的面积计算;（3）在公式推导过程中体会数形结合、化曲为直和无限逼近等數学思想方法。不同之处在于，教师A通过数学史上的图形，让学生感受数学文化的魅力;教师B则通过数学史上的图形，让学生欣赏几何图形之美。两节课的教学重难点也相似：教学重点为扇形面积公式的应用，教学难点为扇形面积公式的推导。

在教学过程中，教师A和教师B的教学过程均由情境引入、公式探究、公式应用、课堂小结四个环节组成，具体见表1。

由表1可知，尽管教师A和教师B均从HPM的视角实施课堂教学，但两者的教学设计却迥然不同。教师A注重培养学生的探究能力，试图让学生像数学家一样经历扇形面积公式的发现过程;教师B则注重向学生呈现数学家发现和推导扇形面积公式的过程，几乎没有给学生探究的机会;教师A聚焦分割转化法，教师B向学生展示了阿基米德推导扇形面积的方法和分割转化法。总的说来，教师A的设计更符合HPM的教学理念。

四、两节课的微观比较

借鉴本刊往期发表的文章的分析框架[7-8]，我们从四个维度对这两节课进行比较和分析。

（一）史料的适切性

作为HPM工作室的学员，两位教师拥有同样的历史素材，这些素材均来自历史研究，满足科学性。教师A在情境引入环节，呈现了以下材料。

古巴比伦泥版上的特殊图形;

希波克拉底弓月形;

阿基米德的鞋匠刀形和盐窖形;

达·芬奇笔记本中的银杏叶形和猫眼图等。

教师B并未在情境引入环节使用数学史料，而是将上述材料呈现于课前印发的阅读材料中。这些材料有效地激发了学生的学习兴趣和学习动机。

在公式探究环节，教师A借鉴分割转化法设计折纸活动，并在活动之后播放HPM微视频，展示分割转化法;教师B通过几何画板，分别呈现了阿基米德和开普勒推导扇形面积的动态过程。教师A和教师B所用的史料兼具科学性、趣味性、可学性、有效性和人文性。虽然教师B将历史素材呈现得更有趣（学生看到扇形转化成三角形的动态过程，不约而同地发出惊呼），但教师A给学生提供了更多的探究机会。

（二）融入的自然性

要将数学史自然地融入数学教学，需要达成知识的逻辑序、历史序和学生心理序的有机统一。

教师A在情境引入和公式探究环节运用了数学史料。在情境引入环节，教师A在对比学生的绘图和历史上数学家研究的图形的基础上，引入扇形概念;在公式探究环节，教师A借鉴历史，引导学生采用分割转化法发现和推导扇形面积公式。以下是教师A的教学片段。

【教学片段一】

师：历史上一些伟大的数学家也非常喜欢研究用圆弧构造的图形。在大英博物馆所收藏的古巴比伦数学泥版上就发现了由圆弧构造的图案。古希腊著名数学家希波克拉底在研究化圆为方问题时，构造了著名的弓月形，并发现了“月牙定理”。阿基米德喜欢用半圆来研究一些面积问题。到了文艺复兴时期，达·芬奇也喜欢用圆来研究面积问题，比如银杏叶和猫眼图。我发现同学们的作品（如图9）与数学家研究的图形也有异曲同工之妙。

生：是的，我们的作品在很多地方与这些图形有相似之处。

师：老师相信同学们在未来也可以成为小小数学家。请大家观察一下这些图形都有什么共同特征。

生：都是由线段和圆弧所围成的图形。

师：我们把由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。

【教学片段二】

师：扇形面积和组成它的弧长有什么关系呢？下面请同学们以小组为单位，通过动手折扇形来进行探究。

生：将扇形折成若干份，当份数越多时，它会近似为一个三角形。三角形的面积公式为底乘以高除以2，那么扇形面积就是弧长乘以半径除以2。

师：这位同学能想到这一点非常好。其实他的方法与德国数学家开普勒的推导方法是相似的，下面通过一段微视频为同学们介绍他所采用的方法。

教师A展示学生课前完成的作品，并将其与历史上数学家研究的与扇形相关的图形进行对照，让学生发现这些有趣的图形与他们自己所绘制的图形相似。教师A让学生从这些图形中找出规律，于是自然引出扇形定义。由此可见，教师A的引入方式虽未采用从圆到扇形的逻辑序和历史序，但符合学生的心理序。而在探究扇形面积公式时，教师A引导学生采用开普勒的分割转化法，与圆面积公式的推导一脉相承，因而以思想方法为主线，建立扇形和圆之间的联系，基本上达成了逻辑序、历史序、心理序的统一。

教师B在公式探究和公式应用环节运用了数学史料。以下是教师B在公式探究环节的教学片段。

师：大家了解开普勒吗？哪位同学可以说一说？

生：开普勒是德国杰出的天文学家、物理学家、数学家，他发现了行星运动的三大定律，人类在2015年发现了首个围绕着与太阳同类型恒星旋转的且与地球大小相近的行星，其被命名为开普勒-452b。

师：非常好。在学习圆面积公式的时候，我们就采用了开普勒的推导方法，哪位同学能说一下，如何将圆转换成我们熟悉的图形呢？

生：将圆分成若干等份，随着份数的增加，拼成的图形越来越接近直角三角形，一条直角边相当于圆的半径，另一条直角边相当于圆的周长。

师：说得非常好，下面我们一起借助几何画板，用开普勒的分割转化法推导扇形面积公式。

（教师用几何画板展示开普勒推导扇形面积公式的方法，如图10。）

生：将大扇形切分成若干个小扇形，在展开后，把小扇形拼成了一个近似的三角形。

师：最后拼成的近似三角形的底边是什么呢？

生：扇形的弧长。

师：那么接下来我们一起来验证这个公式。

教师B引导学生类比圆面积公式推导扇形面积公式，符合从圆到扇形的逻辑序和历史序。然而，几何画板的动态展示虽然能提高学生的学习兴趣，但在快速演示之下，他们可能并不理解从扇形到三角形的等积变换背后的原理。因此，教师B在兼顾学生心理序方面，还有改进的空间。

（三）方法的多元性

教师A在情境引入环节，呈现历史上数学家研究过的图形，属于复制式。让学生通过动手折纸自主探究，发现规律，经历扇形面积的发现和推导过程，体会其中的极限思想，基本上属于重构式。利用微视频介绍开普勒推导扇形面积公式的方法，属于附加式。

教师B在公式应用环节，展示了数学史上与扇形相关的图形，属于复制式。通过类比圆面积公式的推导过程，展示阿基米德和开普勒推导扇形面积公式的方法，属于复制式。

由于教师A没有设计问题串，因此他对扇形知识的重构并不完善，而教师B完全没有采用重构式。教师A和教师B仅仅呈现古代数学家研究的图形，而没有将有关图形设计成面积问题，因而顺应式是缺失的。

（四）价值的深刻性

悠久的历史、美妙的图形让教师A和教师B的课堂教学散发着数学文化的芬芳。

在教师A的课堂教学中，数学史的教育价值主要体现在探究之乐和德育之效上。教师A借鉴历史设计探究活动，引导学生像数学家一样去研究数学，积累数学活动的经验;同时，通过古今联系，讓学生穿越时空与古代数学家对话，从而亲近数学，增强学习自信心。

在教师B的课堂教学中，数学史的教育价值主要体现在方法之美上。教师B利用现代教育技术，直观地再现数学家的方法，让学生看到数学方法的灵活、多元和神奇。

五、学生反馈

笔者在课前和课后分别对两个班级的学生进行了问卷调查，并对部分学生进行了访谈。在课前的调查问卷中，针对问题“介绍圆面积公式的推导方法”，由于教师B在之前讲圆面积公式时注重数学史的融入，因此她的学生能够写出开普勒推导圆面积公式的方法，这也为学生能够比较自然地接受用开普勒的方法推导扇形面积公式奠定了基础。在教师A所任教的班级中，学生虽然没有明确提及开普勒的方法，但相较于教师B的学生，有更多的学生能够写出具体的类似“化曲为直”的推导过程，这与教师A注重在课堂中渗透数学方法是分不开的。

在课后的调查问卷中，针对问题“在所给的图形中选择正确的扇形”，教师A的学生回答的正确率较高，大多数学生能够选出正确的扇形。教师B的学生回答的正确率低于教师A的学生，错误主要集中在漏选了圆这个特殊的扇形，错选了形如扇面的图形，主要原因在于教师A在课堂练习中讲解了与扇面有关的例题，强调了扇面是由两个扇形面积相减得到的。针对问题“计算给定边长的猫眼变式图中两个弓月形的阴影面积”[DK]（如图11），教师A的学生只有少数人能够正确作答，而在正确作答的学生中，大部分学生利用面积相减的计算方法进行解题，只有极少数学生能看出阴影部分的面积与正方形中两个三角形的面积相等，而教师B的学生答题的正确率则更低一些。显然，这道题目对于六年级的学生在理解和计算上是有一定难度的。

在对部分学生的访谈中，针对问题“对这节课印象最深的内容”，教师A的学生的回答主要是：自己用圆等基本图形画出的作品;自主探究扇形面积公式的过程;开普勒推导扇形面积公式的方法。教师B的学生的回答主要是：用极限思想推导扇形面积公式;借助几何画板展示扇形面积公式的推导过程;古代数学家推导扇形面积公式的方法。总的来说，学生对于数学史是充满好奇的，他们能够接受甚至喜爱数学史融入数学课堂的教学方式。

学生对HPM视角下“扇形的面积”一课的教学评价大致可以分为以下四类。

课堂有意义，经历扇形面积公式的探究过程;

课堂有收获，会利用扇形面积公式进行计算;

课堂有趣味，了解到古代数学家的经历和学术成果;

课堂有反思，感受到数学思想的重要性和奇妙作用。

六、结语

以上分析表明，两节课各有其亮点和特色。总的说来，教师A的教学更能体现HPM教学的特点，而教师B以技术见长，技术为HPM插上了翅膀。教师A和教师B所选择的数学史料都兼具科学性、趣味性、可学性、有效性和人文性，但教师A采用了附加式、复制式和不完善的重构式，而教师B只用了附加式和复制式。教师A在三种序的统一上略胜一筹。教师A借助数学史，在课堂上营造了探究之乐，展示了文化之魅，达成了德育之效;而教师B借助数学史，彰显了方法之美和文化之魅。

通过两节课的比较，我们得到以下启示。

（1）关注基于数学史的问题设计

两节课在数学史的运用方式上并不尽如人意，究其原因，教师根据历史材料编制数学问题的意识还有待加强。没有理想的问题串，就不会有理想的重构。实际上，历史上与扇形相关的图形背后都是求面积问题。

（2）兼顾学生探究与技术运用

教师A的教学长于探究，但在古今联系时，学生并不能直观地看到数学家的方法;教师B的教学长于技术，但学生没有机会亲历探究过程。如果兼顾学生探究与技术运用，那么，数学史的教育价值将得到更充分的体现。

参考文献：

[1]俞宏毓，顾非石.关于“扇形面积”的教学指导研[LL]究报告[J].数学教育学报，2013（2）：44-48.

[2]邹炜华.深入教材，追溯文化，丰富课堂：兼谈“扇形面积”的教学设计与教学反思[J].中学数学教学参考，2017（9）：67-70.

[3]WALKER T.Elements of geometry[M].Boston：Richardson & Lord，1829.

[4]GREENLEAF B.Elements of geometry[M].Boston：Robert S.Davies & Co.，1859.

[5]汪晓勤.从巴比伦祭司到达·芬奇[J].中学数学教学参考，2009（1/2）：131-133.

[6]汪晓勤.数学文化透视[M].上海：上海科技出版社，2013.