p值还是n值：决定显著性差异的结果

2020-08-31文静邵惠

体育科技 2020年2期

文静邵惠

p值还是n值：决定显著性差异的结果

文静邵惠

（杭州师范大学体育与健康学院，浙江杭州 311121）

在假设检验中不论进行均数差异检验，还是率的差异性χ2检验，对于有无差异结果取决于值。文章指出，在样本量确定的情况下，其结果决定于值；但在样本不确定情况下，而决定值大小与样本量有关。在实际应用中，对于表明研究结果是否具有差异时，除了显示值外，同时也要指出研究的样本量。

显著性差异；样本量；概率

1 问题的提出

在实际工作中，抽样研究非常普遍。统计学除了描述统计外，还有推断统计，后者是统计学的精华和使命。统计推断主要有两种方法：一是参数估计，二是假设检验。常见的统计推断方法有独立样本差异性的检验、率的差异性χ2检验，还有配对资料的检验、方差分析等。假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法，作为统计推断的一个重要内容，历来受到人们的极大关注并得到广泛的运用。

2 分析与讨论

在进行假设检验时，检验结果不仅与样本的统计量有关，如样本平均数、标准差，还与样本量有关。在数理统计学计算检验的统计量公式中都有体现，公式中不仅含有平均数、标准差，还有样本量n。如：

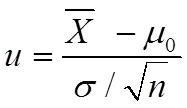
2.1 率的差异性χ2检验案例

率的差异性χ2检验就是比较样本的实际观测值与理论推断值之间的偏离程度。实际观测值与理论推断值之间的偏离程度采用χ2与0比大小表示。例如，2017年10月9日，国庆长假后第一天，某学校对学生出勤情况进行检查，以不同专业的两个班为例，武术与民族传统体育专业班应到学生28人，实到22人；休闲体育专业班应到学生41人，实到35人。问不同专业学生出勤情况是否存在差异，或者说出勤情况与专业有没有关系。根据统计计算卡方值为0.535，值为0.465，表明两个专业出勤率没有差异。然而两个班（样本量）的出勤率明显不等，却推断出两个专业没有差异。而如果类似抽样10次，得到卡方值为5.535，值为0.021，则表明两个专业出勤率存在显著性差异。类似这样的案例在实际工作中会经常遇到，这在统计学中不难解决，可采用列联表分析。

2.2 独立样本t检验案例

表1 不同样本量的统计结果比较表

篮球队员排球队员篮球队员排球队员样本量77 693693 均值64.5765.28 64.5765.28 t值-0.199 -2.137 P值0.846 0.033 结果差异不显著差异显著

独立样本检验用于检验两样本均值所代表的两未知总体均值差异是否具有显著性。例如表1，问篮球队员与排球队员的纵跳成绩有没有显著性差异。可根据独立样本检验来综合判断，而不能简单地回答有还是没有。

2.3 产生不同结果的原因分析

在假设检验中，不同样本量导致结果不一致。从理论上说，产生这些问题的根本原因是抽样误差的存在并且有大小之分，而抽样误差的产生是由于个体间存在差异，并且这种差异是无法改变的。因此，在研究两个样本所属总体是否存在差异时，假设检验应该充分考虑抽样误差的存在及大小。而对同一总体的不同抽样，其抽样误差大小，即标准误是由样本量决定的。一般而言，不同样本的均数一定存在着差异，从理论上讲，当样本量足够大时，它在统计学上会变得显著，即使两样本均数相差0.0001。由此可见，在实际工作中，样本量的确定对判断结果具有决定意义，因此显得非常重要。

样本容量过大，会增加调查工作量，会增加人力、物力、财力、以及时间的成本。而如果样本容量确定的科学合理，一方面，可以在既定的调查费用下，使抽样误差尽可能小，以保证推算的精确度和可靠性；另一方面，可以在既定的精确度和可靠性下，使调查费用尽可能少，保证抽样推断的最大效果。所以在研究具体问题时，得到什么结果是由推算的精确度和可靠性决定的，而这与调查的费用等成本有关。