基于有限元法的双缆水下作业仿真

汤清之 冯正平 黄 维

（1.上海交通大学 船舶海洋与建筑工程学院 上海 200240；2.中国船舶及海洋工程设计研究院 上海200011）

引 言

水下作业被公认为是一个技术密集、学科面广、控制复杂的系统工程，而缆绳的形态仿真更是研究的热点［1］。比较典型的双缆水下作业的工况是当艉甲板在进行长时间的地质取样时，在舷侧或船首可以进行简单的、浅海的水样或生物样采集作业，这样两者由于投掷点距离远且有一根缆缆长较短，故可以同时下水，发生缠绕的可能性也不是很大。即使发生缠绕，也可以舍弃短缆来保护缆长较长的地质缆。当采用双缆同时进行较大深度作业时，双缆之间相互缠绕的风险大增。因此需要对此种工况下的双缆形态进行分析。

本文借鉴了在船体结构中运用比较普遍的有限元法将缆绳进行分段，对每一分段的缆绳采用类似“刚体梁”的办法构建矩阵。然后应用刚体动力学的方法考虑惯性、摩擦、弹性、科里奥利力、重力和外载荷等因素，构造缆绳有限元矩阵的动力学方程。同时在边界条件中引入船舶的横摇、纵摇和垂荡对于缆绳上端点的影响，利用Matlab软件进行方程求解，从而得出缆绳的水下运动状态。

1 船舶运动影响

1.1 水上坐标系

综合考虑全球绝大多数新建的科考船，科考缆绳都是由科考绞车出发，经由滑轮组导向舷侧或船尾的吊架投放到深海中的，这些吊架包括但不限于A型架、L型架、伸缩臂等。当缆绳放入水中一定长度之后，缆绳形成一个柔性的水下系统，而水面上的所有设备和船体形成刚性的水上系统，水上系统和水下系统的分界面为水面，水面和缆绳的交点称为“投掷点”。而且由于船的排水量远大于水下系统的总质量，所以仅仅考虑船舶运动对水下系统的单向影响而忽略水下运动对船舶运动造成的影响。

以右手系法则建立水上坐标系，即船首方向为X正向，左舷方向为Y正向，竖直向上为Z正向，如图1所示。

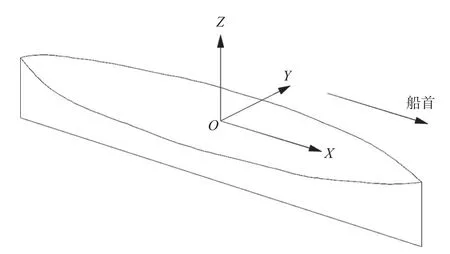
图1 船体水上部分坐标系

1.2 船舶运动

水上运动部分主要考虑船舶的横摇、纵摇、垂荡和在海平面上的漂移，其他自由度的运动由于量级比较小，在本模拟中忽略不计。我们在程序中可以设定一个船舶的摇摆中心O［XO（t），YO（t），ZO（t）］，并在后续的计算中均基于该点进行展开。假设两个投掷点分别为P［X①（t），Y①（t），Z①1000（t）］和P2［X0②（t），Y0②（t），Z0②（t）］，在认为船体及船上的收放设备为绝对刚体的前提下，通过船舶运动可以解出两个投掷点的关于时间t的运动函数。

以横摇为例，一般船舶海上作业时横摇的角度不会超过10°，根据船级社的规范，起重设备的起升索偏移10°对应着6～7级海况［2］，如果超过10°则意味着海况非常恶劣，此时已经超过了A架、绞车的收放设备预留的动载荷系数，将会有造成事故的风险，而且此时人员都难以在甲板上站立，所以我们在此仅考虑小于10°的小角度横摇。由于横摇的角度小、船舶主尺度较大，所以我们认为船舶运动对舷侧投掷点的高度方向位移影响较大，对水平方向的位移影响较小，这也是海工行业波浪补偿吊机优先补偿高度方向的原因，参见图2。

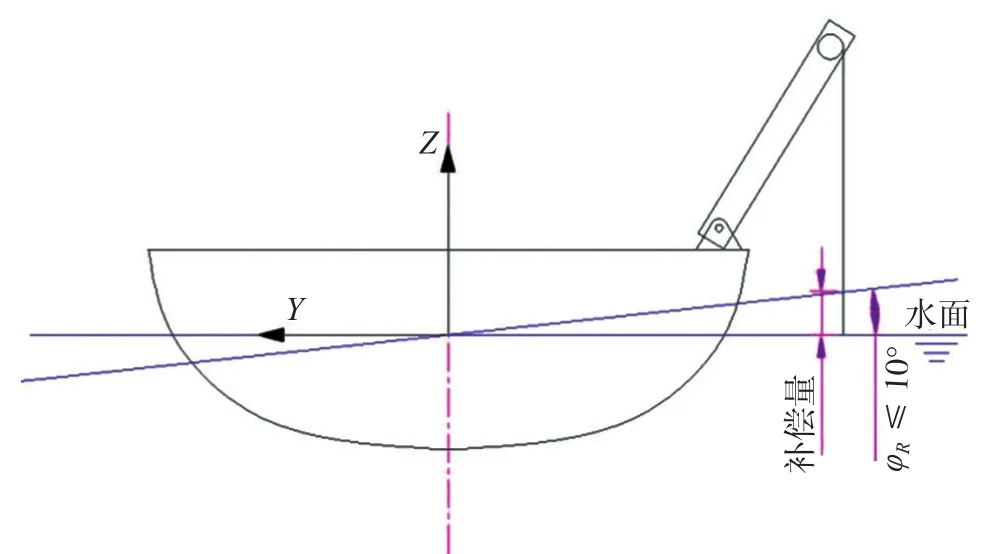
图2 船体横摇运动补偿

实际海上波浪运动是非规则波，但如果考虑复杂的非规则因素会对整个工程模拟造成巨大负担；同时由于科考设备水下作业的时间窗口也就是4 h以内，大多都在1～2 h左右，在短暂的窗口期内波浪情况较规律，船舶对其响应可近似为正弦波。我们可以得到因横摇引起的投掷点高度坐标随时间变化的函数，见式（1）：

同理，因纵摇引起的投掷点高度坐标随时间变化的函数为：

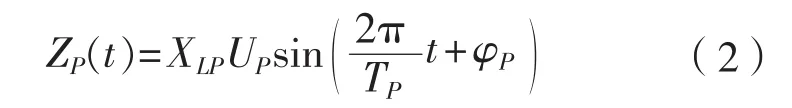
纵摇和艏摇的运动模拟与横摇类似，而垂荡是直线运动，所以需要模拟出垂荡随时间的高度位置变化不必利用几何关系，可以直接认为船舶垂荡的高度变化即缆绳投掷点的高度变化函数，对于规则波，其函数表达式为：

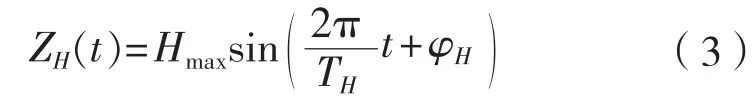
至于水平漂移，很难被界定为一个有规律的函数，但是目前科考船在水下作业时一般都会开启动力定位；此时的水平漂移不会发生剧烈变化，基本上定位精度都能达到20 m以内；对于水下大深度的作业而言这点水平漂移则可忽略不计。

1.3 船舶运动对缆绳系统的载荷

由于船舶运动相当于对水下缆绳系统增加一个额外的载荷，这个载荷在各大船级社规范中都有类似的描述，在中国船级社中称之为“动载力”［2］，而在DNV-GL船级社中称之为“动载荷”，出于习惯本文中也称该载荷为动载荷。由于动载荷的成因比较复杂，而船级社仅是从安全角度考虑预报了动载荷的最大值，并没有给出动载荷随船舶运动的规律，本文假定动载荷的运动规律为：

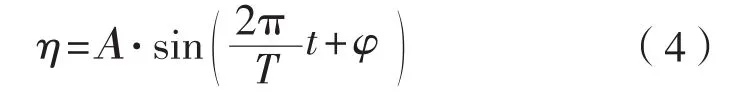
式中：η为动载荷系数；A为波浪运动造成的动载荷系数幅值，对于正弦波形A即船级社规定的起升系数；T为组合后的波浪运动周期，s；φ为波浪运动的相位，rad。

根据式（4），可以将复杂的波浪运动简化为一个正弦函数，然后再用动载荷系数去乘以缆绳在静态时的张力，就可以模拟船舶在波浪中运动带给缆绳的张力变化，加载到整个缆绳系统最上方的端点上。特别是当船舶的运动规律不是在正弦波的情况下，可以用统计学方法将船舶运动回归成其他周期函数，当该周期函数的值域仍是［-1，1］则A值仍可使用船级社规定的起升系数。对于非规则的运动，也可以将动载荷分解为若干个周期函数的叠加。

2 水下缆绳坐标及动力学方程

2.1 水下坐标系

水下系统的仿真主要考虑将连续的缆绳离散化，并将离散化之后的每个分段视作刚形体（即一根梁）。对这些梁而言，其运动应该能满足刚体动力学定理，且其整体也能通过拉格朗日法求其能量的极值。其极值点对应的缆绳形态即为水下缆绳的实际形态。

由于仿真采用有限元法，所以缆绳的水下形态主要通过分段的方式来表达。水下缆绳的坐标系应当分为惯性坐标系（即船体坐标系）和每根缆绳的相对坐标系。每一段对应的相对坐标系与惯性坐标系之间均存在互相转换的关系。假设这条缆绳被分解为n段，则海平面上的点定义为P0（X0，Y0，Z0），而缆绳末端负载的点定义为Pn（Xn，Yn，Zn），每一段缆绳中靠近海平面的一端我们称为始端，靠近海底的一端我们称为末端。始端的坐标为Pk-1（Xk-1，Yk-1，Zk-1）而末端的坐标为Pk（Xk，Yk，Zk），每一段缆绳的末端都可以建立一个相对坐标系∑k：（Ok，Xk，Yk，Zk），该相对坐标系的原点为Ok，而Xk、Yk、Zk分别为其三个坐标轴；其中Yk轴即Pk-1Pk线段在水平面上的投影，而Zk轴始终指向竖直向上方向，Xk轴与Yk轴构成水平面，整个坐标系仍符合笛卡尔坐标系法则，参见下页图3。

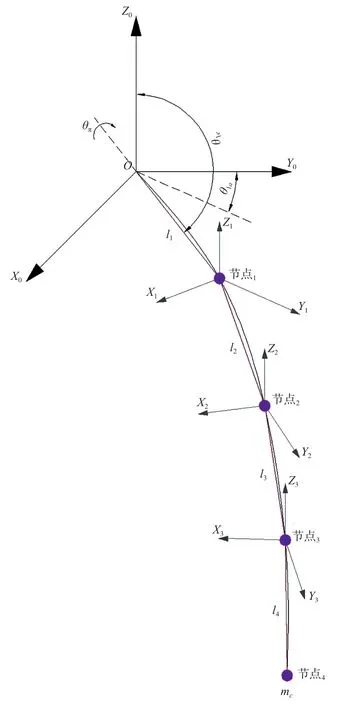
图3 典型4分段缆绳水下坐标系

假设水下缆绳的分段在足够短的长度内近似于直线段，而每一段线段的长度为lk，而第k段线段在其始端所在的水平面内的投影与始端所在的相对坐标系的Yk-1形成夹角θka（该夹角称为方位角）。而第k段线段与Zk-1的夹角为θke（该夹角称为俯仰角）。另外，我们定义缆绳在Pk点相对于Pk-1的自旋角θkT为旋转角。

通过以上阐述，我们可以定义Xk-1Yk-1Zk-1坐标系和Xk Yk Zk之间齐次变换矩阵Hk-1，k，公式如下：

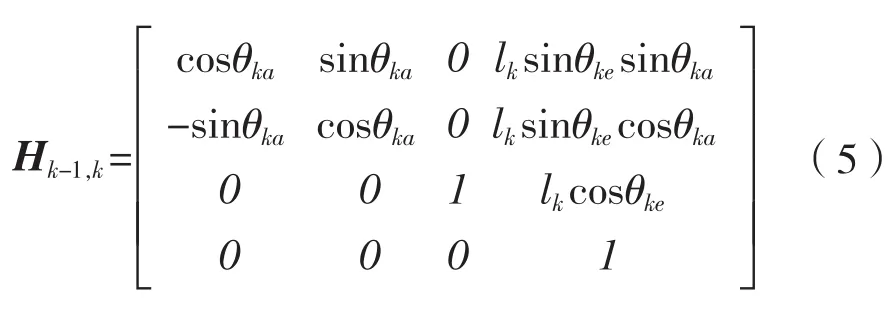
此外，缆绳任意一个节点k的坐标可以表达为式（6）［3］：

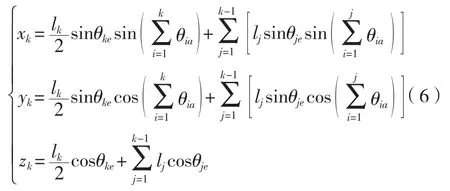
2.2 运动方程

根据刚体动力学方程：

式中：x为刚体的位移量，m；m为刚体质量，kg；c为刚体阻尼，N·s /m；k为刚体的刚度，N/m；F为刚体系统外载荷。

结合2.1节的推导，我们不难得出缆绳基于角度坐标系的运动学方程：

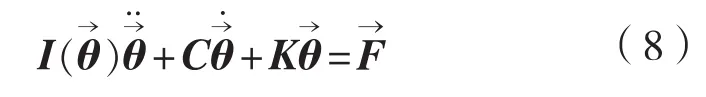
考虑到缆绳系统在大洋深处作业，整个缆绳系统还受到科里奥利力和地球重力的影响，应当将其加入到整个动力学方程中一并考虑。同时缆绳系统的外载荷又可能包括绳端负载物的重力及海流对缆绳的流载荷，如果绳端负载是一个水下机器人的话，其对缆绳的载荷还可能存在各种弯矩，所以这个载荷应该是一个多方向的向量。考虑到这些因素后整个动力学方程可以修改为：

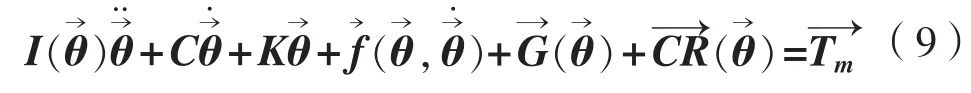
2.3 程序算法

对式（9）进行变换可得：

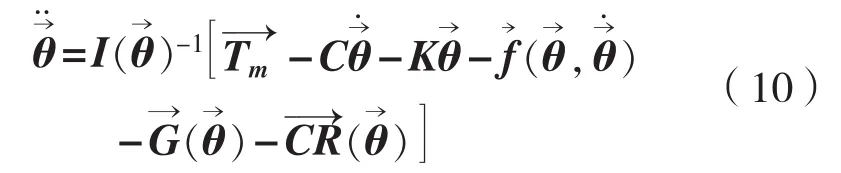
利用Matlab自带的Simulink仿真模块进行两次积分循环就能求解出向量的数值解，再利用式（5）可以将角度坐标转变为直角坐标，然后直接利用Matlab的Plot命令，以时间轴为循环，一帧一帧画出缆绳的水下形态，进而连贯成动画。与此同时，计算某根缆绳所有节点到另一根缆绳所有节点的距离，并求出最小值，作为最危险情况的预报。

根据以上阐述，将对应方程转化为程序语言，该计算程序主要分为数据输入Data模块、微分方程Equation模块、外载荷External_load模块、方程求解的Model_solve模块、坐标处理Position_state_Function模块和最后的结果分析Result模块。这些模块的工作顺序如图4所示。

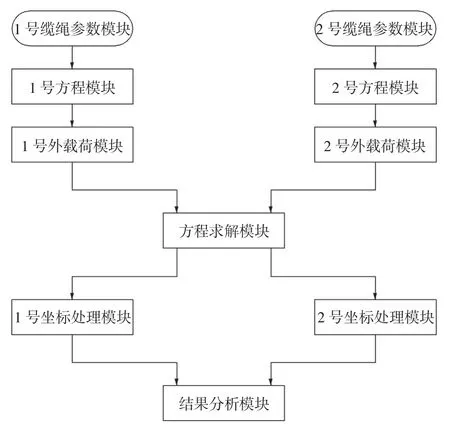
图4 程序流程图

3 算 例

某科考船在南海海域作业，其主尺度为船长100 m、船宽18 m、干舷3 m；配置艉部A架1台、舷侧A架1台。在某海域作业时，利用船尾A架和直径19 mm的钢缆进行地质取样，同时利用舷侧A架和直径17.3 mm的光电缆绞车在舷侧释放1台小型观察级ROV对地质取样的情况进行观察拍摄。根据国内外的一般做法，可在缆绳末端ROV处增加1组力矩来模拟ROV的运动对缆绳的影响［4］。本案例中双缆的初始状态均为竖直向下，ROV在30 s内都对缆绳施加-100 N·m的e方向扭矩和20 N·m的T方向扭矩并在第10 s起对缆绳施加50 N·m的a方向扭矩。现要求仿真30 s时域范围内钢缆和光电缆的水下运动情况，并给出双缆最小距离随时间变化的曲线。

求解过程：首先输入缆绳参数给Data模块，定义舷侧A架处的缆绳为1号缆绳，艉部A架处的缆绳为2号缆绳。缆绳的定位及缆绳参数参见表1。

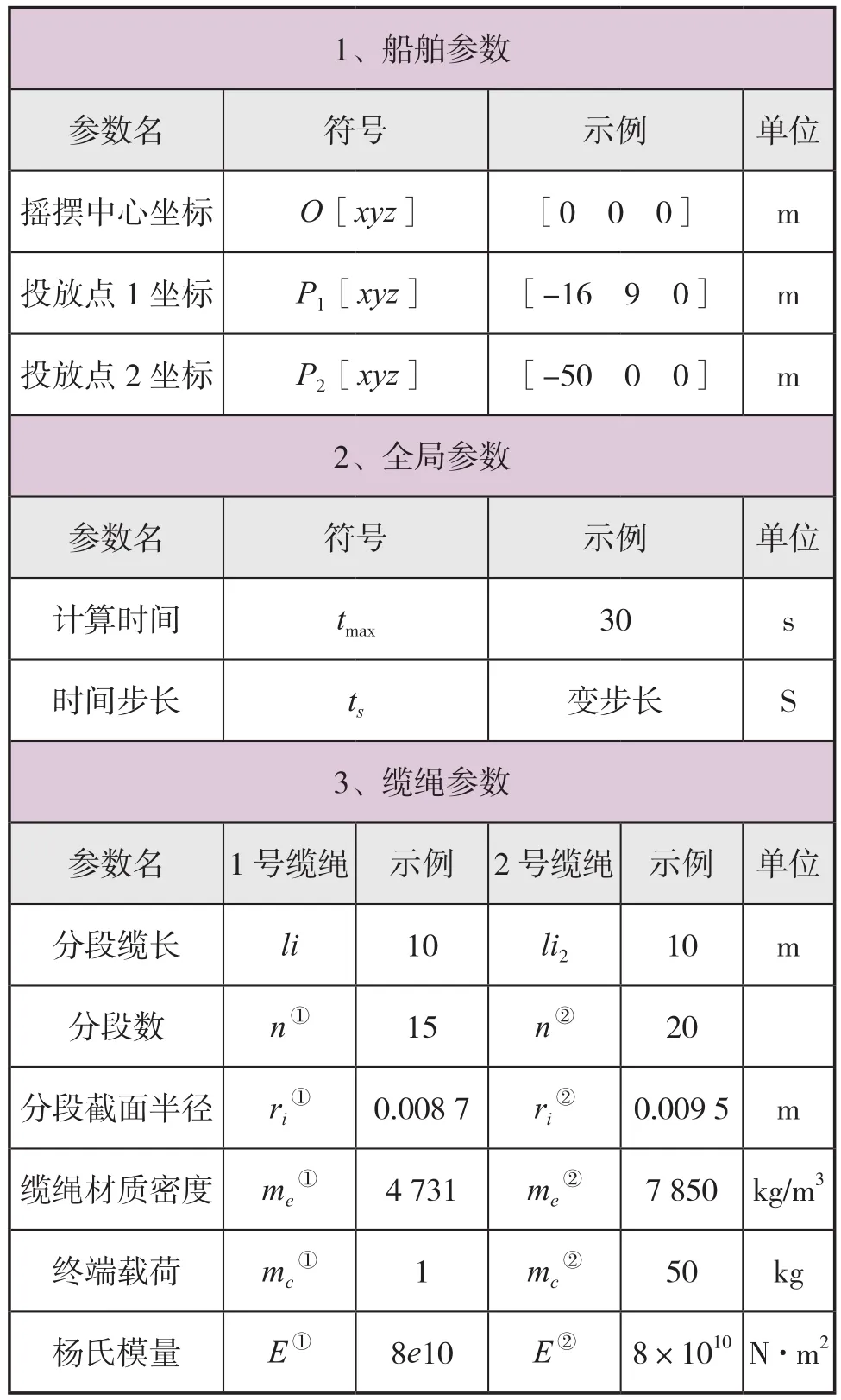
表1 Data模块参数

随后运行model_solve仿真模块，可以求解得到不同时间段θe、θa、θT的数值，将这些数值组成一个三维矩阵，第一维度为节点，第二维度为时间，第三维度为坐标轴，作为整体传输。再利用式6和result模块将角度坐标转换为直角坐标，并利用时间维度将一帧一帧图像中组合成动画。部分仿真动画的截屏如图5～图12，图中沿船长方向的坐标轴即前文提到的X轴，沿船宽方向的即前文提到的Y轴，沿高度方向的即前文提到的Z轴。在运行result的过程中，还可以计算两条缆绳各节点之间的最小距离，并输出最小距离和时间之间的关系曲线。

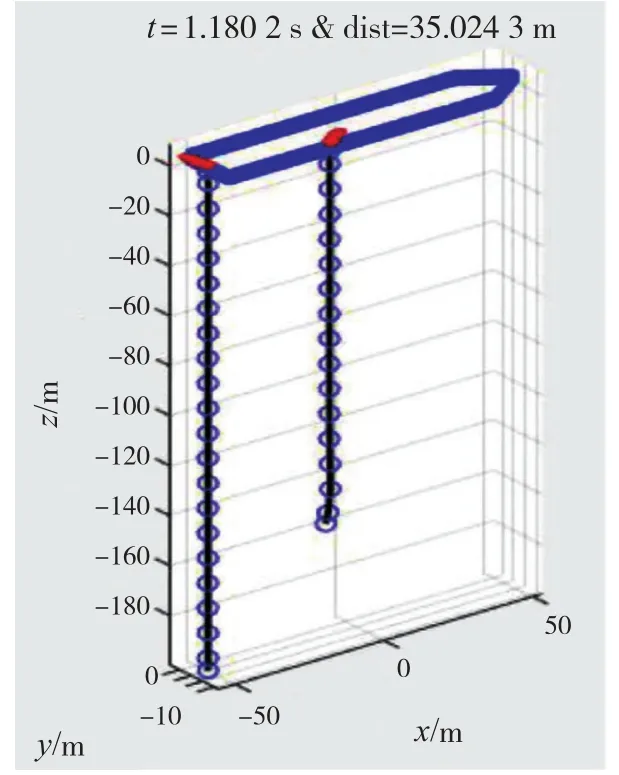
图5 t = 1.18 s时的缆绳水下姿态

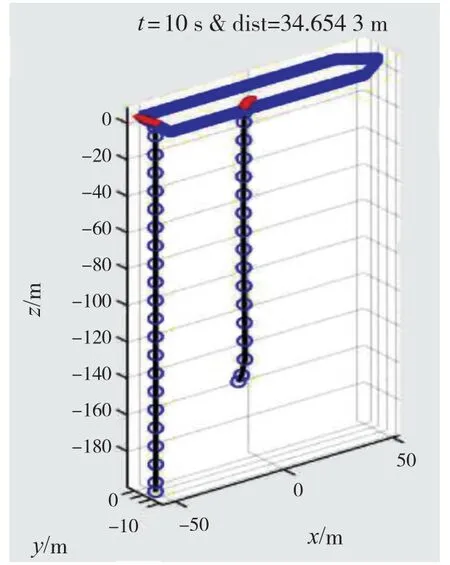
图6 t = 10 s时的缆绳水下姿态

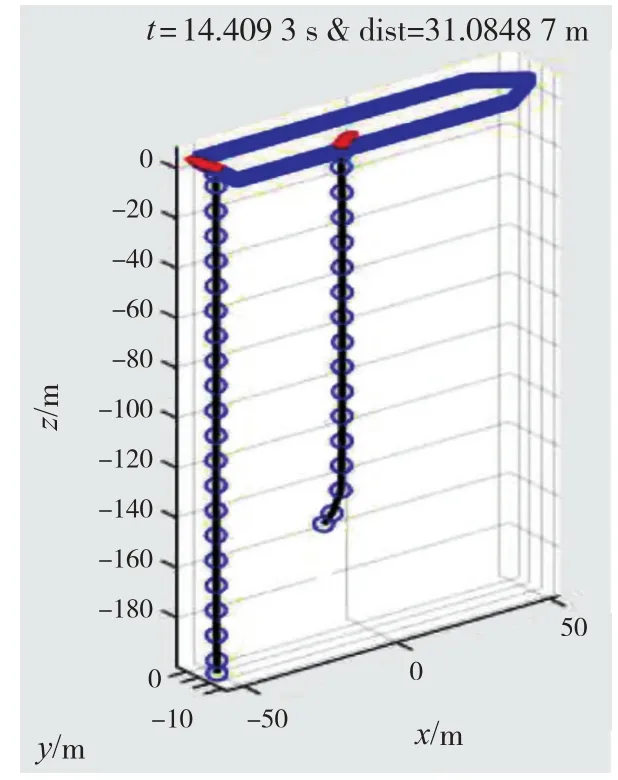
图7 t = 14.4 s时的缆绳水下姿态

图8 t = 17.2 s时的缆绳水下姿态

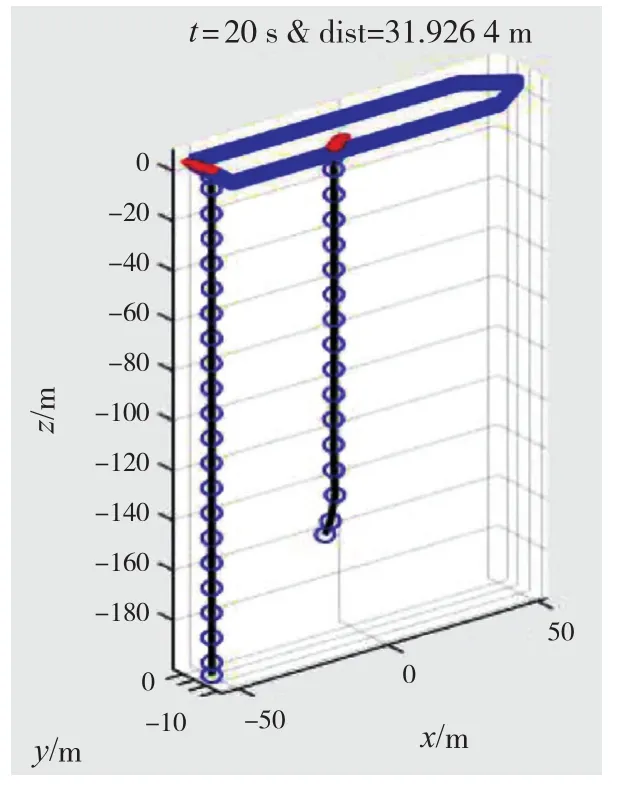
图9 t = 20 s时的缆绳水下姿态

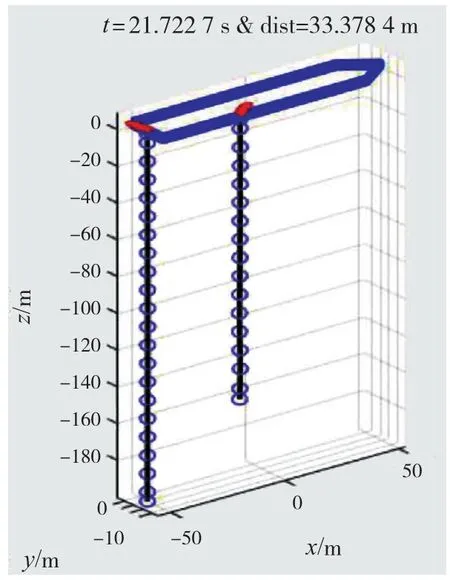
图10 t = 21.7 s时的缆绳水下姿态

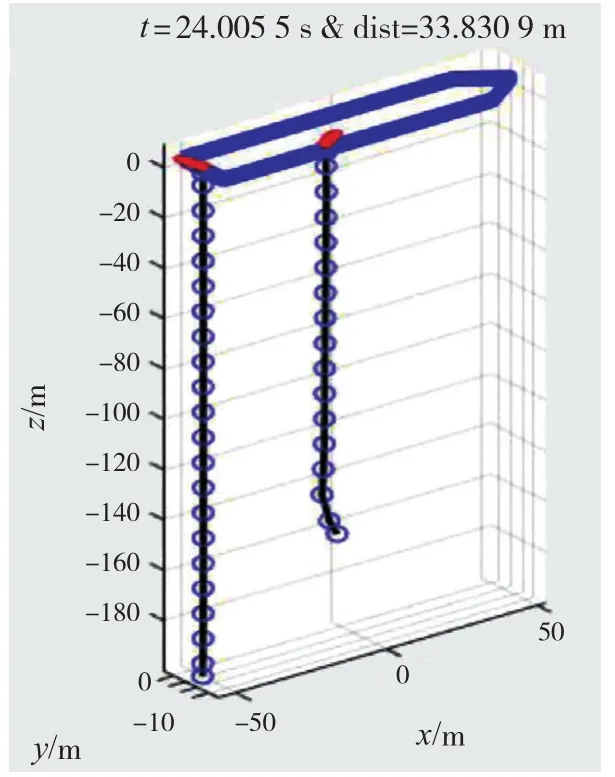
图11 t = 24 s时的缆绳水下姿态

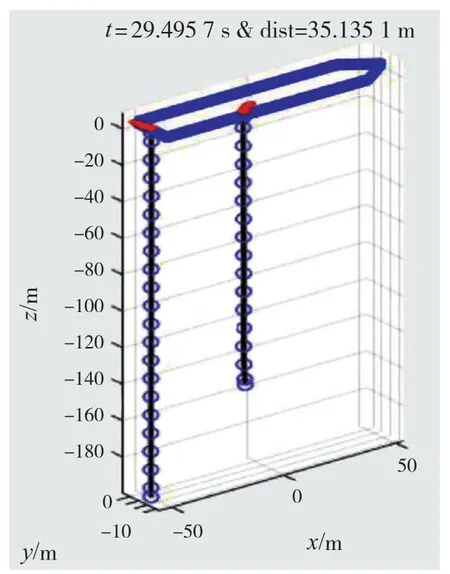
图12 t = 29.5 s时的缆绳水下姿态

根据下页图13缆绳间最小间距曲线看出，本工况下的所有时间范围内的所有最小距离都在30 m以上，最小值为30.269 3 m发生在约17 s时。根据文献，此类工程问题可设定一个最小安全间距，以保证在足够的工程误差下本船的两条缆绳也不会发生干涉［5］。笔者建议，最小安全距离可以定义为最大缆径的100倍，也即1.9 m，目前看30 m的距离远大于1.9 m。所以，经预判上述水下作业的工况是可以进行安全作业的。此外，本文仅是用过在缆绳末端施加力矩的方式来仿真ROV的运动，ROV本身的运动没有绝对的稳态，其在“水下的静止”都是通过水下动力定位来实现的，这部分不属于本文的研究内容，所以本仿真只考虑了30 s内ROV的水下运动。

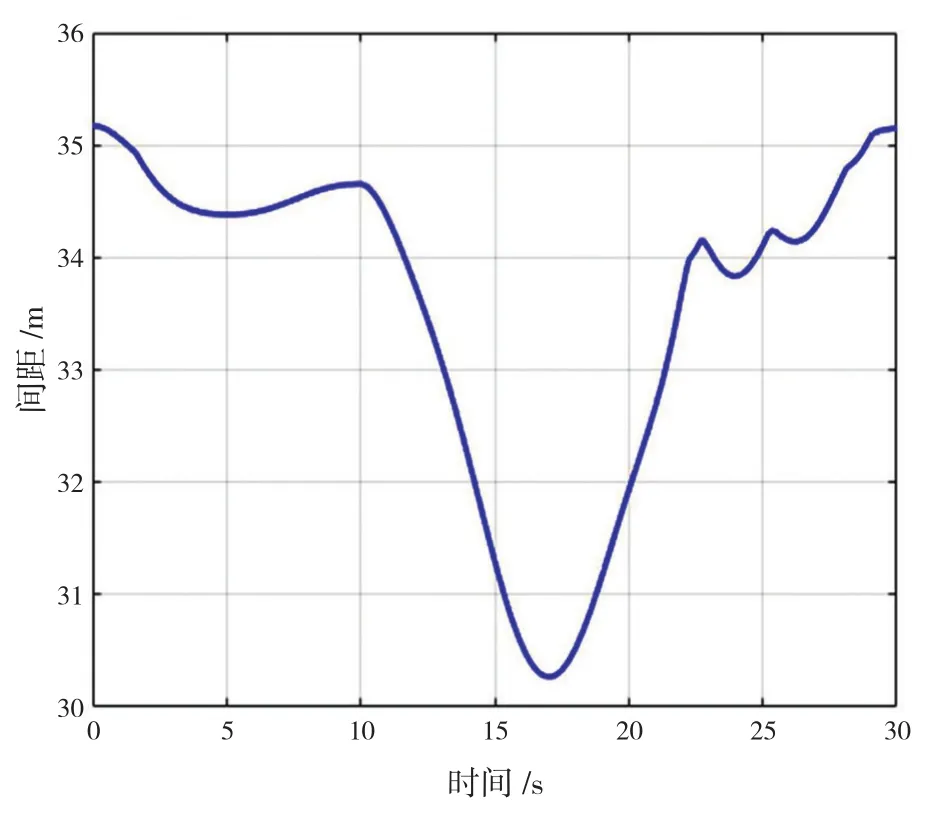
图13 缆绳最小距离与时间的关系

4 结 语

通过上述程序的计算，我们可以有效预判单缆绳和双缆绳在水下的运动形态，进而可以在进行缆绳水下作业之前先测定船舶的运动参数，比如横纵摇的幅值、周期等，再输入缆绳及绳端负载的参数，实现缆绳水下作业的仿真。需要说明的是，实际上，当缆绳释放到一定深度，就会面临缆绳分段数量与计算机能力之间的矛盾，如果缆绳分段过多则会增加计算机负担；而如果缆绳分段过少，则会由于每段缆绳长度过长导致仿真的精度不够。实际上本文仅推荐在短缆作业工况下进行双缆水下作业，在长缆作业工况下，缆绳收放的时间长、缆绳面临的水下流场复杂，难以在计算机中进行数值模拟；所以作业风险非常高，需谨慎对待。这也是本文没有采用长缆作业工况案例的原因。此外，在实际进行双缆水下作业时，往往是海况较为平静的区域，整体的水下情况也比较清晰明了；同时，船长会调整船舶的姿态，使风浪尽可能不影响水下作业。随着动力定位技术的逐步普及，船舶定位的稳定性会越来越强，随着减摇设备的推广，船舶摇摆带来的水下运动影响也会减小，对水下缆绳的安全保障也会越来越高。