螺旋桨叶片自动建模方法
2020-08-28龚京风李瑞洁陈子昊
龚京风, 李瑞洁, 陈子昊, 王 晴
(1.武汉科技大学 汽车与交通工程学院, 湖北 武汉 430065; 2.中国舰船研究设计中心, 湖北 武汉 430064)
0 引 言
螺旋桨在船舶等领域得到广泛应用。不论是在螺旋桨的设计制造阶段,还是在研究水动力、流噪声、空泡特性及优化设计等方面,都需要建立螺旋桨叶片三维模型。然而,传统三维手工建模方法对操作人员使用软件的熟练度有一定要求,且需要投入大量时间和精力,建立模型的准确性受人为因素影响。因此,提出螺旋桨自动建模方法,可有效克服手动建模操作繁琐、工作量大、容易出错等缺点,具有重要的工程实际意义。为了避免传统螺旋桨叶片几何建模方法中手工操作量大的缺点,刘勇杰等[1]提出一种基于CATIA平台的三维建模方法。该方法利用 Excel 表格完成桨叶型值点的计算,采用VB.net语言编写坐标点批量导入程序,读取保存在Excel里的型值点坐标值数据,在CATIA中生成描述螺旋桨叶曲面的型值点。该方法需要在Excel表格中手动操作,对用户操作熟练程度有一定要求,建模工作量仍然较大。吴利红等[2]采用MATLAB语言编制桨叶型值点计算程序,将计算得到的型值点存入标准ProE格式文件,然后在ProE中手动依次导入每一层叶切面型值点,未完成桨叶轮廓线、曲面的自动生成,后续需手动建立桨叶模型且操作步骤繁多。王艳龙等[3]结合螺旋桨二维图绘制方法和CATIA曲面逆向设计方法,运用螺旋桨二维投影轮廓建立螺旋桨三维模型,生成面向CFD的三维模型。该方法需要在AutoCAD根据图谱设计方法得出的型值表中绘制螺旋桨二维图形,且在CATIA软件中的操作较复杂。谢云平等[4]采用船舶设计软件平台NAPA自带的NAPA Basic语言编制宏程序实现桨叶型值点的自动计算。安邦等[5]利用MATLAB软件将螺旋桨的基本参数及不同半径处叶切面二维坐标转换为空间笛卡尔坐标,然后将其导入SolidWorks建立三维几何模型。
为实现螺旋桨叶片自动化建模,依据桨叶二维图制图原理和几何特征推导桨叶型值点计算公式,将计算得到的型值点存入带宏命令的Excel表格,在CATIA中读取该表格,形成桨叶曲面。采用Python语言,将上述流程程序化,形成操作简单、界面简洁的螺旋桨叶片曲面自动建模软件。软件内置智能化提示,为用户正确操作提供指导。
1 建模原理
1.1 型值点的计算
基于螺旋桨设计参数可以得出叶切面型值点的二维坐标。根据不同半径处的弦长、拱度、厚度等轮廓参数,计算得到型值点与导边弦长方向的距离X、叶背型值点与弦长的垂直距离Y1、叶面型值点与弦长的垂直距离Y2。建立坐标系(见图1):以螺旋桨轴线为z轴,指向船尾方向为正;以弦长为y轴,指向随边方向为正;坐标原点位于弦长C的中点。二维桨叶型值点坐标为
式中:y0为叶片型线y坐标;z0背为叶片型线叶背z坐标;z0面为叶片型线叶面z坐标。

图1 二维叶切面示例
依据桨叶二维图制图原理和几何特征推导三维桨叶型值点计算公式[6]。将初始二维螺旋桨型值点沿y轴移动侧斜Cs距离、绕x轴逆时针旋转螺距角β、沿z轴移动纵倾Ra距离,其中侧斜Cs为桨叶投影在垂直于桨轴的平面上时,不对称的投影轮廓桨叶的叶梢与参考线间的距离,纵倾Ra为母线上的点到垂直于轴线且通过母线与轴线交点的平面的距离。最后向相应半径为r的圆柱面投影得到螺旋桨三维型值点坐标:
式中:x背为叶背x轴坐标值;x面为叶面x轴坐标值;y背为叶背y轴坐标值;y面为叶面y轴坐标值;z背为叶背z轴坐标值;z面为叶面z轴坐标值。
1.2 型值点的计算
利用样条曲线依次连接桨叶型值点,生成叶切面轮廓曲线、桨叶随边曲线和桨叶导边曲线。用蒙皮法填充封闭曲线,生成曲面。利用结合命令使得到的曲面组合为一个完整光滑、无缝隙的桨叶曲面模型,最后通过封闭曲面命令得到桨叶几何模型[7-8]。
2 螺旋桨叶片自动建模的实现
采用Python语言调用Excel和CATIA控制建模流程,实现螺旋桨叶建模的自动化,流程如图2所示。

图2 桨叶自动建模流程图
2.1 桨叶型值点自动计算与存储
根据推导的型值点计算公式编写程序语言计算坐标,用循环语句将坐标点按顺序存入带宏命令的Excel表格GSD.xls,计算流程如图3所示。

图3 型值点的计算及存储
对于不同的桨叶,叶切面个数、切面型值点个数不同。通过分析用户提供的二维参数表,自动获取叶切面个数、切面型值点个数,建立的建模软件具有良好的通用性。根据式(2)计算三维型值点,程序代码如下:
xB(i,:)=rcos(((X-0.5C+Cs)cosβ-Y1sinβ)/r);
yB(i,:)=rsin(((X-0.5C+Cs)cosβ-Y1sinβ)/r);
zB(i,:)=(X-0.5C+Cs)sinβ+Y1cosβ+Ra;
xC(i,:)=rcos(((X-0.5C+Cs)cosβ-Y2sinβ)/r);
yC(i,:)=rsin(((X-0.5C+Cs)cosβ-Y2sinβ)/r);
zC(i,:)=(X-0.5C+Cs)sinβ+Y2cosβ+Ra。
计算得到的型值点存入Excel表GSD.xls,程序代码如下:
xlswrite(exportfile,{‘StartCurve’},‘Feuil1’,strcat(‘A’,num2str(k+2)));
xlswrite(exportfile,B_CT,‘Feuil1’,strcat(‘A’,num2str(k+3)));
xlswrite(exportfile,C_CT,‘Feuil1’,strcat(‘A’,num2str(k+3+dian)));
xlswrite(exportfile,{‘EndCurve’},‘Feuil1’,strcat(‘A’,num2str(k+2+2dian)));
GSD表原有宏命令可以实现将点导入到打开的CATIA文件,输入“1”“2”“3”可进行不同形式的导入型值点操作:“1”代表导入点;“2”代表导入点之后按照导入顺序连成线;“3”代表将导入点连成线之后充成曲面。为了降低用户的工作量,修改该宏命令,从而默认建立桨叶曲面。
2.2 桨叶自动建模的实现
采用Python语言编写主程序,实现Excel与CATIA的交互。在Python主程序中启用Excel、CATIA组件,打开Model.CATPart文件和GSD.xls文件,并运行其内部宏命令Main,然后关闭GSD.xls文件。程序代码如下:
import win32com.client
xls=win32com.client.Dispatch(“Excel.Application”)
catia=win32com.client.Dispatch(“Catia.Application”)
catia.visible=1
catia.Documents.Open(catpath)
GSD = xls.Workbooks.Open(gsdpath)
xls.Application.Run(“GSD.xls!Feuil1.Main”)
xls.Workbooks(1).Close()
xls.Application.Quit
catia.Application.Quit
2.3 软件操作界面
软件界面包括操作界面和实时运行提示界面两部分,如图4和图5所示。操作界面可以方便地实现数据的输入与建模结果文件的导出,具体操作步骤如下:
(1) 单击“打开文件”,从弹出的目录框中找到并选择叶片原始数据;
(2) 单击“生成桨叶型值点”,开始计算型值点并将结果储存到GSD表格中;
(3) 单击“另存为”,根据需要将带有型值点数据的GSD表格储存到指定位置;
(4) 单击“桨叶型值点导入CATIA”,可在CATIA中将模型储存到指定位置。

图4 操作界面
实时运行提示界面显示程序当前运行的情况及操作指导,实现软件的友好交互。
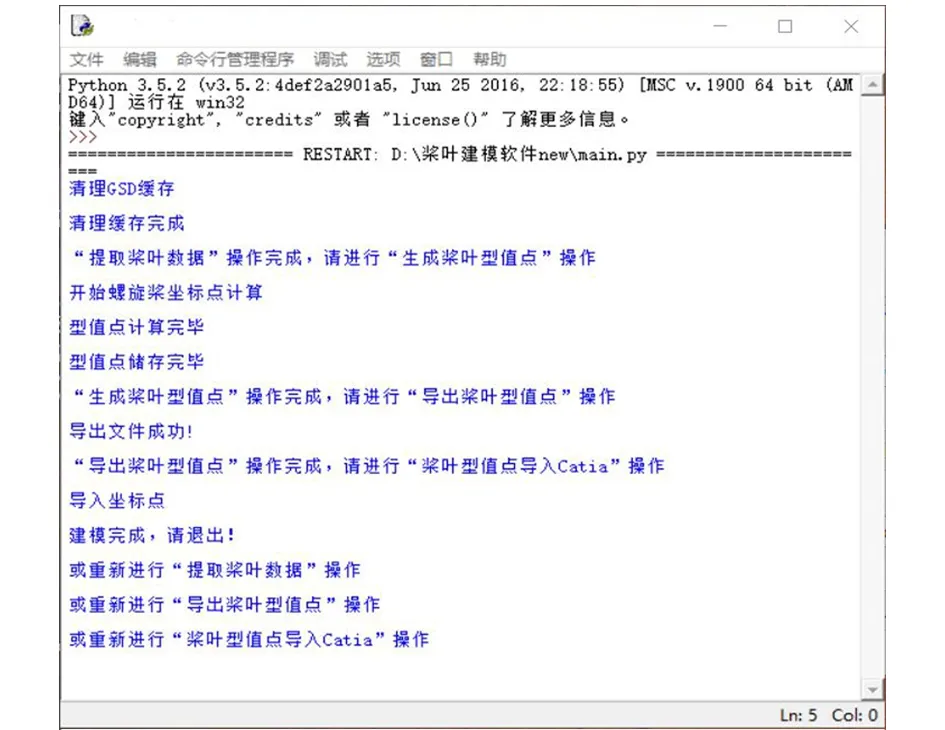
图5 实时运行提示界面
3 自动建模软件的应用
基于波茨坦螺旋桨试验案例(Potsdam Propeller Test Case, PPTC)桨叶二维参数,采用自动建模软件得到如图6所示的桨叶曲面模型。在CATIA中建立的桨叶实体模型与实际PPTC桨叶三维模型一致。所有结果均是在Intel Core I7 CPU,主频为2.5 GHz,内存为8 GB,显卡为NVIDIA GeForce 940MX的计算机上完成,建模耗时约30 s。

图6 PPTC桨叶曲面模型
4 结 论
提出一种利用Python语言,综合Excel、CATIA软件的螺旋桨叶片自动建模方法,可根据不同的螺旋桨参数自动建立具有一定准确性的桨叶曲面模型。基于此自动建模方法,用Python语言编写拥有运算速度快、界面简洁、操作简单等优点的桨叶自动建模软件。建立的桨叶自动建模软件能够有效降低对技术人员的要求,减少工作量,降低人为操作误差,提高准确性,可为螺旋桨设计及性能研究等方面提供技术支撑。
