舵系直接计算法设计
2020-08-28张文斌张光涛
田 野, 张文斌, 王 平, 于 博, 杨 营, 张光涛
(1.渤海船舶重工有限责任公司, 辽宁 葫芦岛 125004;2.渤海船舶职业学院, 辽宁 葫芦岛 125004)
0 引 言
在舵装置的设计过程中,确定舵叶尺寸及布置后需通过计算确定舵系中各部件的尺寸。
在整个舵装置中,舵杆为重要组成部件之一,可将舵机发出的扭矩传递给舵叶。舵干主要受弯曲、扭曲和剪切应力,并且其为运动部件,因此对其受力情况进行准确计算对最终的尺寸选取尤为重要。
目前大型船舶通常采用半平衡悬挂舵,这种型式的舵可以兼顾各部件的强度和设计,易于操作和建造。
现以“渤船”第五代苏伊士油船舵装置设计为基础,对直舵杆型式的半平衡悬挂舵进行计算。
1 直接计算法的使用
目前整个舵系计算的主要依据为规范推荐的经验公式。经过对几个船级社规范推荐的经验公式[1-4]进行研究和对比发现,经验公式的计算过程基本一致,仅在细节要求上有所差别。舵系计算过程如下:
第一步,根据船舶主尺度、最大吃水和航速等信息计算舵叶受力;
第二步,根据舵叶受力计算需要的舵机扭矩,选取舵机容量;
第三步,通过具体的受力分析计算舵销、舵承等部位的受力和弯矩;
第四步,根据第三步的计算结果,计算舵叶板厚度、舵杆/销直径等。
各船级社计算公式在第一、第二和第四步基本一致,只有在第三步有所区别,得到的结果也不尽相同。下舵承处的弯矩MB对最终确定舵杆直径有直接关系,而MB并无准确计算公式。
在查阅较多资料后发现,国内各大设计院在舵系设计时使用专用软件进行受力计算,如DNV的3D-Beam软件等。然而,这些计算软件均为付费软件,且使用这些专业软件需要一定的设计基础。在无此设计条件时,只能按照教材[5]和工程手册中的传统力学分析方法和公式对舵系模型进行分析,推导出实用的简化公式进行直接计算。另外可按照简化公式编写自动计算表格程序,用来快速准确地计算各参数。
2 力学模型简化
按照结构及布置,整个半平衡悬挂舵系可视为带弹性支座的简支梁,挂舵臂对舵系起弹性支撑作用。半平衡悬挂舵受力分析简化模型如图1所示。图1中:h为舵叶形心至下舵承的距离,m;P1为舵叶缺口下部计算均布载荷,N/m;P2为舵叶缺口上部计算均布载荷,N/m;l1为均布载荷P1长度,m;l2为均布载荷P2长度,m;l3为舵叶顶部至下舵承长度,m;l4为下舵承至上舵承长度,m。

图1 半平衡悬挂舵受力分析简化模型
进一步将整个舵系视为3个单独力分别作用在简支梁跨外段上,3个力作用下的C点总位移Y等于3个单独力作用下的位移之和。舵杆的计算模型如图2所示。

图2 舵杆计算模型
3 直接计算法公式
查阅各种设计手册和资料未见可直接用于图2(b)和图2(c)模型的挠曲线方程及转角公式。因此,需进一步将此模型分解,并找到对应的挠曲线方程及转角公式。
分解后的模型与文献[6]中一端固定,B点铰接,在B点外均布载荷的基础模型相近,而该模型有准确的挠曲线方程及转角公式。因此,从该基础模型出发,进行合理的变换,可得到适用于舵系计算的直接计算公式。
一端固定,B点铰接,在B点外均布载荷的基础模型如图3所示。

图3 基础模型
(1) 端截面转角

(1)

(2)

(3)
式(1)~式(3)中:p为模型计算载荷,N/m;a为计算载荷p的长度,m;E为材料弹性模量;I为惯性矩。
(2) 最大挠度


(4)
在X=1+a时:

(5)
可将舵系简化后的模型用2个一端固定、B点铰接、在B点外跨均布载荷梁的基础模型组合得到,如图4所示。

图4 计算模型分解
图2(b)和图2(c)均可进行模型分解,结合舵系布置,可推导出均布载荷q1和q2,以及集中力对舵系C点产生的位移Y为
Y=Y1+Y2+Y3
(6)
(1) 均布载荷q1引起C点的位移Y1计算公式为
(l2+l3+l4)+l1[3(l2+l3)+2l4]}
(7)
(2) 均布载荷q2引起C点的位移Y2计算公式为

(8)
(3) 集中力引起C点的位移Y3计算公式为

(9)
式中:RC为舵杆在C点的支反力。
“渤船”第五代苏伊士油船舵装置计算用数据:P1为均布载荷,取318 640 N/m;P2为均布载荷,取272 820 N/m;E取2.1×1011N/m2;I取(π·D2)/64 mm2;D为计算用舵杆直径,取585 mm;l1取7.2 m;l2取5.0 m;l3取0.4 m;l4取6.775 m。
将对应的计算数据代入式(7)~式(9),可得到:Y1= 0.408 05 m;Y2= 0.603 96 m;Y3= 9.802 2×10-8RC。
C点受力产生的位移Y为
Y=Y1+Y2+Y3=0.408 05 m+
0.603 96 m+9.802 2×10-8RC
(10)
根据模型可得,在C点位置由挂舵臂给予舵叶一个弹性支撑,因此C点支座反力公式为
RC=Y·Kh
(11)
式中:Kh为挂舵臂支撑弹性系数,仅与挂舵臂结构有关,Kh取6.9×108N/m。
联合求解式(10)和式(11)可得RC= 4 745 261 N,Y= 0.006 88 m。
下舵承处舵杆弯矩MB为3个分力对下舵承(B点)计算弯矩之和:MB=P1·l1(l3+l2+l1/2)+P2·l2(l3+l2/2)-RC(l3+l2)= -1 020 650 N·m。
4 复核下舵承处舵杆直径
在计算过程中需先期输入舵杆惯性矩等数据,这就需要在计算时假定舵杆直径,在计算完成后再根据规范要求的公式对假定的舵杆直径进行校核。
下文从应力和规范要求两方面进行校核计算。
4.1 应力校核
文献[3]规定,当使用直接计算法校核舵杆强度时,舵杆的等效应力σe不超过许用应力 [σe],等效应力计算式为
正应力
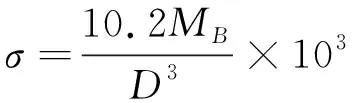
(12)
计算得σ=-52.0 N/mm2。
切应力

(13)
式中:T为舵叶计算扭矩,取2 405 835 N·m。
计算得τ=61.3 N/mm2。
等效应力

(14)
式中:τ为舵杆切应力。通过计算得σe=118.2 N/mm2。
许用应力
[σe]=118KS
(15)
式中:KS为舵杆材料系数。
计算得[σe]=113 N/mm2。
计算结果显示σe> [σe],因此假定的舵杆直径不满足规范要求。
4.2 规范校核舵杆直径
根据CCS规范复核下舵承处舵杆直径[3]:

(16)
式中:Dt为舵柄处传递舵扭矩的舵杆直径。
计算得D=580.4 mm < 585.0 mm (直接计算法假定直径),因此假定的舵杆直径满足规范要求。
4.3 重新迭代计算
根据第4.1节和第4.2节的校核结果,若假定的舵杆直径不满足要求,则需增大计算中假定的舵杆直径重新进行计算,直到满足要求为止。第4.1节计算结果显示,下舵承处舵杆直径选择585.0 mm不满足应力校核要求,因此增大舵杆直径进行重复计算。舵承处舵杆弯矩MB校核等计算结果如表1所示。

表1 校核计算及迭代计算结果汇总
5 结 论
各船级社推荐公式与直接计算法所得结果汇总如表2所示。由表2可知,船级社推荐的公式均非常保守,在实际使用过程中有大量冗余。采用直接计算法可使下舵承处舵杆直径减少10%左右,大幅降低设计成本。
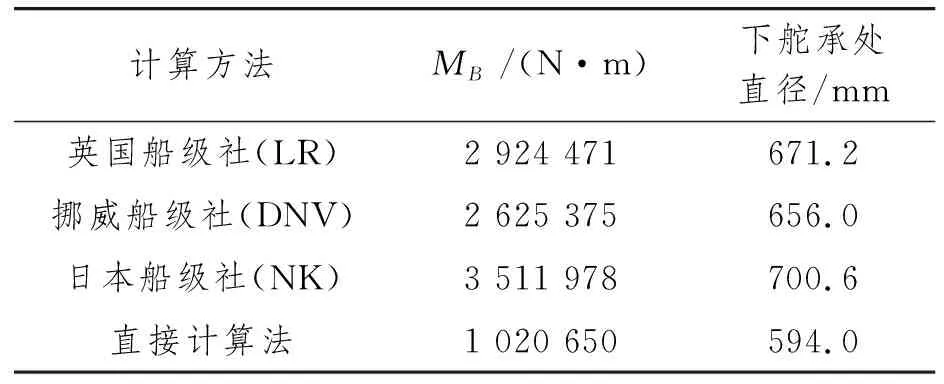
表2 各船级社推荐MB计算公式及直接计算法对比
因此,采用直接计算法进行舵系计算并确定舵杆直径等参数,对新项目的设计和开发具有重要意义,可提高设计效率、降低建造成本,提高船舶的经济性和市场竞争力。
