从图形直观到算式抽象

李小强

作为《义务教育数学课程标准（2011年版）》十大核心概念之一，几何直观是帮助学生描述和分析问题的重要工具。在几何直观中，图形直观又是一个重要分支，在教学中有着广泛的应用，其中，线段图就是最抽象的图形直观，也是最简洁的图形直观。对于三年级学生来讲，他们已经具备了读懂数线图（再抽象一下就是线段图了）的基本经验，能够通过数线图列出算式。然而，在解决实际问题时，学生却很难将画图的方式用于分析问题的过程中，笔者曾对某班三年级学生进行了画图分析问题的调查，有84.3%的学生不明白怎样画图，或不明白如何在图中标注信息。徐斌老师的“画线段图解决问题”更加侧重图形直观到算式抽象之间的过渡与衔接，从“线段图怎么来的”和“怎么画出线段图”两个角度帮助学生更深入地认识和理解线段图，让学生知其然更知其所以然。

【片段一】三问“变与不变”，抽象得到线段图

师：徐老师要考验大家的眼力。如图1，你能发现数学信息吗？

生：有2朵蓝花（图中用白色表示，下同）。

师：如图2，现在谁能用数学语言描述一下？

生：红花（图中用黑色表示，下同）是蓝花的4倍。

师：对，红花的数量是蓝花的4倍。如图3，继续观察，现在什么变了，什么没有变？

生：图形变了，但数量没有变，颜色也没有变。

师：那这个时候红色正方形的数量是蓝色正方形的几倍？

生（齐）：4倍。

师：如图4，现在呢？什么变了，什么没有变？

生：现在有4个红色长方形，有1个蓝色长方形，红色长方形的数量是蓝色长方形的4倍。

师：你说得真完整。

师：如图5，这样呢？红带子的长是蓝带子的几倍？

生（齐）：4倍。

师：认真观察图6，什么变了，什么又没有变？

生：除了带子宽度变了，其他都没有变。

师：也就是说，原来很宽的带子，现在只是变窄了，长度和颜色都没有发生变化。这个时候，红带子的长是蓝带子的几倍呢？

生（齐）：4倍。

师：仔细看图7，它变得更细了。你见过这样的图形吗？它叫什么呀？

生（齐）：线段图。

师：现在，你知道线段图是怎么来的了吧？其实，我们平时生活当中的一些现象或图形，最后都可以变成像这样的线段。今天，我们就来学习画线段图来解决问题。

【赏析】在以往的数学教学过程中，我们往往只重视线段图的工具性，用它分析和解决问题，却极少去思考线段图是怎么来的。所以，学生对于线段图的认识是片面的。本节课，徐老师通过3次图形的变化，让学生对线段图有了更深刻的认识和理解。其中，第一次变化是基本的数学抽象过程，从具体实物（花朵）到数学图形（正方形），即从生活到数学的过程，让学生明白线段图可以解决生活中的问题，而且解决的是一类问题，而不是一个简单的“红花的数量是蓝花的4倍”的問题。第二、三次图形变化分别是从独立的多个正方形拼接成完整的一条带子，再从宽宽的带子压缩为细细的线段图，让学生在“变与不变”之中深刻理解数量关系，抓住数学本质，同时又体会到画图的简洁。

【片段二】三改“问号位置”，深刻理解线段图

师：在生活当中遇到的实际问题，有的没有告诉我们要求什么，有的还需要我们去寻找已知信息。你们能够自己发现问题和提出问题吗？来看这样一个情境（情境图略，图中的数学信息：裤子48元，上衣的价钱是裤子的3倍），你能发现哪些已知的数学信息？

生：裤子的价钱是48元。

生：上衣的价钱是裤子的3倍。

师：这些都是题目告诉我们的，叫作已知条件。根据这两个条件，谁能提出一个数学问题来？

生：上衣要多少元？

师：一件上衣多少元？（记作1号问题）谁能提出不一样的问题？

生：一件上衣和一条裤子一共多少元？

师：一件上衣和一条裤子就可以简称一套，那就是一套衣服多少元？（记作2号问题）谁还能提出一个不一样的问题？

生：一件上衣比一条裤子贵多少元？（记作3号问题）

师：根据条件，我们提出了3个问题，接下来就要解决问题了。这3个问题都很好，不过难易程度不一样，你认为哪个问题最简单？

生（齐）：1号问题。

师：那我们就从1号问题开始吧。徐老师有个要求，今天，我们不是直接解决这个简单问题，而要一起来画线段图。

（画线段图：第一，如图8，教师示范画线段图，提示学生画线段图之前先计划一下，并记得写上裤子和上衣，然后，画出了一条线段代表裤子，标上了数据。第二，如图9，学生在作业纸上画出上衣所对应的线段，一个学生代表在黑板上画图）

师：上衣的价格是裤子的3倍，就要画这样的几段（教师用手比画）？

生（齐）：3段。

师：很好，把已知条件都画出来了。现在，我们需要在图中标出问题。

（学生在作业纸上标注，一个学生代表在黑板上标注“？元”）

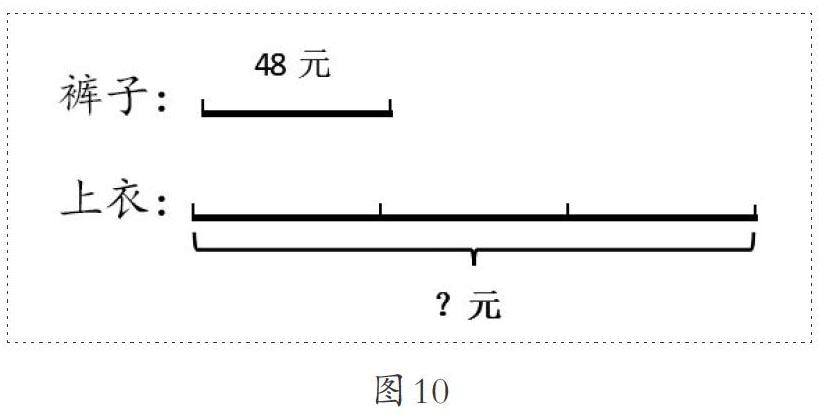
师：这就是线段图。如图10，请大家再看看屏幕上的图和文字，再看看线段图，你看到线段图有什么样的感觉？

生：刚开始看这道题时，理解还有些困难。但当画出线段图后，就可以理解这道题了。

师：请看图10，这是裤子的价钱（48元）。这是上衣的价钱，相当于几条裤子的价钱（3条）。谁能够直接列算式求出上衣要多少钱？

生：3乘以48等于144元。

师：很好，1号问题解决了。我们来看2号问题，这个线段图的问号还能表示一套衣服的钱数吗？

生（齐）：不能。

师：既然不能，请你用橡皮把代表上衣价钱的这个问号擦去，再想一想，一套衣服的价钱应该在线段图上怎么表示？

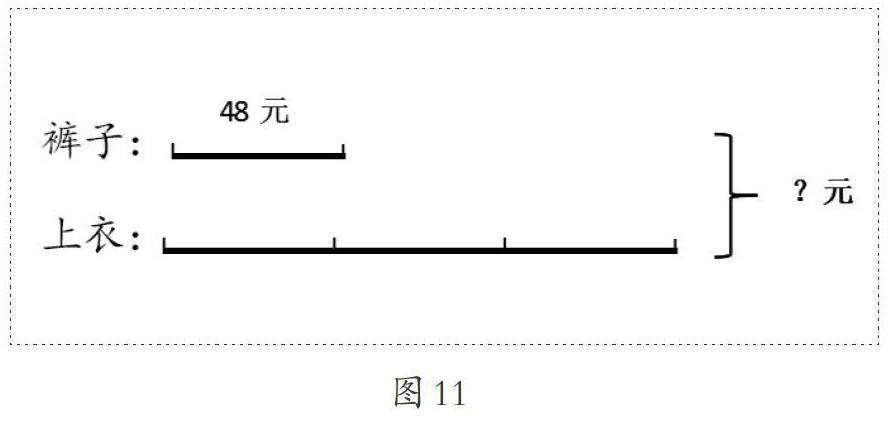
（一个学生代表在黑板上画图，如图11。之后，教师要求其他学生根据黑板上的做法，修改自己的线段图）

师：线段没有变化，现在要表示一套衣服多少元，他在这里标上了问号，对吗？（学生点头示意）请你列算式计算，想想先算什么，再算什么？

（学生在作业纸上自主解答问题，教师选择两个学生代表板书自己的算式）

师：两个同学的结果都是192元，但是算式有点不一样。谁能明白这里的48×3求出的是什么？（教师指着第一种算法）

生：求出的是上衣的价钱。

师：对，就是上衣的价钱，再加上裤子的价钱，就是一套衣服的价钱了。我看到大部分同学是这样算的。再来看看第二种算法，老师有些看不懂了，哪个同学能帮老师解释一下小括号里面的“3+1”是什么意思？

生：上衣有3份，裤子有1份，一套就有4份，每份都是48元，所以用48×（3+1）计算，一共192元。

师：同学们真厉害，不仅会画线段图，而且解决一套衣服要多少钱这个问题时还用了两种不一样的方法。

师：现在我们一起来解决3号问题。首先要自己读题，再用橡皮擦掉表示“一套衣服多少钱”的那个问号，思考怎样表示上衣比裤子贵的钱数，最后在作业纸的空白处列出算式。

（学生在作业纸上自主解答问题，教师请一个学生代表画出表示上衣比裤子贵多少钱的问号，如图12。之后，学生自由表达自己的想法，教师板书算式）

师：谁来说一下自己列出的算式，并解释一下。

生：3×48-48。3乘48表示上衣的价钱，再减去裤子的价钱48元，就求出上衣比裤子贵了多少钱。

师：和他一样做法的同学请举手。有没有谁的方法和他的不一样，也能求出来呢？

生：我列的是48×（3-1）。一件上衣是一条裤子的3倍，用上衣的3倍减去裤子的1倍就是2倍了，再乘以48就是上衣比裤子貴的钱数了。

师：你的思路基本准确，和他的做法一样的同学请举手。

师：刚才，我们一口气提出并解决了3个问题。回顾一下，今天解决问题和以往解决问题好像略有不同，我们是用什么样的解题策略来解决问题的？

生（齐）：画线段图解决问题。

【赏析】发现问题、提出问题、分析问题和解决问题是学生应该具备的4项关键数学能力。首先，思考源于问题，徐老师引导学生在寻找数学信息的过程中发现情境中的已知条件，让学生读懂情境，又鼓励学生从不同的角度提出了3个典型数学问题，这些问题均源于学生对题目的理解，有利于教师更好地读懂学生。

其次，分析问题是解决问题的关键环节，徐老师引导学生利用画线段图分析问题，很好地抓住了题目中的“变与不变”，逐次突破教学重、难点。不变的是已知条件和信息，变化的是所提出的数学问题，如何解决这样的矛盾呢？徐老师巧妙地借助确定问号的位置，为学生建立文字信息与图形直观之间的联系，帮助学生深刻理解线段图，为用好线段图奠定基础。

其中，线段图发挥着重要的作用，比如，在解释“用48×（3+1）求一套衣服多少钱”和“用48×（3-1）求一件上衣比一条裤子贵多少钱”时，线段图的直观与形象，帮助学生清晰地理解“3+1”和“3-1”所表示的意义，一目了然。假设没有线段图，学生很难解释和理解它们表示的意义，更有甚者，可能学生不会想到用这两种算式来解决问题。

在解决问题中，我们需要用图形直观来解决问题，也需要用算式抽象来解决问题，但更重要的是从图形直观到算式抽象的过渡。本节课，一是在变化的图形中发现不变的数量关系，解释线段图的由来;二是在不变的线段图信息中寻找变化的问号在哪里，帮助学生学会画线段图。这样一来，抽象的算式也能形象地解释，有利于学生解决问题。

（作者单位：陕西省西安市长安湖居笔记小学）