基于儿童视角，妙用 数学史教学的策略

李友

德国数学家克莱因提出：“历史呈现了知识的来龙去脉，叙说了人类认识如何步步深入，在抽象的过程中我们就能体会和把握认识提升的关键。”将数学史巧妙地在小学课堂教学中再现，是帮助儿童主动提炼数学信息、探求数学新知、解决数学问题、展现数学思维的一个重要途径。选择符合儿童心理特征和认知规律的数学史进行教学，能激发儿童对数学学习的兴趣，使课堂教学生动、高效，让儿童快速、牢固地完成知识构建，也能让儿童感受到数学的形成与发展的过程，体会到人类通过数学认识自然世界、改变世界的历程。实践证明，数学学习中渗透数学史，会激发学生的数学思考，数学学习将因此变得更有意义、更有内涵、更加丰厚。笔者从以下三个方面阐述在数学课堂中如何运用数学史进行教学。

一、引入历史故事，构建新知网点

数学历史故事精彩而生动，常常能扣人心弦，引发学生共鸣，使人久久回味。在教学中，教师追寻历史长河中某些数学知识产生过程中遇到的人和事，基于儿童年龄特点和个性差异，以“儿童为本”组织教学，从儿童学习数学的认知结构的需求出发，精心选取数学史资料中与学生构建新知相近的故事，巧妙地将相关的数学历史故事引入课堂教学，引领学生在故事中开启思维，拓宽认知边界，把握知识节点，促进数学理解，更好地帮助学生厘清一个个知识产生和发展的脉络，有序编织坚固的知识网。

例如，在教学人教版数学三年级下册“年、月、日”时，根据学生已有的年、月、日生活经验，课前教师让学生思考这两个问题：（1）二月的天数为什么最少？（2）七月和八月为什么连续两个月是大月？教学中，教师利用课件展示古罗马儒略历法的故事，让学生带着问题听故事。

问题1：儒略-恺撒最初是怎样定义大、小月的？全年多少天？（单数的月份定为大月，双数的月份定为小月，全年366天。）

问题2：366天比365天多1天，怎么办？（儒略-恺撒认为，二月处决犯人不吉利，希望二月过得快一点，就在二月份里面减去一天，全年是365天。）

问题3：为什么现在八月是双月也是大月？又采取了什么办法？（古罗马奥古斯特因为自己生日的原因，将八月改为大月，七月和八月就成了连续的两个大月。这样，全年就共有7个大月，4个小月。31×7=217，30×4=120，217+120=337。337+29=366，又多出一天，还是从二月里扣除，这样二月就变成了28天。）

教学中，教师展示儒略历法的故事，学生参与学习的热情得以激发出来，对年、月、日的学习多了一份历史的厚重感，抽象枯燥的年、月、日知识也变得有温情。通过有趣的故事突破新知难点，学生对年、月、日也就加深了理解。

二、借鉴经典操作，掌握新知重点

剪切、拼写、折叠等手脑并用的过程是一个再创造的过程，是以实际问题为出发点，经过系列的操作、分析、提炼，抽象出一般的数学原理、原则及方法，从而实现解决同类问题的过程。根据儿童的天性与成长规律，学生要想将课堂所学的知识内化成自己的知识，形成自己的见解，提高学习能力，必须自己动手操作，手脑并用。数学史料中记载着许多经典的学习操作法。在教学中，基于儿童动作思维的认知特点，教师要不露痕迹地把历史经典操作场景带到学生面前，唤醒儿童的活动经验，引导学生跟着经典进行表象操作，思考这种经典操作法与自己方法的异同，由此理解数学原理，掌握知识重点，增强思维的灵活度。

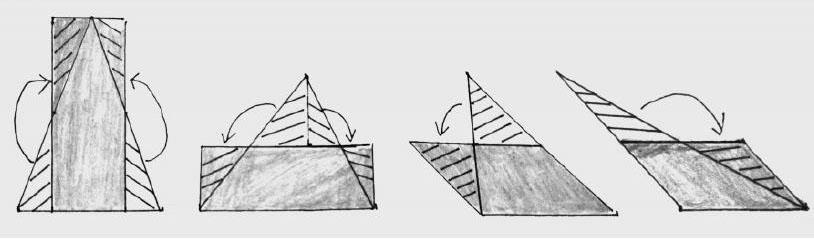
例如，在教学人教版数学五年级上册“三角形的面积”时，学生依据教材提示，将两个完全相同的三角形拼成平行四边形，通过寻找拼成的平行四边形与三角形的各部分关系，初步推导得出三角形面积的计算公式。这时，教师利用多媒体介绍《九章算术》中记录的“出入相补”数学原理，鼓励学生跟着史料介绍的“多余补不足”的操作法，进行分组操作研究（如下图），边操作边记录，再分层口述操作的发现。

学生在从实物操作到借鉴经典进行操作的活动环节中，轻松寻找出计算平面图形的面积规律，个性思维得以充分展示，认知结构得以完善，明白了“出入相补”原理与转化思想运用有着本质上的联系。三角形转化成平行四边形（或长方形）后，两者之间的等量关系是推导平面图形面积计算公式的“根本”，而懂得为什么要沿着高或高的一半或腰的一半剪拼，为什么要转化成平行四边形（或长方形），则是推导三角形面积计算公式的“灵魂”，“根本”是显性的，“灵魂”是隐性的。学生会慢慢地淡忘数学知识，但是数学活动经验、数学方法思想却能帮助学生理解掌握新知重点，提升数学核心素养，让学生终身受用。

三、再现数学名题，突破新知难点

数学名题是古人用数学知识去解决问题的智慧结晶。正如数学家波利亚所言：“只有理解人类如何获得某些事实或概念的知识，我们才能对人类的孩子应该如何获得这样的知识做出更好的判断。”人教版数学教科书常以介绍什么人、什么时候创造的数学成就来呈现数学史实。在教学中，教师要充分考虑儿童的身心发展规律、经验、情感等，结合儿童的思维特点，通过设计合理的教学环节，再现数学名题，帮助儿童找准解决数学问题所需的各个知识点的联系与区别，引导儿童学会面对新知联想旧知，从一种方法迁移到另一种方法。数学名题的筛选和使用，会让儿童将所学的知识与方法前后贯通，真正理解各种知识与方法之间严谨的逻辑关系，进而突破知识难点，降低学习难度，提高课堂教学效率。

例如，在教学人教版数学四年级下册“鸡兔同笼”问题时，教师在学生学会用画图法、列表法、假设法解决简单的“鸡兔同笼”问题后，适时引入古代《孙子算经》中的“鸡兔同笼”原题，学生积极参与古人解题方法的探究过程，猜想得出：（1）先假设让鸡抬起1只脚，兔子抬起2只脚，还有94÷2=47（只）脚。这时地上的兔子脚数比鸡脚数多1，脚与头的总数之差为47-35=12，兔子的只数就是12。（2）假设鸡与兔子同時抬起2只脚，这时还剩下94-35×2=24（只）脚，鸡屁股着地，只有兔子的2只脚在地上，有24÷2=12（只）兔子，有35-12=23（只）鸡。（3）假设让兔子抬起2只脚，35×2=70（只）脚，脚数和原来差94-70=24（只）脚，这24只脚正是每只兔子抬起的2只脚的总和，有24÷2=12（只）兔子，有35-12=23（只）鸡。以上三种形式的“抬脚法”不必要求学生一一猜想得出，只需引导学生观察对比《孙子算经》中讲解的“抬脚法”与自己掌握的三种方法之间的联系与区别。通过比较、思考、沟通，学生发现画图法和列表法实际上就是假设法的基础，“抬脚法”其实也是假设法，都要通过假设、计算、推理、调整，最后得出结论，实际上都是蕴含假设的思想方法，只要找准鸡的只数、兔子的只数与脚数的变化规律，变抽象为直观，就能形成牢固的认知结构。数学名题的再现激发了学生学习兴趣，学生被数学名题蕴含的逻辑性所吸引，学生充分展开联想，寻找联结点，把握知识的来龙去脉，不但难点得以突破，数学知识也学得更深厚。

数学史对儿童的教育价值是多方面的，在数学教学中，教师要基于儿童视角，以儿童为中心，在教学实践中注意积累，用心关注，用心研究，巧妙选择，有效渗透数学史。在数学史文化的滋养下，学生能增长知识，发展技能，升华情感，活跃思维，学会更加理性地对待数学问题，逐步提升数学核心素养。

（作者单位：福建省莆田市涵江区国欢中心小学）

本文系教育部福建师范大学基础教育课程研究中心2019年开放课题“基于儿童立场的小学数学课堂教学策略的研究”（课题批准号KCX-2019061）阶段性研究成果。