考虑尾流效应的双馈风力发电机组并网频率控制策略

栾祥霖，谢冬梅

（沈阳工程学院a.研究生部；b.电力学院，辽宁沈阳 110136）

1 考虑尾流效应的风电场建模

1.1 Jensen尾流模型

风电场尾流模型大致可以分为3 类：基于涡流理论的模型、基于N-S 方程的CFD 模型和基于实验总结的半经验模型。其中，最为经典的半经验模型为Jensen 尾流模型，如图1 所示。Jensen 尾流模型适用于地势平坦的风电场尾流计算，其原理简单，运算速度快，尾流的影响区域随着距离增大而扩大，在风机后为圆锥形区域且均匀分布。

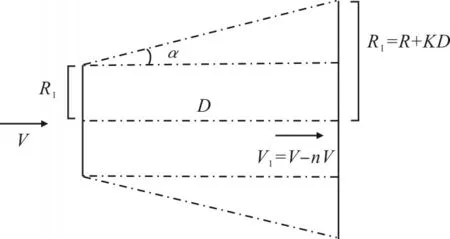
图1 Jensen尾流模型

气流流过半径为R的风机叶片，速度为V，则距离风机风轮下游某点，轴向距离为D处的尾流风速V1可表示为

式中，n为尾流系数：

随着距离D的增大，后排风机受到尾流效应的影响将会减弱，尾流风速V1将会减小。R1为尾流半径；CT是推力系数，其值与风力发电机桨距角β和接收到的风速V有关；K为尾流衰减系数。

综上所述，当前一排风机接收到的风速为V时，后一排风机接收到的风速可以由式（1）计算得出。所以，在风电场内只需要测出第一排风机的风速，其余风机捕获到的风速便都可以计算得出。

1.2 风电场多机等值

图2 为风电场受风示意图。当气流流过左侧第一排风机时，由于尾流效应的影响，后面的5 排风机捕获到的风速要小于前一排。因此，风机捕获到的风速会呈现递减的趋势。结合Jensen 尾流模型，每一排风机的风速都可以通过计算得出。

图2 风电场受风

2 功率备用控制原理

双馈风力发电机在低风速下最大功率跟踪控制，不参与电力系统的频率调整；在高风速时，采用减载控制策略。当电力系统频率发生波动时，双馈风力发电机通过改变转速或者改变桨距角，发出备用功率对系统频率进行支撑。

2.1 变桨距减载控制

风能利用系数Cp是一个与桨距角β和叶尖速比λ有关的函数，如式（5）所示。增大桨距角β，风能利用系数Cp会降低。

图3 是在同一风速、不同桨距角的条件下，双馈风力发电机的风能利用系数和叶尖速比的关系曲线，图中β1＞β2＞β3＞β4。可见，增大桨距角会使风能利用系数降低。

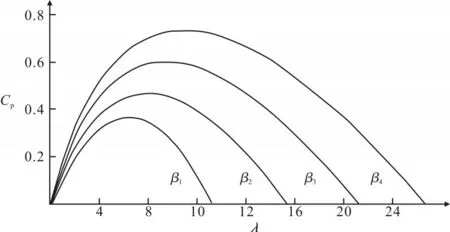
图3 风能利用系数与桨距角和叶尖速比的关系

当风速为V时，通过风力发电机桨叶气流的动能为Pw，如式（6）所示。

式中，ρ为气流密度；S为风力发电机的受风面积。但是，气流通过风力发电机桨叶时，其动能并不能被风力发电机完全吸收。因此，风力发电机输出的机械功率Pm的表达式如式（7）所示。

由式（7）可知，Cp的减小将使风力发电机输出的机械功率Pm减小。

由式（5）和式（7）可知，高风速时，增大双馈风力发电机的桨距角，可以减小有功功率输出，使得风力发电机保留一定的有功功率。

2.2 超速减载控制

图4 为同风速下双馈风力发电机功率-转速特性曲线，AC 为最大功率跟踪曲线，BD 为超速减载曲线。若风速为V3，风机沿最大功率跟踪曲线运行，转速为ω1，其输出功率最大。此时，增加转速或者减小转速都可以使风力发电机有功输出降低，但是减小转速容易使风力发电机受到干扰，影响其稳定性。所以，通常情况下增大转速，使MPPT 曲线右移，以此来实行超速减载控制。

图4 风机输出功率与转速关系

3 双馈风力发电机调频控制

3.1 超速与桨距角协同频率控制

图5 为双馈风力发电机参与电力系统一次调频曲线。发电机的减载程度为d，输出功率Pm的表达式如式（8）所示。依据风速的不同将风力发电机分为3 个运行区间，在各区间内使用不同方法对风力发电机进行减载控制。

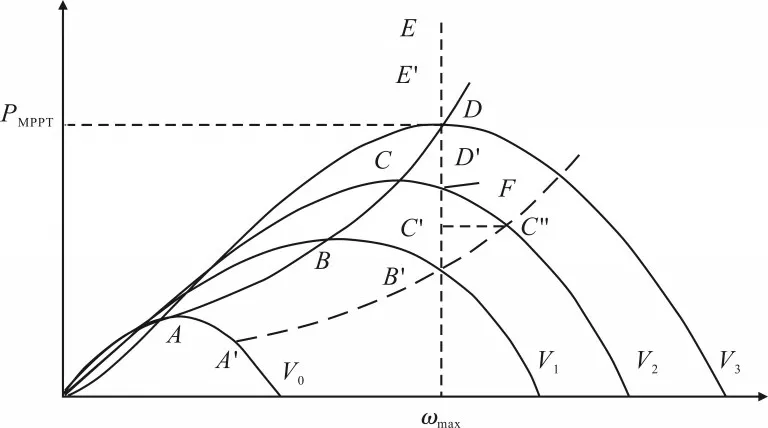
图5 频率控制原理

3.1.1 区间一控制模式

风速区间一为(V0,V1)。其中，V0为切入风速，低于切入风速时，风机转速较小，不参与并网。在区间一内，风力发电机只采用超速减载控制，桨距角始终保持在0°，A'B'为减载程度为d时的运行曲线。

3.1.2 区间二控制模式

风速区间二为(V1,V2)。风速为V1，AB 减载程度为d时，风力发电机在B'点运行，此时风机达到最大转速ωmax。若风速继续增加，仅凭借超速减载控制无法达到减载程度为d的要求。此时，应增大桨距角来弥补剩余的减载量。V1′处于区间二的某一风速，若此时只采用超速控制，风力发电机本应在C''点运行，但受到最大转速的限制，先使用超速控制达到F点，再通过变桨距控制使风机在C'点运行。

3.1.3 区间三控制模式

风速区间三为(V2,V3)。其中，V3为切出风速。当风速到达V2时，转速达到最大，不能继续增加，所以此区间内只能通过变桨距控制实行减载。当减载程度为d，风速为V2时，对应的运行点为D'点；风速为V3时，对应的运行点为E'点。

3.2 计及尾流效应的频率控制器

计及尾流效应的频率控制原理如图6 所示。尾流模型模块通过当前的风速V计算出各排风力发电机接收到的风速，频率控制器通过对应的风速区间来决定运行方式。同排风机受到尾流效应的影响相同，所以运行状态相同。

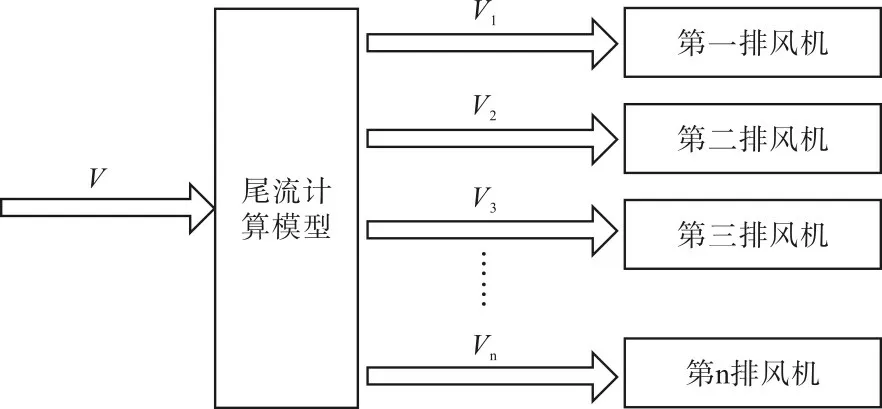
图6 计及尾流效应的频率控制原理

风力发电机的频率控制器如图7 所示。输入量为风速V、减载程度d、系统频率f和风力发电机的实际转速ω。风速区间判定模块判定风力发电机接收到的风速属于哪个区间，结合减载程度d对风力发电机执行相应的频率控制。

图7 频率控制器

当系统频率发生变化时，频率响应模块模拟常规同步发电机的功-频特性，频率降低时增加有功出力，频率升高时减少有功出力。转速控制量Δω通过比例微分控制器结合频率相应模块的有功功率控制量ΔP对风力发电机转速进行调节。

风力发电机的最高转速为ωmax，切入风速为V0，临界风速为V1，切出风速为V3（由风力发电机制造商提供），可参加超速控制的最高风速V2为

式中，n为变速比；λopt为最优叶尖速比；R为风力发电机叶片半径。

假设风力发电机参与调频时在图5 中曲线BB'上的某一点运行，此时风力发电机的输出功率P2如式（10）所示。

式中，PB′为风力发电机在B'点的有功功率；ΔP为风力发电机输出的有功增量，如式（11）所示。

式中，f为电力系统实际频率；f1为电力系统额定频率；k为频率响应模块中功-频曲线的斜率。此时，风力发电机的减载水平将会减小，由原来的d变为d′，如式（12）所示。

此时，可通过减载程度为d′的曲线求出参考转速ωref。在风速区间二中，超速控制和桨距角控制协同作用，ωref表达式如式（13）所示。

式中，ωMPPT为风力发电机在最大功率跟踪方式下的最优转速，可通过式（14）求取。

转速控制模块根据风速和减载程度计算参考转速ωref，再与实际转速比较，得到转速控制量Δω。

桨距角控制环节如图8 所示。转速控制量Δω经过比例微分控制器和一阶惯性环节，得到一个桨距角参考值βref，并作为变桨距机构的输入，βref的表达式如式（15）所示。

变桨距机构近似为1 个一阶惯性环节，并根据变桨距机构的实际能力对β进行限幅操作，得到桨距角的控制量β，β的表达式如式（16）所示。

式中，T1为一阶惯性环节的时间常数。

图8 桨距角控制

4 仿真分析

含双馈风力发电机组的电力系统接线方式如图9 所示。系统初始频率为50 Hz，同步发电机额定容量为10 MW，t=5 s时的突增负荷为0.5 MW。

双馈风力发电机的频率控制器在Matlab/Simulink 中的仿真模型如图10 所示。设定风机额定容量为2 MW；定子电阻R1为0.062 Ω；定子漏抗X1为0.051 8 Ω；励磁并联支路电阻Rm为134.802 Ω；励磁并联支路电抗Xm为4.223 Ω；减载程度d为10%；切入风速为4 m/s；切出风速为25 m/s；最大转速为1 800 r/min。

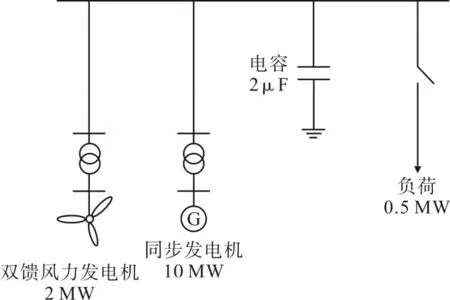
图9 电力系统接线方式

以5 行5 列的风电场为例，风机的风轮半径为35 m，轮毂高度为80 m，各排风机相距400 m。针对风电场各风速区间内的典型风速的尾流模型和频率控制器进行仿真，得到各排风机计及尾流效应影响后实际接收到的风速，如图11所示。

由图11 可知，由于尾流效应的影响，各排风力发电机所接收到的风速呈递减趋势。

图10 双馈风力发电机频率控制器仿真模型

图11 各排风机接收到的风速

以9 m/s 风速为例，对风力发电机频率控制器进行仿真，结果如图12所示。

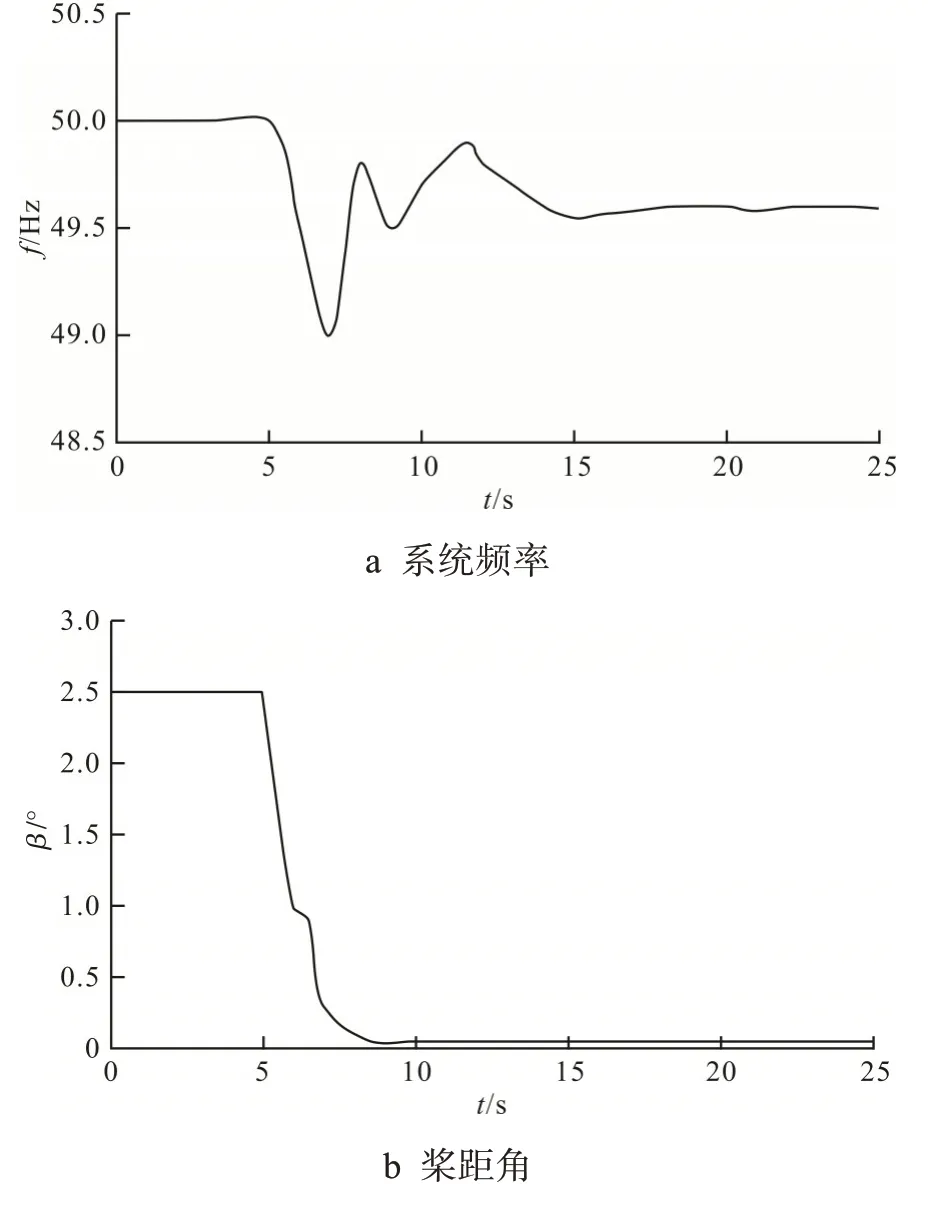
图12 9 m/s风速的仿真曲线

由仿真结果可知，风速为9 m/s时，超速控制与变桨距控制协同作用。当负荷突增时，转子的转速变慢，桨距角减小，释放备用功率对系统频率起到支撑作用，提升了系统频率稳定性。

5 结语

由于尾流效应的影响，风力发电机可能运行于不同的状态，所以参与电力系统调频的能力也各不相同。考虑风电场尾流效应的影响，对双馈风力发电机组进行多机等值建模，采用超速减载控制和变桨距减载控制的综合控制方法，在不同风速下对风力发电机采取不同的控制策略。仿真结果表明：考虑尾流效应的频率控制器能够很快地响应系统频率变化，对系统频率有良好的支撑能力。