农业机器人并联视觉云台研究

于珊珊 张建军 李为民 杨先海

(1.河北工业大学机械工程学院， 天津 300130； 2.山东理工大学机械工程学院， 淄博 255000)

0 引言

机器视觉是涉及图像处理、机械、控制、光学、传感器、数字、计算机等领域的综合性技术[1]，已在工业、农业、航空航天、军事、医疗、天文气象、公共安全等领域得到了广泛应用[2-3]。目前，研究人员已在图像处理算法、动态性能、3D成像等方面展开了深入研究[4]。相比于工业生产的标准化，农业生产往往是复杂多变的室外环境，环境的未知性给机器视觉技术带来了诸多挑战。

视觉跟踪、视觉定位是机器视觉在农业中的应用场景之一，如农机导航、病虫草害控制、自动采摘等[5-6]。在采摘作业中，机器需要实时调整姿态，以实现跟踪定位的功能，球面并联机构是用于空间定位的经典机构,该机构动平台能够围绕空间中固定的一点，实现球面的工作空间，现已广泛应用于运动模拟器[7-8]、外科手术机器人[9]、精准定位[10-12]、仿生关节[13-16]、仿生眼[17-18]等球面工作空间领域。

随着科技的发展，对大角域工作空间的应用需求已变得越来越多，如目标多方位定位跟踪、未知环境探测等，国内外学者对球面并联机构的工作空间进行了大量的研究。BAI[19]针对球面并联机械手的工作空间进行了设计，将目标最优问题转换为非线性最小二乘问题，确定了空间设计最佳参数。杨健等[20]提出了一种智能遗传算法，对3-RRR球面并联机构进行参数优化，扩大了机构的有效工作空间。王超群等[21]以工作空间最大化为目标，对3-RRR球面并联机构进行了结构优化设计，使机构动平台实现了完整的球面工作空间。球面并联机构工作空间最大化一直是机构学领域的研究热点之一[22-24]。与传统球面并联机构相比，球面解耦并联机构因其解耦特性，具有各支链运动互不影响的特点，实现其工作空间最大化比较容易。

针对农业生产领域机器视觉对大工作空间的需求，本文提出一种运动支链设计方法，并设计2种二自由度全球面工作空间并联视觉云台，以期解决现有二自由度球面解耦并联机构工作空间不足的问题，为机器视觉大工作范围在智能农业机器人领域的应用提供理论依据。

1 大工作空间并联视觉云台结构设计

二自由度球面解耦并联机构是一种具有实际应用价值的球面并联机构。图1为2R&PRR型二自由度球面解耦并联机构[25]，由2条运动支链组成：①转动支链，由转动副R1和R2组成。②直线输入支链，由移动副P和转动副R3、R4组成。

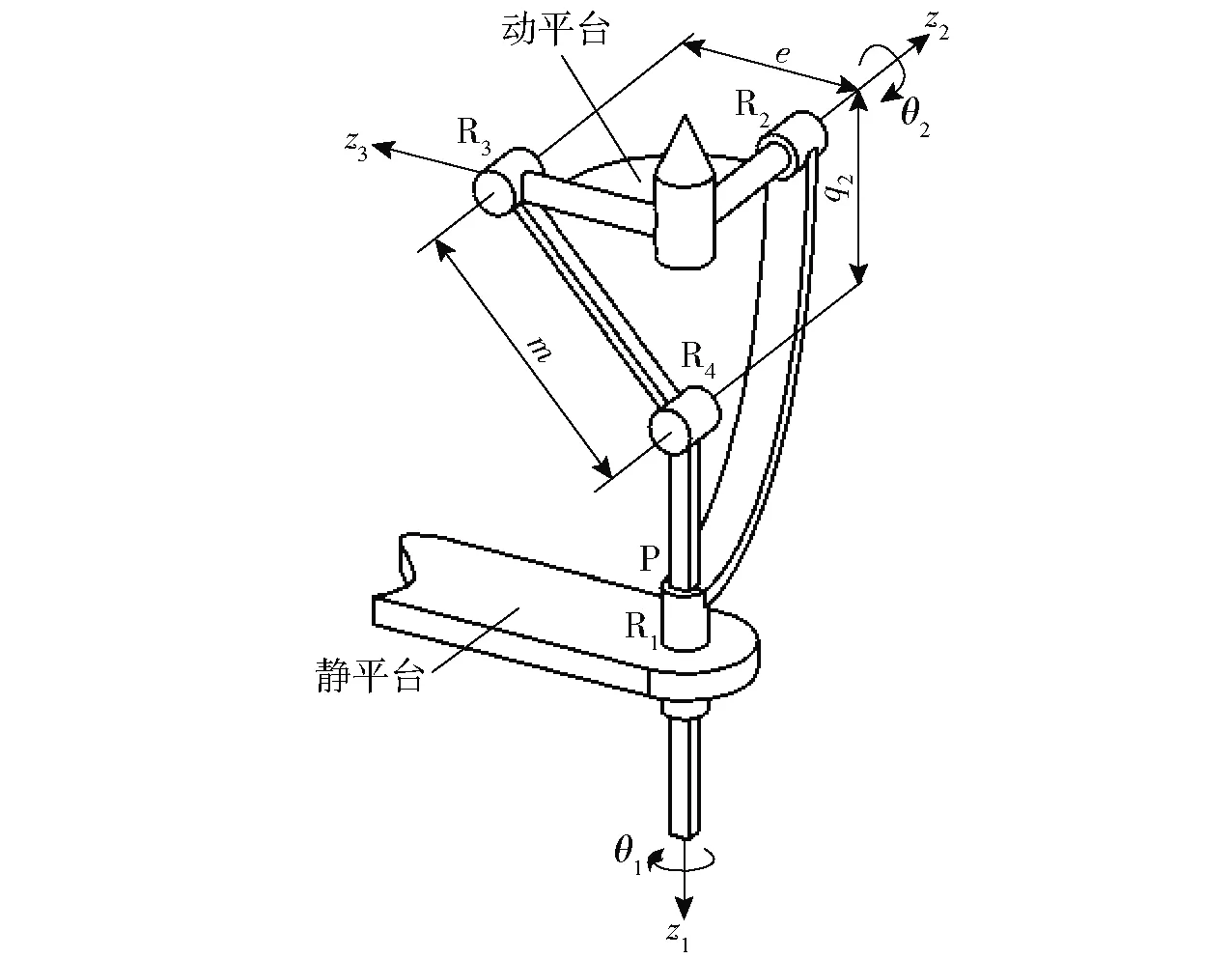
图1 2R&PRR型球面解耦并联机构Fig.1 2R&PRR spherical decoupled parallel mechanism

实际情况中，该机构转动支链可实现[0°, 360°]输出，而直线输入支链受转动副R2处摩擦圆的限制，其输出角范围小于[0°, 180°]，使得机构无法实现完整的球面工作空间。

1.1 运动支链设计

现有2R&PRR型球面解耦并联机构的输出角θ1的范围为[0°, 360°]，而输出角θ2的范围都小于[0°, 180°]，通过运动耦合后，现有2R&PRR型球面解耦并联机构的工作空间并不是完整的球面。因此，如何使输出角θ2的范围大于[0°, 180°]，成为全球面工作空间解耦并联机构研究需要解决的关键技术问题。

双摇杆机构的运动特性如下：当双摇杆机构主动摇杆与从动摇杆的杆长不同时，主动摇杆的摆角与从动摇杆的摆角也不相同。如图2所示，当以双摇杆机构较长的杆件CD作为主动摇杆，较短的杆件AB作为从动摇杆时，双摇杆机构可在较小摆角α下，实现较大的摆角β(β>α)，理论上摆角β的极限值可大于180°。

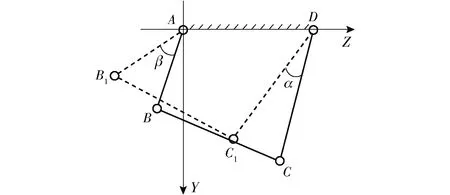
图2 双摇杆机构Fig.2 Double rocker mechanism

基于双摇杆的输入输出差异化设计二自由度全球面解耦并联机构，能够实现在较小输入角情况下，实现较大的输出角，理论上该输出角可大于180°。

根据二自由度解耦并联机构的结构形式(直线输入-转动输出)，对双摇杆机构进行变型设计，将双摇杆机构的输入杆件串联曲柄滑块机构，使转动输入转换为直线输入，以此得到P5R直线输入支链，如图3所示。

如图4所示，假设双摇杆机构的输入角为θ3，输出角为θ2，转动副R2的摩擦圆半径为ρ。如果P5R支链运动过程中杆件R4R5所在的直线与转动副R2的距离小于或等于摩擦圆半径ρ，则机构处于局部奇异位形，无法继续运动。因此，为使双摇杆机构输出角θ1大于180°，运动过程中杆件R4R5所在的直线不能与转动副R2处的摩擦圆相交，根据点线距离公式可得

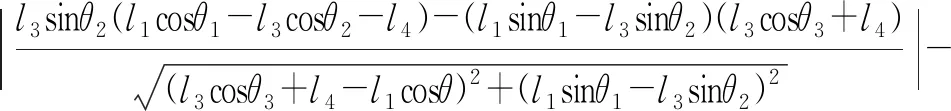
(1)

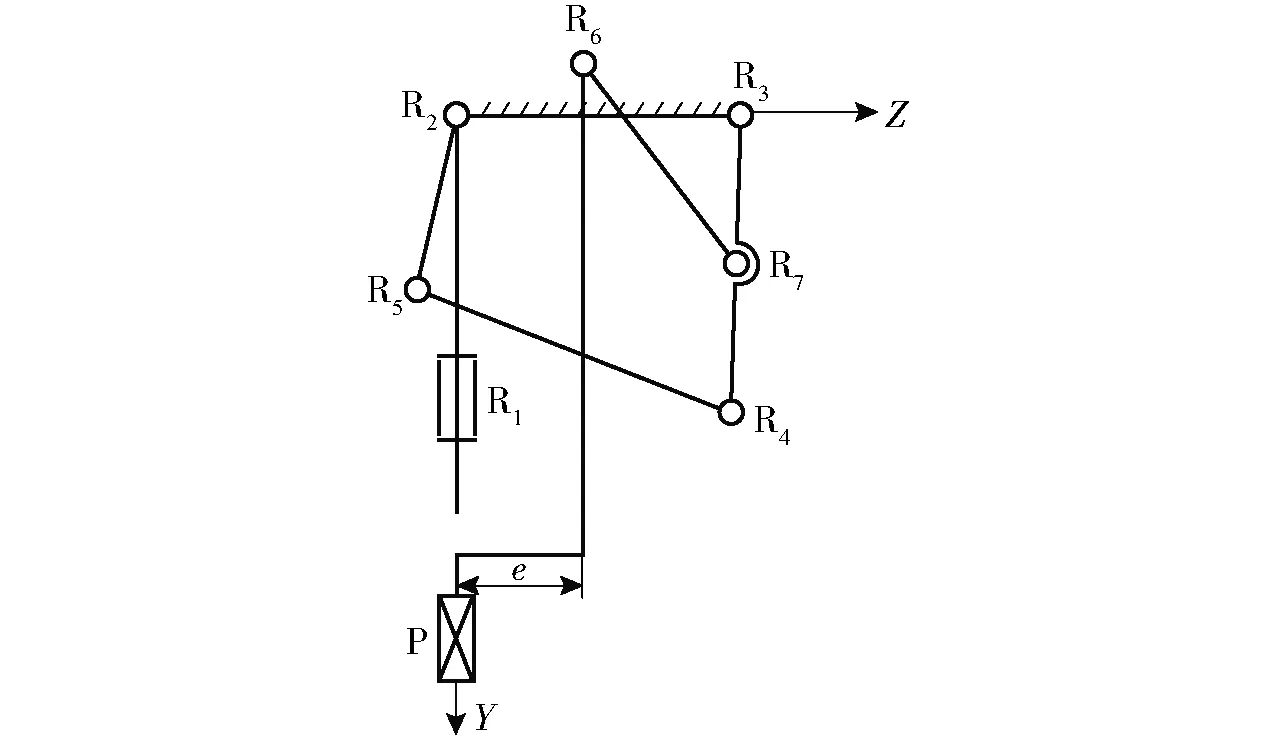
图3 P5R直线输入支链Fig.3 P5R linear input chain

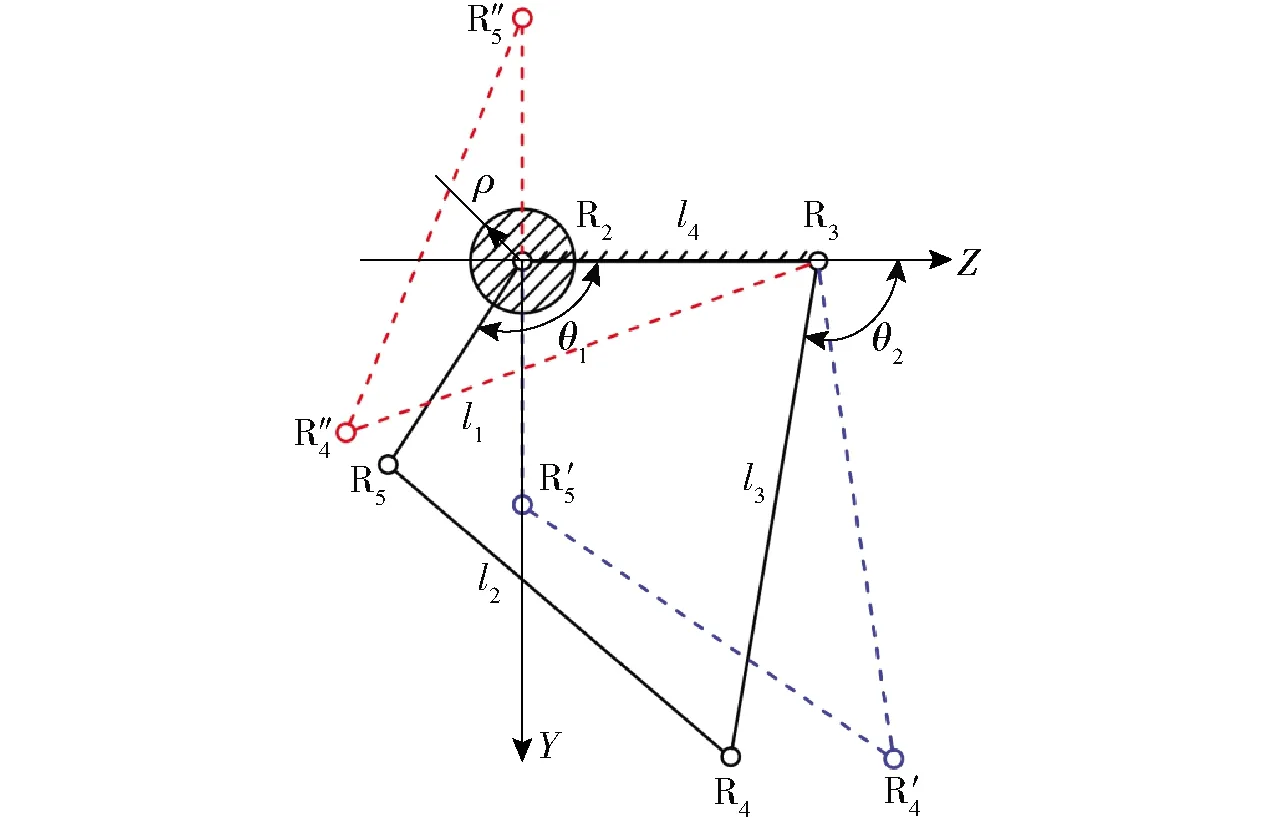
图4 双摇杆机构极限位置Fig.4 Limited position of double rocker mechanism

如图2所示，如果双摇杆机构的输入杆件趋于无限长，即点D处于无穷远处，则点C的运动轨迹由圆弧转换为直线，以此得到PRR直线输入支链，如图5所示。现有2R&PRR型球面解耦并联机构的直线输入支链同样也是曲柄滑块机构，其输出角极限值不能大于180°的原因是滑块的移动方向与转动副R2之间没有偏置距离，即偏置曲柄滑块机构在一定约束条件下，也可实现输出角大于180°。

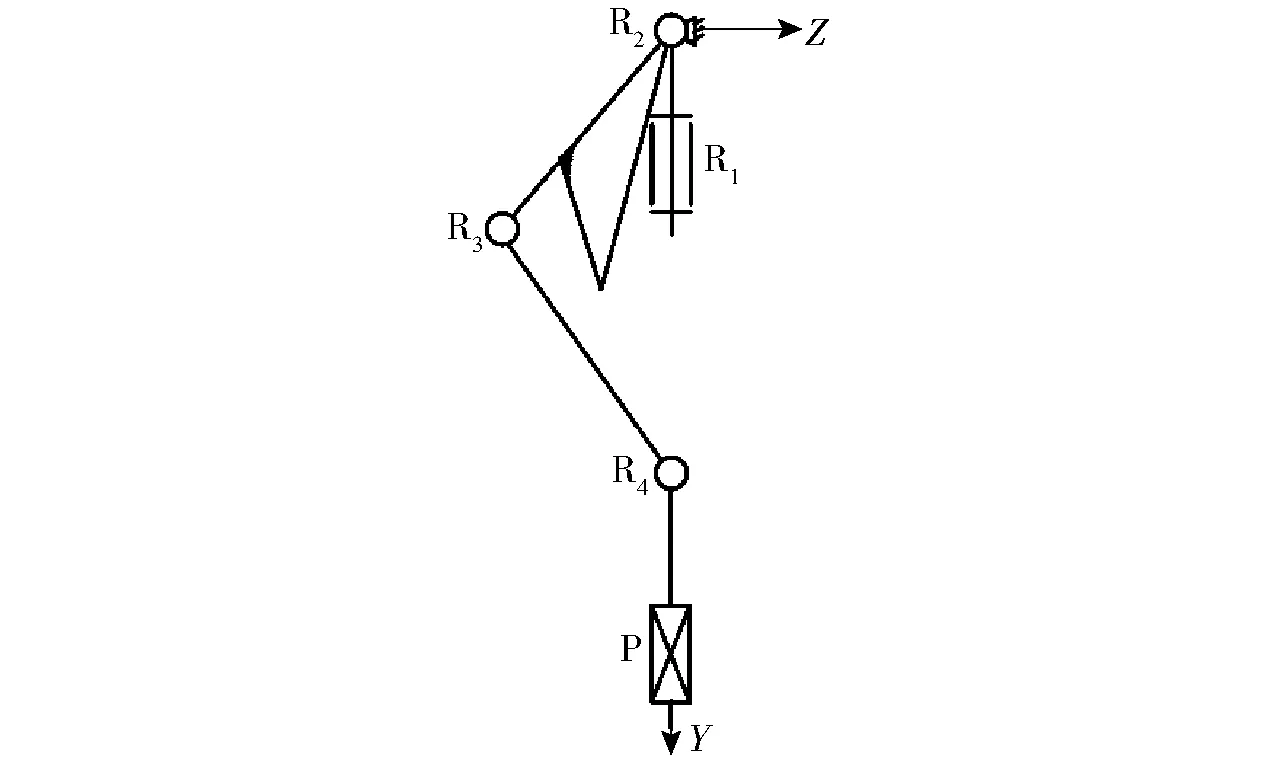
图5 PRR直线输入支链Fig.5 PRR linear input chain

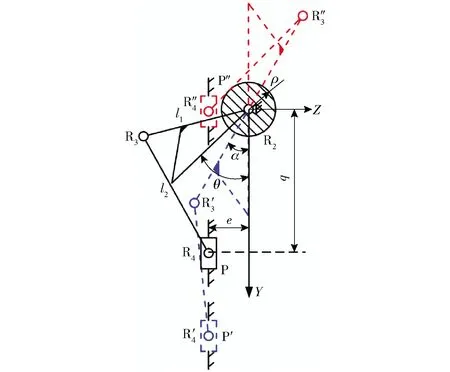
图6 偏置曲柄滑块极限位置Fig.6 Limited position of offset crank slider

如图6所示，假设偏置曲柄滑块输出角为θ，移动副P的输入量为q，移动副P与转动副R2在竖直方向的距离为e，转动副R2处的摩擦圆半径为ρ，动平台与杆件R2R3的夹角为α。同样，为满足PRR支链的输出角θ大于180°，运动过程中杆件R3R4所在的直线不能与转动副R2处的摩擦圆相交，根据点线距离公式可得

(2)

1.2 并联视觉云台结构设计

图7 RR&P5R型全球面并联视觉云台Fig.7 RR&P5R decoupled parallel vision table with fully spherical workspace

基于P5R直线输入支链，所设计的并联视觉云台如图7所示。机构动平台通过2条运动支链与静平台相连：转动支链由转动副R1和R2组成，由于该运动支链由2个转动副组成，也称为RR运动支链；直线输入支链由移动副P和转动副R3、R4、R5、R6、R7组成，由于该运动支链由1个移动副和5个转动副组成，也称为P5R运动支链，该机构称为RR&P5R型全球面工作空间并联视觉云台。

基于PRR直线输入支链，所设计的并联视觉云台如图8所示。动平台通过2条运动支链与静平台相连：转动支链由转动副R1和R2组成，称为RR运动支链；直线输入支链由移动副P和转动副R3、R4组成，称为PRR运动支链。该机构称为RR&PRR型全球面工作空间并联视觉云台。

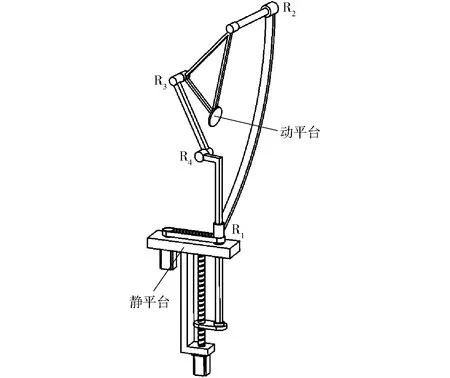
图8 RR&PRR型全球面并联视觉云台Fig.8 RR&PRR decoupled parallel vision table with fully spherical workspace

两种并联视觉云台均可实现完整的球面工作空间，如图9所示。

图9 完整球面工作空间Fig.9 Fully spherical workspace

2 机构位置分析

2.1 RR&P5R型机构

如图10所示，k表示RR&P5R型机构转动副R7在杆件L3上的位置，取值范围为(0，1)。则机构的构件几何关系可以表示为

(3)

(4)

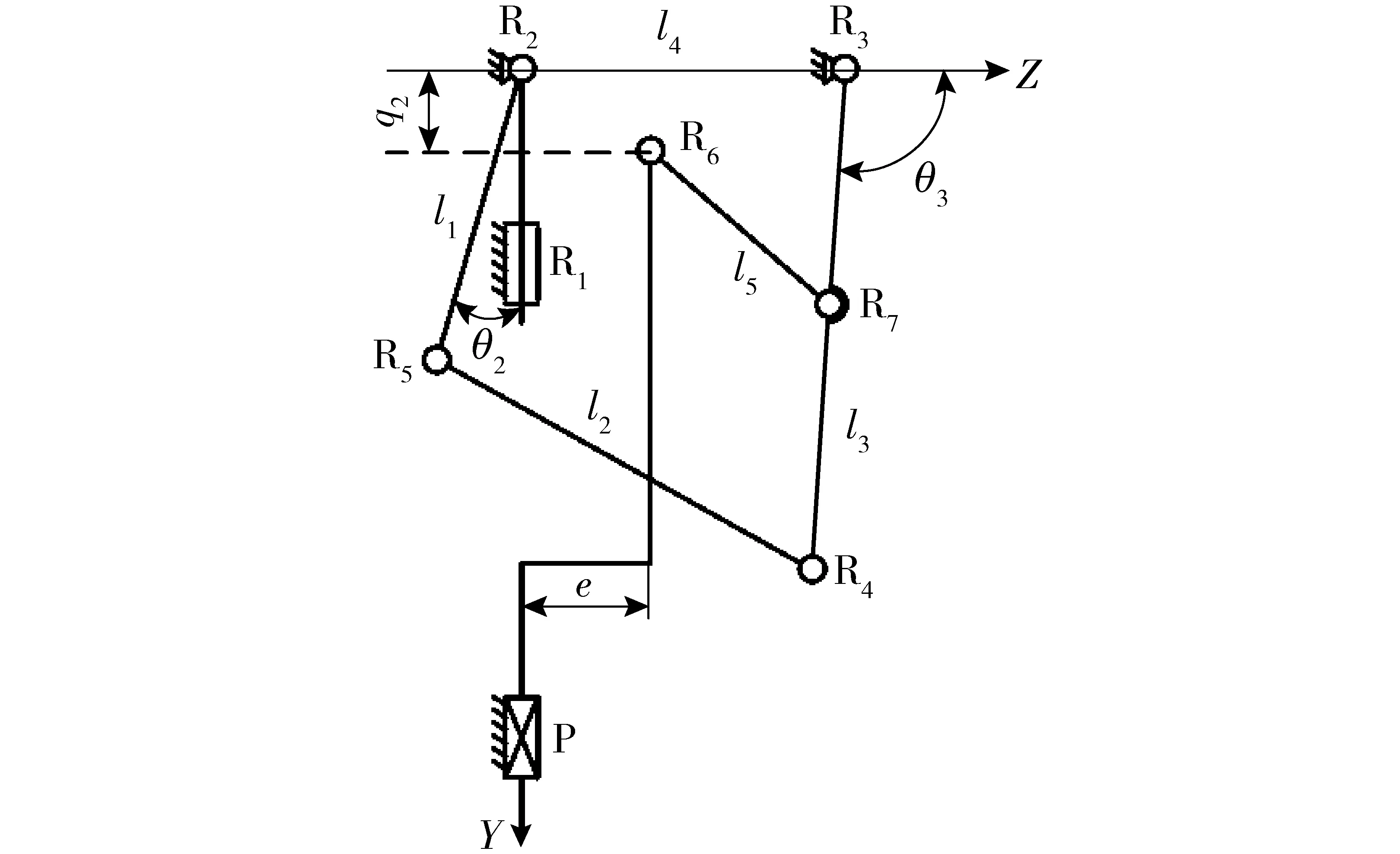
图10 RR&P5R型全球面解耦并联机构简图Fig.10 Schematic diagram of RR&P5R decoupled parallel mechanism with fully spherical workspace

根据式(3)、(4)，可得RR&P5R型机构位置解为

(5)

其中C=l4-l3sinθ3D=l3cosθ3

2.2 RR&PRR型机构

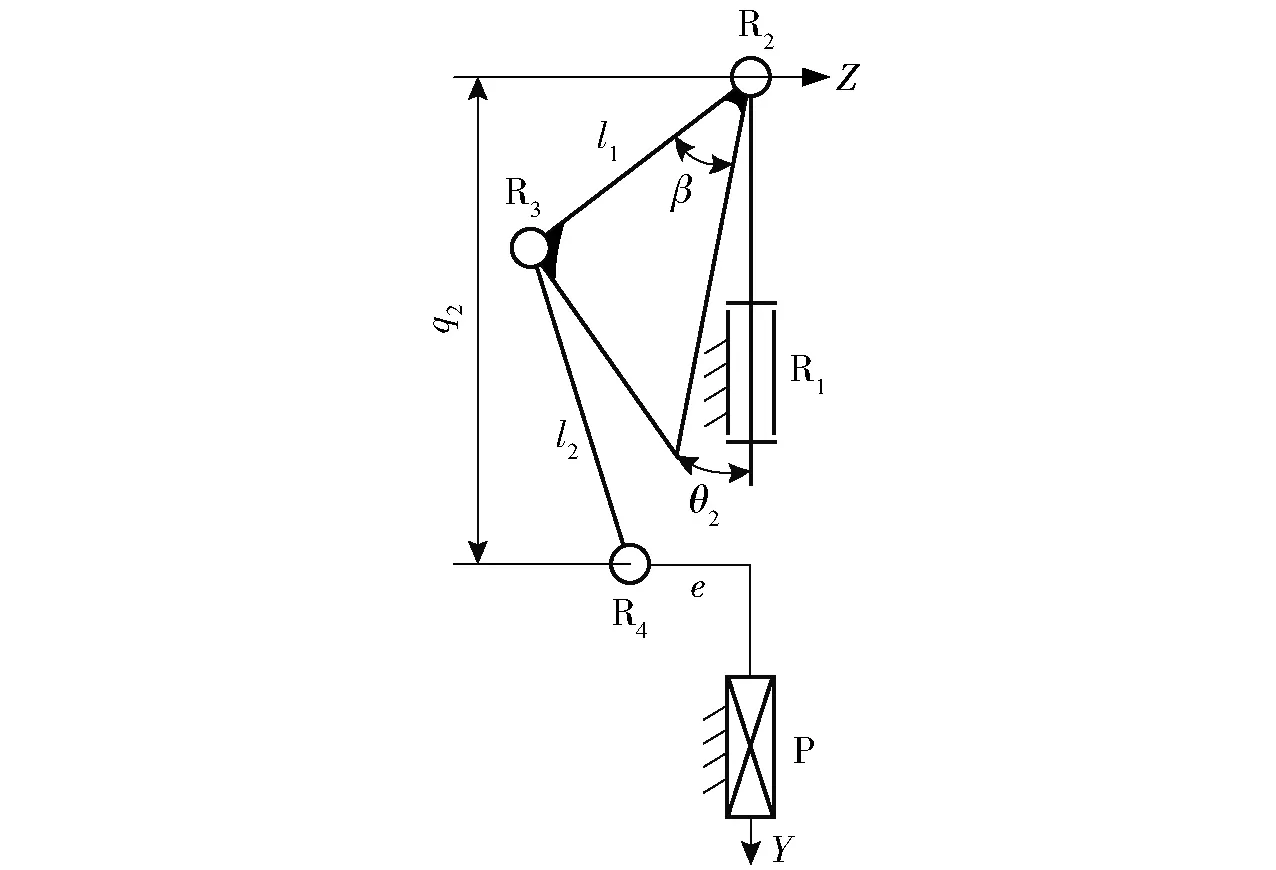
图11 RR&PRR型全球面解耦并联机构简图Fig.11 Schematic of RR&PRR decoupled parallel mechanism with fully spherical workspace

如图11所示，β为动平台所在平面与杆件L1之间的夹角，机构构件之间的几何关系可表示为

(6)

根据式(6)可得RR&PRR型机构位置解为

(7)

3 尺寸优化与输入输出特性

3.1 尺寸优化

如图10所示，当转动副R7越靠近转动副R3，其力臂越短，机构适合轻载模式，反之，如果转动副R7越靠近R4，其力臂越长，机构更适合重载模式。本文仅研究转动副R7处于杆件L3中点处的情况，即k=0.5，优化目标为移动副P的位移最小。RR&P5R机构优化结果如图12所示，l1、l2、l3、l4、l5、e最优比约为1.68∶2.78∶4.03∶2∶1.98∶1.5。

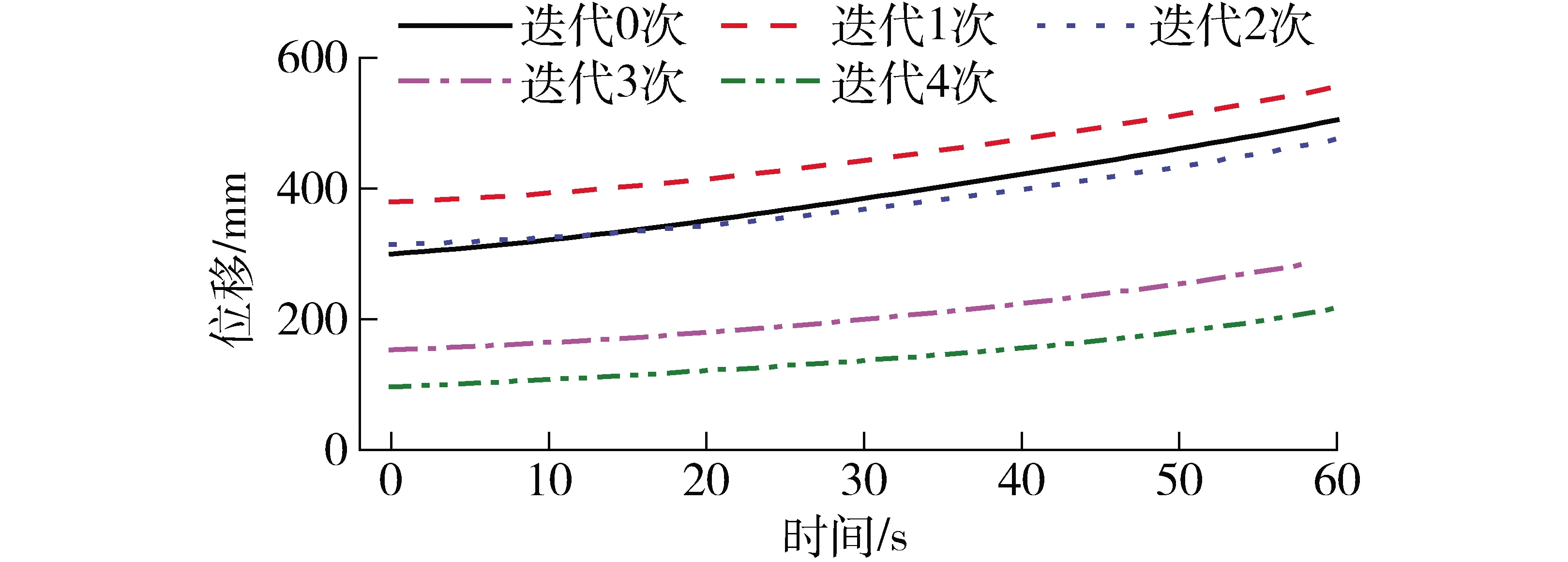
图12 RR&P5R机构优化曲线Fig.12 Optimization curves of RR&P5R mechanism

如图11所示，夹角β=30°，根据式(2)计算得出emin=51.89 mm。e选取51.89、100、150、200 mm对机构进行优化分析，优化目标为移动副P的位移最小，当e=51.89 mm时存在最优结果，如图13所示。RR&PRR机构杆长l1、l2最优比约2∶1.83。

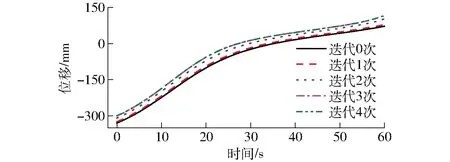
图13 e=51.89 mm时RR&PRR机构优化曲线Fig.13 Optimization curves of RR&P5R mechanism when e=51.89 mm

3.2 输入输出特性

模拟并联视觉云台的实际使用环境，机构动平台应为等速等距输出，则RR&P5R机构和RR&PRR机构输入情况如图14所示。如图14a所示，RR&P5R型机构的输入速度呈现递增规律，而RR&PRR型机构幅值波动较大。如图14b所示，RR&P5R型机构输入力比较小且平稳，而RR&PRR型机构输入力较大且变化较大。通过比较可以明显看出，RR&P5R型机构的输入输出特性更优。

4 静力学分析

如图15所示，建立P5R支链的静力学分析简图。假设机构杆件的质量以及杆件之间的摩擦忽略不计，机构处于低速运动，经过静力学分析，杆件BC为二力杆。假设转动副A点处存在恒定的扭矩载荷M，对应移动副P的输入驱动力为FP。各杆件受力如图16所示。

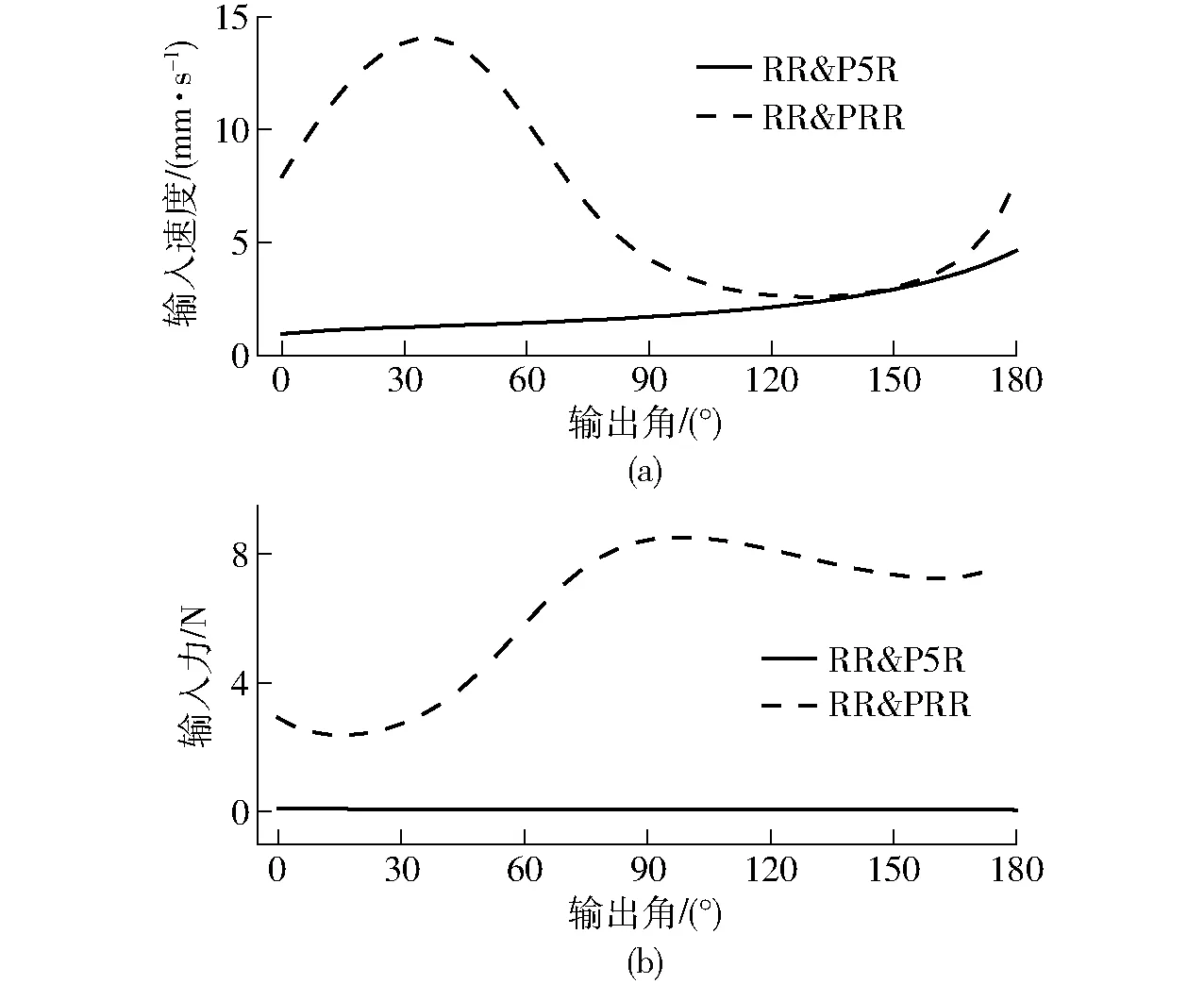
图14 RR&P5R和RR&PRR并联机构输入曲线Fig.14 Input curves of RR&P5R and RR&PRR parallel mechanism

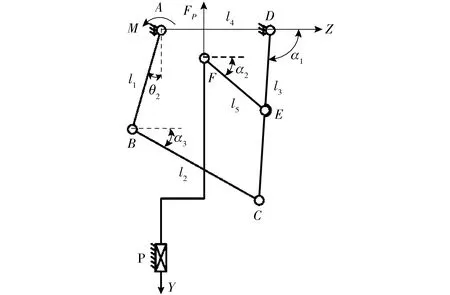
图15 P5R支链静力学分析图Fig.15 Static analysis of P5R kinematic chain

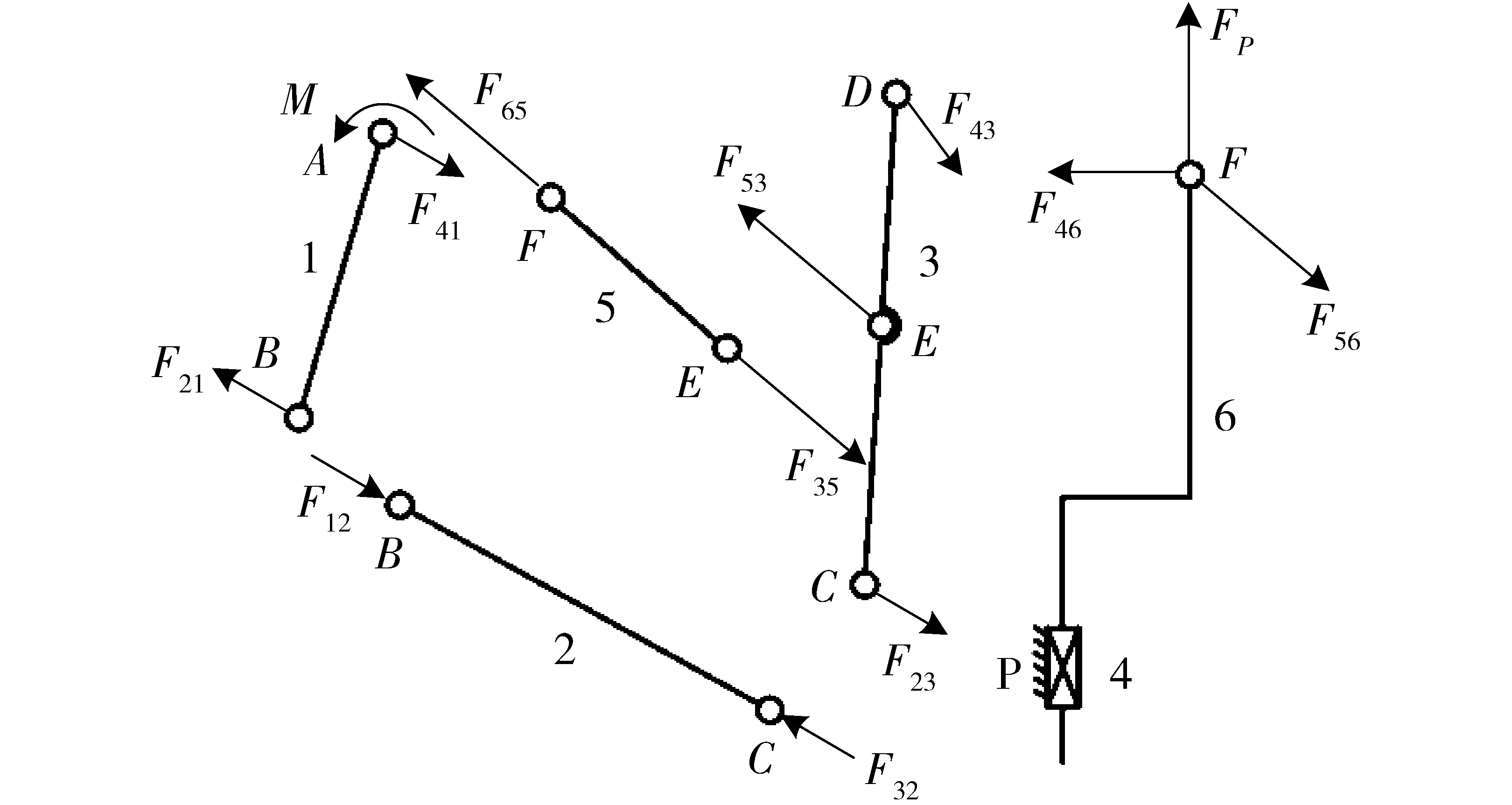
图16 各杆件受力图Fig.16 Force diagram of each member bar

杆件AB静力学平衡方程为

M+F21l1cos(θ2-α3)=0

(8)

F21+F41=0

(9)

杆件BC静力学平衡方程为

F12+F32=0

(10)

杆件CD静力学平衡方程为

F23+F43+F53=0

(11)

杆件EF静力学平衡方程为

F35+F65=0

(12)

杆件FP静力学平衡方程为

FP+F46+F56=0

(13)

将以上静力学平衡方程整理可得各铰链处约束力如下：

点A、点B、点C约束力为

(14)

点E、点F约束力为

(15)

点D约束力为

(16)

驱动力为

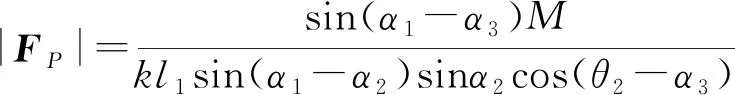
(17)

假设点A处扭矩载荷M为2 000 N·mm，RR&P5R机构杆长按照最优比例l1∶l2∶l3∶l4∶l5∶e≈1.68∶2.78∶4.03∶2∶1.98∶1.5取值，即l1=168 mm，l2=278 mm，l3=403 mm，l4=200 mm，l5=198 mm，e=150 mm。则机构各铰链处的约束力如图17所示。从图17可以看出，点A、点B、点C处的铰链约束力较小，而点D、点E、点F处的铰链约束力较大。

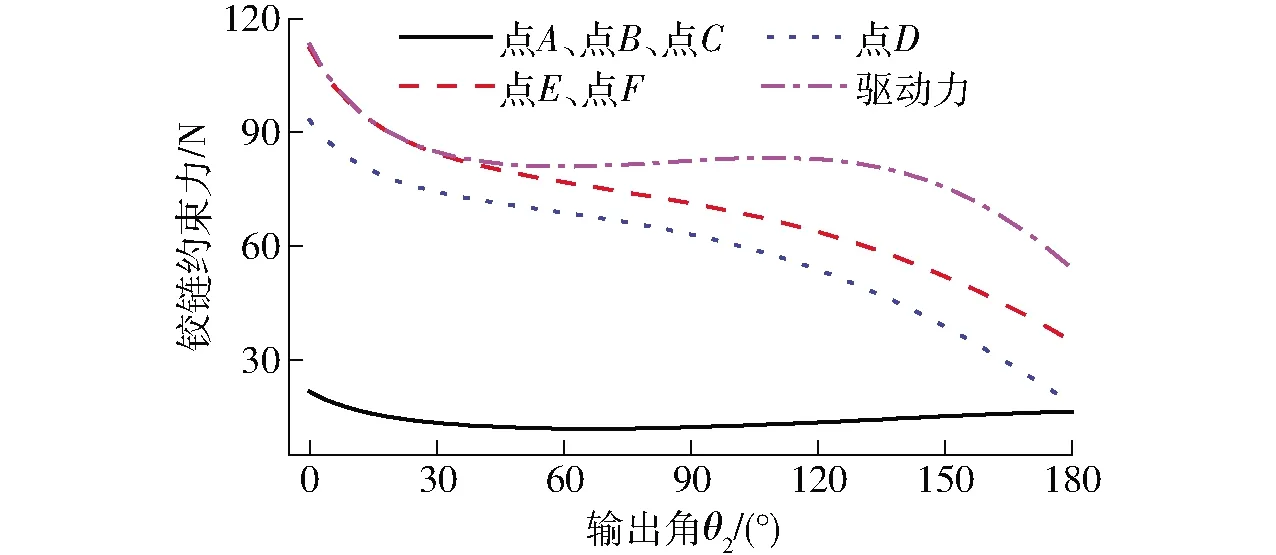
图17 各铰链处约束力Fig.17 Restraining force at each hinge

图19 各转动副在X、Y、Z方向的位移偏差Fig.19 Displacement deviation of each revolute joint in X, Y and Z directions

5 有限元分析

设计了RR&P5R型并联视觉云台。以杆件R2R3在Z轴方向的距离为基准尺寸，距离为200 mm，其他杆长按照比例l1∶l2∶l3∶l4∶l5∶e≈1.68∶2.78∶4.03∶2∶1.98∶1.5进行设计。杆件R2R5采用空心圆管设计，截面直径为20 mm，壁厚为2 mm；其余各杆件均采用空心方管设计，截面边长为20 mm，壁厚为2 mm。

为了分析载荷对RR&P5R机构运动精度的影响，利用ABAQUS软件对RR&P5R机构进行有限元分析。选用的计算单元为 C3D20R，模型材料为钢材料，材料参数：弹性模量E=210 GPa，泊松比υ=0.3，密度为7 850 kg/m3。

第1次模拟分为2步：①对转动副R2处施加2 000 N·mm的扭矩载荷，移动副P施加零位移约束。②设置移动副P的Y向位移34 mm，其他设置不变。如图18所示，机构最大应力点在移动副杆件的拐角处，达到118.10 MPa，但未超过材料屈服极限。

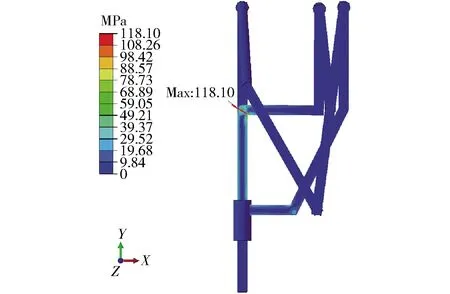
图18 RR&P5R机构应力云图Fig.18 Stress cloud diagram of RR&P5R mechanism

为检验载荷对弹性机构位移偏差的影响，进行第2次模拟：①对转动副R2处施加扭矩2 N·mm。②与第1次模拟中的设置相同。各转动副在X、Y、Z方向的位移偏差如图19所示，各转动副在空间的位移偏差如图20所示。由图19、20可知，在机构初始位置处各运动副位移偏差最大，运动副R5的偏差超过10 mm。

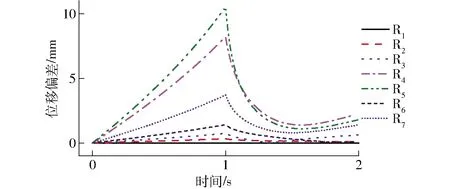
图20 各转动副的空间位移偏差Fig.20 Spatial displacement deviation of each revolute joint

6 结论

(1)针对农业机器人对大角域视觉工作空间的需求，提出一种可用于构建二自由度全球面工作空间解耦并联机构的运动支链设计方法，该支链具有直线输入和旋转输出特性，并衍生出2种可行的支链构型P5R和PRR。基于这2种支链，设计了2种二自由度全球面工作空间并联视觉云台RR&P5R和RR&PRR，并给出了这2种机构的位置分析式。

(2)通过尺寸优化，得到RR&P5R型机构的最优杆长比为l1∶l2∶l3∶l4∶l5∶e≈1.68∶2.78∶4.03∶2∶1.98∶1.5；RR&PRR型机构最优杆长比为l1∶l2∶e≈2∶1.83∶0.5。RR&P5R型并联机构具有更优的输入输出特性。

(3)通过有限元分析，研究了RR&P5R型机构的强度和运动精度，结果表明，该机构强度满足要求，但各杆件累积弹性变形导致运动副的位移偏差较大。在实际应用中，可通过适当增加各杆件的横截面来提高运动副的运动精度。