基于并联深度信念网络的数控机床热误差预测方法

杜柳青 余永维

(重庆理工大学机械工程学院， 重庆 400054)

0 引言

热误差引起的数控机床加工误差占比达40%～70%[1]。热误差具有准静态时变、非线性、衰减延迟及耦合等特征，建立机床热误差和温度之间的准确映射关系是热误差控制的难点[2-5]。反向传播(Back propagation，BP)网络[6-7]、径向基函数(Radial basis function，RBF)网络[8]、灰色系统理论[9]等浅层网络理论建立的传统热误差模型存在以下不足：浅层模型采用人工特征，其适应性和鲁棒性不强[10-12]；浅层模型难以表征大数据下监测信号与热误差之间的映射关系，模型精度尚待提高。

针对现有技术的不足，利用深度学习强大的特征自学习和大数据建模能力[13-19]，本文提出一种基于并联深度信念网络的数控机床热误差预测与补偿方法，以自动提取数控机床温度数据深层特征，准确表征大数据下监测温度信号与热误差之间复杂的映射关系，提高热误差预测与补偿精度、实时性和鲁棒性。

1 主轴热误差预测原理

与传统方法相比，深度学习方法依靠数据驱动，能自动地从数据中提取特征(知识)，对于分析非结构化、模式不明多变、热误差等大数据具有显著优势[20-25]。

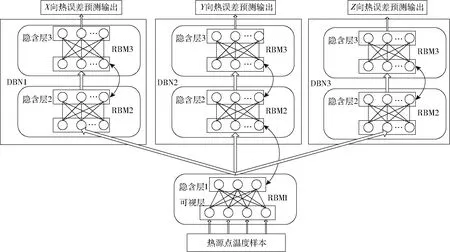
图2 数控机床深度学习热误差预测模型Fig.2 Thermal error prediction model for deep learning of CNC machine tools

本文提出的基于并联深度信念网络的数控机床热误差预测与补偿原理如下：首先采集样本数据，在数控机床上选取热源测量点，检测热源测量点的温度和对应时间点的主轴热误差；建立基于并联深度信念网络的深度学习热误差预测模型，利用采集的样本数据训练深度学习热误差预测模型；然后，实时检测数控机床热源测量点的温度，并输入到训练后的深度学习热误差预测模型，实时预测热误差；最后，将预测的热误差作为数控机床坐标系原点的补偿平移量，通过坐标系原点偏移实现热误差实时补偿(图1)。该方法能够准确表征大数据情况下监测温度信号与热误差之间复杂的映射关系。

图1 数控机床热误差预测与补偿原理图Fig.1 Thermal error prediction and compensation principle of CNC machine tools

2 热误差预测模型

2.1 深度学习热误差预测模型

数控机床深度学习热误差预测模型由3个深度信念网络(Depth belief network，DBN)DBN1、DBN2、DBN3并联而成。3个深度信念网络有相同的网络结构和不同的权值，并共享1个限制玻尔兹曼机(Restricted Boltzmann machine，RBM)，即RBM1层。DBN1、DBN2、DBN3分别预测主轴在径向方向(2个)和轴向方向(1个)的热误差。建立数控机床深度学习热误差预测模型，如图2所示。

2.2 并联深度信念网络结构构建

每个深度信念网络均包含1个可视输入层、3个限制玻尔兹曼机RBM隐含层(即RBM1、RBM2、RBM3)和1个输出层。

可视输入层神经元数量与设置的关键热源点数量相同；输出层神经元数量为1，其输出为主轴在某个方向上的热误差预测值。

输出层神经元数量为1个，其输出分别为主轴在X轴方向、Y轴方向或Z轴方向上的热误差。

每个RBM隐含层的神经元数量与热源关键点数r、样本数据量N有关。每个RBM隐含层的神经元初始数量p0均设定为p0=r/2，然后以步长为S逐步增加，以模型预测均方根误差最小为判断指标最终确定每个RBM隐含层的神经元数量，各DBN隐含层神经元数量确定方法如图3所示。

2.3 并联深度网络训练方法

提出一种初始权值共享的并联深度网络训练方法，首先采用对数散度无监督学习方法，预训练模型中的其中一个深度信念网络DBN1，获得其网络初始权值，深度信念网络DBN2、DBN3共享该初始权值。深度信念网络对数散度无监督学习方法如图4所示。

(1)将DBN的每一层神经元随机初始化为0或1，不同层之间的神经元连接权值wij(i=1,2,…;j=1,2,…)置为(0,1)范围的任意值。首先预训练RBM1。

(2)利用温度样本数据由可视层神经元vi算出隐含层神经元hj，则连接权值wij的正向梯度为Hij=vihj。

(3)由隐含层神经元hj反向计算得到的可视层神经元为v′i，则连接权值的反向梯度为H′ij=v′ihj。

(4)更新连接权值：wij=wij+ε(Hij-H′ij)，其中ε为学习速率，一般设定为0～1。

(5)利用采集的温度样本数据循环训练RBM1网络，不停迭代，直到收敛，即Lij-L′ij≤δ，Lij、L′ij为似然函数值，δ为一极小收敛阈值，一般设定为小于0.01。

(6)同样方法，依次预训练RBM2和RBM3的连接权值。

(7)将训练完成的DBN1参数对应赋值给DBN2、DBN3，实现初始权值共享。

然后，采用BP算法分别微调生成3个深度信念网络的最优权值。利用标签数据反向修正预训练获得的初始权值；然后，正向测试新得到的各层权值参数；如此反复，直到模型预测的均方根误差E收敛为止。

均方根误差E收敛判别式为

(1)

式中t——训练次数

λ——极小阈值，一般设定为小于0.01

3 实验与结果分析

3.1 数据采集

实验以XHA6120型动梁式大型龙门五面加工中心为研究对象。根据该龙门加工中心的结构、工况及热源分布，将热源关键点设置在机床发热较集中部位或其附近，采用18个温度传感器检测温度，温度关键点编号为T1～T18。

测量龙门加工中心主轴在径向方向和轴向方向的3个热误差：ex、ey、ez。测量方法如图5所示。采用德国米依公司ES-U1型电涡流传感器，其量程为1 mm，分辨率为0.02 μm，线性度为±1%，能够满足本实验的精度要求。

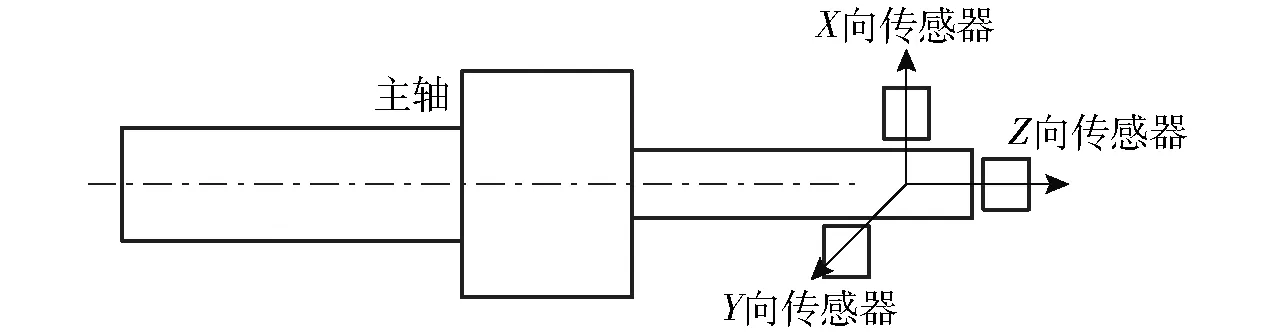
图5 龙门加工中心主轴热误差测量方式Fig.5 Measurement method of thermal error

模拟龙门加工中心连续循环加工状态、主轴旋转、进给轴移动、冷却液循环，每隔5 min记录一次各温度传感器的数值和主轴位移传感器的数值，共采集150组温度及热误差作为样本数据。将150组样本数据归一化，用于深度学习预测模型的训练和验证，计算式为

(2)

式中a′i——各样本数据归一化后的值

ai——各样本数据原始值

amax——各类型样本数据的最大值

amin——各类型样本数据的最小值

3.2 模型结构确定及训练

可视输入层神经元数量与设置的关键热源点数量相同，均为18个。DBN1的输出为主轴在X轴方向上的热误差；DBN2的输出为主轴在Y轴方向上的热误差；DBN3的输出为主轴在Z轴方向上的热误差。

每个RBM隐含层的神经元数量对模型的预测精度和泛化能力影响较大。神经元数量过少会造成温度特征信息的丢失，导致特征提取不完整，预测精度低。增加神经元数量，预测精度会提高，但神经元数量过多会造成模型的泛化能力差。RBM隐含层的神经元数量确定步骤为：

(1)根据热源关键点数r=18和采集的样本数据量L=150，先设定每个RBM隐含层的神经元初始数量均为p0=⎣r/2」，该式含义为取r/2的整数部分。p0为初始值9时，计算得到的均方根误差为0.102。

(2)保持RBM2和RBM3隐含层的神经元数量固定不变，以步长S=2逐渐增加RBM1隐含层的神经元数量p1。当p1=21时，模型预测的均方根误差达到最小值0.025，将p1=21确定为RBM1隐含层的神经元数量。

(3)同理，在确定RBM2的时候，RBM1的神经元数量固定在21，RBM3的神经元数量固定在9，最终确定RBM2的神经元数量为21。在确定RBM3的时候，RBM1的神经元数量固定在21，RBM2的神经元数量固定在21，最终确定RBM3的神经元数量为19。

采用对数散度无监督学习方法，首先预训练RBM1，学习速率ε设定为0.1，迭代收敛阈值设定为0.005，经990次迭代后完成预训练。同理，分别经860次和1 100次迭代后完成对RBM2和RBM3的预训练。将训练完成的DBN1参数对应赋值给DBN2、DBN3，实现初始权值共享。

用标签样本数据、采用BP算法分别微调生成3个深度信念网络的最优权值。均方根误差E的收敛阈值λ设为0.005，微调学习速率设为0.1。3个深度信念网络分别经35、46、39次迭代后完成权值微调，此时3个并联的深度信念网络的预测均方根误差分别为0.01、0.015、0.012。

经过上述预训练和调优后，预测模型构建完成，各模型参数成功获得。然后将实时检测的一系列温度输入预测模型，用来预测对应的主轴热误差值。

3.3 实验结果分析

实时测量28组该龙门加工中心关键热源点温度，输入该深度学习预测网络预测主轴热误差，获得了高精度的热误差预测结果，如图6所示。模型预测的热误差均方根误差为2.2 μm，平均绝对百分比误差为7.8%，实时数据预测与训练样本数据预测的性能指标基本一致，说明深度学习热误差预测模型具有非常好的泛化能力。

图6 热误差预测及补偿Fig.6 Prediction and compensation of thermal error

该龙门加工中心主轴在X、Y、Z3个方向上的热误差分别为ex、ey、ez，将此作为机床坐标系原点的补偿平移量，机床坐标系原点在X、Y、Z轴3个方向上分别平移-ex、-ey、-ez，补偿后的X、Y、Z方向的最大残差分别为2.5、3.0、2.5 μm，表明本文方法能够实现机床热误差的高精度补偿。

利用该龙门数控机床数据样本构建传统支持向量机(Support vector machine，SVM)预测模型和BP神经网络预测模型。对比实验中，SVM预测模型和BP神经网络预测模型的X、Y、Z方向热误差预测效果如图7所示，二者的均方根误差分别为4.9、5.3 μm，平均绝对百分比误差分别为22%、33%，二者的预测准确性均远低于本文方法，本文提出的深度层次结构能够比浅层网络更准确提取出蕴含在温度数据中的本质特征信息，所以本文方法的预测精度比传统方法更高，鲁棒性更好。

图7 SVM模型和BP模型的主轴热误差预测结果Fig.7 Thermal error prediction based on SVM model and BP model

4 结论

(1)提出一种基于3个子深度信念网络并联的深度学习预测模型，设计的各子深度信念网络采取共享网络结构与初始权值的策略，大大提高了模型训练的效率。

(2)基于并联深度信念网络的主轴热误差预测与补偿方法能够自动提取数控机床温度数据深层特征，准确建立热误差与数控机床温度测点的非线性映射关系，实现了热误差状态的智能预测与补偿。

(3)并联深度信念网络预测模型解决了传统浅层网络方法预测精度不高、鲁棒性差等问题，实验获得主轴热误差预测值的均方根误差为2.2 μm，优于传统的SVM和BP预测方法。本文方法在提高预测准确性的同时，显著提高了热误差补偿的适应性和鲁棒性。