“一题一课”：让高三数学复习走向素养落实①

张文海

(江苏省苏州实验中学 215011)

1 问题的背景

当前，高三数学课堂的教学现状是在高一高二拼命压缩赶进度，留出一年甚至一年半的时间进行反复练、练反复，老师和学生陷入无尽的题海，大多数课堂呈现重“教”轻“学”、重“知”轻“能”、重“结果”轻“过程”的现象．不仅师生双方感到疲惫不堪，而且教学效果不理想．对于一些典型问题和典型错误，学生是屡做屡错，屡做屡犯；对于一些重点问题的处理方法，学生不能深刻地理解和掌握．笔者曾经在本学期教学中做过这样的测试，一周前让学生在课堂上限时15分钟解一道大题(知识可以是解析几何、导数、数列)，批改统计后认真评讲，课后也要求学生订正整理，一周后再让学生在课堂上限时15分钟独立完成该原题，结果能完全解答正确的人数与之前相比，没有太大的变化，尤其值得关注的一点，原来怎么想怎么做的，后来还是怎么想怎么做的，学生的思维结构没有发生任何变化.究其原因，还是在学生的头脑里，知识是孤立的、零散的存在，没有形成一个网络，也没能建立成一个完整的知识体系．还有就是在评讲时，没能让学生的思维卷入到课堂中，没能真正建立自己的理解；这样的思维记忆就是短暂的，不能长久，也就造成目前教学中出现教师讲过多遍，学生依然不会的困境．为了改变目前这种现状和困境，下面以“椭圆中斜率之和问题探究”为例，通过“一题一课”模式进行的实践与思考与同仁交流．

2 “一题一课”模式

美国著名数学家G·波利亚说：“一个专心的认真备课的教师能够拿出一个有意义的但有不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域．”苏联数学教育家奥加涅也说过：“必须重视，很多习题潜在着进一步扩展其教学功能、发展功能和教育功能的可能性．”由此可见，解题教学在数学课堂教学，尤其在高三数学复习中的重要性，设计得当的解题教学，往往能够起到事半功倍的效果．

“一题一课”模式就是对一道题或一个材料进行深入研究，认真琢磨其本质，通过纵横联系，将孤立问题“串”起来；通过课外拓展，让学生思维“飞”起来．基于学情，科学、合理、有序地组织学生进行相关的数学探索活动，从而完成一节课的教学任务，以此达成多维目标的过程．

3 教学案例

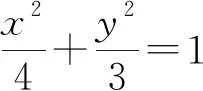
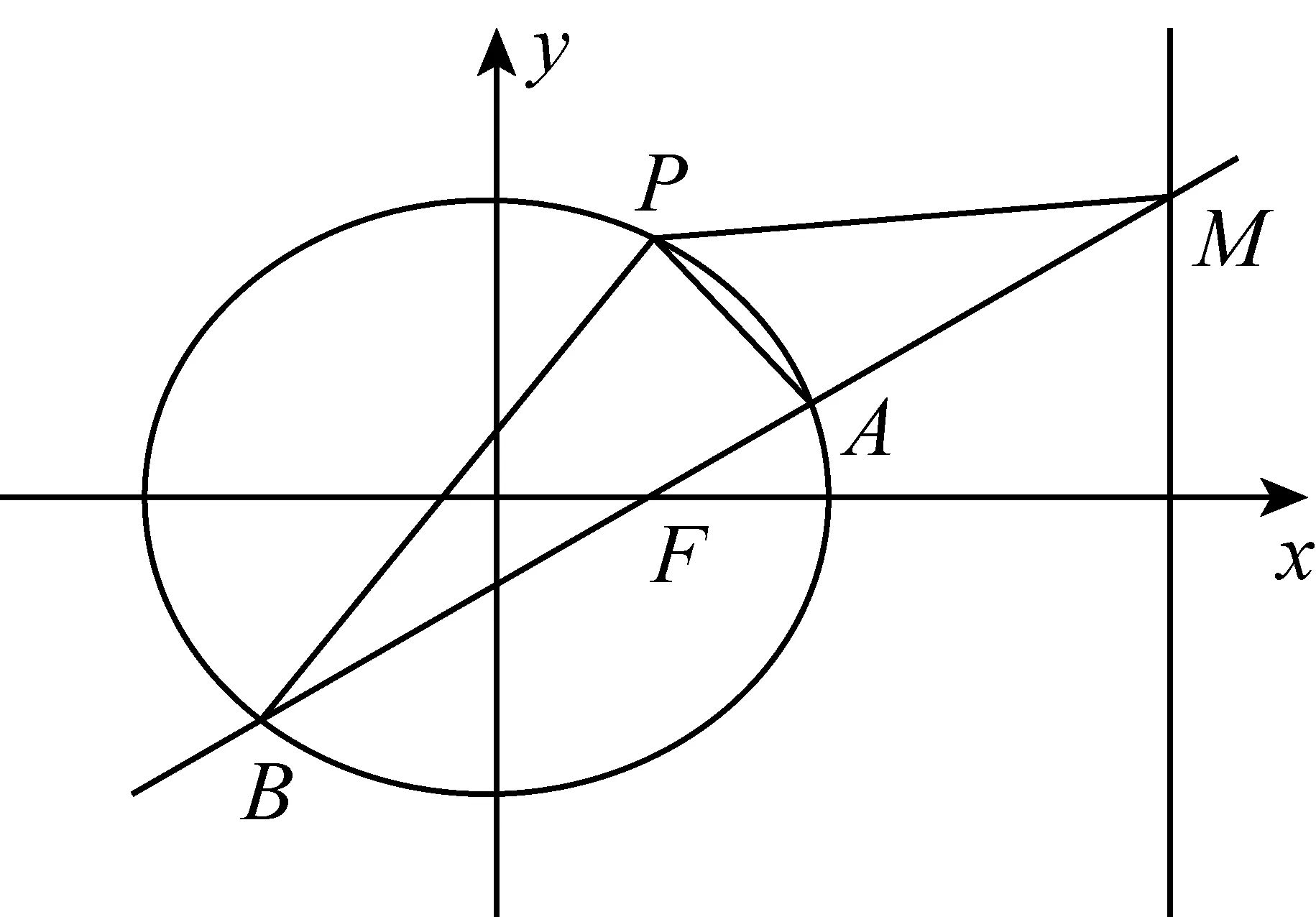
分析：本题研究的是直线PA，PB，PM的斜率k1，k2，k3之间的关系，因为斜率与点P，A，B，M的坐标有关，而点A，B，M是直线AB与椭圆和直线l的交点，所以只需设出直线AB的方程，建立方程组，就可以解出所需要点的坐标，进而找到k1，k2，k3之间的关系．

解：因为直线AB与直线l相交于点M，

所以斜率存在，

故可设直线AB的方程为y=k(x-1)．

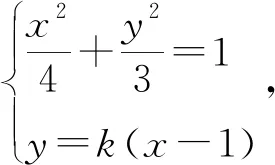
整理得(4k2+3)x2-8k2x+(4k2-12)=0，

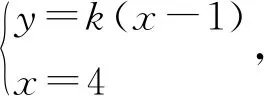
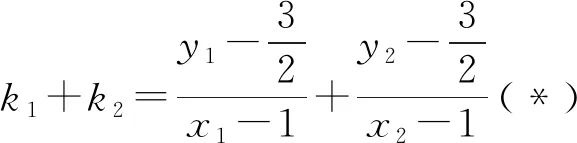
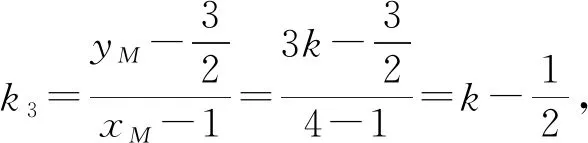
故存在λ=2，使得k1+k2=2k3成立．

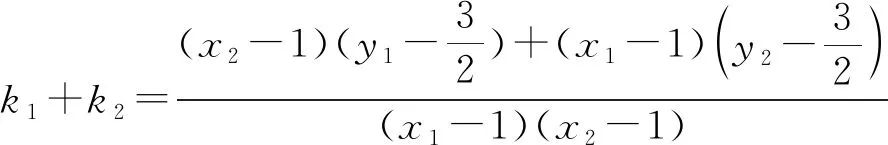
猜想1：既然常数“λ”的值与直线AB旋转无关，那可能只与直线AB过的定点——右焦点F有关．下面固定点F，让点P在直线x=1运动，结论是否依然成立？

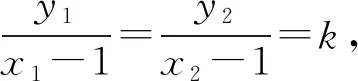
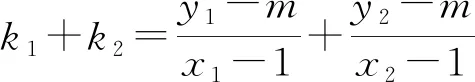
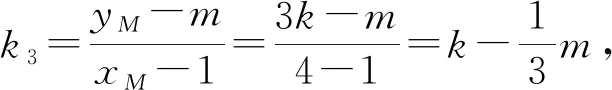
故存在λ=2，使得k1+k2=2k3成立．

从上面的证明过程来看，只要点P是直线x=1(过右焦点垂直于x轴)上的动点，就一定有k1+k2=2k3成立．

猜想2：观察直线l的方程x=4，不难发现它是椭圆的右准线，如果动点M在直线l上运动，直线MA，MB，MF的斜率间有没有什么确定的数量关系呢？

解：设M(4,n)，因为A，B，F三点共线，

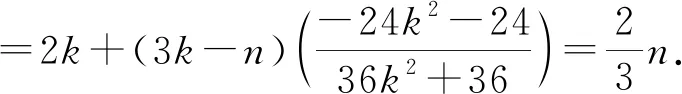
猜想3：从上面的三个问题可以发现，只要点F和直线l确定，这个常数是必然存在的．那么这个常数2与点F的坐标和直线l的方程之间有什么数量关系呢？因为点F是右焦点，直线l是右准线，它们之间存在一个对应关系．如果点F改成是椭圆长轴上的任意一点，是不是也存在这样的一条定直线l满足上面的关系呢？

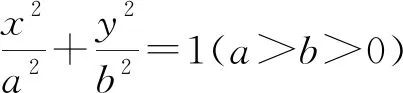
解：因为直线AB与直线l相交于点M，所以斜率存在，故可设直线AB的方程为：y=k(x-t)．设A(x1,y1)，B(x2,y2)，P(t,n)，

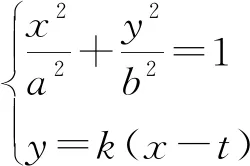
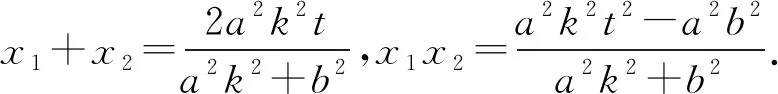
即M(m,k(m-t))．

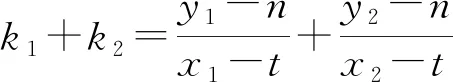
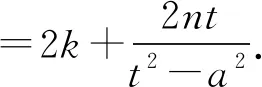
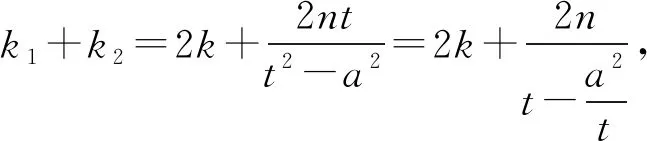
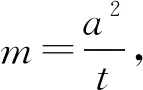
使得k1+k2=2k3成立．

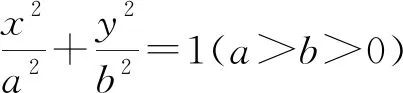
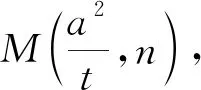
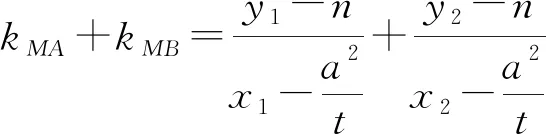
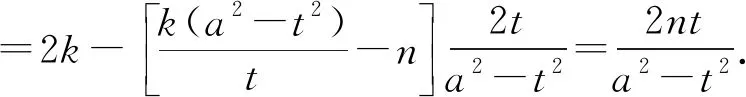
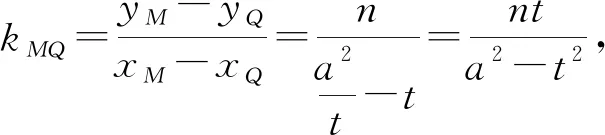
所以kMA+kMB=2kMQ．

背景链接：

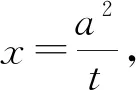
4 教后反思

“一题一课”最为突出的特点就是对数学“题”进行了深度挖掘，以“原题”为本，根据学生的认知规律作深思，设计出不同层次的探究题，由浅入深、浅显易懂，知识内容却深刻，思想方法显灵动．这是一节贴近学生最近发展区，突出学生自主探究过程的课堂教学．

4.1 了解学生学情，确定一个主题

4.2 遴选好的例题，衍生一串问题

瑞士数学家皮亚杰认为：学习过程并不是个体获得越来越多外部信息的过程，而是能动地建构新的认知图式，不断完整新的认知结构的过程．高三数学复习的教学目标是通过有限的复习，对所学知识获得螺旋式上升的认识，从而达到知识的系统化、网络化，使认知结构经过顺应和同化得到发展．如何通过少量题目的训练，而又要达到以上的理想目标，就离不开精心选择好的问题作为研究对象．本节课从寻找斜率之间的关系入手，在一个运动的过程中发现一个常数的存在，凸显了变中不变的本质，让学生产生去研究不变的常数如何刻画有规律的变化．基于以上的思考，产生了一个问题串，点P从一个定点变成一个动点，结果如何？右准线上的任意一点是否也有类似的规律？题中的定点F和右准线之间有着对应的关系，如果改变定点的位置，是否也存在对应的一条定直线，保持结论的稳定性呢？这一串问题很好地体现了“一题一课”选题的原则：层次性、开放性、广延性．问题的层次性让不同能力的学生在学力上得到不同的发展；问题的开放性让不同层次的学生都能参与；问题的广延性，易于学生发现问题做进一步的探究与推广．

4.3 强化类题训练，夯实一种方法

4.4 观察思考表达，促进深度学习

《普通高中数学课程标准(2017年版)》提出：“数学教育要引导学生学会用数学的眼光观察世界，培养数学抽象和数学建模素养；学会用数学的思维分析世界，培养逻辑推理和数据分析素养；学会用数学的语言表达世界，培养直观想象和数学运算素养．”高三数学复习要在发展核心素养的视角下设计专题复习，聚焦对问题的深度学习与思考，让学生在研究的状态下学习，而不是单纯的接受，而是在发现基础上的同化，重在引导学生通过亲身观察、深入思考、理性表达，达成对数学本质、思想、方法和价值的领悟，才能让学生真正学得明白，才能把发展数学核心素养落到实处．本节课从一个学生熟知的问题为观察起点，利用学生直观想象的能力，猜测其中可能存在某种结论，通过数学的思维去分析和论证变与不变的规律，学生的逻辑推理能力得到加强．在猜测和论证的过程中，不断调整和完善问题的条件和结论，得到一串正确的命题，学生数学抽象的素养得到锻炼．建构主义认为：“学习要放在活动中进行建构，只有在活动过程中不断地进行反省、概括和抽象，重构自己的理解，才能真正理解知识的本质．”