基于改进蚁群算法的仓储物流机器人路径规划*

辜 勇 段晶晶 苏宇霞 袁源乙

(武汉理工大学物流工程学院 武汉 430063)

0 引 言

现代物流业高速发展的过程中，智能仓储是其中的关键环节，用以保证物流过程能够对海量物料需求做出及时反馈，满足客户的需求.在仓储活动中，引入仓储物流机器人代替传统人工作业已成为必然趋势.亚马逊仓库，京东“亚洲一号”，海康威视等企业纷纷应用仓储物流机器人作业，显示了智能仓储的快速兴起和发展.其中仓储物流机器人路径规划是目前的热门研宄方向，在仓储物流[1]、工业生产[2]、分拣配送[3]等领域有着广泛的应用前景.移动机器人路径规划是指按照目标函数，避开所有障碍物，选择出一条从起点到终点的最优或次优的连续路径.其本质是在若干约束条件下得到最优解或可行解的问题.

常见的路径规划方法[4]有：人工势场法，模糊逻辑算法，神经网络法，智能优化算法等.Chen等[5]采用两阶段混沌优化方法，借助改进人工势场，有效克服了目标不可达的缺点，实现机器人路径规划.Noto等[6]在传统Dijkstra算法的基础上进行扩展，从初始点和目标点同时向外搜索移动机器人的最短路径，直到搜索结果重叠结束，以此加快收敛速度.王雷等[7]在遗传算法中加入人工势场对初始种群进行引导，克服基本遗传算法收敛速度慢等缺点.除此之外，蚁群算法常用于路径规划问题，是一种较为成熟和有效的智能化方法，具有随机并行搜索能力，许多学者对此展开大量研究.Qiang等[8]为避免机器人在早期的盲目搜索寻路，在蚁群算法中使用伪随机状态转移规则选择路径，并且引入动态惩罚方法解决死锁问题，有效提高了全局最优搜索能力和收敛速度.万晓凤等[9]在蚁群算法中利用挥发自适应方式更新信息素，有效避免陷入局部最优.王雷等[10]运用改进蚁群算法解决了机器人易陷入凹型障碍并在复杂环境搜索效率低的问题.杜磊等[11]在蚁群算法转移概率中引入自适应期望函数，通过增加相邻节点被选择概率的差距，避免路径迂回的出现.封声飞等[12]制定自适应的信息素更新策略，使蚁群算法在迭代后期仍具有较强的搜索能力.以上算法对路径寻优问题提出改进，针对的是不同类型的障碍物环境，对仓储环境下障碍物多变的情况没有普遍适用性.并且多数蚁群算法在搜索过程中易出现算法不稳定的问题.

此外，对于路径平滑处理方面，孙瑞等[13]提出控制点转移策略，通过控制路径走向的栅格中心点向栅格角顶点的转移，实现了路径规划的平滑改进.王红卫等[14]对A*算法规划的路径进行平滑优化，将两节点之间无障碍物的中间节点删除，建立平滑路径.上述算法侧重于转折角度大、折点多的路径平滑处理，且算法较为复杂.

本文在基本蚁群算法的基础上,提出一种改进蚁群算法.通过对蚁群的转移规则进行改进，随迭代次数动态改变信息素残留因子，使得移动机器人适应不同的障碍物环境变化；并对规划路径结果进行二次优化的处理.最后，通过仿真实验与其他算法对比，在不同复杂度的仓储环境下进行实验，结果验证了改进蚁群算法的有效性.

1 环境描述

常见的环境建模方法主要有可视图法、拓扑法、自由空间法,以及栅格法等.可视图法虽然能够得到最短路径，但将移动机器人视作质点，忽略尺寸大小，使得移动机器人在经过障碍物顶点时可能造成碰撞，且搜索时间较长.拓扑法利用拓扑特征大大缩小了搜索空间，但建立拓扑网络却十分复杂.自由空间法比较灵活，但其复杂程度与障碍物的多少成正比，并且有时无法获得最短路径.栅格法[15]从横、纵两个维度，将移动机器人工作环境分解成一系列的网格单元.将环境中的障碍物用栅格进行分割，不满一个栅格的按照一个计算.通过以栅格为单位记录环境信息，对有障碍物的地方进行区分，再利用路径寻优方法使移动机器人避开障碍物.

采用栅格化方法进行环境建模，见图1，在环境中建立直角坐标系，按照仓储物流机器人行走和转折时占用的最小空间，来切割横向和纵向区域.每个栅格都有确定的坐标(x,y)，x=row，y=col.其中:row为栅格所在的行号,col为栅格所在的列号.并用属性obstacle记录环境地图情况，当栅格被障碍物占据，如obstacle(20，1)=1；否则，obstacle(20，1)=0.

图1 环境建模

机器人在二维平面上的有限区域内工作，机器人在一个栅格上可以沿8个方向到达相邻的栅格，见图2.

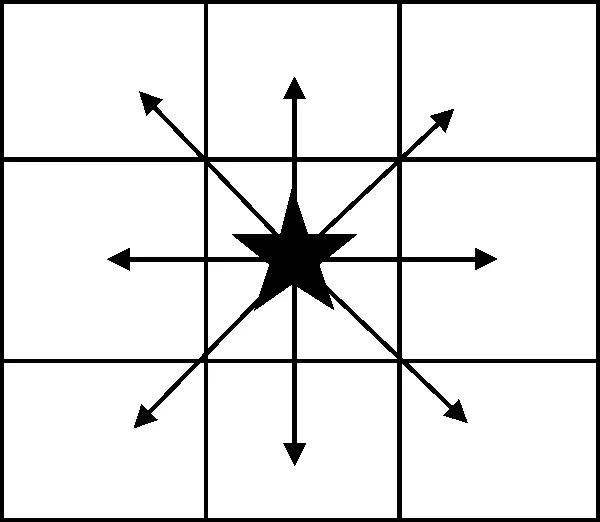
图2 机器人运动方向

2 基本蚁群算法

2.1 启发函数

蚁群算法是一种启发式算法，在选择下一个节点时，优先选择离自己最近的节点.定义人工蚁群的蚂蚁数目为m，当前节点i到节点j的距离为dij(i,j=1,2,…，n).两节点间的启发函数(或者可见度)为ηij，两节点间的信息素浓度为τij.则蚂蚁k从节点i转移至节点j的转移概率pkij.定义属性ηij为两节点间的启发函数(或者可见度)，是距离的倒数.

ηij=1/dij

(1)

dij=((ix-jx)2+(iy-jy)2)1/2

(2)

式中：dij为节点i和节点j之间的欧几里得距离；ix，iy为节点i的横纵坐标；jx，jy是节点j的横纵坐标.

2.2 信息素浓度

信息素浓度是蚂蚁群体协作发挥作用的关键.初始设置全局的信息素浓度均相等.随着不断探索和行走，蚂蚁在走过的路线上会留下与路径长度有关的信息素，引导后续蚂蚁选择优势路径.因此在全部蚂蚁完成一次循环后，对各路径上的信息素含量进行更新，更新规则为

τij(NC+1)=(1-ρ)τij(NC)+Δτij(NC)

(3)

(4)

式中：ρ为信息素挥发因子，ρ∈(0,1).Δτij(NC)第NC代中节点i到节点j之间路径上信息素增量.Δτkij(NC)为蚂蚁k本次迭代过程中在节点i和节点j之间的路径上留下的信息素含量.

2.3 转移概率

蚂蚁k从节点i转移到节点j的概率pkij为

(5)

式中：allowedk为蚂蚁k在该阶段可访问的节点集合；∂为信息素重要性因子，其值越大，表示蚂蚁越易选择有较多蚂蚁选择过的路径；β为启发函数重要性因子，其值越大，表示蚂蚁更易选择离自己最近的节点.

3 改进蚁群算法

3.1 转移概率

在栅格化环境下进行节点选择时，节点之间的路径长度已被标准化.

(6)

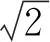
ηij=ζ/Lj

(7)

式中：Lj为节点j到终点之间的欧几里得距离；ζ为常数，通常节点距离终点距离较大，使得启发函数值ηij较小.因此可根据信息素因子τij的数量级，对启发函数进行扩大.

再者，引入变量q0，蚂蚁选择下一个节点S按式(8)的规则进行.

(8)

式中：q为随机变量，q∈(0,1).即在随机变量q小于变量q0时，蚂蚁选择转移概率最大的节点进行访问，否则，就随机选择节点进行访问.随着迭代的进行，q0的值先变大再变小，这使各蚂蚁在前期随机选择节点，有助于扩大全局搜索能力，寻找到优势路径；中期则选择概率最大的节点，及时收敛；后期又随机选择节点，有助于跳出局部最优.

3.2 信息素更新规则

信息素挥发因子ρ一般是常数，不利于蚁群算法在迭代过程中实现快速收敛与跳出局部最优之间的平衡.因此，在算法前期希望快速找到优势路径，需要一个较大ρ值；而在算法后期，为了避免陷入局部最优，需要扩大搜索范围，需要一个较小的ρ值，见图2.为此，ρ值随着迭代的进行，应该是一个由大到小的变化过程.可按照式(9)进行自适应变化.

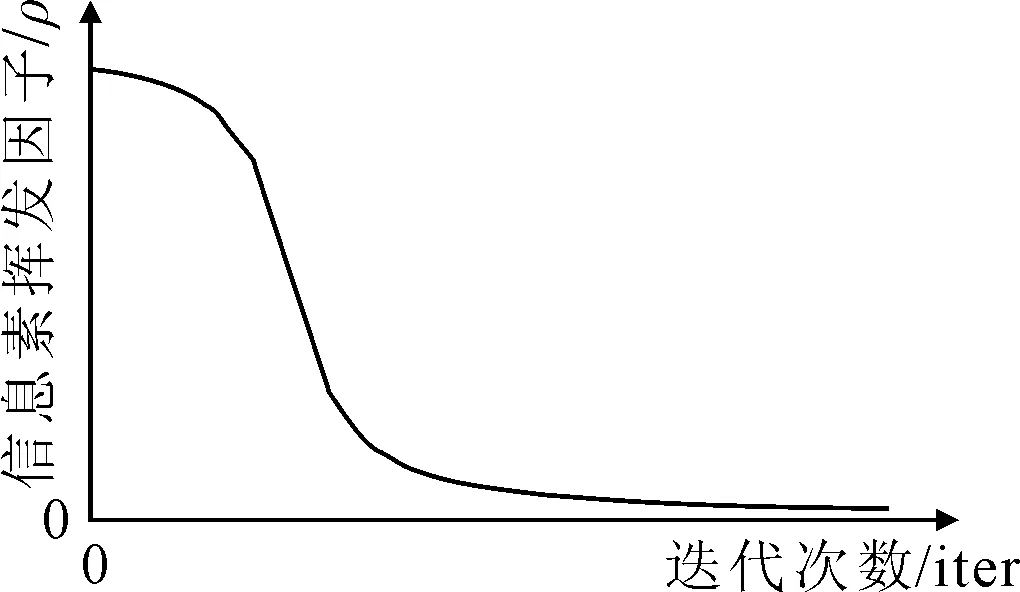
图3 ρ随迭代变化函数图

(9)

式中：c为常数，根据具体情况调整.

3.3 目标函数

仓储物流机器人路径规划的目的是能够找到一条从起点到终点的无障碍路径.假设机器人以匀速行走，那么路径最短的同时也能达到时间最短.因此，取路径规划的总长度L为目标函数,即

(10)

式中：dtij是在第t步从节点i到节点j的欧几里得距离.蚂蚁经历T步到达终点.

3.4 路径平滑

蚂蚁通过在栅格化环境中直线行走，在行走路径过程中，经过障碍物会有较多转折点.在实际工作环境下，移动机器人所得到的路径虽然总体上长度较短，但存在着个别不必要的折角，机器人在经过拐角时需要调整自身状态以适应角度转变，导致行驶难度加大，行驶时间增加.

为增加机器人行走路径的实际可行性，需要对改进蚁群算法规划出的路径进行平滑处理.假设改进蚁群算法的路径规划结果为Path，为二维数组[x(1),y(1);x(2),y(2);…；x(n),y(n)]；经过平滑处理后的结果为Smooth_Path，为二维数组[a(1),b(1);a(2),b(1);…；a(n),b(n)].平滑路径是通过使平滑前后路径偏离程度最小，见式(11)；同时路径的总转折角度较小，为

(11)

(12)

因此，路径平滑优化的目标函数为

(13)

式中：λ，μ为常数参数.通过调整λ和μ的值来找到最优化路径.

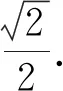
3.5 改进蚁群算法步骤

移动机器人路径规划包含环境的栅格法建模、改进蚁群算法进行路径规划、路径平滑处理等过程.具体流程描述见图4.

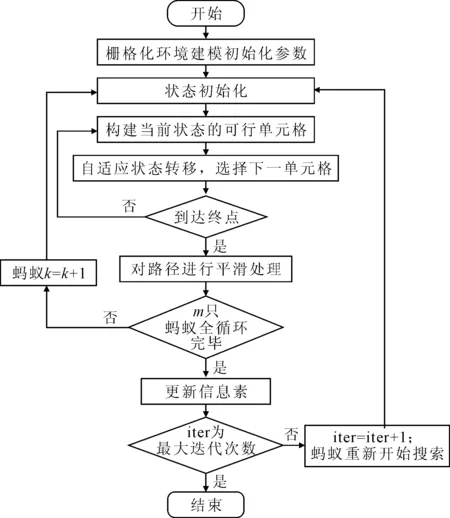
图4 算法步骤图

4 仿真实验

经过初步实验，改进蚁群算法的参数设置：NCmax为20；m为20；∂为1；β为7；Q为100；ζ为10；c为5；λ为0.5；μ为0.5.

转移概率中随机变量q0为

(14)

4.1 2020环境下算法比较

选取文献[12]的算例，该算例环境是较为规则的大型障碍物仓储环境.其运行结果与改进蚁群算法的行走路径对比，见图5a).其次，选取文献[9]的算例，该算例环境是零散分布的众多小型障碍物仓储环境.其运行结果与改进蚁群算法的行走路径对比，见图5b).

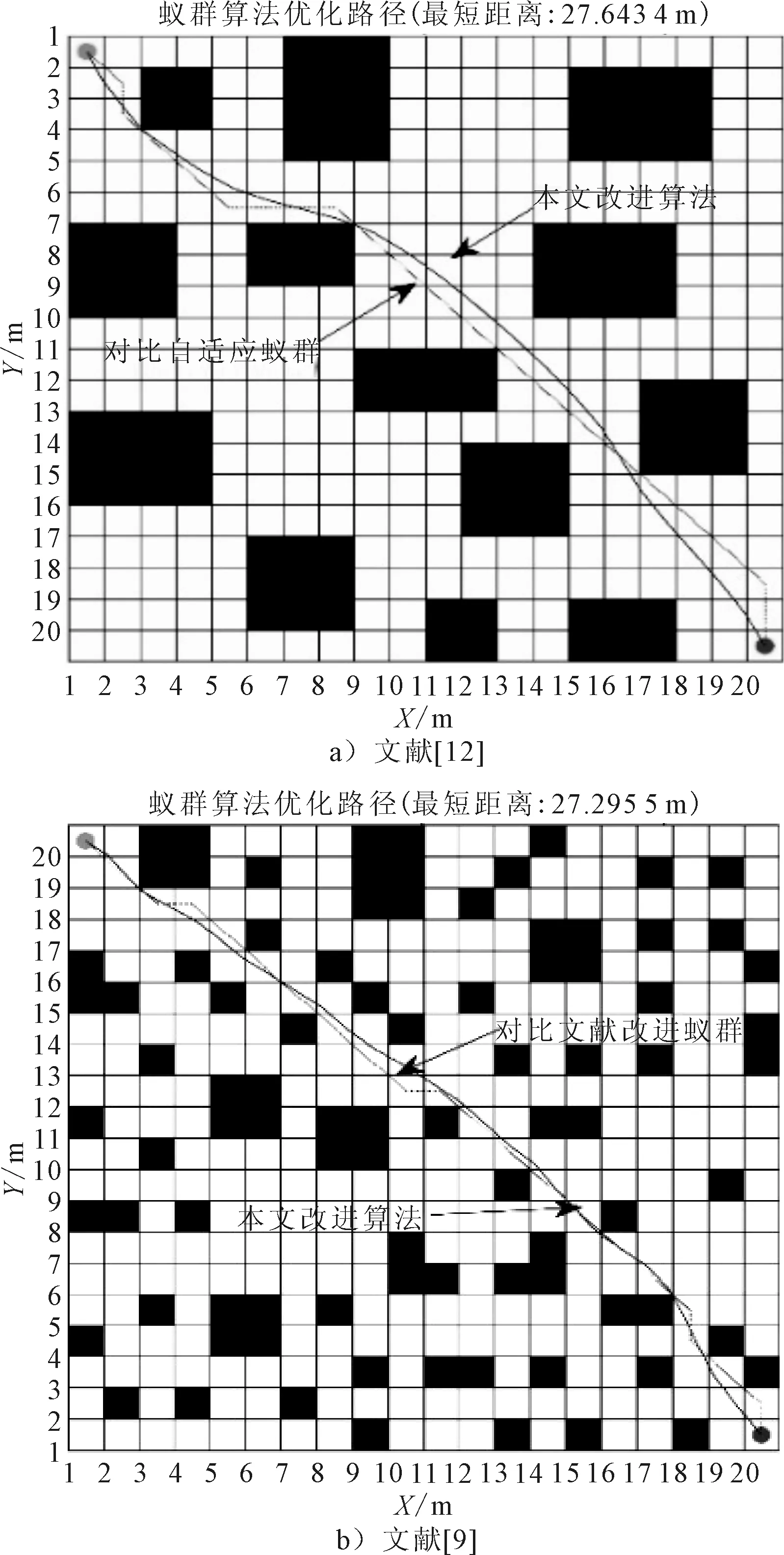
图5 文献[12]、[9]与改进蚁群算法对比

采用文献[12]的共同算例，算法均独立运行 20 次，比较仿真结果，两个算例的衡量尺度均为最优路径长度和收敛代数，见表1.由于路径的平滑处理，使得改进蚁群算法的最优路径长度在两种条件下，较文献[12]均有明显改进.并且转移概率中增大启发函数的作用，将随机性选择和确定性选择相结合，使收敛速度更快，更稳定.对比文献[12]，收敛代数平均值缩短一半，标准差减少16.4%；对比文献[9]，收敛代数平均值减少91.8%，收敛速度大幅增加.通过直观观察图4～5可知，改进蚁群算法路径更加平缓，转折角度更小.

4.2 30×30环境下算法比较

对复杂环境进行扩大，采用文献[7]的算例进行计算，对比结果见图6a).经过20次仿真，实验数据见表1.改进蚁群算法仍然具有较强优势.在最优路径方面，改进蚁群算法的最大值为43.571，小于文献[7]的最优路径平均值48.53，最优路径平均值要缩短10.2%；最优路径最小值、最大值和平均值均小于文献[12].与文献[12]对比，收敛速度更快、更稳定，见图6b).

4.3 障碍复杂程度不同的环境

为检验改进蚁群算法的普遍适应性.在20×20环境下利用MATLAB随机生成四组障碍物环境，障碍物比例分别是20%，25%，30%和35%，表示为环境1、2、3和4.平滑处理前后的算法运行结果对比，见图7.在30×30环境下障碍物比例是20%，表示为环境5，平滑处理前后的算法运行结果对比见图8.观察未平滑优化的路径规划结果，改进蚁群算法在障碍物占比不同的情况下，均能找到已知最优解；平滑优化之后，路径长度更短，减少了总转折角度.

为了进一步实验改进蚁群算法的效果，在五种环境下，分别对基本蚁群算法(ACO)和改进蚁群算法(IACO)在上述五种环境下，分别进行仿真实验，运行20次.对比结果见表2、表3.

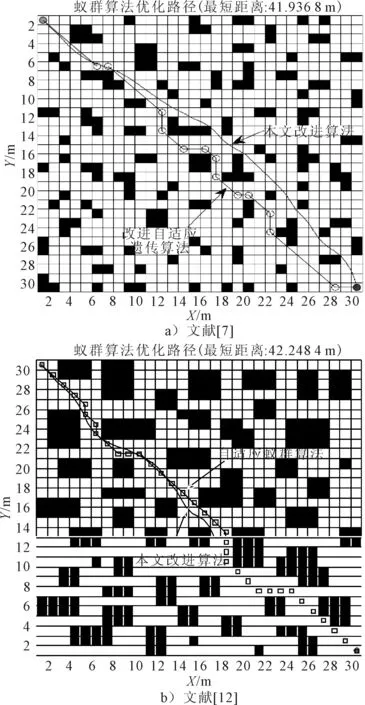
图6 文献[7]、[12]与本文算法对比

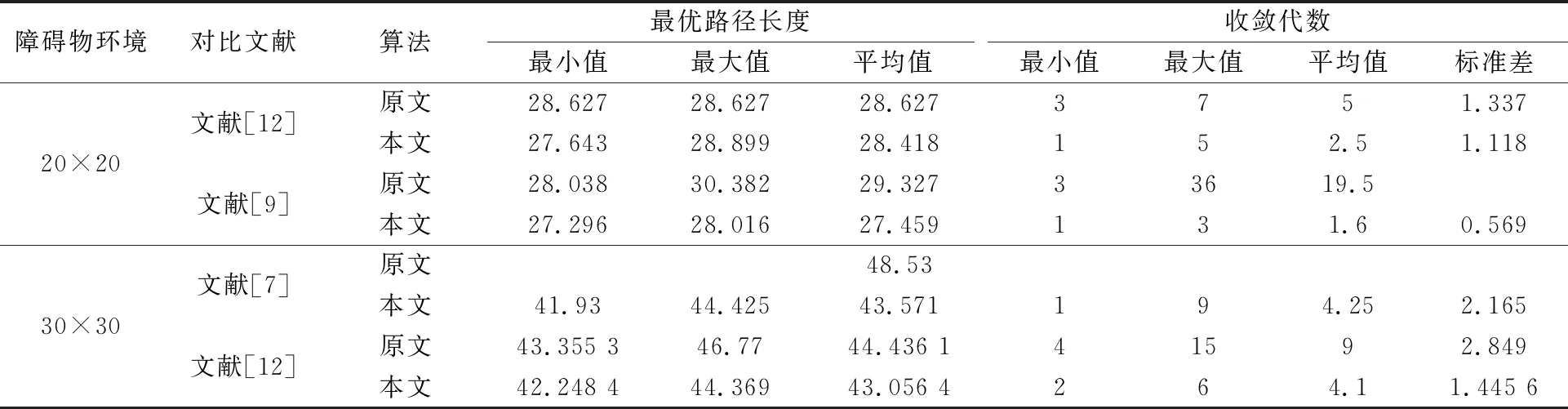
表1 文献[12]、[9]、[7]与本文仿真结果比较 m

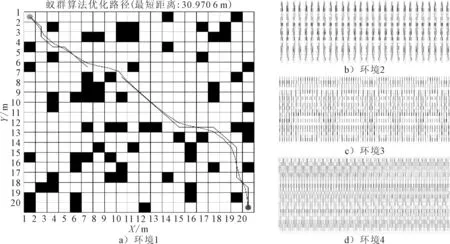
图7 20×20环境下不同复杂度路径寻优图

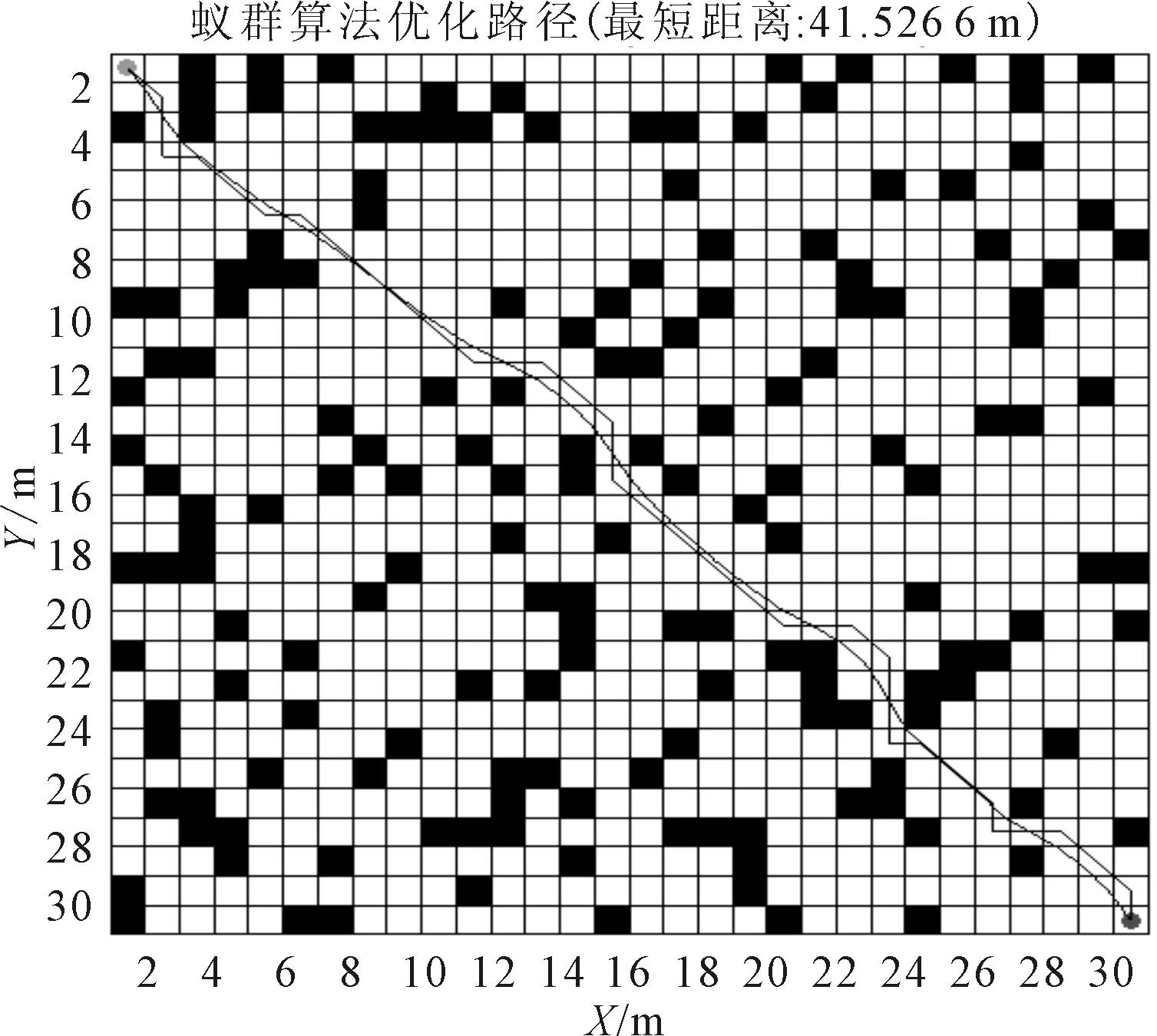
图8 30×30环境下路径寻优图(环境5)

表2 收敛所需的循环次数

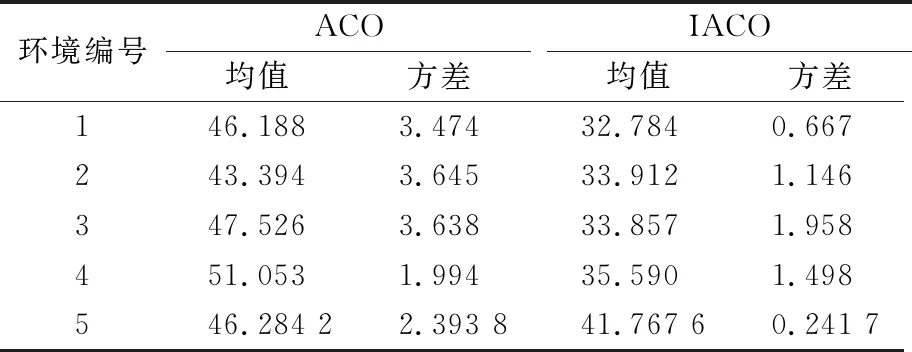
表3 最优收敛长度

由表2～3可知，改进蚁群算法运行效率高，收敛所需的迭代次数远低于基本蚁群算法；并且最优路径长度更短，结果更加稳定.改进蚁群算法扩大启发函数的影响力，使得算法初期就能够引导寻找到优势路径；转移概率采用确定性与随机性相结合的方式，有利于及时跳出局部障碍物，使得改进蚁群算法能够快速收敛至较优结果.

5 结 束 语

通过对仓储物流机器人路径规划问题进行栅格化建模，设计了一种新的求解机器人避障路径的改进蚁群算法.该算法改进路径选择参数，优化转移规则和信息素更新条件，并对路径结果进行平滑处理.随着算法迭代变化，对路径选择以及信息素挥发系数进行调整，在保证算法全局搜索最优的同时，能够快速收敛，并且有足够的稳定性.平滑处理后的路线更符合实际环境中机器人行走条件，减少能耗及缩短距离，也更加安全.