正定矩阵的性质及判定方法

何守元

(云南省丽江市丽江师范高等专科学校 674100)

先看正定矩阵的定义：若一个实二次型f(x1,x2,…,xn)=XTAX正定，则称矩阵A为正定矩阵.显然，由定义可知：正定矩阵A必须满足两个条件：首先，A必须是实对称矩阵.否则不存在正定矩阵的概念；其次，以A为矩阵的实二次型f(x1,x2,…,xn)=XTAX必须是正定二次型，即A与同价单位方阵E合同.

由此可得正定矩阵的一系列性质，它们是判定A为正定矩阵的依据：

性质1实对称矩阵A为正定矩阵的充要条件是A与同价单位方阵E合同. (因为A为正定矩阵的充要条件是实二次型f(x1,x2,…,xn)=XTAX是正定二次型.)

性质2正定矩阵的行列式大于零.(或：正定矩阵必满秩、可逆.)

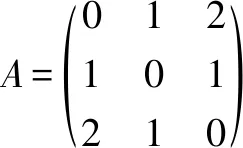
性质3正定矩阵的逆也是正定矩阵.

(因为A=PTEP,A-1=[(P-1)T]TE(P-1)T,A-1也与单位方阵E合同，必然正定.)

性质4实对称矩阵A为正定矩阵的充要条件是A的特征根全大于零.

这是因为：任意实二次型都可用正交变换化为标准型，标准型的矩阵的主对角元为它的特征根，必须全为正数.

性质5实对称矩阵A为正定矩阵的充要条件是A的顺序主子式全大于零.(这在一般教材上均有证明)

综合以上定义和性质，不难看出，正定矩阵具有下列显著特征：

(1)实对称矩阵(这是前提)；(2)满秩、可逆、行列式非零(这三个特征是等价的)；(3)与同阶单位方阵合同；(4)特征根全为正实数；(5)与同阶对角形方阵dig(t1,t2,…,tn)相似且合同(其中ti为它的特征根).(6)行列式等于t1t2…tn(即：全部特征根的积).

根据上述讨论，可得出正定矩阵的判别方法：

判法1若A为具体矩阵(元素全知)，则可直接计算它的顺序主子式，若全大于零，则A为正定矩阵.若不全大于零，则A非正定.

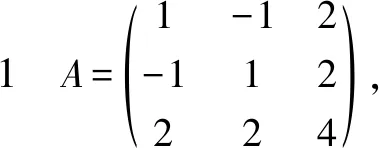
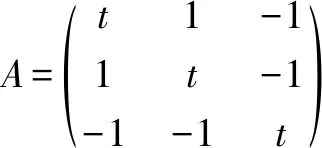
判法2若A为具体矩阵(元素全知)，则可直接解特征方程f(t)=|tI-A|=0，计算出A的全部特征根.若特征根全大于零，则A为正定矩阵.若特征根不全为正数，则A非正定.

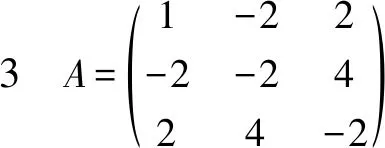
判法3若A为具体矩阵(元素全知)，则可用合同变换法，将其化为对角形矩阵.若对角形矩阵为单位方阵E(或：主对角元全为正数)，则A为正定矩阵.否则，不是正定矩阵.

如：上述例1中，对A施行合同变换：

得到的对角形矩阵不是单位方阵(或对角元出现负数)，故A不是正定矩阵.只有经合同变换后能变出单位方阵的实对称矩阵，才是正定矩阵.

判法4若A为具体矩阵(元素全知)，可直接计算A的行列式|A|，若|A|≤0，则A不正定.

这是根据性质2的等价命题来判定的.如：上述例1中，|A|=-16<0，说明A不是正定矩阵.注意：这是必要而不充分条件.行列式等于零的实对称矩阵当然不是正定矩阵，行列式大于零的实对称矩阵也不一定是正定矩阵.

对于抽象矩阵，可根据题目给出的具体条件，灵活应用正定矩阵的性质作出判断.如看n阶实对称矩阵的秩和正惯性指数是否都等于n？与它合同的矩阵是否为正定矩阵？由题中信息是否可推知其特征根全为正数？是否可推知其顺序主子式全大于零？等等.

例4若A是正定矩阵，E是与A同价的单位方阵，则k为足够大的实数时，可以判定kE+A也是正定矩阵.

事实上，若A的特征根为ti>0,则kE+A的特征根为ti+k，从而当k足够大时，就可保证kE+A的特征根全为正数，使kE+A为正定矩阵.

例5若A=(aij)是正定矩阵，bi(i=1,2,…,n)是任意n个非零实数，则B=(aijbibj)也是正定矩阵.

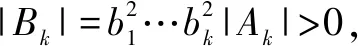
综上所述，深刻理解正定矩阵的定义和性质，就能在实际应用中对矩阵的正定性判别做到游刃有余，灵活自如！