城市峡谷中基于GPS 双极化天线的定位方法

王冠宇，孙 蕊，程 琦

（南京航空航天大学 民航学院，南京 211106）

0 引言

全球卫星导航系统（global navigation satellite system, GNSS），尤其是全球定位系统（global positioning system, GPS），在定位和授时方面得到了广泛的应用，对科学研究、经济建设和改善民生的诸多领域产生了深刻的影响[1]。然而，由于信号会被建筑物所阻挡或反射，GPS 在建筑密集的城市地区的定位精度不够可靠。GPS 信号接收类型分为视距信号（line-of-sight, LOS）、非视距接收信号（non-line-of-sight, NLOS）和多径干扰信号（multipath, MP）3 种。其中：LOS 指的是从卫星直接到达接收机的信号；NLOS 指经反射到达接收机的信号，且接收机没有收到视距信号；MP 指接收机同时接收到LOS 和NLOS 信号。NLOS 和 MP都会降低GPS 的定位精度，且造成的误差不能通过差分定位消除[2]，后文将这 2 种信号统称为MP/NLOS 信号。此外，NLOS 可能造成 100 m 左右的定位误差[3]。为此，国内外学者提出了多种方法来减少MP/NLOS 对导航定位的影响。

使用扼流圈天线[4]可以有效地减轻低高度角情况下的多径效应，但价格昂贵且笨重，目前主要用到大地测量领域。文献[5]改善相关器设计，缩小早迟相关器的间隔来减小多径误差；此后又出现了频闪相关器[6]和视觉器相关器[7]等。这些方法能在一定程度上降低 MP 造成的误差，但是对于NLOS 并不有效。

将卫星的观测值与其数据源结合，可有效减轻MP/NLOS 信号对定位精度的影响。GPS 与惯性导航系统（inertial navigation system, INS）的结合可以使2 种系统取长补短，从而弥补MP/NLOS 信号导致的精度下降[8]，但定位结果高度依赖INS 性能。GNSS与视觉传感器的结合也可降低多径误差，提高定位精度[9]，但易受天气等因素影响。依赖额外传感器，无疑会造成价格的提升。将3 维（3D）城市模型作为信息源，可以以较低的成本降低多径误差。使用3D 城市模型，可以检测进而排除掉 NLOS 的信号[10]，然而会导致可用卫星数减少。文献[11]提出了阴影匹配方法，先根据3D 城市模型预测信号接收类型，再与实际信号的接收类型进行比较，匹配程度最高的位置最可能是真实位置。文献[12]使用3D城市模型模拟信号传播路径从而计算模拟伪距值，再和伪距观测值比较，通过相似度来为候选点定权，从而采用加权平均的方法获得定位解。这些方法依赖对3D 城市模型的及时更新，对3D 模型的精度要求较高。此外对信号接收类型的准确判断也是此类方法的关键。只有准确地区分信号接收类型，才能得到较高的定位精度。

传统的信号接收类型区分方法是对载噪比（carrier to noise ratio, C/N0）划定阈值，C/N0较高的信号被分类成 LOS，C/N0较低的信号则被分类成 NLOS。文献[13]证明了在没有干扰的条件下，靠 C/N0值能得到可靠的分类结果，然而在实际情况下，由于天线位置变化、瞬间阻挡等原因，可能会出现LOS 信号表现为低C/N0值，而NLOS 信号表现为高 C/N0值的情况[13]。这种情况难以避免，因此仅依赖 C/N0是不够的，还需要引入更多的特征。卫星高度角也可作为分类指标之一。一般来说，高度角越低，信号是NLOS 的可能性越大；高度角越高，卫星被建筑挡住的可能就越小。文献[14]提出基于卫星高度角和几何精度因子的选星算法，分析了高度角对定位精度的影响。文献[15]在智能手机阴影匹配算法的研究中，也将 C/N0和卫星高度角结合分析，以判断LOS 的可能性。此外，越大的伪距残差意味着 NLOS/MP 的概率更大，因此对伪距残差进行一致性检验，也可检测MP/NLOS 信号[16-17]。使用双极化天线也可检测NLOS/MP 信号，GNSS 的直射信号表现为右旋圆极化（right-hand circularly polarized, RHCP），在建筑物反射后，入射角小于布鲁斯特角的信号变为左旋圆极化（left-hand circularly polarized, LHCP），其余保持RHCP[18]。双极化天线在1 个外壳中，将同轴 RHCP 敏感天线和 LHCP 敏感天线结合在一起，具有2 个输出：1 个是对RHCP 信号更敏感的常规输出，另1 个是对LHCP 信号更敏感的附加输出。经过反射后，总的接收信号将同时具有 LHCP 和RHCP 分量。受多径效应影响更严重的信号则具有更强的LHCP 分量。利用这个原理，文献[18]通过比较左、右旋圆极化天线输出的C/N0来检测NLOS信号[19]，若LHCP 天线的C/N0较大，则将该信号判断为NLOS。但由于天线的极化灵敏度随入射角的变化而变化，该方法在高度角较大的情况下效果较好，而对于低高度角信号效果较差[20]。因此仅凭 LHCP 和 RHCP 的 C/N0差值检测 NLOS 是不可取的，但LHCP 的C/N0可以作为分类特征。

机器学习可高速准确地处理多种类型特征，近年已被应用于提高 GNSS 定位精度。文献[21]将高度角和方位角作为支持向量机（support vector machine, SVM）的关键特征，以减轻静态定位的多径效应。文献[13]将C/N0、高度角等作为特征，用决策树区分 LOS 和 NLOS[13]。文献[22]提出了在车辆协作环境下，使用机器学习检测 NLOS 信号的方法。这些研究证明了机器学习是进行GPS 信号接收类型区分，提高定位精度的1 种有效工具。

MP/NLOS 信号会降低定位精度，因为2 者都会对伪距造成误差。通过修正伪距误差，或在定位过程中剔除受到影响的信号，都能够有效地提高定位精度。因此，针对上述方法的不足，本文提出基于双极化天线和梯度提升决策树（gradient boosting decision tree, GBDT）的GPS 信号接收类型分类方法和基于分类结果的定位方法。根据接收机的真实位置，计算每个卫星的伪距误差，并以RHCP 和LHCP 的信号强度、伪距残差、卫星高度角等测量值为特征，使用 GBDT 拟合伪距误差。然后利用 GBDT 预测的伪距误差的绝对值与阈值进行比较来对信号接收类型进行分类。此后对判断出的 MP/ NLOS 信号进行剔除或修正，用以提高定位精度。该方法不依赖INS 等昂贵的传感器，也不需要3D 城市模型，因而应能以较低的成本提高定位精度。

1 基于双极化天线和GBDT 的信号接收类型分类和定位方法

基于双极化天线和GBDT 的伪距修正和信号接收类型分类方法流程如图1 所示。

图1 算法流程

首先在已知位置使用双极化天线采集信号。对于每个卫星信号，分别采集其在RHCP 天线输出的载噪比和LHCP天线端输出的载噪比，与伪距残差η、卫星高度角θ数据组成历史训练数据集。根据真实位置计算每个信号的伪距误差，并用GBDT 算法进行拟合。此后可对测试集的伪距误差进行预测，将GBDT 预测的伪距误差的绝对值与阈值相比较，以对GPS 信号接收类型进行分类，此后将判断出的 MP/NLOS 信号进行剔除或修正，以进行更精确的定位。

1.1 伪距误差计算

卫星信号经反射到达接收机过程中，会经过额外的路程，导致NLOS 信号伪距增大，引起正的伪距误差。而 MP 信号是直射信号与反射信号的叠加，经相关器处理后，会出现正或负的伪距误差。2 者降低定位精度的原因都是伪距误差，因此本文将2 者归为一类，称为MP/NLOS 信号。接收机到某卫星之间的伪距ρ为：

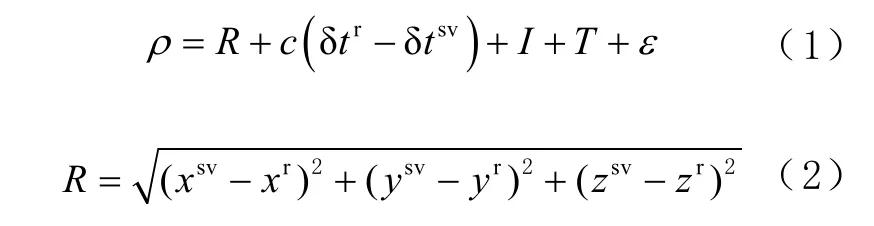
式中：R为卫星与接收机之间的几何距离分别为卫星和接收机在地心地固坐标系（Earth centered Earth fixed, ECEF）中的坐标；c为光速；分别为卫星和接收机的钟差；I和T分别为电离层和对流层的延迟；ε为包含了MP/NLOS、接收机噪声等造成的误差。这里考虑到噪声相对较小，可忽略不计，主要误差为MP/NLOS误差。卫星位置和卫星钟差修正值可由星历获得。已知接收机位置可计算卫星与接收机间几何距离，接收机钟差修正值也可通过解算伪距方程组获得。IK为Klobuchar 模型获得的电离，TS为Saastamoinen 模型获得的对流层延迟。因此，经过修正后的伪距ρc为：

伪距误差Δρ的计算式为

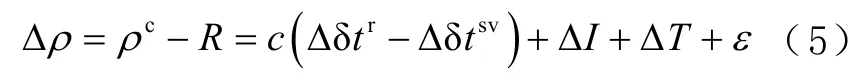
1.2 特征选取

在选择机器学习中输入的特征时，应同时考虑准确性和计算效率。尽管使用更多特征能在一定程度上提高准确性，但会降低计算效率。因此，仅使用以下4 个特征：

3）伪距残差η。伪距残差对信号接收类型分类具有很大的价值[23]。理论上，伪距残差的绝对值大小与 NLOS 的概率成正比，更大的伪距残差意味着NLOS 的概率更大；当采集的数据中，小部分信号是 NLOS 时，这种情况更突出[24]。文献[17]已证明，若有足够多的测量值，伪距残差可以作为1 个特征来检测MP 和NLOS 信号。

4）卫星高度角θ。一般来说，从高度角更高的卫星上发射出的信号更不容易被建筑遮挡，被建筑反射的可能更小，直线抵达接收机的可能性更大，越可能是LOS 信号。因此高度角可用作参考特征来减少多径效应对定位精度的影响。

1.3 基于GBDT 的伪距误差拟合

GBDT 是 1 种监督式机器学习算法[25], 它使用梯度提升思想将多个决策树结合起来。历史训练数据集中的每个样本表示为其中，为样本序号，N为样本数量。历史训练数据集可表示为T=其 中Δρi为每个样本的伪距误差。GBDT 每次迭代都沿着负梯度方向创建1 个弱学习器来减小损失函数的期望，其中a是决策树的参数，包括每个节点的分裂特征、最佳分割点、节点的预测值。本文中使用的损失函数为

设迭代次数为M，算法流程如下:

1）初始化弱学习器 f0（x）为

式中：f0（x）为仅含1 个根节点的决策树；γ为其输出。由于L为平方损失函数，f0（x） 为

① 计算负梯度为

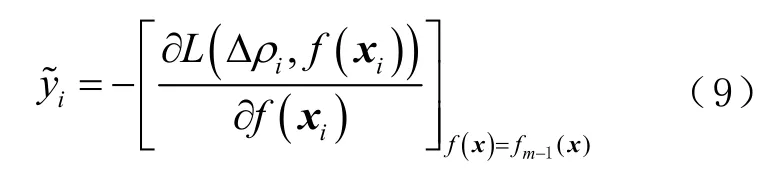
③更新强学习器为

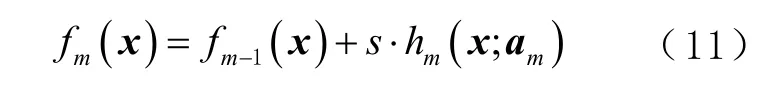
式中s是学习率，为防止过拟合，通常选在0～1 之间。

3）迭代结束后，输出fM（x）为最终的强学习器为

fM（x） 可以用来预测新样本的伪距误差。

1.4 定位方法

考虑到预测的伪距误差包括钟差、电离层和对流层延迟的残差项，即使LOS 信号也具有较小的伪距误差；因此设置阈值p以避免此类残差影响分类。伪距误差预测值的绝对值小于阈值的信号被分类为 LOS，反之则被分类为 MP/ NLOS。将MP/ NLOS 信号剔除后，可以提高定位精度。但由于剔除卫星信号会使卫星几何分布变差，可能会造成定位精度不提高反而变差的情况，因此设计了基于MP/NLOS 剔除与修正的定位方法，流程如图2 所示。该方法不会剔除所有 MP/NLOS 信号。对于每个MP/NLOS 信号，先判断将其剔除后对位置精度衰减因子（position dilution of precision,PDOP）的影响。若将其剔除不会导致PDOP 值增大，则会将其剔除；若剔除导致PDOP 增加，不剔除此信号，而是对其进行修正，即将该信号的伪距测量值减去伪距误差预测值。

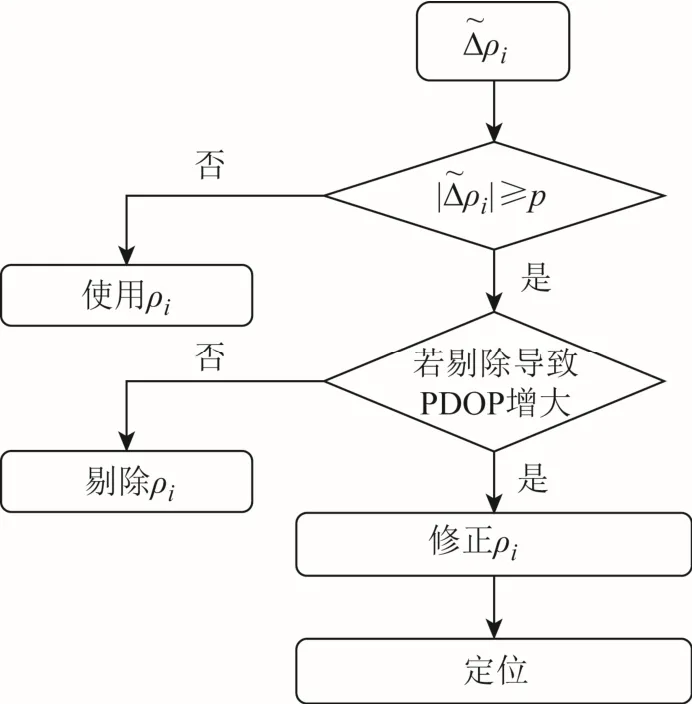
图2 基于MP/NLOS 剔除与修正的定位方法

2 实验与结果分析

为验证所提出的算法，笔者在中国台湾成功大学使用加拿大诺瓦泰公司的NovAtel Propak7 GPS接收机，以及浙江中裕通信技术有限公司的ZYACF-L004 型号的双极化天线，采集近7 h 的数据，计算每个信号的伪距误差。实验场景及所用双极化天线如图3 所示。

图3 实验场景及所用双极化天线

考虑到伪距误差包含式（5）中的各残差项，将阈值设为5 m，若数据集中伪距误差绝对值大于阈值，则分类为MP/NLOS 信号，反之则分类为LOS信号。抽取2 种样本各10 000 个生成训练集，将全部数据作为测试集和训练集，数据集样本数量如表1 所示。

表1 各数据集样本数量

本文使用GBDT 对历史训练数据集进行训练，并使用训练出的拟合规则对训练集和测试集的伪距误差进行预测，以测试算法。使用训练出的拟合规则对训练集本身进行的评估称为验证，利用测试集对算法进行的评估称为测试。本文将 GBDT算法与传统的线性拟合方法和二次多项式拟合方法[26]进行了比较。3 种方法拟合结果的均方根误差（root mean square error, RMSE）如表2 所示。从表2 可以看出，GBDT 算法的验证结果和测试结果的RMSE 均小于其他算法，这体现了GBDT 算法拟合伪距误差的优越性。

表2 各算法拟合精度比较

GBDT 算法分类准确性如表3 所示。

表3 信号接收类型分类准确性

表 3 中分类准确率表示的是正确预测的样本数量与数据集样本总数的比值（百分比）。每1 类的准确率指的是被正确分类为这 1 类的样本数与已知为这1 类的样本总数的比值（百分比），例如LOS 的分类准确率为，正确分类为LOS 的样本数与已知为LOS 的样本总数的比值（百分比）。验证和测试的总体分类准确率分别为 81.37 %和77.99 %，证明所提出的基于GBDT 的分类算法能够有效检测MP/NLOS 信号。

表4 比较了本文所提出的基于MP/NLOS 剔除与修正的定位方法与传统最小二乘定位解算的定位精度。

表4 定位精度比较

本文方法在各方向各维度上的定位精度均优于传统定位方法，其2D 和3D 定位的RMSE 分别为 17.94 和 31.69 m，相比传统定位方法提高了43.07 %和41.76 %，其2D 和3D 和 95 %分位点定位误差分别为36.86 和64.84 m，相比传统定位方法提高44.55 %和44.49 %。2 种方法的定位结果分别如图4 和图5 所示。本文提出的方法使得大部分定位解都分布在真实位置周围，远离真实位置的定位解数量明显少于传统定位方法。综上所述，所提出的算法能有效提高定位精度。

图4 传统方法定位结果

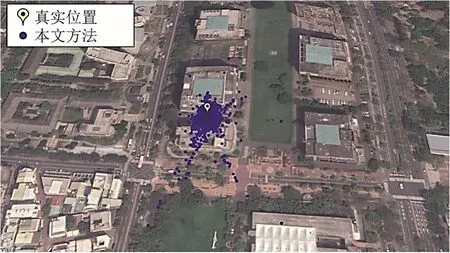
图5 本文方法定位结果

为了进一步验证所提出算法，将所提出的方法与传统定位方法的每个历元的定位结果进行了比较，如表5 所示。

表5 基于单个历元的定位精度影响分析

本文提出的方法提高了70 %左右的历元的定位精度；有14 %的历元的定位精度没有发生变化，这是因为在这些历元时可用卫星只有 4 颗，无法进行剔除或不存在，或未检测出 MP/NLOS 信号；由于 GBDT 存在误判，导致有少部分历元定位精度变差。总体来讲，本文所提出的方法对大部分历元的定位精度有提高效果。

3 结束语

随着导航定位技术的不断进步，人们越来越关注城市环境中的高精度定位。本文提出了1 种基于双极化天线的 GPS 信号接收类型分类算法，并将其判断出的MP/NLOS 信号进行剔除或修正，以提高城市环境中的定位精度。本文用双极化天线采集数据，将 RHCP 和 LHCP 天线输出的载噪比以及卫星高度角、伪距残差作为特征，使用GBDT 算法对伪距误差进行拟合。训练出的拟合规则可用于预测伪距误差，将其绝对值与阈值进行比较，以对 GPS 信号接收类型进行分类，此后将判断出的MP/NLOS 信号进行剔除或修正，以进行更精确的定位。实验证明，所提出方法能够提高大部分历元的定位精度，其2D 和 3D 定位的 RMSE 分别为 17.94 和 31.69 m，相比传统定位方法提高了43.07 %和41.76 %。此外，本文所提出定位方法的95 %分位点定位误差相比传统定位方法也有显著提高。本文所提出的算法不需要高精度惯导等昂贵的传感器，也不需要3D 城市模型等额外的信息源，且输入特征较少，因此能以较低的成本、较高的计算速率来提高城市中的定位精度。由于所用特征较少，在提高计算速率的同时，算法对环境变化较敏感。在未来的研究中会使用更多的特征，并且进行动态的定位实验。